corso analisi dei dati

1) ANALISI DI UNA SOLA VARIABILE
CREAZIONE DI UNA DISTRIBUZIONE DI FREQUENZA
proc freq data= libref.filename;
tables variable;
run;
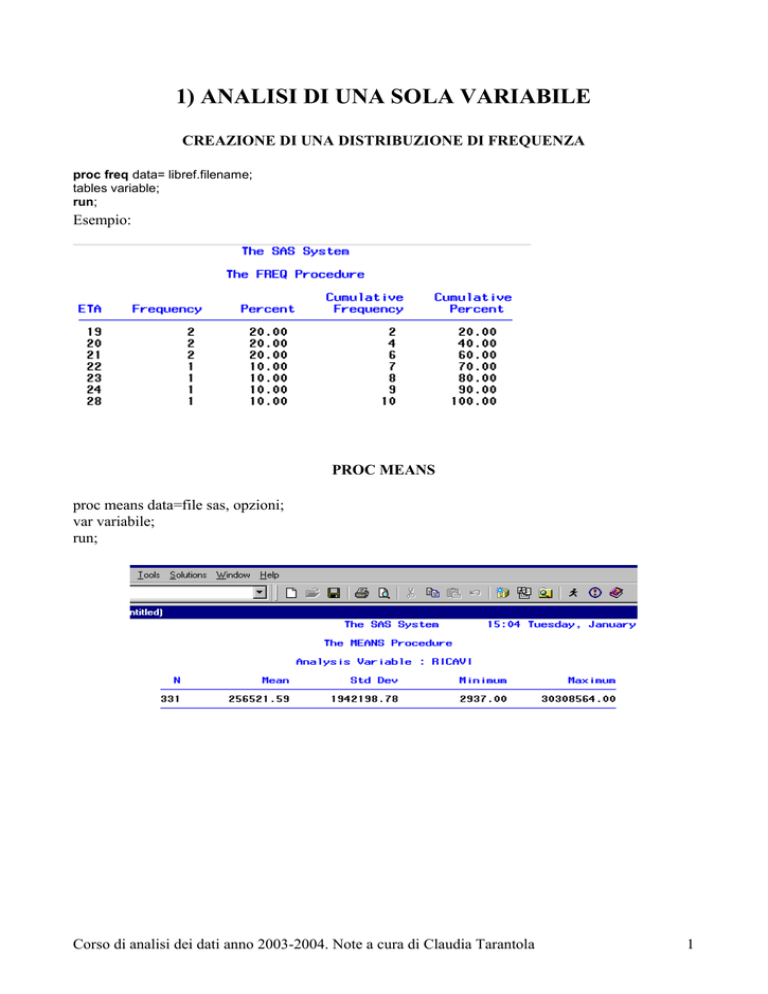
Esempio:
PROC MEANS
proc means data=file sas, opzioni;
var variabile;
run;
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
1
PROC UNIVARIATE
proc univariate data=file sas;
var variabile;
run;
Indice di asimmetria (Skewness)

 1  33 dove  3 

 x
 
3
i
.
N
Se la distribuzione è simmetrica = 0.
Si dice inoltre che una variabile presenta:
1) asimmetria negativa se <0;
2) asimmetria positiva se>0.
Indice di curtosi

  xi    .
 2  44 dove  4 
N

4
Si noti che 2 > 0. In particolare:
1) se la variabile è normale = 3;
2) Se < 3 la distribuzione è detta iponormale (cioè rispetto alla distribuzione normale ha densità
di frequenza minore per valori molto distanti dalla media);
3) Se > 3 la distribuzione è detta ipernormale (cioè rispetto alla distribuzione normale ha densità
di frequenza maggiore per valori molto distanti dalla media).
Osserviamo che in SAS® l’indice di curtosi corrisponde a -3. Valgono quindi tutte le
considerazioni precedenti con le dovute modifiche.
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
2
RAPPRESENTAZIONI GRAFICHE
proc gchart data=libref.filename;
type of graph variable;
run;
quit;
Per variabili discrete usare l’opzione \discrete
Tipologie di grafici
Vbar
Hbar
Pie
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
Donut
3
Creazione di un istogramma con SAS insight
Analyze-histograms: l’altezza di ogni barra corrisponde ad una frequenza (non corretto)Analyzedistribution: l’altezza di ogni barra corrisponde ad una densità di frequenza.
No
Sì
Boxplot
massimo
terzo quartile
mediana
primo quartile
minimo
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
4
2) DUE O PIÙ VARIABILI
TABELLE A DOPPIA ENTRATA
proc freq data=libref.filename;
tables variable1*variable2;
run;
SCATTER PLOT
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
5
INDICE DI CONNESSIONE
h
k
Chi-square: X  N 
2
p
XY
( xi *, y j *)  p X ( xi *) p y ( y j *)
p X ( xi *) pY ( y j *)
i 1 j 1

2
.
Indice  (Phi):

~
Indice di Cramer:  

min k  1, h  1
X2
.
N
.
proc freq data=file sas;
tables variabile1*variabile2/chisq;
run;
MATRICE DI VARIANZA E COVARIANZA
proc corr data=file sas cov;
var lista delle variabili;
run;
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
6
MATRICE DI CORRELAZIONE
proc corr data=file sas;
var lista delle variabili;
run;
REGRESSIONE LINEARE
proc reg data=file sas;
model var.risposta=var.esplicativa;
run;
Composite= 9320.46465+1.80209 Computer.
Corso di analisi dei dati anno 2003-2004. Note a cura di Claudia Tarantola
7