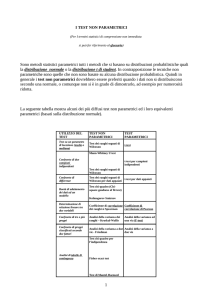
Test non parametrici
Il test T di Student per uno o per due campioni, il test F di Fisher per
l'analisi della varianza, la correlazione, la regressione, insieme ad altri test
di statistica multivariata sono parte dei metodi di inferenza classici o
metodi di statistica parametrica.
Prima della loro applicazione, è fondamentale che siano soddisfatti alcuni
assunti che riguardano la popolazione d'origine;
Primo assunto: l'indipendenza dei gruppi campionari
i campioni sottoposti ai differenti trattamenti dovrebbe essere formati per
estrazione casuale da una popolazione, in cui ogni soggetto abbia la stessa
probabilità di essere incluso in un gruppo qualsiasi. In questo modo, i
fattori aleatori o non controllati, quelli che nel test t formano l’errore
standard, sarebbero distribuiti casualmente.
Secondo assunto: normalità delle distribuzioni
da essa deriva,per via del teorema del limite centrale, una stretta relazione
tra popolazione e campioni.
Terzo assunto: omoschedasticità o omogeneità delle varianze.
Quando questi assunti non sono rispettati si ricorre ai c. d. metodi
statistici non parametrici, i quali non dipendono dalla forma di
distribuzione della popolazione, non si basano sui parametri della
distribuzione ed è possibile applicarli anche nei casi di dati qualitativi.
Vi sono diversi metodi, o tests non parametrici e si dividono in due
grandi categorie: quelli basati sulle frequenze e quelli basati
sull'ordinamento delle informazioni. I metodi non parametrici sono meno
efficaci ma più generali e vengono utilizzati quando non possono essere
applicati i metodi parametrici.
TEST χ² (Chi-quadro).
Quando si dispone di un solo campione spesso si ricorre alla verifica di
accordo della distribuzione osservata con una distribuzione teorica o
attesa. Per questo scopo si usa il test della χ², uno dei più diffusi test non
parametrici. Esso è basato sulle frequenze, noto come bontà d'adattamento.
Si tratta di confrontare le frequenze empiriche con quelle teoriche
(probabilità a-priore) per stabilire se la funzione di distribuzione di una
v.c. è quella da noi ipotizzata. Sotto l'ipotesi nulla H0 : ni nˆ i , cioè che le
frequenze empiriche sono uguali a quelle teoriche n̂i (probabilità attesa), si
calcola la statistica g c
2
(ni nˆi ) 2
i
e se
nˆi
2
H0 , mentre si rifiuta l'ipotesi nulla se c
2
>
c2
<
2
non si rifiuta
con probabilità pari a α
(g sono i g.d.l., g k v 1 ).
Esempio 1).
Adattamento di una distribuzione di Poisson alla distribuzione del numero
di incidenti in 120 settimane, con α = 0.05.
n. inc.
settimane
0
23
1
48
2
27
P( x)
H0 : X~> Poisson
la media è λ = 1.5
n.
inc.
0
1
2
3
4
5
Pi
N x Pi
23
48
27
13
6
3
0.2231
0.3347
0.251
0.1255
0.0471
0.0141
26.776
40.163
30.123
15.061
5.648
1.6944
Poiché
4
6
5
3
x exp( )
x!
1.5 x exp( 1.5)
quindi P( x)
x!
ni
120
3
13
CHI-q
27
40
30
15
6
2
27
40
30
15
8
0.593
1.6
0.3
0.267
0.125
2.884
c2 = 2.884 < 3 02.05 = 7.814725
gdl
5-1-1=3
2
7.814725
3 0.05
si accetta H0
Esempio 2).
Normalità della pressione sistolica in un campione di 1000 persone.
con α = 0.05.
Si stimano la media e la varianza dal campione.
H0 : X~> N(μ,σ²)
x
1
n
xi f i = 145.6
1
Sˆ 2
n 1
(x
i
x ) 2 = 702.3
freq.
classi
soggetti Z1
Z2
Prob teoriche Chi-Q
0
100
32 -5.49 -1.72 0.04
43
2.8140 media
100
120
124 -1.72 -0.97 0.12
124
0 var
120
140
260 -0.97 -0.21 0.25
249
0.4859 dev st.
140
160
340 -0.21 0.543 0.29
290
8.6207
160
180
139 0.54 1.298
0.2
196 16.5765
180
200
85
1.3 2.053 0.08
77
0.8312
200 oltre 200
20 2.05 5.826 0.02
20
0
gdl
2
1000
29.3283 4 0.01
13.277
02.05
9.488
P-val 6.70E-06 4
Il valore della
rifiuta H0 .
145.6
702.3
26.5
4
c2 è superiore al valore teorico della Chi-quadro, quindi si
Metodi non parametrici con ordinamento delle informazioni.
Questi metodi non parametrici sono test statistici basati sui ranghi delle
osservazioni, cioè sul loro numero d'ordine invece che sulle osservazioni
in se. Essi prescindono dalla distribuzione della popolazione (infatti si
usano quando non è possibile conoscerla).
Rispetto alle stime sono meno efficienti di quelli parametrici.
Sono giustificati quando:
1) le variabili hanno evidenti scostamenti dalla normalità (o sono
fortemente asimmetriche o presentano più di un picco);
2) quando il campione è troppo piccolo per comprendere se esiste una
distribuzione normale dei dati;
3) quando le osservazioni sono rappresentate da classifiche ordinali (es.
gravità di una malattia da 1 a 4).
Test di Mann-Whitney (o della somma dei ranghi): due campioni
indipendenti; è uno dei test non parametrici più potenti e serve a verificare
se due gruppi indipendenti appartengono alla stessa popolazione. È
un'alternativa molto valida al test parametrico T-Student, quando non
possono considerarsi i postulati del T test, oppure la scala di misura è più
debole di una scala ad intervalli.
Es. diuresi in due gruppi di soggetti sottoposti a due
trattamenti (3 con placebo e 4 con farmaco)
Placebo
Farmaco
Diuresi
Rango
Diuresi
Rango
1000
1
1400
6
1300
5
1600
7
1200
3
1180
2
1220
4
Test di Verifica:
Ipotesi Ho :me(1) = me(2)
U min R1 , R2
j
i
u
n1 (n1 n2 1)
2
u
n1n2 (n1 n2 1)
12
Z=
U u 0 .5
u
(+0.5 coda a sx; –0.5 coda a dx)
n1 (n1 1)
R
2
Nel caso di piccoli campioni, una volta calcolato la somma dei ranghi si
confronta questa con il valore teorico di una tavola in corrispondenza delle
dimensioni dei due campioni. Per grandi campioni si usa Z = N(0,1).
Oppure: U = n1n2
Es.: un gruppo di comunità con un certo comportamento e un altro gruppo
di controllo sono sottoposti ad un test i cui risultati sono espressi in
punteggi: g1) gruppo di controllo, g2) gruppo di comunità. Test
unidirezionale a sinistra: ipotesi: H0:me(1) = me(2) contro H1 :me(1) <
me(2).
g1 g2 C ord. dati rang
N1 N2 R
13 10 1 1 6 1.5
16 23 200
12 10 2 2 6 1.5
Test
12 10 1 3 7
5 MANN-WHITNEY
mu
320
10 8 1 4 7
5
U= 304
var
1226.667
10 8 1 5 7
5
sigma 35.0238
10 6 1 6 7
5
alfa= 0.05
10 17 1 7 7
5 Tavole di U(16,23)= 253
U=
-3.4119
9 16 1 8 8 9.5 304 > 253, quindi si
P-value 0.000323
8 15 1 9 8 9.5 rifiuta Ho, I due
Z critico -1.645
8
7
7
7
7
7
6
15 2
15 2
14 1
14 1
14 1
13 1
13 1
13 2
10
11
12
13
14
15
16
17
gruppi differiscono
8 9.5 signif.
8
9
10
10
10
10
10
9.5
12
16
16
16
16
16
12 2
12 2
12 2
12 2
11 1
11 1
2
2
2
2
1
2
2
2
2
2
2
2
2
2
2
2
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
10 16
10 16
11 20.5
11 20.5
12 24.5
12 24.5
12 24.5
12 24.5
12 24.5
12 24.5
13 29.5
13 29.5
13 29.5
13 29.5
14 33
14 33
14 33
15 36
15 36
15 36
16 38
17 39
Test della Mediana
Consiste nel costruire una tabella di contingenza 2x2 dove sono riportati i
valori dei due campioni distinti maggiori del valore mediano dell'insieme
dei due campioni e i valori minori o uguali al valore mediano.
gruppo 1 gruppo 2
maggiore della mediana
A
B
min. e uguale alla mediana
C
D
m
n
A+B
C+D
N
Calcolare poi la statistica χ² per tabelle 2x2 con 1 gdl:
2
N ( AD BC N / 2) 2
( A B)(C D)( m)( n)
L'potesi è Ho :me(1) = me(2). Il test si può usare quando i valori nei due
gruppi sono misurati almeno su una scala ordinale.
Applicazione all'esempio precedente dove la mediana comune è 11 e
α = 0.05 .
> mediana
<=mediana
g1
3
13
16
g2
15
8
23
18
21
39
coeffi. Xq P-value
6.435 0.0111
Poiché il valore χ² è 6.435 > 3.841 (valore teorico Chi-q) si rifiuta H0 .
Test di Wilcoxon (o test del segno per ranghi): campioni dipendenti
o dati appaiati; è l'equivalente del paired T test . Questo test è molto utile
nel campo delle scienze comportamentali. Consente di considerare la
direzione e la grandezza della differenza dei dati appaiati (mentre il test dei
segni considera solo la direzione delle differenze delle coppie dei dati).
Test di verifica:
Ipotesi Ho :me(1) = me(2)
T+ = ΣR+
T
T
n1 (n1 1)
4
n1 (n1 1)(2n1 1)
24
d T T
Z=
T T
T
Nel caso di piccoli campioni (n<20) si ricorre a delle tavole dove ai valori
di T+ sono associate delle probabilità P(T+ ≥ c) in base a n; per accettare
Ho la condizione è che P > α; si può ricorrere anche a questa statistica:
W
T
R
2
e se il P-value ad essa associato è minore di α si rifiuta Ho.
Per campioni grandi (n>20) si usa Z =
T T
T
e si accetta Ho se
Z Z (oppure Z < Zα e Z > -Zα ).
Esempio: stimoli visivi nell'interpretazione di segnali uditivi (congruenza
tra movimenti delle labbra e suoni delle parole).
Esperimento in condizioni di normale conversazione con 12 bambini da 10
a 16 settimane.
Quantità di tempo durante la quale ogni bambino guarda il viso di una
persona che parla in sincronia e fuori sincronia.
Ipotesi nulla H0 : la quantità di tempo che il bambino trascorre a guardare
non dipende dalla presentazione; in termini di test di Wicoxon non c'è
differenza tra mediana dei ranghi positivi e mediana ranghi negativi (per
piccoli campioni non c'è differenza tra la somma dei ranghi positivi e la
somma dei ranghi negativi ).
Test a due code (la direzione delle differenze non è nota in anticipo) con
α = 0.01 e 0.05; la regione critica consiste in tutti i valori di T (somma dei
ranghi positivi) elevati con una probabilità inferiore ad α = 0.01 e 0.05.
Il tempo misurato consiste in percentuali di disattenzione alla
presentazione in o fuori sincronia.
diff
rank (rank
segno
segno
(rank
sogg. sincrone asincrone As-S diff
diff)^2 rank
rank
diff)^2
1
20.3
50.4 30.1
9
81
9 Somme
73
650
2
17
87
70
11
121
11
3
6.5
2501 2494.5
12
144
12
Wilcoxon 2.8633
4
25
28.5
3.5
3
9
3
P-value 0.0042
5
5.4
26.9 21.5
7
49
7 alfa=0.01 Z critico 2.576
6
29.2
36.6
7.4
5
25
5 alfa=0.05 Z critico 1.960
7
2.9
1
-1.9
1
1
-1
8
6.6
43.8 37.2
10
100
10
9
15.8
44.2 28.4
8
64
8
10
8.3
10.4
2.1
2
4
2
11
34
29.9
-4.1
4
16
-4
12
8
27.7 19.7
6
36
6
Sia la tavola della somma ranghi che la statistica Z portano al rifiuto di H0
(con n = 12, P(T+ ≥ 73) = 0.0024, al valore di T=73 corrisponde una prob.
2x0.0024 e Z=2.8633 > di Z(α)=2.576). I bambini sono in grado di
discriminare le parole dai movimenti delle labbra in sincronia e fuori
sincronia.
Test dei segni.
Es. effetto di un diuretico su 6 soggetti:
Sogg. DiuresiP DiuresiD Diff. Rango diff. Rango con segno
1
1600 1490 -110
5
-5
2
1850 1300 -550
6
-6
3
1300 1400 +100
4
+4
4
1500 1410
-90
3
-3
5
1400 1350
-50
2
-2
6
1550 1520
-30
1
-1
(N.B. : i ranghi sono attribuiti sulla base del valore assoluto)
sogg.
A
1
2
3
4
5
6
B
1600
1850
1300
1500
1400
1550
rank
diff B-A diff
1490
-110
1300
-550
1400
100
1410
-90
1350
-50
1520
-30
(rank
segno
(rank
diff)^2 segno rank
rank
diff)^2
5
25 -5
Somme
-13
91
6
36 -6
4
16 4
Wilcoxon -1.36277
3
9 -3
P-value 0.172955
2
4 -2
Z critico
1.960
1
1 -1
Test di Wilcoxon applicato ad un solo campione.
In questo caso il test non parametrico sostituisce il calcolo dell'intervallo di
confidenza sulla media quando non è possibile ricorrere ai metodi
parametrici perché mancano le condizioni (non è rispettata la normalità
della distribuzione, ecc.). L'ipotesi sul valor medio viene verificata
prendendo come riferimento la mediana. Stabilita la mediana (ipotesi
nulla), si fanno le differenze dei valori dalla mediana e i ranghi delle
differenze in valore assoluto. Si sommano poi i ranghi di segno positivo.
Es.: 13 osservazioni, Ho: mediana=300, H1: mediana < 300, α = 0.05
oss
235
230
180
250
280
330
440
430
260
225
240
255
215
diff(Ho)
-65
-70
-120
-50
-20
30
140
130
-40
-75
-60
-45
-85
ranghi
65
70
120
50
20
30
140
130
40
75
60
45
85
7
8
11
5
1
2
13
12
3
9
6
4
10
13
-7
-8
-11
-5
-1
2
13
12
-3 media
45.5
-9 sigma 14.30909
-6 Zc
-1.29288
-4
0.098026
-10 Z critico -1.64485
27 T+
Dalle tavole, con n = 13, P(T+ ≤ 27) > α (T+ può essere al massimo 21.7),
quindi si accetta Ho.
In condizioni di incertezza sull’esistenza delle condizioni richieste da un test parametrico, una
soluzione sempre più diffusa suggerisce una duplice strategia:
1 - utilizzare un test appropriato di statistica parametrica,
2 - convalidare tali risultati mediante l’applicazione di un equivalente test non parametrico.
Se le probabilità stimate con i due differenti metodi risultassero simili, sono confermate la
robustezza del test parametrico e la sua sostanziale validità anche in quel caso. Il test non
parametrico può servire per confermare i risultati ottenuti con quello parametrico. Se le probabilità
risultassero sensibilmente differenti, dovrebbe essere considerato come più attendibile il test non
parametrico e sarebbe conveniente riportare nella pubblicazione solo esso, in quanto fondato su
condizioni meno rigorose e caratterizzato da inferenze più generali.