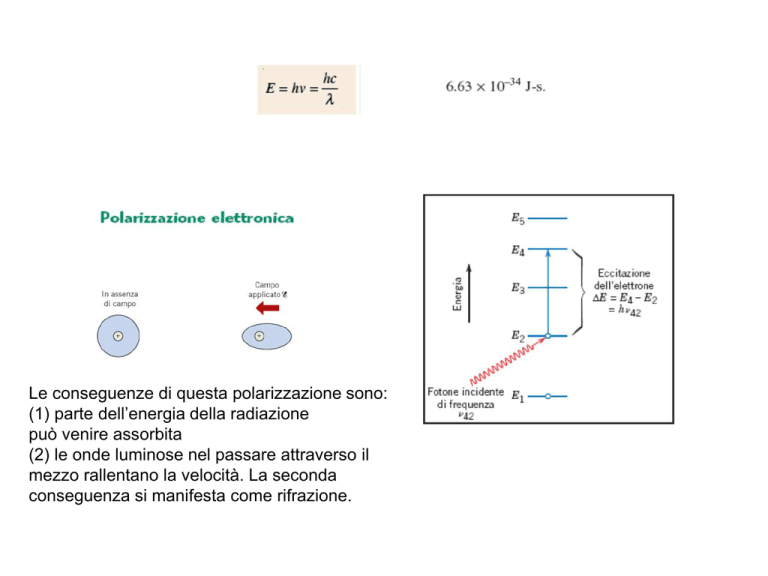
Le conseguenze di questa polarizzazione sono:
(1) parte dell’energia della radiazione
può venire assorbita
(2) le onde luminose nel passare attraverso il
mezzo rallentano la velocità. La seconda
conseguenza si manifesta come rifrazione.
Forza
L’Oscillatore Forzato:
Lo sfasamento tra
l’oscillatore e la forza
dipende dalla frequenza.
Siano w0 la frequenza
dell’oscillatore, e w quella della
forza.
Oscillator
e
Sotto la
risonanza
w << w0
Debole
vibrazione
in fase.
Alla
risonanza
w = w0
Vibrazione
di grande
ampiezza,
sfasata di
90°.
Sopra la
risonanza
w >> w0
Vibrazione
debole,
sfasata di.
180°.
L’Oscillatore Forzato:
Lo sfasamento tra la
nube elettronica e il
campo elettrico
dipende dalla
frequenza.
.
Siano w0 e w le frequenze
della nube elettronica e del
campo elettrico. La carica
dell’elettrone e’ negativa,
quindi c’e’ sempre uno
sfasamento di 180°
rispetto all’esempio
precedente.
Campo
elettrico
Nube
elettronica
Sotto la
risonanza
w << w0
Debole
vibrazione,
cn
sfasamento
di 180°.
Alla
risonanza
w = w0
Vibrazion
e molto
ampia,
con
sfasamen
to di -90°.
Al di sopra
della risonanza
w >> w0
Vibrazione
debole in
fase.
Lo sfasamento tra
la luce emessa e
luce incidente
dipende dalla
frequenza.
La luce emessa e’
sfasata di 90° rispetto al
moto dell’atomo.
Campo
elettrico
Sotto la
risonanza
w << w0
Nube
Campo
elettronic emesso
a
Emissione
debole,
sfasata di
90°.
Alla
risonanza
w = w0
Ampiezza di
emissione
grande,
sfasata di
180°.
Sopra la
risonanza
w >> w0
Emission
e debole,
sfasata di
-90°.
Oscillatore forzato: Matematica
Consideriamo un elettrone legato a una molla e in interazione con un campo
elettrico E0 exp(-iw t):
me d 2 xe / dt 2 mew02 xe eE0 exp(iwt )
La soluzione e’:
e / m
xe (t ) 2 e 2 E0 exp(iw t )
w0 w
E (t )
xe (t )
Quindi l’elettrone oscilla alla frequenza della radiazione incidente (w), ma
con ampiezza dipendente dalla differenza tra il quadrato della frequenza
propria dell’oscillatore e quella del campo elettrico.
Questo modello non e’ realistico
e / m
xe (t ) 2 e 2 E0 exp(iw t )
w0 w
Alla risonanza, quando
w = w0, xe tende
all’infinito.
E (t )
Questo non e’ realistico.
E’ necessario modificare
il modello.
xe (t )
Perche’ introduciamo il fattore di damping, g
Gli atomi decadono spontaneamente verso lo stato fondamentale.
Le vibrazioni di un materiale sono la somma delle vibrazioni di tutti gli atomi del
mezzo e le collisioni provocano degli sfasamenti, che sono all’origine
dell’attenuazione della vibrazione.
Atom #1
La sovrapposizione delle onde
sfasate determina un
decadimento esponenziale
dell’ampiezza delle vibrazioni e
quindi della luce emessa.
Atom #2
Atom #3
Sum:
time
La risposta di un atomo e’ approssimativamente
una Lorentziana complessa.
xe (t )
Infatti:
Assumendo
w
,w0
e / me
e / me
w02 w 2 iwg (w0 w )(w0 w ) iwg
si ha:
e / me
2w (w0 w ) iwg
e / me
1
2w (w0 w ) ig / 2
Definiamo w0 w e = g /2, e quindi
1/( – i ), e’ detta Lorentziana Complessa. Le sue parti reale e complessa
valgono:
1
1 i
i
2
2
2
i i i 2
Lorentziana Complessa
Ottica lineare: la dispersione della luce
La radiazione incidente modifica (polarizza) la nuvola elettronica: polarizzabilità è la tendenza a formare
un dipolo elettrico sotto l’azione di un campo elettrico
D
D
E
E
p qD e x
E=0
p
e2
E m w02 w 2 ) 2 2w 2
tan
w
w w
2
2
0
è la polarizzabilità
Possiamo legare micro a macro tramite la legge di Clausius-Mossotti (N densità atomica) e quindi
stabilire una relazione tra polarizzazione elettronica ed indice di rifrazione. Quindi n dipende dalla
frequenza della radiazione e.m. e dalle caratteristiche del materiale.
n 1 N
n 2 3
2
2
0
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Absorption
coefficient
Refractive
index
0
n–1
0
Frequency, w
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Dispersione normale nel visibile : lontano dall’assorbimento (ww0)
Coefficient
Value
B1
1.03961212
B2
2.31792344x10−1
B3
1.01046945
C1
6.00069867x10−3 μm2
C2
2.00179144x10−2 μm2
C3
1.03560653x102 μm2
Teoria di Sellmeier
Teoria di Cauchy
A,Bi,Ci= parametri empirici
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Materiali per l’ottica
Il vetro: effetti composizionali su trasmittanza
Esempio: la silice
L’incorporazione di Na2O porta alla presenza di
O non-pontanti (“difetti”)
L’energia di eccitazione degli elettroni varia
Allargamento e presenza di bande addizionali
intorno a 170nm
Ridotta trasmittanza nell’ultravioletto (filtro UV)
Materiali per l’ottica
Il vetro: effetti composizionali su n()
Se N vetri noti (indice di rifrazione ni e densità i) partecipano in percentuale di
peso ci alla formazione di un vetro, l’indice di rifrazione può essere calcolato con la
formula di Huggins e Sun (sovrapposizione lineare)
n ( ) 1 c n ( )
N
i 1
Il vetro avrà densità
c
N
i 1
i
i
Materiali per l’ottica
i
i
Il vetro: effetti composizionali su riflettanza
Riflettanza nell’ultravioletto
Dipende dalla composizione del
materiale.
Esempio: variazione della
riflettività di vetri silicati con il
contenuto di PbO
Materiali per l’ottica
Il vetro: effetti impurità su trasmittanza
Lo spettro di assorbimento dell’elemento dipende dalla sua valenza (donore/accettore)
Materiali per l’ottica
Il vetro: la diffusione
Materiali per l’ottica
Il vetro: la diffusione
Cause
1. Presenza di particelle non disciolte
2. Presenza di bolle o fasi diverse (devitrificazione)
3. Fluttuazioni di densità
La composizione e la tecnica di melting (dimensione delle impurezze
o disomogeneita’) influisce sull’esponente Iscat -m
m=3.4-4.8
Vetro crown (SiO2-CaO-Na2O)
Vetro flint (SiO2-PbO)
Materiali per l’ottica
m basso
m alto
Lenti oftalmiche
Potere diottrico
D
1
1
1
( n 1)
f
R1 R 2
R1
n= indice di rifrazione della lente
D>0
D<0
R2
raggi paralleli convergono dopo la lente
raggi paralleli divergono dopo la lente
Tipo di vetro utilizzato in passato: vetro crown con indice di rifrazione 1.523
Per forti disturbi visivi si utilizzano lenti a più alto indice di rifrazione per
diminuire il peso della lente e potenziare l’effetto visivo
(solo per poteri maggiori di 5/6D)
Materiali per l’ottica
Da: manuale per Ottica e Contattologia, A. Rossetti P. Gheller
Materiali ad alto indice di rifrazione normalmente sono più pesanti
Caratteristiche fisiche di un materiale di impiego nel campo oftalmico
Peso specifico
(densità)
Materiale
materiali vetrosi 2.4-4.5 g/cm3
materiali organici 1.1-1.4 g/cm3
Densità Indice di
Costringenza
rifrazione
@546nm
@546nm
Vetro crown
2.54
1.523
60
Vetro flint
3.60
1.620
36
Vetro flint pesante
4.004.20
1.650-2.000
29/32
Vetro flint di bario
3.303.80
1.600-1.680
44/46
Vetro fotocromatico alto
indice
2.70
1.600
42
Vetro fotocromatico
2.402.50
1.525
56/60
PMMA
1.191.21
1.490
57.5
1.32
1.498
56.0
1.20
1,590
29.5
CR-39
Materiali
per l’ottica
Policarbonato
Viscosità
importante nel processo di fabbricazione
Temperatura di fusione
industriali)
Materiali per l’ottica
importante nei materiali plastici (applicazioni
Materiale
Tfusione
(°C)
alluminio
660
argento
960
oro
1063
titanio
1668
platino
1773
Vetro crown
13001600
Acetato di cellulosa
(Xelox T)
160180
Acetoproprionato di
cellulosa (Ceroid)
150200
Altre caratteristiche di un materiale di impiego nel campo oftalmico
Chimiche
assorbimento di acqua
resistenza agli acidi
resistenza ai solventi
Termiche
resistenza al calore
coefficiente di dilatazione lineare
Meccaniche
materiale
durezza (resistenza all’impatto con un altro
misurata in scala di Mohs)
resistenza agli urti
Materiali per l’ottica
Proprietà delle lenti oftalmiche
1.
2.
3.
4.
Assenza di imperfezioni quali bolle, striature
Tolleranza nell’indice di rifrazione dei almeno 0.001 sul valore nominale
Tolleranza sul numero di Abbe tipicamente di 0.5 del valore nominale
Il coefficiente di dilatazione tra 20-300°C deve esser noto alla 3° cifra
Lenti in vetro:
•
•
Tipici vetri sono i soda-lime cui si aggiunge allumina o magnesia per
aumentare la durabilità chimica;
Per aumentare l’indice di rifrazione si aggiunge titania.
Lenti in organico:
•
I tipici materiali organici sono plastiche con elevata resistenza al graffio
Materiali per l’ottica