Document

Prova di esame di Fisica 4 - A.A. 2004/5 I prova in itinere 5/4/05
COGNOME…………..………………………
NOME. ……………........……….........
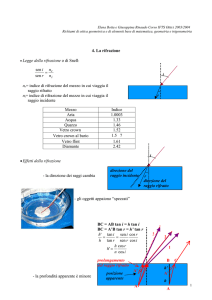
1) Un satellite geostazionario del sistema GPS irraggia nello spazio una potenza P = 500 W sotto forma di
onde radio monocromatiche non polarizzate. Assumendo che siano generate onde sferiche e che la
propagazione sia nel vuoto, si calcoli l’ampiezza del campo elettrico e del campo magnetico: (a) in
prossimità della superficie del mare sulla verticale del satellite, ovvero a distanza d = 36000 km dal satellite;
(b) nel punto della superficie del mare in cui la riflessione dalla superficie stessa risulta polarizzata
lineramente. Si assuma per l’acqua n = 2 alla frequenza del campo elettromagnetico.
d
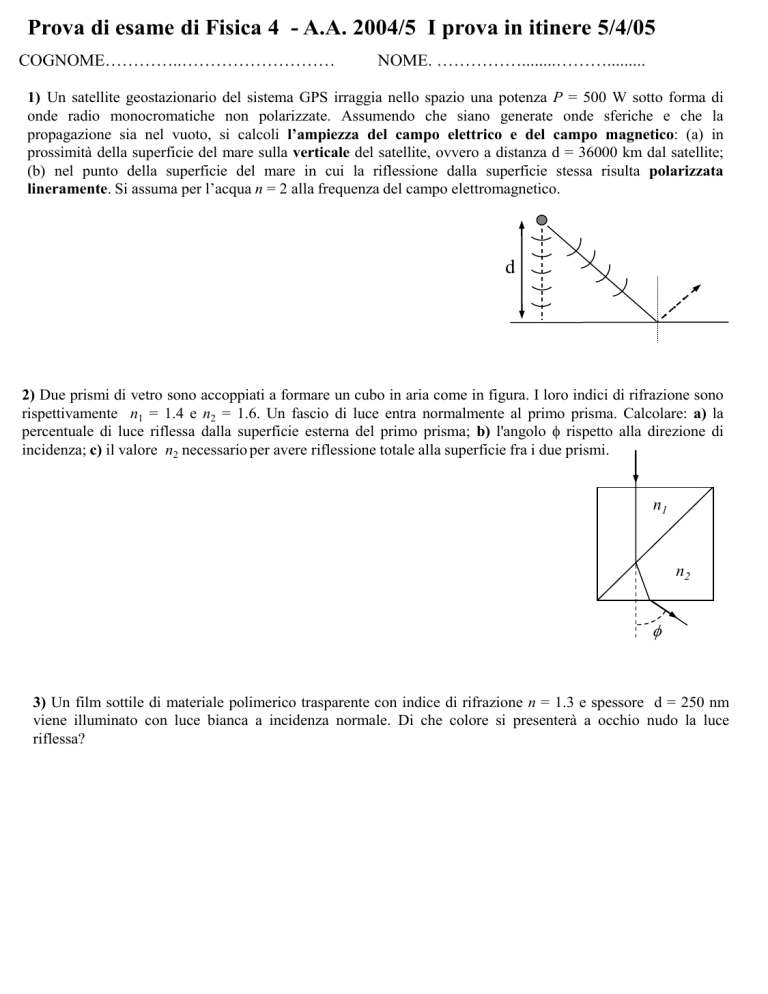
2) Due prismi di vetro sono accoppiati a formare un cubo in aria come in figura. I loro indici di rifrazione sono
rispettivamente n1 = 1.4 e n2 = 1.6. Un fascio di luce entra normalmente al primo prisma. Calcolare: a) la
percentuale di luce riflessa dalla superficie esterna del primo prisma; b) l'angolo  rispetto alla direzione di
incidenza; c) il valore n2 necessario per avere riflessione totale alla superficie fra i due prismi.
n1
n2

3) Un film sottile di materiale polimerico trasparente con indice di rifrazione n = 1.3 e spessore d = 250 nm
viene illuminato con luce bianca a incidenza normale. Di che colore si presenterà a occhio nudo la luce
riflessa?
QUESITI
(risposte max 30 parole ciascuna)
A) Si scriva l’equazione delle onde e la sua soluzione più generale per il campo elettrico.
B) Si scriva l’espressione del campo elettrico di un’onda monocromatica di frequenza ω e polarizzata
ellitticamente che si propaga lungo la direzione x in un mezzo con indice di rifrazione n.
C) Perché dei pezzi di vetro non colorato sono meno visibili quando immersi in acqua?
D) Scrivere la definizione e spiegare il significato fisico del vettore di Poynting.
E) Si disegni lo schema ottico di un interferometro di Michelson elencandone almeno un esempio di
applicazione.
Soluzioni
P  I 4 πr 2
1) In generale:
I
sulla verticale:
EV 

I
P
4πr 2
P
14
2

3
.
07

10
W/m
4πd 2
2 IV Z0  4.8 10-6 V m
BV 
E EV

 1.6 10-14 T
v
c
il secondo punto è definito dall’angolo di Brewster:
B  arctg
n
 63.4
1
d
d
rB 
cos  B
B
P
Pcos B 
I

 6.14 10 15 W/m 2
2
2
4πrB
4πd
2
EB 
2 I B Z0  2.15 10-6 V m
BB 
EB
 7.17 10-15 T
c
2) alla prima interfaccia vetro/aria si avrà:
2
 n  n   .4 
R   1 2   
  2.8 %
n

n
2
.
4

 1 2 
2
alla seconda interfaccia (vetro/vetro) si avrà rifrazione secondo Snell:
 n sin θi 
  38.2
θr  arcsin  1
n
2


n1
n2
d’altra parte, da semplici considerazioni trigonometriche ricaviamo per
l’ultimo angolo di incidenza:
θi '  45  θr  6.8

 n sin θi ' 
θr  arcsin  2
  10.9
1


Infine, dalla condizione di angolo limite:
n2

n1 sin θi  n  sin 45
1
ovvero:
n2

0.989
3)
dalla legge dell'interferenza a incidenza quasi normale su lamine sottili:
λ 0 ( I max ) 
4nd
(2m  1)
l’unico valore a cadere nel visibile è:
λ 0 ( I max ) 
4nd
 433 nm
3
corrispondente a una colorazione blu.
m  0, 1, 2, 3, .....