frequenza siano

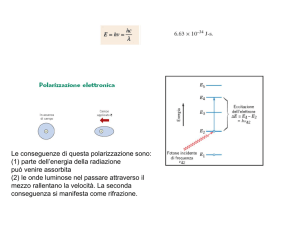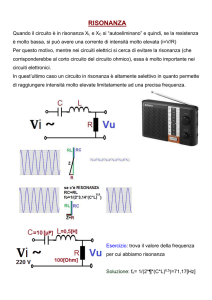
Le conseguenze di questa polarizzazione sono:
(1) parte dell’energia della radiazione
può venire assorbita
(2) le onde luminose nel passare attraverso il
mezzo rallentano la velocità. La seconda
conseguenza si manifesta come rifrazione.
Perche’ introduciamo il fattore di damping, g
Gli atomi decadono spontaneamente verso lo stato fondamentale.
Le vibrazioni di un materiale sono la somma delle vibrazioni di tutti gli atomi del
mezzo e le collisioni provocano degli sfasamenti, che sono all’origine
dell’attenuazione della vibrazione.
Atom #1
La sovrapposizione delle onde
sfasate determina un
decadimento esponenziale
dell’ampiezza delle vibrazioni e
quindi della luce emessa.
Atom #2
Atom #3
Sum:
time
Forza
L’Oscillatore Forzato:
Lo sfasamento tra
l’oscillatore e la forza
dipende dalla frequenza.
Siano w0 la frequenza
dell’oscillatore, e w quella della
forza.
Oscillatore
Sotto la
risonanza
w << w0
Debole
vibrazione
in fase.
Alla
risonanza
w = w0
Vibrazione
di grande
ampiezza,
sfasata di
90°.
Sopra la
risonanza
w >> w0
Vibrazione
debole,
sfasata di.
180°.
L’Oscillatore Forzato:
Lo sfasamento tra la
nube elettronica e il
campo elettrico
dipende dalla
frequenza.
.
Siano w0 e w le frequenze
della nube elettronica e del
campo elettrico. La carica
dell’elettrone e’ negativa,
quindi c’e’ sempre uno
sfasamento di 180°
rispetto all’esempio
precedente.
Campo
elettrico
Nube
elettronica
Sotto la
risonanza
w << w0
Debole
vibrazione,
cn
sfasamento
di 180°.
Alla
risonanza
w = w0
Vibrazion
e molto
ampia,
con
sfasamen
to di -90°.
Al di sopra
della risonanza
w >> w0
Vibrazione
debole in
fase.
Lo sfasamento tra
la luce emessa e
luce incidente
dipende dalla
frequenza.
La luce emessa e’
sfasata di 90° rispetto al
moto dell’atomo.
Campo
elettrico
Sotto la
risonanza
w << w0
Nube
Campo
elettronic emesso
a
Emissione
debole,
sfasata di
90°.
Alla
risonanza
w = w0
Ampiezza di
emissione
grande,
sfasata di
180°.
Sopra la
risonanza
w >> w0
Emission
e debole,
sfasata di
-90°.
La risposta di un atomo e’ approssimativamente
una Lorentziana complessa.
e / me
e / me

w02  w 2  iwg (w0  w )(w0  w )  iwg
Infatti:
xe (t ) 
Assumendo
 ,w 0 si ha:
w
e / me

2w (w0  w )  iwg

e / me
1
2w (w0  w )  ig / 2
Definiamo   w0  w e  = g /2, e quindi
1/( – i ), e’ detta Lorentziana Complessa. Le sue parti reale e complessa
valgono:
1
1   i

i

 2
 2
2
  i   i   i       2
Ottica lineare: la dispersione della luce
La radiazione incidente modifica (polarizza) la nuvola elettronica: polarizzabilità è la tendenza a formare
un dipolo elettrico sotto l’azione di un campo elettrico
D
D
E
E
p  qD  e x
E=0
p
e2
 

E m w02  w 2 ) 2   2w 2

tan  

w
w w
2
2
0
 è la polarizzabilità
Possiamo legare micro a macro tramite la legge di Clausius-Mossotti (N densità atomica) e quindi
stabilire una relazione tra polarizzazione elettronica ed indice di rifrazione. Quindi n dipende dalla
frequenza della radiazione e.m. e dalle caratteristiche del materiale.
n  1 N

n  2 3
2
2
0
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Dispersione normale nel visibile : lontano dall’assorbimento (ww0)
Coefficient
Value
B1
1.03961212
B2
2.31792344x10−1
B3
1.01046945
C1
6.00069867x10−3 μm2
C2
2.00179144x10−2 μm2
C3
1.03560653x102 μm2
Teoria di Sellmeier
Teoria di Cauchy
A,Bi,Ci= parametri empirici
Materiali per l’ottica
Ottica lineare: la dispersione della luce
Materiali per l’ottica
Il vetro: effetti composizionali su n()
Se N vetri noti (indice di rifrazione ni e densità i) partecipano in percentuale di
peso ci alla formazione di un vetro, l’indice di rifrazione può essere calcolato con la
formula di Huggins e Sun (sovrapposizione lineare)
n(  )  1    c n (  )
N
i 1
Il vetro avrà densità
  c 
N
i 1
i
i
Materiali per l’ottica
i
i