ESERCIZI DI STATISTICA DESCRITTIVA
(In collaborazione con la dott.ssa Giulia Sbianchi)
I seguenti 10 esercizi possono essere risolti facendo i calcoli con la calcolatrice in tempi ragionevoli. Ai fini
della propria preparazione generale, gli Studenti potrebbero in aggiunta implementarli in Excel. Il grado di
difficoltà dei 20 esercizi è omogeneo.
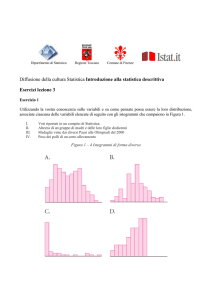
Esercizio 1.
Data la seguente serie di dati su Lunghezza e Genere di 8 lucertole muraiole, per ciascuno dei due caratteri
costruire la tabella di frequenza (per la variabile lunghezza prendere 140-|160, 160-|170, 170-|200 come
classi). Rappresentare, inoltre, le due distribuzioni con un opportuno grafico.
id
1
2
3
4
5
6
7
8
Lunghezza, mm
165
157
168
178
171
182
182
153
Sesso: 1=M, 2=F
M
F
F
M
F
M
M
F
Esercizio 2.
Calcolare la lunghezza media delle 8 lucertole dell’esercizio 1. Utilizzare prima la serie di dati individuale e,
successivamente, ripetere i calcoli partendo dalla tabella di frequenza. Ci aspettiamo che i due
procedimenti diano dei valori per la media differenti? Perché?
Esercizio 3.
Calcolare la lunghezza mediana delle 8 lucertole dell’esercizio 1. Utilizzare prima la serie di dati individuale
e, successivamente, ripetere i calcoli partendo dalla tabella di frequenza.
Esercizio 4.
Calcolare la deviazione standard della lunghezza delle 8 lucertole dell’esercizio 1. Utilizzare prima la serie di
dati individuale e, successivamente, ripetere i calcoli partendo dalla tabella di frequenza.
Esercizio 5.
Calcolare il campo di variazione (range) e l’intervallo interquartilico della lunghezza delle 8 lucertole
dell’esercizio 1. (Utilizzare la serie dei dati individuali)
Esercizio 6.
Una dieta sperimentale per elefanti in età adulta viene utilizzata in due diversi centri A e B; gli elefanti del
centro A sono 25 e hanno un’età media pari a 54 anni mentre quelli trattati nel centro B sono 62 e hanno
un’età media di 58 anni. Qual è l’età media generale degli elefanti che hanno ricevuto la nuova dieta?
Corso introduttivo di Statistica. Simona Iacobelli
1
Esercizio 7.
In riferimento ai due centri A e B dell’esercizio precedente, sappiamo anche che la varianza dell’età era la
stessa per entrambi i centri e pari a 64. Possiamo dire che la variabilità dell’età degli elefanti sia la stessa
per entrambi i centri?
Esercizio 8.
Calcolare la media e la mediana della distribuzione del numero di Capsule di Petri in 31 laboratori differenti
riportata nella tabella seguente:
Capsule
1–|10
10–|20
20–|40
40–|60
n
6
8
13
4
31
Esercizio 9.
Rappresentare con un grafico opportuno la distribuzione del numero di Capsule di Petri dell’esercizio
precedente.
Esercizio 10.
8 donne entro il 4° mese in gravidanza sono state seguite da un dietologo, che ha riportato per ciascuna il
seguente peso (in Kg): 64.3; 65.2; 70.0; 54.5; 58.8; 81.5; 61.0; 62.0. Calcolare la media e la mediana. I dati
suggeriscono una forte asimmetria della distribuzione del peso?
Esercizio 11.
La produzione di grossi trasformatori e condensatori elettrici richiede l’impiego di sostanze tossiche (PCB),
molto pericolose quando vengono disperse nell’ambiente. Nelle vicinanze di un lago vi è un impianto di
grosse dimensioni che, per motivi di sicurezza, viene chiuso per due settimane. Si vogliono confrontare i
livelli di PCB in 6 pesci del lago (trattenuti in una gabbia a fini scientifici) prima e dopo la chiusura
dell’impianto. I risultati delle misurazioni sono riportati sotto.
Prima
13.0
12.8
11.0
13.2
12.5
11.9
Dopo
9.4
11.5
11.5
13.1
10.2
12.0
Esercizio 12.
In riferimento ai 6 pesci dell’esercizio precedente di cui si conoscono i livelli di PCB prima e dopo la chiusura
dell’impianto, calcolare la deviazione standard sia per le variabili “prima” e “dopo” sia per la riduzione
media: vale la linearità?
Corso introduttivo di Statistica. Simona Iacobelli
2
Esercizio 13.
Uno scienziato ha registrato la temperatura in un campione di 132 unità statistiche, la media espressa in
gradi Celsius (C ) era pari a 14.2 con una deviazione standard di 7.8. Adesso un suo collega statunitense gli
chiede di riportargli i risultati in gradi Fahrenheit (F): può lo scienziato rispondere velocemente, sapendo
che F = C*1.8 + 32?
Esercizio 14.
Si riportano l’età, il FEV1 (Forced Espiratory volume in 1 second) e la pressione diastolica per 10 maschi
adulti. Calcolare la mediana e la deviazione standard per queste tre variabili. Utilizzare un opportuno indice
per confrontare la variabilità di questi tre caratteri.
Età
25
32
28
21
33
33
34
24
41
26
FEV1
2.5
1.8
1.5
2.5
4.5
2.1
3.4
1.2
2.8
3.9
Pressione
85
71
92
80
87
83
70
101
90
83
Esercizio 15.
È stato condotto un test cognitivo all’interno di un labirinto su un campione di cavie per valutare in quanto
tempo riuscissero a percorrere un certo tracciato. I quartili del tempo misurato in minuti erano 13, 28 e
47, rispettivamente. Questo significa che:
o 1 su 4 ha impiegato meno di … minuti;
o 1 su 4 ha impiegato più di … minuti;
o 2 su 4 ha impiegato tra i … e i … minuti;
o La metà ha impiegato più di … minuti.
Esercizio 16.
Questo esercizio richiede la conoscenza delle proprietà della distribuzione Normale (solitamente trattate nel
parte di corso riguardante la Teoria della probabilità)
Con riferimento ai dati dell’esercizio precedente, oltre ai quartili del tempo sappiamo anche che la media e
la deviazione standard erano rispettivamente pari a 30 e 8 minuti. Possiamo dire se la distribuzione del
tempo sia approssimativamente Normale? Qual è l’indice di posizione più appropriato per dare una
descrizione sintetica della distribuzione?
Corso introduttivo di Statistica. Simona Iacobelli
3
Esercizio 17.
Il grafico illustra la distribuzione dell’Età di 173 pazienti all’insorgenza della malattia. Costruire la
corrispondente tabella di frequenza e calcolare la media.
Esercizio 18.
Calcolare l’età mediana per i pazienti dell’esercizio precedente: possiamo dire che la distribuzione è
asimmetrica? Individuare, inoltre, le classi contenenti il primo e il terzo quartile.
Esercizio 19.
Vengono raccolti campioni da 105 corsi d’acqua per valutarne la concentrazioni di stronzio (mg/ml). I corsi
d’acqua vengono classificati a seconda del livello di stronzio: 28 a bassa concentrazione (dai 18 ai i 29
mg/ml), 42 a media concentrazione (dai 30 ai 65 mg/ml) e, infine, 35 ad alta concentrazione (dai 66 ai 99
mg/ml). La concentrazione media in ciascun gruppo è di 21.83, 48.30 e 76.77, con deviazione standard pari
a 0.98, 2.12 e 3.08, rispettivamente. Qual è il gruppo più omogeneo rispetto alla concentrazione di
stronzio? Qual è la concentrazione media generale?
Corso introduttivo di Statistica. Simona Iacobelli
4
Esercizio 20.
Il seguente grafico è stato utilizzato in un libro per mostrare la distribuzione la distribuzione della lunghezza
dei sepali in due diverse specie di Iris.
Nel libro, oltre al grafico, è stata allegata questa tabella per dare ulteriori informazioni sulla variabile:
$Setosa
Min.
4.300
Q1.
4.500
Mediana
5.000
Media
5.199
Q3.
5.200
Max.
5.800
$Virginica
Min.
Q1.
4.500
6.225
Mediana
6.500
Media
6.588
Q3.
6.382
Max.
7.900
4 dei dati riportati in tabella sono sbagliati. Sapresti individuarli?
Corso introduttivo di Statistica. Simona Iacobelli
5
Soluzioni
Esercizio 1.
Carattere: Sesso
Modalità
M
F
Totale
Frequenza
4
4
8
Percentuali
50%
50%
100%
Essendo Sesso un carattere qualitativo sconnesso, non bisogna calcolare le frequenze percentuali
cumulate.
La distribuzione può essere rappresentata, ad esempio, attraverso un grafico a barre (in basso a sinistra),
costituito da una colonna per ciascuna delle due modalità M e F, di altezza pari alla frequenza percentuale
corrispondente. È buona norma lasciare che l’asse verticale delle percentuali vada da 0 a 100 per evitare
distorsioni nella percezione delle frequenze.
N.B. I rettangoli devono essere separati.
Carattere: Lunghezza (mm)
Modalità
140 -| 160
160 -| 170
170 -| 200
Tot
Freq
assoluta
2
2
4
8
Freq
percentuale
25%
25%
50%
100%
Freq
cumulata
2
4
8
Freq cumulata
percentuale
25%
50%
100%
Ampiezza
classe
20
10
30
Densità di
frequenza
= 2/20=0.1
= 2/10=0.2
= 4/30=0.13
Le ultime due colonne sono state aggiunte alla tabella di frequenza per poter costruire l’istogramma (in
basso a destra). Infatti, la distribuzione può essere rappresentata attraverso un istogramma delle
frequenze, costituito da tre rettangoli contigui, ciascuno disegnato in corrispondenza degli estremi della
relativa classe, di altezza pari alla densità di frequenza. In questo modo l’area del rettangolo corrisponde
alla frequenza della classe.
Esercizio 2.
La media per la lunghezza è data da (165+157+…+153) / 8 = 1356 / 8 = 169.5
Corso introduttivo di Statistica. Simona Iacobelli
6
Per ottenere la media a partire dalla tabella di frequenza, è necessario prima calcolare il valore centrale
della classe:
Lunghezza
140 -| 160
160 -| 170
170 -| 200
Totale
Freq assoluta nj
2
2
4
8
Freq relativa fj
0.25
0.25
0.50
1.00
Valore centrale xj
xj · nj
150
165
185
300
330
740
1370
xj · fj *
37.5
41.25
92.5
171.25
*N B: è possibile saltare un passaggio se si moltiplica il valore centrale della classe per la frequenza relativa
e non per la cumulata. In questo caso la media è data dalla somma dei singoli prodotti xj · fj.
Media = 1370 / 8 = 171.25
Quando non abbiamo la serie di dati individuali ma solo le frequenze associate alle classi, il calcolo della
media è approssimato perché implicitamente assumiamo che tutti i valori contenuti nella classe siano
uguali al valore centrale (Vedi anche ES 8).
Esercizio 3.
Per poter calcolare la mediana occorre ordinare le osservazioni in ordine crescente: 153 157 165 168 171
178 182 182.
n/2 = 4 essendo 4 un numero pari, prendiamo le osservazioni che occupano la quarta e la quinta
posizione e calcoliamo la mediana facendo la media tra i due valori: (168 + 171)/2 = 339/2 = 169.5.
Partendo dalla tabella di frequenza , osserviamo che la mediana si trova nella classe 160 -| 170, ossia la
classe entro la quale si trova il 50% della distribuzione (oppure la classe in cui la frequenza cumulata
raggiunge il 50%). Il calcolo approssimato della mediana è dato da: 160 + (4-2)/2 ·(170-160) = 170.
Esercizio 4.
La seguente tabella contiene i calcoli necessari per ottenere la deviazione standard nel caso dei dati
individuali
id
Lunghezza,
mm
x^2
1
165
27225
2
157
24649
3
168
28224
4
178
31684
5
171
29241
6
182
33124
7
182
8
Tot
Tot/n
153
1356
169.5
Numeratore della varianza = 230680 – 8· (169.5^2) = 838
Varianza = 838 /7 = 119.7143
Deviazione standard = sqrt(119.7143) = 10.9414
33124 Utilizziamo ora la tabella di frequenza:
23409
230680
28835
Corso introduttivo di Statistica. Simona Iacobelli
7
Lunghezza
140 -| 160
160 -| 170
170 -| 200
Tot
Tot / n
Freq. assoluta nj
2
2
4
8
Freq. relativa fj
0.25
0.25
0.50
1.00
Valore central xj
150
165
185
xj^2 · nj
45000
54450
136900
236350
29543.75
Ripetiamo I calcoli visti in precedenza per la serie dei dati individuali. In questo caso la media è pari a
171.25, che è il valore della media ottenuto partendo dalla tabella di frequenza:
Numeratore della varianza = 236350 – 8· (171.25^2) = 1737.5
Varianza = 1737.5 /7 = 248.2143
Deviazione standard = sqrt(248.2143) = 15.75482
Esercizio 5.
Il campo di variazione è ottenuto come differenza tra il valore massimo e il valore minimo della
distribuzione. Dunque, nel nostro caso è pari a 182 – 153 = 29.
Per poter calcolare l’intervallo interquartilico è necessario prima individuare Q1 e Q3, che sono dati dalle
modalità che occupano la posizione 8/4 = 2 e 8*3/4 = 6, rispettivamente. Quindi Q1 = 157 e Q3 = 178.
IQR = 178 – 157 = 21.
Esercizio 6.
L’età media generale degli elefanti che hanno ricevuto la dieta sperimentale è ottenuta come media
ponderata delle due medie (54 e 58) con pesi pari alle numerosità dei due gruppi (25 e 62).
Media generale = (54*25 + 58*62) / (25+62) = 4946 / 87 = 56.85
Esercizio 7.
La risposta corretta è no perché il valore della media è diversa tra i due centri. Per valutare meglio la
variabilità dell’età tra i due centri possiamo utilizzare il coefficiente di variazione:
Deviazione standard: sqrt(64) = 8 in entrambi i gruppi;
CV nel gruppo A = 8/54 = 14.8%;
CV nel gruppo B = 8/58 = 13.8%.
C’è, dunque, una piccola differenza e la distribuzione dell’età degli elefanti del centro B risulta essere più
omogenea.
Esercizio 8.
La variabile “Numero di Capsule di Petri” è una variabile quantitativa discreta, che in questo caso viene
trattata come se fosse una continua poiché assume molte modalità (varia da 1 a 60); infatti la distribuzione
è rappresentata attraverso una tabella di frequenza per un carattere in classi.
Per calcolare la media è necessario prima individuare il valore centrale per ogni classe, ottenuto come
(estremo inf + estremo sup)/2. Successivamente si calcola l’ammontare complessivo di capsule in ciascuna
classe come prodotto tra il valore centrale e la rispettiva frequenza. La media è data dal rapporto tra
l’ammontare complessivo di capsulein tutte le classi e la numerosità del campione, che è pari a 31.
Corso introduttivo di Statistica. Simona Iacobelli
8
Per individuare la mediana, o meglio la classe che contiene la mediana, utilizziamo le frequenze cumulate.
Valore Ammontare
centrale
xi · ni
5.5
33.0
Freq
cumulata
6
Capsule
n
1 –| 10
6
10 –| 20
8
15
120
14
20 –| 40 13
30
390
27
40 –| 60
50
200
31
4
31
743
Media = 743/31 = 23.97
Mediana: modalità che occupa il posto 32/2 = 16.
- facendo riferimento alla colonna delle frequenze cumulate, possiamo notare che la mediana appartiene
alla classe 20-|40; infatti la prima classe include solo 6 unità e se aggiungiamo le unità della seconda
arriviamo a un totale di 14 unità.
- Possiamo anche stimare la mediana anche assumendo che la frequenza necessaria a raggiungere la
mediana sia uniformemente distribuita all’interno dell’intervallo che corrisponde alla classe mediana:
(mediana – estr. inf.) : (ampiezza intervallo classe mediana) = (freq tra estremo infer e mediana N/2 – C) :
(freq classe mediana)
(X – 20) : (40 – 20) = (31/2 – 14) : (13) mediana = 20 + [(40 – 20)* (15.5 – 14)]/13 = 22.3
Esercizio 9.
La distribuzione può essere rappresentata attraverso un istogramma con rettangoli contigui di base pari
all’ampiezza della classe e altezza data dalla rispettiva densità. I calcoli vengono illustrati nella seguente
tabella:
Ampiezza
Capsule
n
densità
classe
0.67
1 –| 10
6
9
10 –| 20
8
10
0.80
20 –| 40
13
20
0.65
40 –| 60
4
20
0.20
31
Corso introduttivo di Statistica. Simona Iacobelli
9
Esercizio 10.
Per calcolare la mediana ordiniamo le osservazioni e individuiamo le modalità di posto 4 e 5 (9/2 = 4.5).
Un altro metodo per illustrare questa procedura di calcolo consiste nel disporre le osservazione in una
tabella e attribuire a ciascuna modalità il rispettivo rango:
Valore x1
64.3
65.2
70
54.5
58.8
81.5
61
62
rango ri
5
6 Somma dei valori = 517.3 Media = 517.3 / 8 = 64.66
7
1 Valore centrale (rango 4 e 5): 62 e 64.3 Mediana = (62 + 64.3) / 2 = 63.15
2
8
3
4
Per valutare l’asimmetria della distribuzione possiamo confrontare la media e la mediana: in una
distribuzione simmetrica queste due misure sono molto vicine. In questo caso la distanza tra la media e la
mediana è pari a 1.51. Per valutare se e quanto questa distanza sia grande, dobbiamo confrontarla con la
deviazione standard, che è una sorta di “unità di misura relativa” della variabile .
Calcoliamo la deviazione standard:
Valori al
Valore xi
quadrato xi
64.3
4134.49
Somma dei quadrati (SS) = 33,920.47
65.2
4251.04
Numeratore della varianza = 33,920.47 – 8 ·64.662 = 470.5588
70
4900.00
Varianza = 470.5588 / 7 = 67.2227
54.5
2970.25
Dev. St. = 8.1989
58.8
3457.44
81.5
61
62
6642.25
3721.00
3844.00
Corso introduttivo di Statistica. Simona Iacobelli
10
Confrontandola con la deviazione standard, possiamo affermare che la differenza media – mediana è
piccola, dunque i dati non suggeriscono un’asimmetria della distribuzione.
Esercizio 11.
La Riduzione media corrisponde alla differenza tra il valore “Prima” e il valore “Dopo”; quando osserviamo
un aumento della variabile X (PCB) tra prima e dopo, la riduzione è negativa.
Possiamo calcolare la riduzione per ogni pesce e poi ne facciamo una media aritmetica:
Prima
Somma
Somma/6
Dopo
Riduzione
13.0
9.4
3.6
12.8
11.5
1.3
11.0
11.5
-0.5
13.2
13.1
0.1
12.5
10.2
2.3
11.9
74.4
12.4
12.0
67.7
11.28333
12.4-11.3=
-0.1
6.7
1.116667
1.116667
Un’altra possibile soluzione consiste nel calcolare la riduzione sfruttando la proprietà della linearità: date le
variabili X1 e X2, se applichiamo una trasformazione lineare del tipo Y = aX1 + bX2 è sempre verificato che
media(Y) = a·media(X1)+b·media(X2).
In questo esercizio, Y è la riduzione ed è una trasformazione lineare di X1= Prima e X2= Dopo con a pari a 1
e b pari a -1. La media della differenze tra media è, dunque, uguale a
media(Prima - Dopo)= media(Prima)-media(Dopo).
Un altro modo di illustrare la proprietà della linearità della media aritmetica consiste nell’affermare che
mediaa bx a bx . Questo implica, ad esempio, che se consideriamo una trasformazione lineare
della variabile X, spostando il valore sull’asse e cambiando l’unità di misura, possiamo calcolare la media
della variabile trasformata Y=a+bX semplicemente trasformando la media della variabile originale.
Esercizio 12.
Il calcolo della deviazione standard per le variabili “Prima” e “Dopo” è lasciato agli studenti. I risultati sono
0.822912 and 1.313646, rispettivamente.
Per la Riduzione Media utilizziamo la formula “rapida”:
Corso introduttivo di Statistica. Simona Iacobelli
11
Prima
Dopo
Riduzione Riduzione^2
13
9.4
3.6
12.96
12.8
11.5
1.3
1.69
11
11.5
-0.5
0.25
13.2
13.1
0.1
0.01
12.5
10.2
2.3
5.29
11.9
12
-0.1
0.01
Sum
74.4
67.7
6.7
20.21
Sum/6
12.4
11.2833
1.11667
3.36833
La varianza è: 20.21 - 6·media^2
var 20.21 6 1.11667 2
1
2.5456
6 1
E la deviazione standard è la sua radice quadrata: 1.595
Quindi, per la deviazione standard la proprietà della linearità non è verificata in quanto il suo calcolo
richiede operazioni di elevamento al quadrato e estrazione della radice che non godono della proprietà
matematica di linearità:
a bx 2 a 2 bx 2
Esercizio 13.
Senza dover trasformare tutti i valori della temperatura da C a F e poi calcolare media e deviazione
standard, lo scienziato può rapidamente ricorrere alle proprietà delle trasformazioni lineari (una già
ricordata nell’esercizio 11).
Si può calcolare la temperatura media in gradi Fahreneit applicando la trasformazione lineare alla media in
C: media in F = media in C ·1.8+32 = 57.56.
Questa proprietà non è valida nel calcolo della deviazione standard, ma sappiamo di una proprietà delle
varianze: varianza in F = varianza in C ·1.82 = 7.82 ·1.82 =197.1216 dev.st. in F=14.04
Esercizio 14.
Le tre variabili sono tutti caratteri quantitativi. La media aritmetica è ottenuta come somma dei valori divisi
per la numerosità del collettivo, 10. Per la deviazione standard possiamo utilizzare la formula “rapida”. I
calcoli vengono illustrati nella tabella seguente.
Per confrontare la variabilità dei tre caratteri NON è sufficiente far riferimento alle sole deviazioni standard
perché le variabili misurano fenomeni diversi e sono espresse in unità di misura diverse. È, perciò,
necessario esprimere le deviazioni standard in termini relativi rispetto alla media, utilizzando il coefficiente
di variazione.
Corso introduttivo di Statistica. Simona Iacobelli
12
Id
Età
1
2
3
4
5
6
7
8
9
10
Somma
Somma/10
25
32
28
21
33
33
34
24
41
26
297
29.7
FEV1
Pressione
2.5
85
1.8
71
1.5
92
2.5
80
4.5
87
2.1
83
3.4
70
1.2
101
2.8
90
3.9
83
26.2
842
2.62
84.2
Varianza
Dev. St.
cv
Età^2
FEV1^2 Pressione^2
625
6.25
7225
1024
3.24
5041
784
2.25
8464
441
6.25
6400
1089
20.25
7569
1089
4.41
6889
1156
11.56
4900
576
1.44
10201
1681
7.84
8100
676
15.21
6889
9141
78.70
71678
914.1
7.87
7167.8
35.57
1.12
86.84
5.96
1.06
9.32
20%
40%
11%
Il carattere con la variabilità più elevata è FEV1, 4 volte più variabile della Pressione e 2 volte dell’Età
(notare che FEV1 ha la deviazione standard più bassa).
Esercizio 15.
o
o
o
o
1 su 4 ha impiegato meno di 13 minuti: questa è la definizione di primo quartile, ¼=25% di valori
osservati inferiori a Q1=13;
1 su 4 ha impiegato più di 47 minuti: analogamente, questa è la definizione di terzo quartile,
¾=75% di valori osservati superiori a Q3 = 47;
2 su 4 hanno impiegato tra i … e i … minuti possibili risposte: “tra 0 e la mediana di 28 minuti”; “
tra Q1 e Q3” e “tra la mediana di 28 minuti e il tempo massimo” ( anche se non conosciamo il
valore massimo dei minuti impiegati);
La metà ha impiegato meno di 28: questa è la definizione di Mediana.
Esercizio 16.
Per prima cosa possiamo notare che la media (30) e la mediana (20) sono molto vicine, difatti la loro
distanza pari a 2 è piccola se confrontata con la deviazione standard (=2/8). Dunque, la distribuzione è
simmetrica.
Ma la Normale non è l’unica distribuzione simmetrica, perciò dobbiamo appurare che risultino verificate
anche le altre proprietà. In una distribuzione Normale il primo e il terzo quartile devono essere posti a una
distanza dalla media pari a 0.67 volte la deviazione standard, ossia nel nostro caso 0.67*8 = 5. Quindi, se la
distribuzione fosse approssimativamente Normale il primo e il terzo quartile dovrebbero essere 25 e 35. I
quartili osservati, tuttavia, sono 13 e 47, decisamente più distanti dalla media rispetto a quelli che
avremmo osservato se la distribuzione fosse stata una Normale con la stessa media e la stessa varianza.
In conclusione la nostra distribuzione non è approssimativamente Normale, è simmetrica ma non ha una
forma a campana. Potrebbe trattarsi di una distribuzione con code alte e pochi valori al centro,
probabilmente una distribuzione bimodale.
Dato quanto detto, né la media né la mediana sono indici di posizione adeguati per descrivere la
distribuzione; se questa fosse bimodale, dovremmo utilizzare le due mode e se riconoscessimo la presenza
di due sottopopolazioni, dovremmo utilizzare le media e la mediana per le due popolazioni.
Corso introduttivo di Statistica. Simona Iacobelli
13
Esercizio 17.
Il grafico riportato è un istogramma, dunque ogni classe è rappresentata sull’asse orizzontale e la rispettiva
frequenza è pari all’area del rettangolo corrispondente. L’altezza del rettangolo è uguale alla densità di
frequenza in ogni classe.
Iniziamo mettendo le informazioni in una tabella:
Ampiezza
Densità di
Età
della
frequenza
classe
20 |- 30
10
2.10
30 |- 40
10
3.70
40 |- 70
30
1.60
70 |- 90
20
3.35
Per ogni classe otteniamo la frequenza assoluta come prodotto tra la densità di frequenza e l’ampiezza
della classe.
Per la media calcoliamo il prodotto tra la frequenza assoluta e il valore centrale della classe:
Ampiezza
Densità di
Valore
Età
della
Frequenza
x * freq
frequenza
centrale x
classe
20 |- 30
10
2.10
21
25
525
30 |- 40
10
3.70
37
35
1295
40 |- 70
30
1.60
48
55
2640
70 |- 90
20
3.35
67
80
5360
173
9820
Media = 9820/173 = 56.76
Esercizio 18.
Per individuare la classe contenente il primo, il secondo e il terzo quartile calcoliamo prima le frequenze
percentuali cumulate:
Età
frequenza %
N
cum%
20-30
21
12.1%
21
12.1%
30-40
37
21.4%
58
33.5%
40-70
48
27.7%
106
61.3%
70-90
67
38.7%
173 100.0%
173
La mediana è tra i 40 e i 70 anni, Q1 tra i 30 e i 40 e Q3 tra 70 e 90.
Un valore esatto per la mediana è dato da: 40 + (173/2 – 58)/48 ·(70-40) = 57.81
Corso introduttivo di Statistica. Simona Iacobelli
14
Non è facile dire se la distribuzione sia simmetrica o meno solo guardando l’istogramma perché ci sono
troppe poche classi. Possiamo, però, verificare se e quanto la mediana sia vicina alla media (56.76); per
questo abbiamo bisogno di calcolare la deviazione standard:
Valore
Età
freq
centrale
x2
x2 * freq
x
13,125
20 |- 30
21
25
625
30 |- 40
37
35
1225
45,325
40 |- 70
48
55
3025 145,200
70 |- 90
67
80
6400 428,800
173
632,450
Numeratore della Varianza = 632,450 – 173· (56.76^2) = 75,037.28
Varianza =75,037.28 /172 = 436.2633
Deviazione standard = sqrt(436.2633) = 20.88692
La deviazione standard è alquanto elevata, quindi la differenza tra media e mediana è piccola. Questo ci
permette di concludere a favore della simmetria. Da notare, comunque, che la distribuzione sembra essere
bimodale, perciò né la media né la mediana sono degli indicatori adeguati a descriverla.
Esercizio 19.
L’indice di variabilità utilizzato per valutare l’omogeneità della distribuzione è il coefficiente di variazione
(cv = deviazione standard espressa in termini percentuali sulla media). La media generale è calcolata come
media ponderata delle medie di ogni classe con pesi pari alla numerosità dei gruppi. I calcoli vengono
riportati nella tabella che segue.
Il gruppo più omogeneo è quello dei corsi d’acqua a media concentrazione di stronzio, sebbene la loro
variabilità sia di poco inferiore di quelli ad alta concentrazione. Il gruppo a bassa concentrazione è quello
più variabile.
La media generale è 5326.79 / 105 = 50. 73
Concentrazione di
stronzio
n
media
Dev. St. n*media cv
Bassa (18-29)
28
21.83
0.98
611.24
16.0%
Media (30-65)
42
48.3
2.12 2028.60
10.5%
Alta (66-99)
35
76.77
3.08 2686.95
11.5%
Totale
105
5326.79
Esercizio 20.
I numeri sbagliati sono
- Nel gruppo “Setosa” (boxplot blu, sotto):
o Il primo quartile Q1: 4.500 è troppo piccolo. Guardando il boxplot possiamo notare che Q1
è intorno a 4.800.
o La media: non può essere 5.199, ci aspettiamo che coincida con la mediana perché il
boxplot suggerisce che questa sia una distribuzione decisamente simmetrica;
- Nel gruppo del trapianto allogenico (boxplot verde, sopra):
o Il Minimo: non può essere 4.500, è troppo piccolo. Il grafico mostra la presenza di un
Corso introduttivo di Statistica. Simona Iacobelli
15
o
outlier, evidenziato con un pallino al di fuori del baffo ma il suo valore è intorno a 4.900;
Il terzo quartile Q3: 6.382 < 6.500 che è la mediana. Per definizione la mediana è inferiore
al tero quartile.
Infatti, la tabella corretta è:
$Setosa
Min.
4.300
Q1.
4.800
$Virginica
Min.
Q1.
4.900
6.225
Mediana
5.000
Media
5.006
Mediana Media
6.500
6.588
Q3.
5.200
Max.
5.800
Q3.
6.900
Max.
7.900
Corso introduttivo di Statistica. Simona Iacobelli
16