CORSO DI FISICA ASPERIMENTALE II ESERCIZI SU FORZA DI LORENTZ E LEGGE DI BIOT SAVART Docente: Claudio Melis 1) 2) 3) 4) Due correnti rispettivamente di intensità pari a 5 A e 4 A percorrono due fili conduttori che sono posti perpendicolarmente tra di loro. Considerando un punto P, interno ai due fili, che dista 15 cm dal filo percorso da 4 A e 10 cm da quello percorsi dai 5 A, calcolare il campo magnetico risultante in quel punto. Svolgimento I due fili di cui parla il problema sono posti perpendicolarmente nel piano e le correnti che attraversano entrambi i conduttori sono dello stesso verso, in quanto positive. Ora è possibile determinare il valore del campo magnetico generato da un filo percorso da corrente tramite la legge di Biot Savart:
mentre sappiamo che la direzione delle linee di campo sono circonferenze concentriche attorno al filo. Invece il verso delle linee di campo è legato al verso della corrente tramite la regola della mano destra: se il pollice segue il verso della corrente, allora le dita indicano il verso di quelle che sono le linee del campo magnetico:
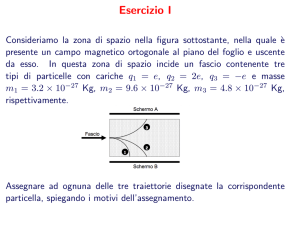
Ora, poichè ognuno dei due fili presenti nel problema sono percorsi da corrente, entrambi genereranno campi che saranno uno entrante nel foglio ed uno uscente, se stabiliamo che le correnti abbiano verso diretto verso l'alto: I dati a nostra disposizione sono: i1 = 5 A i2 = 4 A d1 = 10 cm = 10 · 10-­‐2 m = 10-­‐1 m d2 = 15 cm = 15 · 10-­‐2 m Calcoliamo tramite la legge di Biot Savart l'intensità dei due campi magnetici: Nell'ipotesi di correnti disposte come in figura, prendiamo come positivo il verso entrante nel foglio, quello di B1, e come negativo il verso di B2, per cui il campo risultante totale è la somma vettoriale dei due campi: L'equazione scalare corrispondente alla precedente equazione vettoriale è: Bris = B1 – B2 = ( 1 – 0,53) · 10-­‐5 T = 0,47 · 10-­‐5 T Per cui il campo magnetico risultante ha intensità pari a 0,47 · 10-­‐5 T e verso entrante nel foglio 5) L'intensità del campo magnetico prodotto da una spira circolare di raggio R nel suo centro è pari al campo magnetico misurato a 40 cm di distanza da un filo rettilineo percorso da corrente. Determinare il raggio R della spira sapendo che essa ed il filo sono percorsi dalla stessa corrente i. Lo svolgimento del problema richiede la conoscenza del calcolo del modulo del campo magnetico per una spira circolare e per un filo percorso da corrente. Il campo magnetico creato da una spira circolare percorsa da una corrente è pari a: in cui R è il raggio della spira. Mentre in prossimità di un filo percorso da corrente il campo B vale: anche conosciuta come legge di Biot–Savart. I dati forniti sono i seguenti: d = 40 cm ispira = ifilo Bspira = Bfilo Per cui uguagliando i due campi otteniamo: in definitiva il raggio della spira percorsa dalla stessa corrente del filo, creante un campo magnetico di intensità pari a quella misurata a 40 cm dal filo, ha un raggio di 126 cm. 6) Un protone inizialmente fermo viene accelerato attraverso una ddp di 2500 V e viene immesso in una regione dello spazio in cui è presente un campo magnetico di intensità 0,3 T. Determinare il raggio della traiettoria circolare che il protone percorre nel campo Svolgimento I dati a nostra disposizione sono: ΔV = 2500 V mp = 1,67 ·10-­‐27 Kg (massa del protone) q = 1,6 ·10-­‐19 C (carica del protone) B = 0,3 T in seguito alla differenza di potenziale il protone acquisisce un'energia pari a: E = q · ΔV = 1,6 ·10-­‐19 · 2500 = 4 ·10-­‐16 J Tale energia ha solo componente cinetica, per cui la velocità con cui il protone penetra nel campo è pari a: E = K = ½ · m · v2 da cui All'interno del campo magnetico, la forza di Lorentz che agisce sulla carica in movimento eguaglierà la forza centripeta che permette il moto circolare per cui: Florentz = Fcentripeta da cui q · V · B · senα = m · V2 / R in cui q è la carica della particella V la sua velocità B l'intensità del campo magnetico α l'angolo tra v e B e dato che l'angolo è 90, sen90=1 m la massa della particella R il raggio della traiettoria circolare. Ricaviamo dunque il raggio della traiettoria: R = (m · V)/( q · B · sen α) = (1,67 ·10-­‐27 · 6,9 · 105 ) / (1,6 ·10-­‐19 · 0,3) = 24 · 10-­‐3 m Dunque il raggio della traiettoria descritta dal protone all'interno del campo magnetico è pari a 24 · 10-­‐3 m. 6) Un elettrone viene accelerato attraverso un campo elettrico facendogli raggiungere una velocità di 1,6 ·106 m/s. L'elettrone dunque percorre una zona di spazio in cui è presente un campo magnetico uniforme le cui linee di forza sono perpendicolari alla velocità della particella. Calcolare il modulo del campo magnetico necessario affinché l'orbita circolare percorsa dall'elettrone abbia un raggio di 9,1 cm. Svolgimento La situazione fisica descritta dal problema è quella relativa ad un elettrone dotato di velocità v che si muove in un campo magnetico le cui linee di forza sono perpendicolari alla velocità: I dati a nostra disposizione sono: m = 9,1 ·10-­‐31 Kg (massa dell'elettrone) e = 1,6 ·10-­‐19 C (carica dell'elettrone) v = 1,6 ·106 m/s R = 9,1 cm = 9,1 ·10-­‐2 m Sulla carica in moto nel campo magnetico agirà la forza di Lorentz, la cui direzione sarà perpendicolare alla velocità con cui l'elettrone penetra nel campo. Dunque la traiettoria seguita dall'elettrone sarà di tipo circolare e la composizione dei due moti (moto circolare uniforme e moto rettilineo uniforme), darà luogo ad una traiettoria elicoidale: Ora la forza di Lorentz eguaglierà la forza centripeta che permette il moto circolare per cui: Florentz = Fcentripeta Da cui q · V · B · senα = m · V2 / R in cui q è la carica della particella V la sua velocità B l'intensità del campo magnetico α l'angolo tra v e B, essendo perpendicolari α = 90 e quindi sen90 = 1 m la massa della particella R il raggio della traiettoria circolare. Riordinando i termini e semplificando otteniamo che: B = (m · V) / ( q · R) = (9,1 ·10-­‐31 · 1,6 ·106) / (1,6 ·10-­‐19 · 9,1 ·10-­‐2) = 10-­‐4 T Per cui l'intensità del campo magnetico che permette di mantenere l'elettrone su un'orbita circolare di raggio 9,1 cm è pari a 10-­‐4 T. 7) Uno spettrometro di massa è un particolare dispositivo per misurare la massa di particelle cariche. La particella dotata di carica, viene accelerata fornendole un'energia cinetica ben precisa e quindi una velocità. La carica penetra così in un campo B, noto, ortogonalmente e a causa della forza di Lorentz viene deviata e costretta a descrivere una traiettoria semicircolare, riemergendo in un punto ove è presente una lastra fotografica. Misurando la distanza tra l'ingresso e l'uscita della particella se ne può determinare la massa. In che modo? Svolgimento Lo spettrometro di massa di cui parla il problema ha il seguente schema: La carica viene accelerata e portata alla velocità V. Una volta fatta entrare in una regione in cui è presente il campo B uscente dal foglio e con linee di forza perpendicolari alla velocità V, la carica risentirà della forza di Lorentz per cui devierà la sua traiettoria rettilinea in una curvilinea. Ora poichè la particella penetra perpendicolarmente nel campo, possiamo affermare che la distanza tra il punto di ingresso e quello di uscita è esattamente pari al diametro della circonferenza che la carica percorrerebbe per intero se rimanesse confinata all'interno del campo. La forza di Lorentz eguaglierà la forza centripeta che permette il moto circolare per cui: Florentz = Fcentripeta da cui q · V · B · senα = m · V2 / R in cui q è la carica della particella V la sua velocità B l'intensità del campo magnetico α l'angolo tra v e B, essendo perpendicolari α = 90 e quindi sen90 = 1 m la massa della particella R il raggio della traiettoria circolare. Riordinando i termini e semplificando otteniamo che la massa è pari a: m = (q · B · R)/V q, B, R e V sono tutte variabili note. Combinandole in questo modo riusciamo pertanto a determinare la massa della particella carica. Due correnti di intensità pari a 4 A e 10 A percorrono due fili rettilinei paralleli che distano 4 cm tra di loro. Calcolare la forza per unità di lunghezza che ogni filo esercita sull'altro. Considerare il caso di correnti concordi e discordi per determinarne infine il verso. Svolgimento La situazione fisica descritta dal problema è quella di due fili infinitamente lunghi e paralleli percorsi da corrente. In tale contesto sappiamo che due fili rettilinei paralleli percorsi da corrente si attraggono con una forza di modulo pari a
i1 e i2 sono le correnti che percorrono i fili L la lunghezza dei fili d la loro distanza. Il problema chiede di calcolare la forza per unità di lunghezza per cui la formula precedente si modifica così: Scriviamo i dati del problema: i1 = 4 A i2 = 10 A d = 4 cm = 4 · 10-­‐2 m Dunque avremo: Per determinare infine il verso della forza, ovvero se questa è attrattiva o repulsiva tra i due fili, si ricorre alla regola della mano destra. Le forze di interazione tra i due fili sono attrattive se le due correnti sono concordi, repulsive se discordi:
2) All'interno di un avvolgimento formante un solenoide lungo 50 cm è misurato un campo magnetico pari a 252·10-­‐6 T. Se il solenoide è percorso da una corrente di 10 A calcolare il numero di avvolgimenti del solenoide. Svolgimento Il campo creato da un solenoide percorso da corrente elettrica è pari a
n cui N è il numero di avvolgimenti presenti nel solenoide ed L la sua lunghezza. Ora i dati che il problema ci fornisce sono i seguenti: i = 10 A L = 50 cm = 0,5 m B = 252·10-­‐6 T Ricaviamo dalla formula inversa di B l'espressione che ci consente di calcolare N: