Esercizi sulle reti elettriche in corrente continua

Esercizi sulle reti elettriche in corrente continua
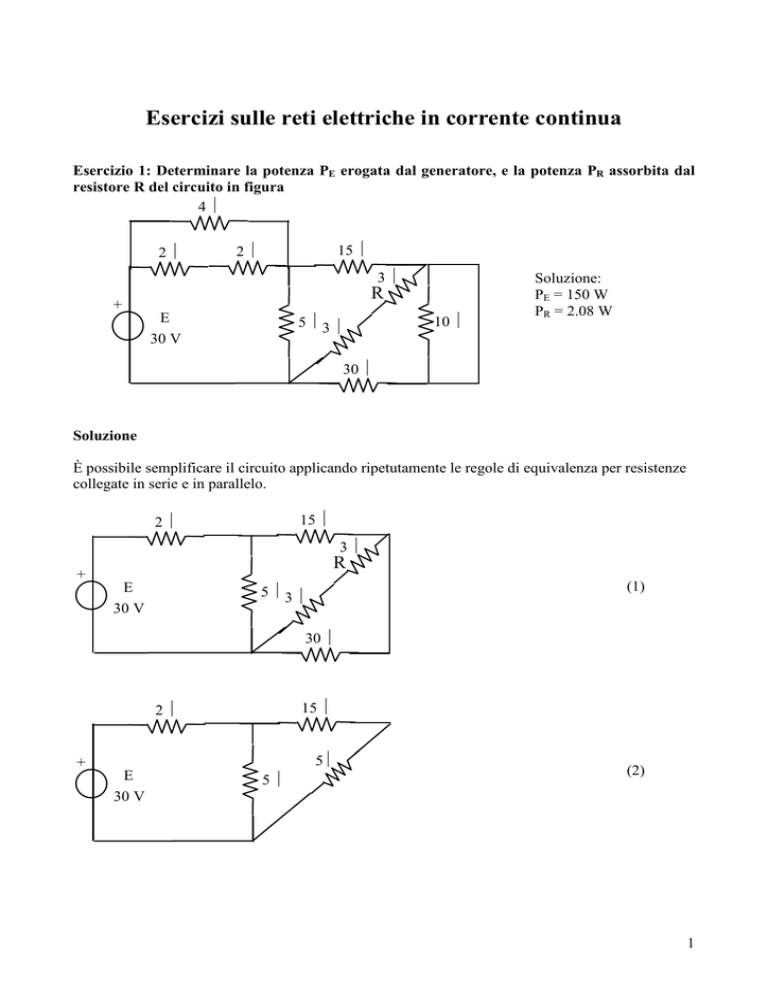
Esercizio 1: Determinare la potenza PE erogata dal generatore, e la potenza PR assorbita dal
resistore R del circuito in figura
4Ω
2Ω
15 Ω
2Ω
3Ω
+
R
E
30 V
5 Ω3 Ω
10 Ω
Soluzione:
PE = 150 W
PR = 2.08 W
30 Ω
Soluzione
È possibile semplificare il circuito applicando ripetutamente le regole di equivalenza per resistenze
collegate in serie e in parallelo.
15 Ω
2Ω
3Ω
+
R
E
30 V
(1)
5 Ω3 Ω
30 Ω
15 Ω
2Ω
+
5Ω
E
30 V
5Ω
(2)
1
2Ω
+
E
30 V
5Ω
(3)
20 Ω
Ia
+
+
E
30 V
6Ω
(4)
Dal circuito elementare (4) si ricava:
I a = 30 / 6 = 5 A
La potenza assorbita dal generatore vale:
PE assorb = E ⋅ (− I a ) = −150 W
ovvero, la potenza erogata dal generatore vale:
PE erog = − PE assorb = 150 W
Procedendo a ritroso, è possibile determinare la corrente iR che attraversa il resistore R. Considerato
il circuito (3), si ha:
2Ω
Ia
+
+
E
30 V
Ic
Ib
(5)
+
5Ω
20 Ω
I a = Ib + Ic

5 I b = 20 I c
⇒ Ib = 4 A, Ic = 1 A
Considerato il circuito (1), si può scrivere:
2
Vc
2Ω
+ 15 Ω
+
+
E
30 V
3 Ω+
Ic
Ia
Vb
R
Ib
5 Ω3 Ω +
(6)
Id
Vd
30 Ω
Vb − Vc − Vd = 0
dove:
Vb = 5 ⋅ I b = 20 V
Vc = 15 ⋅ I c = 15 V
Vd = (3 + 3) ⋅ I d
per cui si ricava:
Id =
20 − 15
= 0.833 A
6
La potenza assorbita dal resistore risulta:
PR = R I d =
2
25
= 2.08 W
12
Esercizio 2: Risolvere la rete in figura e verificare il bilancio delle potenze
i1
v1
i3
A
v2
v3
i2
2Ω
2A
6Ω
+
Soluzione:
I1 = 2 A
I2 = -4.5 A
I3 = 2.5 A
24 V
B
Soluzione
Il circuito è costituito da R=3 rami e N=2 nodi.
3
I rami 2 e 3 sono controllati sia in tensione che in corrente (è possibile esprimere la tensione del ramo in funzione della corrente del ramo stesso e viceversa). Il ramo 1, essendo presente il generatore
di corrente, è controllato in tensione ma non in corrente.
Metodo di Tableau
Incognite
− R tensioni di ramo
− R correnti di ramo
− N-1 potenziali di nodo
Totale: 2R+N-1
Equazioni
− R equazioni indipendenti applicando la LKT ai rami
− N-1 equazioni indipendenti applicando la LKC ai nodi
− R equazioni costitutive dei rami
Totale: 2R+N-1
Si sceglie il nodo B come nodo di riferimento (eB = 0).
 v1 = e A

v 2 = e A
v = e
A
 3
R equazioni indipendenti applicando la legge di Kirchhoff delle tensioni ai rami
{i1 +i2 + i3 = 0
N-1 equazioni indipendenti applicando la legge di Kirchhoff
delle correnti ai nodi
i1 = 2

 v 2 = 24 + 2i 2
 v = 6i
3
 3
R equazioni costitutive dei rami
Si ottengono 7 equazioni indipendenti nelle 7 incognite (v1, v2, v3, i1, i2, i3, eA).
Metodo delle equazioni di Kirchhoff (maglie fondamentali)
Incognite
− R tensioni di ramo
− R correnti di ramo
Totale: 2R
Equazioni
− R-N+1 equazioni indipendenti applicando la legge di Kirchhoff delle tensioni alle maglie fondamentali
− N-1 equazioni indipendenti applicando la
legge di Kirchhoff delle correnti ai nodi
− R equazioni costitutive dei rami
Totale: 2R
Si traccia un albero del grafo, e si determinano le R-N+1 maglie fondamentali (in questo caso 2):
A
− Rami di albero: N-1=1
− Rami di coalbero: R-N+1=2
− Numero di maglie fondamentali: R-N+1=2
B
4
 − v1 + v 2 = 0

− v 2 + v 3 = 0
R-N+1 equazioni indipendenti applicando la legge di Kirchhoff delle tensioni alle maglie fondamentali:
{i1 + i2 + i3 = 0
N-1 equazioni indipendenti applicando la legge di Kirchhoff
delle correnti ai nodi
i1 = 2

 v 2 = 24 + 2i2
 v = 6i
3
 3
R equazioni costitutive dei rami
Sostituendo le equazioni costitutive nelle equazioni di
Kirchhoff si ottiene quindi un sistema di R equazioni indipendenti rispettivamente in R incognite di corrente oppure di tensione di ramo.
− v1 + 24 + 2i2 = 0

− 24 − 2i2 + 6i3 = 0
2 + i + i = 0

2
3
Si ottengono 3 equazioni indipendenti nelle 3 incognite (v1, i2, i3).
Metodo dei tagli fondamentali
Incognite
− R-N+1 correnti dei rami di coalbero
− Rncc tensioni incognite dei rami non controllati in corrente (in cui non è possibile
esprimere la tensione in funzione della
corrente utilizzando la caratteristica)
Totale: R-N+1+ Rncc
Equazioni
− R-N+1 equazioni indipendenti applicando la legge di Kirchhoff delle tensioni alle maglie fondamentali. Sui rami controllati in corrente, le tensioni sono espresse
in funzione delle correnti dei rami di coalbero (mediante le equazioni costitutive
dei rami e le equazioni di Kirchhoff delle
correnti ai tagli fondamentali).
− Rncc equazioni caratteristiche dei rami
non controllati in corrente
Totale: R-N+1+ Rncc
Nel caso del circuito in esame Rncc = 1.
Si traccia un albero del grafo, e si determinano le R-N+1 maglie fondamentali (in questo caso 2):
A
− Rami di albero: N-1=1
− Rami di coalbero: R-N+1=2
− Numero di maglie fondamentali: R-N+1=2
B
Espressione delle correnti dei rami d’albero in funzione delle correnti dei rami di coalbero mediante
le N-1 equazioni di Kirchhoff delle correnti applicate ai tagli fondamentali (in questo caso 1):
5
{i1 +i 2 + i 3 = 0
I1
I1
I3
A
ATT: in questo caso particolare l’equazione al
taglio fondamentale coincide con l’equazione di
Kirchhoff delle correnti applicata al nodo A. In
generale invece l’applicazione della legge di
Kirchhoff delle correnti ai tagli fondamentali determina un sistema di equazioni nelle correnti in
forma diversa da quella che si ottiene applicando
la legge di Kirchhoff delle correnti ai nodi. I due
sistemi di equazioni sono comunque equivalenti,
essendo sempre possibile ottenere la forma delle
equazioni di uno mediante combinazioni lineari
delle equazioni dell’altro.
I2
B
− v1 + 24 + 2(− i1 − i3 ) = 0

− 24 − 2(− i1 − i3 ) + 6i3 = 0
{ i1 = 2
⇒ i 2 = − i1 − i 3
R-N+1 equazioni indipendenti applicando la legge di Kirchhoff delle tensioni alle maglie fondamentali
caratteristica del ramo non controllato in corrente
Si ottengono 3 equazioni indipendenti nelle 3 incognite (v1, i1, i3).
Metodo dei potenziali di nodo
Incognite
− N-1 potenziali di nodo
− Rnct correnti incognite dei rami non controllati in tensione (in cui non è possibile
esprimere la corrente in funzione dei potenziali di nodo utilizzando le equazioni
caratteristiche dei rami del circuito)
Totale: N-1+ Rnct
Equazioni
− N-1 equazioni indipendenti applicando la
legge di Kirchhoff delle correnti ai nodi.
Sui rami controllati in tensione, le correnti sono espresse in funzione dei potenziali
di nodo (mediante le equazioni costitutive dei rami e le equazioni di Kirchhoff
delle tensioni ai rami)
− Rnct equazioni caratteristiche dei rami non
controllati in tensione
Totale: N-1+ Rnct
Nel caso del circuito in esame Rnct = 0.
Si sceglie il nodo B come nodo di riferimento (eB = 0).
Espressione delle tensioni di ramo in funzione dei potenziali di nodo
mediante le equazioni di Kirchhoff delle tensioni ai rami.
 v1 = e A

v 2 = e A
v = e
A
 3
Espressione delle correnti di ramo in funzione dei potenziali di nodo mediante le R equazioni costitutive e le R equazioni di Kirchhoff delle tensioni ai rami (per tutti i rami del circuito in esame è
possibile ricavare direttamente la corrente di ramo in funzione dei potenziali di nodo):
6

i = 2
 1
 v 2 = e A = 24 + 2i 2
 v = e = 6i
A
3
 3

2+

i1 = 2

e
⇒ i2 = A − 12
2

e
i3 = A

6
N-1 equazioni indipendenti applicando la legge di Kirchhoff delle correnti ai nodi
eA
e
− 12 + A = 0
2
6
Si ottiene 1 equazione in 1 incognita (eA).
Risolvendo si ha:
2
eA − 10 = 0 ⇒ e A = 15V
3
Per verificare il bilancio delle potenze come richiesto dall’esercizio calcoliamo le correnti di ramo e
le tensioni di ramo. La potenza assorbita da ogni ramo, visto che sono stati utilizzati i versi di riferimento associati con la scelta dell’utilizzatore, si ottiene dal prodotto delle relative tensione e corrente:
ramo
v
i
p
1
15 V
2A
30 W
2
15 V −4.5 A − 67.5 W
3
15 V 2.5A
37.5 W
Il bilancio delle potenze è quindi verificato (p1 + p2 + p3 = 0).
Per il ramo 2 si ha inoltre: pR = vR iR = R iR2 = 2 (4.5)2 = 40.5 W (assorbita), pE = E i2 = 24 (−4.5) =
− 108 W (assorbita, in quanto i2 è entrante nel terminale positivo del generatore di tensione). Anche
il bilancio di potenza sul ramo 2 è soddisfatto:
40
.53
W + ( −108W ) = −
67
W
12
4
2.54
3
1424
3 1
potenza
assorbita
dal
resistore
potenza
assorbita
dal
generatore
potenza
assorbita
dal
ramo
ovvero
108
W − 40
.53
W = 67
.53
W
123
12
12
potenza
erogata
dal
generatore
potenza
assorbita
dal
resistore
potenza
erogata
dal
ramo
7
Esercizio 3: Determinare la tensione tra i punti A e B del circuito in figura
Suggerimento: semplificare il circuito utilizzando le formule per collegamenti in serie e in parallelo.
3Ω
1Ω
A
4Ω
Soluzione:
VBA = 14.7 V
10 A
3Ω
B
2Ω
20 V
+
3Ω
Esercizio 4: Determinare la potenza dissipata dal resistore R5 del circuito in figura.
Suggerimento: utilizzare la trasformazione stella triangolo:
A
A
R3
100 Ω
+
R1
100 Ω
E
+
E
100 V
D
C
B
R4
60 Ω
R5
26 Ω
RD
11.5 Ω
RC
11.5 Ω
100 V
C
I4
R2
40 Ω
RA
44.25 Ω
B
I2
R4
60 Ω
D
R2
40 Ω
Soluzione:
V2
( R I − R2 I 2 ) 2
P5 = CD = 4 4
= 0.24W
R5
R5
8
Esercizio 5.a: Determinare il bipolo equivalente di Thevenin tra i punti B e C del circuito in
figura e calcolare la corrente che circola attraverso il resistore R5 .
Esercizio 5.b: Determinare il bipolo equivalente di Norton tra i punti B e C del circuito in figura e calcolare la corrente che circola attraverso il resistore R5.
Soluzione 5.a:
B
Req
6Ω
B
+
E1
R5
50 V
6Ω
I2
I1
I5 = 6 A
C
Soluzione 5.b:
B
2A
3A
R3
6Ω
Eeq
72 V
C
A
R5
R6
2Ω
4Ω
Req
6Ω
Ieq
D
R5
6Ω
I5 = 6 A
12 A
C
Esercizio 6.a: Determinare il dipolo equivalente di Norton tra i punti E e F del circuito in figura e calcolare la corrente che circola attraverso il resistore R9.
Esercizio 6.b: Determinare il dipolo equivalente di Thevenin tra i punti E e F del circuito in
figura e calcolare la corrente che circola attraverso il resistore R9.
Soluzione 6.a:
E
I9
− 1.67 A
R2=10 Ω
A
E
R5=2 Ω
Req
8Ω
Ieq
R6=4 Ω
B
R9
4Ω
2.5 A
I9
F
R9
I1
4Ω
6A
E
Soluzione 6.b:
30 V
+
E
Req
F
D
R8=10 Ω
I2=7 A
8Ω
R7=5 Ω
C
Eeq
20 V
R9
4Ω
I5 = − 1.67 A
F
9
Esercizio 7.a: Determinare il dipolo equivalente di Thevenin tra i punti C e D del circuito in
figura e calcolare la potenza dissipata dal resistore R5 del circuito in figura.
Esercizio 7.b: Determinare il dipolo equivalente di Norton tra i punti C e D del circuito in figura e calcolare la potenza dissipata dal resistore R5 del circuito in figura.
Soluzione 7.a:
C
Req
66.1 Ω
A
R3
100 Ω
+
D
C
B
R4
60 Ω
R5
26 Ω
26 Ω
Eeq
8.93 V
R1
100 Ω
E
100 V
R5
I5 = 97 mA
D
Soluzione 7.b:
C
R2
40 Ω
Ieq
R5
26 Ω
Req
66.1 Ω
I5 = 97 mA
135 mA
D
P5 = R5 I 5 2 = 0.24W
10