Grafico velocità – tempo

Grafico velocità – tempo (v-t) - Analisi
Si prende in considerazione un corpo che si muove lungo una retta con moto vario, quindi il
corpo cambia velocità nel tempo. Si definisce accelerazione una quantità che indica come la
velocità cambia nel tempo. Se v1 e v2 sono le velocità istantanee del corpo agli istanti t1 e t2, allora
l’accelerazione media, am, per definizione, vale:
am 
v v finale  v iniziale v 2  v 1


t t finale  t iniziale
t1  t 2
m  s   L  T 
2
2
Se al trascorrere del tempo vengono riportati su di un grafico i valori delle velocità, è possibile
ricavare sia l’accelerazione sia lo spazio percorso dal corpo.
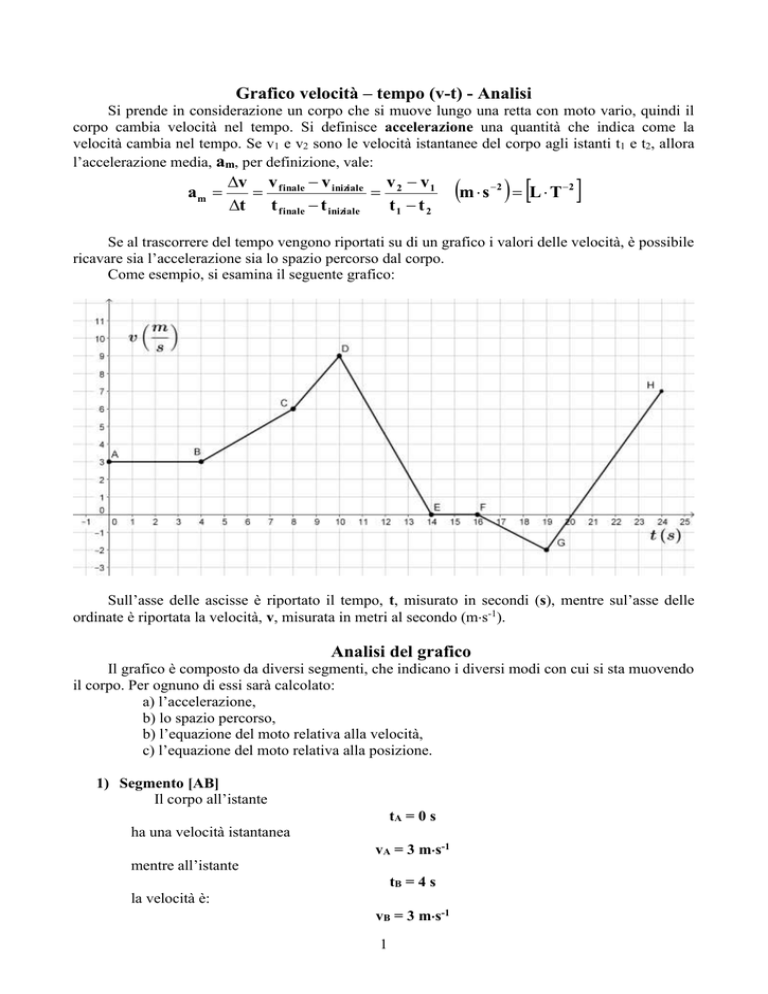
Come esempio, si esamina il seguente grafico:
Sull’asse delle ascisse è riportato il tempo, t, misurato in secondi (s), mentre sul’asse delle
ordinate è riportata la velocità, v, misurata in metri al secondo (ms-1).
Analisi del grafico
Il grafico è composto da diversi segmenti, che indicano i diversi modi con cui si sta muovendo
il corpo. Per ognuno di essi sarà calcolato:
a) l’accelerazione,
b) lo spazio percorso,
b) l’equazione del moto relativa alla velocità,
c) l’equazione del moto relativa alla posizione.
1) Segmento [AB]
Il corpo all’istante
tA = 0 s
ha una velocità istantanea
vA = 3 ms-1
mentre all’istante
tB = 4 s
la velocità è:
vB = 3 ms-1
1
Nell’intervallo di tempo
t AB  t B  t A
La velocità si mantiene costante
v A  v B  3 m  s 1
ed il moto risulta uniforme. Pertanto la accelerazione è nulla.
Dalle conclusioni effettuate, si deduce che un segmento parallelo all’asse delle
ascisse (asse del tempo) sta ad indicare che la velocità è costante nell’intervallo
considerato ed il corpo si muove di moto rettilineo uniforme.
Calcolo dello spazio percorso
Nel moto rettilineo uniforme lo spazio percorso, s, dal corpo in un certo intervallo
di tempo, t, vale:
s  v  t
La figura di fianco mostra il dettaglio del
grafico v-t relativo al segmento [AB].
Mettendo a confronto l’espressione per
calcolare lo spazio percorso ed il grafico, si nota che
il prodotto:
v  t
Non è altro che l’area del rettangolo le cui
dimensioni sono la velocità e l’intervallo di tempo.
Una delle dimensioni del rettangolo è il segmento,
[AB], che descrive il moto del corpo. Pertanto si può
generalizzare il risultato affermando che, nel grafico
velocità-tempo, lo spazio percorso dal corpo in un
certo intervallo di tempo si calcola misurando
l’area della porzione di piano che si trova sotto la curva che descrive il moto vario.
Quando si analizzeranno gli altri casi, il concetto sarà approfondito.
Sia adoperando l’espressione del moto rettilineo uniforme sia l’area sotto il
segmento [AB], il valore dello spazio percorso è sempre lo stesso. Essendo
t  4s
e
m
v3
s
Lo spazio percorso è:


s AB  v  t  3m  s 1  4s   12m
Calcolo dell’equazione relativa alla posizione
L’equazione del moto rettilineo uniforme è:
s  v  t  s0
dove:
v = velocità del corpo (costante);
s0 = posizione iniziale del corpo, ovvero la posizione che il corpo all’istante iniziale t=0s
(costante)
t = istante di tempo (variabile);
s = posizione occupata dal corpo ad un certo istante di tempo t.
2
Supponendo all’istante iniziale (tinizio= 0s) il corpo si trova coincidente con
l’osservatore, per cui
s0 = 0m
l’equazione del moto rettilineo uniforme è:
s AB  3  t
Sintesi dei risultati segmento [AB]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[AB], sono
a) l’accelerazione: l’accelerazione è nulla (aAB=0ms-2) poiché si è in presenza di un
Moto Rettilineo Uniforme (MRU).
b) lo spazio percorso: s=12m;
b) l’equazione del moto relativa alla velocità: la velocità è costante e la sua equazione è:
vAB = 3 ms-1 = costante
c) l’equazione del moto relativa alla posizione:
s AB  3  t
3
2) Segmento [BC]
Nell’intervallo di tempo:
t BC  t C  t B  (8s)  (4s)  4s
la velocità passa, in modo uniforme, da un valore iniziale
v B  3m  s 1
ad un valore finale
v C  6m  s 1
La variazione di velocità, vBC, è uniforme, cioè varia costantemente, poiché la
linea congiunge i due punti B e C è un segmento. Nell’intervallo di tempo tBC il corpo
accelera con un’accelerazione, aBC, pari a:
v BC v C  v B
6m  s 1  3m  s 1
3m  s 1
a BC 



 0,75m  s 2
8s  4s 
t BC
tC  tB
4s
Calcolo dello spazio percorso [BC]
Graficamente lo spazio percorso nell’intervallo di tempo tBC si calcola, come
detto in precedenza, misurando l’area della porzione di piano che si trova sotto il
segmento [BC].
L’area da calcolare è quella di un
trapezio, dove le basi sono le velocità
iniziale, vB, e finale, vC, e l’altezza è
l’intervallo di tempo tBC. Quindi:

 

s BC 
s BC 
v B  v C   t
2
 6m  s 1  4s 
 18m
2
3m  s  
1

Calcolo dell’equazione del moto relativa alla velocità [BC]
Dal momento che il moto del corpo è rappresentato da un segmento, l’equazione
del moto avrà la stessa forma dell’equazione di una retta:
v BC  a BC  t  v 0
dove:
vBC = velocità del corpo ad ogni istante dell’intervallo di tempo tBC;
aBC = accelerazione nell’intervallo di tempo tBC, il cui valore è: aBC=0,75ms-2;
t = generico istante di tempo;
v0 = velocità che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre di un
Moto Rettilineo Uniformemente Accelerato (MRUA). Il valore di tale velocità deve
essere calcolato.
Per calcolare v0, si parte dalla seguente considerazione: Della retta passante per i punti B
e C si conoscono le coordinate sia di B, [B(4s, 3ms-1)] sia di C [C(8s, 6ms-1)].
Pertanto, sostituendo le coordinate di uno dei due punti nell’equazione della velocità, si
trova il valore di v0. Sostituendo le coordinate di B si ottiene:
v BC  a BC  t  v 0
v B  a BC  t B  v 0
4
3  0,75  4  v 0 ,
3  3  v0
v 0  0m  s 1
Quindi l’equazione del moto relativa alla velocità è:
v BC  0,75  t
Calcolo dell’equazione del moto relativa alla posizione [BC]
L’equazione del moto rettilineo uniformemente accelerato relativa alla posizione,
nel caso generale, è:
s BC 
1
 a BC  t 2  v 0  t  s 0
2
dove.
sBC = posizione del corpo ad ogni istante dell’intervallo di tempo tBC;
aBC = accelerazione nell’intervallo di tempo tBC, il cui valore è: aBC=0,75ms-2;
t = generico istante di tempo;
v0 = velocità del corpo avrebbe all’istante t0 se si muovesse sempre di MRUA,
(v0= 0ms-1);
s0 = posizione che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre
di MRUA. Il valore di tale posizione deve essere calcolato.
Il metodo del calcolo della posizione s0 è simile a quello effettuato per il calcolo della
velocità v0. Si prende in considerazione il punto B, si nota che i parametri da introdurre
nell’equazione sono:
tB = 4s, - istante di tempo relativo al punto B
v0 = 0ms-1 – velocità che ha il corpo all’istante t0;
sB = 12m – posizione occupata dal corpo all’istante tB e calcolata in precedenza.
Sostituendo i valori si ottiene:
1
2
 a BC  t B  v 0  t B  s 0
2
1
12   0,75  4 2  0  4  s 0
2
1
12   0,75  16  s 0
2
12  6  s 0
sB 
12  6  s 0
s 0  6m
Il significato del valore ottenuto è il seguente: se il corpo si fosse mosso sempre di
MRUA, allora all’istante t=0s il corpo si troverebbe a 3m a destra dell’osservatore.
In definitiva l’equazione del moto nell’intervallo di tempo tBC è:
s BC 
1
 0,75  t 2  6
2
Dopo un intervallo di tempo tAC, qual è lo spazio percorso? Cioè, all’istante di
tempo tC=8s, dove si trova il corpo?
Lo spazio percorso, sAC, nei due intervalli di tempo considerati fino ad ora, è
s AC  s AB  s BC  12m  18m  30m
Quindi dopo
t AC  t AB  t BC  4s   4s   8s
5
il corpo si è spostato di
s AC  30m
Questo numero ha anche il seguente significato: all’istante di tempo
t C  8s
il corpo si trova a 30m dall’osservatore. Infatti sostituendo:
t C  8s
nell’equazione
sB 
1
 0,75  t 2  6
2
si ha
sB 
1
 0,75  8 2  6  24  6  30m
2
Sintesi dei risultati segmento [BC]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[BC], sono
a) l’accelerazione vale: aBC = 0,75ms-2, ed il moto è uniformemente accelerato;
b) lo spazio percorso: sBC = 18m;
b) l’equazione del moto relativa alla velocità è:
v BC  0,75  t
c) l’equazione del moto relativa alla posizione:
s BC 
6
1
 0,75  t 2  6
2
3) Segmento [CD]
Nell’intervallo di tempo:
t CD  t D  t C  (10s)  (8s)  2s
la velocità passa, in modo uniforme, da un valore iniziale
v C  6m  s 1
ad un valore finale
v D  9m  s 1
La variazione di velocità, vCD, è uniforme, cioè varia costantemente, poiché la
linea congiunge i due punti C e D è un segmento. Nell’intervallo di tempo tCD il corpo
accelera con un’accelerazione, aCD, pari a:
v CD v D  v C
9m  s 1  6m  s 1
3m  s 1
a CD 



 1,5m  s 2
10s  8s 
t CD
tD  tC
2s

 

Calcolo dello spazio percorso [CD]
Graficamente lo spazio percorso nell’intervallo di tempo tCD si calcola misurando
l’area della porzione di piano che si trova sotto il segmento [CD].
L’area da calcolare è quella di un
trapezio, dove le basi sono le velocità
iniziale, vC, e finale, vD, e l’altezza è
l’intervallo di tempo tCD. Quindi:
s CD 
s CD 
v C  v D  t CD
2
 9m  s 1  2s 
 15m
2
6m  s  
1

Calcolo dell’equazione del moto relativa alla velocità [CD]
Dal momento che il moto del corpo è rappresentato da un segmento, l’equazione
del moto avrà la stessa forma dell’equazione di una retta:
v CD  a CD  t  v 0
dove:
vCD = velocità del corpo ad ogni istante dell’intervallo di tempo tCD;
aCD = accelerazione nell’intervallo di tempo tCD, il cui valore è: aCD=1,5ms-2;
t = generico istante di tempo;
v0 = velocità che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre di un
Moto Rettilineo Uniformemente Accelerato (MRUA). Il valore di tale velocità deve
essere calcolato.
Il metodo di calcolo di v0 è identico a quello effettuato nel caso precedente. Della retta
passante per i punti C e D si conoscono le coordinate sia di C, [C(8s, 6ms-1)] sia di D
[D(10s, 9ms-1)]. Pertanto, sostituendo le coordinate di uno dei due punti nell’equazione
della velocità, si trova il valore di v0. Sostituendo le coordinate di C si ottiene:
7
v CD  a CD  t  v 0
6  1,5  8  v 0 ,
v C  a CD  t C  v 0
6  12  v 0
v 0  6m  s 1
Quindi l’equazione del moto relativa alla velocità è:
v CD  1,5  t  6
Calcolo dell’equazione del moto relativa alla posizione [CD]
L’equazione del moto rettilineo uniformemente accelerato relativa alla posizione,
nel caso generale, è:
s CD 
1
 a CD  t 2  v 0  t  s 0
2
dove.
sCD = posizione del corpo ad ogni istante dell’intervallo di tempo tCD;
aCD = accelerazione nell’intervallo di tempo tCD, il cui valore è: aCD=1,5ms-2;
t = generico istante di tempo;
v0 = velocità del corpo avrebbe all’istante t0 se si muovesse sempre di MRUA,
(v0= -6ms-1);
s0 = posizione che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre
di MRUA. Il valore di tale posizione deve essere calcolato.
Il metodo del calcolo della posizione s0 è simile a quello effettuato per il calcolo della
velocità v0. Si prende in considerazione il punto C, si nota che i parametri da introdurre
nell’equazione sono:
tC = 8s, - istante di tempo relativo al punto C
v0 = -6ms-1 – velocità che ha il corpo all’istante t0;
sC = 30m – posizione occupata dal corpo all’istante tC e calcolata in precedenza.
Sostituendo i valori si ottiene:
1
2
 a CD  t C  v 0  t C  s 0
2
1
30   1,5  8 2  6  8  s 0
2
1
30   1,5  64  48  s 0
2
30  48  48  s 0
sC 
30  s 0
s 0  30m
Il significato del valore ottenuto è il seguente: se il corpo si fosse mosso sempre di
MRUA, allora all’istante t=0s il corpo si troverebbe a 30m a destra dell’osservatore.
In definitiva l’equazione del moto nell’intervallo di tempo tCD è:
s CD 
1
 1,5  t 2  6  t  30
2
Dopo un intervallo di tempo tAD, qual è lo spazio percorso? Cioè, all’istante di
tempo tD=8s, dove si trova il corpo?
Lo spazio percorso, sAD, nei tre intervalli di tempo considerati fino ad ora, è
8
s AD  s AB  s BC  s CD  12m  18m  15m  45m
Quindi dopo
t AD  t AB  t BC  t CD  4s   4s   2s   10s
il corpo si è spostato di
s AD  45m
Questo numero ha anche il seguente significato: all’istante di tempo
t D  10s
il corpo si trova a 45m dall’osservatore. Infatti sostituendo:
t D  10s
nell’equazione
sC 
1
 1,5  t 2  6  t  30
2
si ha
sC 
1
 1,5  10 2  6  10  30  45m
2
Sintesi dei risultati segmento [CD]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[CD], sono
a) l’accelerazione vale: aCD = 1,5ms-2, ed il moto è uniformemente accelerato;
b) lo spazio percorso: sCD = 18m;
b) l’equazione del moto relativa alla velocità è:
v CD  1,5  t  6
c) l’equazione del moto relativa alla posizione:
s CD 
1
 1,5  t 2  6  t  30
2
9
4) Segmento [DE]
Nell’intervallo di tempo:
t DE  t E  t D  (14s)  (10s)  4s
la velocità passa, in modo uniforme, da un valore iniziale
v D  9m  s 1
ad un valore finale
v E  0m  s 1
La variazione di velocità, vDE, è uniforme, cioè varia costantemente, poiché la
linea congiunge i due punti D e E è un segmento. Nell’intervallo di tempo tCD il corpo
accelera con un’accelerazione, aCD, pari a:
v DE v E  v D
0m  s 1  9m  s 1
 9m  s 1
a DE 



 2,25m  s 2
14s  10s 
t DE
tE  tD
4s
Come si può notare il valore dell’accelerazione è negativa, ciò è dovuto al fatto che
la velocità sta diminuendo. Poiché la velocità, nell’intervallo tDE, è positiva, significa
che il corpo continua a muoversi in avanti. Inoltre si osserva che all’istante tE=14s il
corpo si ferma, poiché la velocità, vE, è nulla.
Per il segmento [DE] si ripetono i calcoli effettuati nei casi precedenti. Tali calcoli
saranno omessi, però saranno forniti i risultati finali, in modo che i valori possano trovati
in modo autonomo.

 

Calcolo dello spazio percorso nel segmento [DE]
Dal grafico si calcola lo spazio percorso nell’intervallo di tempo tDE. L’area sotto
il segmento è un triangolo rettangolo. Lo spazio percorso nell’intervallo di tempo è:
t DE  4s
Lo spazio percorso è
s DE  18m
Calcolo dell’equazione del moto relativa alla velocità nel segmento [DE]
Partendo dall’equazione:
v DE  a DE  t  v 0
v DE  2,25  t  v 0
e prendendo come riferimento il punto D, con coordinate D(10s, 9m), si calcola il valore
di v0. Sostituendo le coordinate di C si ottiene:
9  2,25  10  v 0 ,
v 0  31,5m  s 1
Quindi l’equazione del moto relativa alla velocità è:
v DE  2,25  t  31,5
10
Calcolo dell’equazione del moto relativa alla posizione [DE]
L’equazione del moto rettilineo uniformemente accelerato relativa alla posizione,
nel caso generale, è:
s DE 
1
 a DE  t 2  v 0  t  s 0
2
dove.
sDE = posizione del corpo ad ogni istante dell’intervallo di tempo tDE;
aDE = accelerazione nell’intervallo di tempo tDE, il cui valore è: aDE=-2,25ms-2;
t = generico istante di tempo;
v0 = velocità del corpo avrebbe all’istante t0 se si muovesse sempre di MRUA,
(v0= 31,5ms-1);
s0 = posizione che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre
di MRUA. Il valore di tale posizione deve essere calcolato.
Il metodo del calcolo della posizione s0 è simile a quello effettuato per il calcolo della
velocità v0. Si prende in considerazione il punto D, si nota che i parametri da introdurre
nell’equazione sono:
tD = 10s, - istante di tempo relativo al punto D
v0 = 31,5ms-1 – velocità che ha il corpo all’istante t0;
sD = 45m – posizione occupata dal corpo all’istante tD e calcolata in precedenza.
Sostituendo i valori si ottiene:
s DE 
45 
1
 a DE  t 2  v 0  t  s 0
2
1
  2,25 10 2  31,5  10  s 0
2
s 0  157,5m
Il significato del valore ottenuto è il seguente: se il corpo si fosse mosso sempre di
MRUA, allora all’istante t=0s il corpo si troverebbe a 30m a destra dell’osservatore.
In definitiva l’equazione del moto nell’intervallo di tempo tDE è:
1
s D    2,25  t 2  31,5  t  157,5
2
Dopo un intervallo di tempo tAE, qual è lo spazio percorso? Cioè, all’istante di
tempo tE=14s, dove si trova il corpo?
Lo spazio percorso, sAE, nei quattro intervalli di tempo considerati fino ad ora, è
s AE  s AB  s BC  s CD  s DE  12m  18m  15m  18m  63m
Quindi dopo
t AE  t AB  t BC  t CD  t DE  4s   4s   2s   4s   14s
il corpo si è spostato di
s AD  63m
Questo numero ha anche il seguente significato: all’istante di tempo
t E  14s
il corpo si trova a 63m dall’osservatore. Infatti sostituendo:
t E  14s
nell’equazione
1
s DE    2,25  t 2  31,5  t  157,5
2
11
si ha
1
s D    2,25  14 2  31,5  14  157,5  63m
2
Sintesi dei risultati segmento [DE]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[DE], sono
a) l’accelerazione vale: aCD = -2,25ms-2, ed il moto è uniformemente accelerato;
b) lo spazio percorso: sDE = 18m;
b) l’equazione del moto relativa alla velocità è:
v DE  2,25  t  31,5
c) l’equazione del moto relativa alla posizione:
1
s DE    2,25  t 2  31,5  t  157,5
2
12
5) Segmento [EF]
Nell’intervallo di tempo:
t EF  t F  t E  (16s)  (14s)  2s
la velocità non cambia e vale:
v E  v F  0m  s 1
quindi il corpo è fermo. Ovviamente
l’accelerazione aEF è nulla.
a EF  0 m  s 2
Il corpo si mantiene nella posizione
costante:
s E  s F  63 m
13
6) Segmento [FG]
Nell’intervallo di tempo:
t FG  t G  t F  (19s)  (16s)  3s
la velocità passa, in modo uniforme, da un valore iniziale
v F  0m  s 1
ad un valore finale
v G  2m  s 1
La variazione di velocità, vFG, è uniforme, cioè varia costantemente, poiché la
linea congiunge i due punti F e G è un segmento. Nell’intervallo di tempo tFG il corpo
accelera con un’accelerazione, aFG, pari a:
v FG v G  v F
 2m  s 1  0m  s 1
 2m  s 1
a FG 



 0,67m  s 2
19s  16s
t FG
tG  tF
3s
Come si può notare il valore dell’accelerazione è negativa, ciò è dovuto al fatto che
la velocità sta diminuendo. La velocità, nell’intervallo tFG, è negativa, ed il corpo si
muove all’indietro.
Per il segmento [FG] si ripetono i calcoli effettuati nei casi precedenti.

 

Calcolo dello spazio percorso nel segmento [FG]
Dal grafico si calcola lo spazio percorso nell’intervallo di tempo tFG. L’area sotto
il segmento è un triangolo
rettangolo. Lo spazio percorso
nell’intervallo di tempo
t FG  3s
lo spazio percorso è
s FG  3m
Il valore è negativo poiché il
corpo sta tornando indietro.
Calcolo dell’equazione del moto relativa alla velocità [FG]
Nell’intervallo di tempo t FG  3s , il corpo continua a muoversi di moto
uniformemente vario. L’equazione del moto è:
v FG  a FG  t  v 0
dove:
vFG = velocità del corpo ad ogni istante dell’intervallo di tempo tFG;
aFG = accelerazione nell’intervallo di tempo tFG, il cui valore è: aFG-0,67ms-2;
t = generico istante di tempo;
v0 = velocità che avrebbe il corpo all’istante iniziale t=0s, il valore viene calcolato con
lo stesso procedimento visto in precedenza.
Si prende come punto di riferimento il punto F, le cui coordinate sono: F(16s, 0ms-1).
Sostituendo tali valori nell’equazione della velocità
14
v FG  a FG  t  v 0
si ottiene:
v F  a FG  t F  v 0
0  0,67  16  v 0
v 0  10,67m  s 1
Quindi l’equazione del moto relativa alla velocità è:
v FG  0,67  t  10,67
Calcolo dell’equazione del moto relativa alla posizione [FG]
L’equazione del moto rettilineo uniformemente accelerato relativa alla posizione,
nel caso generale, è:
s FG 
1
 a FG  t 2  v 0  t  s 0
2
dove.
SFG = posizione del corpo ad ogni istante dell’intervallo di tempo tFG;
aFG = accelerazione nell’intervallo di tempo tFG, il cui valore è: aFG-0,67ms-2;
t = generico istante di tempo;
v0 = velocità del corpo avrebbe all’istante t0 se si muovesse sempre di MRUA,
(v0 10,72ms-1);
s0 = posizione che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre
di moto uniformemente accelerato. Il suo valore si calcola come nei casi
precedenti.
Si prende come riferimento il punto F le cui coordinate sono: , si nota che i
parametri da introdurre nell’equazione sono: F(16s, 0ms-1).
All’istante tF=16s, il corpo si trova ad una distanza dall’osservatore pari a:
sF=63m.
Sostituendo i valori nell’equazione relativa allo spazio:si ottiene:
sF 
1
2
 a FG  t F  v 0  t F  s 0
2
si ottiene:
63 
1
  0,67   16 2  10,67  16  s 0
2
s 0  22,33m
L’equazione del moto nell’intervallo di tempo tFG è:
1
s FG    0,67  t 2  10,67  t  22,33
2
Dopo un intervallo di tempo tAG=19s, lo spazio percorso, sAG, nei sei intervalli
è:
s AG
s AG  s AB  s BC  s CD  s DE  s EF  s FG
 12m  18m  15m  18m  0m   3m  60m
15
Sintesi dei risultati segmento [FG]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[FG], sono
2
a) l’accelerazione vale: a FG   m  s  2  0,67m  s  2 ;
3
b) lo spazio percorso: sFG = -3m;
b) l’equazione del moto relativa alla velocità è:
2
32
v FG    t 
3
3
v FG  0,67  t  10,67
c) l’equazione del moto relativa alla posizione:
2
32
67
s FG    t 2 
t 
3
3
3
1
s FG    0,67  t 2  10,67  t  22,33
2
16
(coefficienti esatti)
(coefficienti approssimati)
(coefficienti esatti)
(coefficienti approssimati)
7) Segmento [GH]
Nell’intervallo di tempo:
t GH  t H  t G  (24s)  (19s)  5s
la velocità passa, in modo uniforme, da un valore iniziale
v G  2m  s 1
ad un valore finale
v H  7m  s 1
La variazione di velocità è uniforme, e nell’intervallo di tempo tGH il corpo
accelera con un’accelerazione, aGH, pari a:
v GH v H  v G
7m  s 1   2m  s 1
9m  s 1
a GH 



 1,8m  s 2
24s  19s
t GH
tH  tG
5s

 

Calcolo dello spazio percorso nel segmento [GH]
L’analisi del grafico relativo al segmento [GH] richiede qualche osservazione.
Il segmento interseca l’asse delle ascisse del tempo nel punto K, le cui coordinate
sono: K(20,11s, 0ms-1).
L’accelerazione è positiva (aGH=1,8ms-2), però la velocità è negativa dall’istante
tG=19s fino all’istante tK=20,11s. In questo intervallo di tempo
t GK  t K  t G  20,11s   19s   1,11s
il
corpo
continua
a
muoversi all’indietro, fino a
fermarsi all’istante tK.
Graficamente lo spazio
percorso nell’intervallo tGK si
calcola misurando l’area del
triangolo sotto il segmento [GK].
Il valore è:
s GK  1,11m
Dall’istante tK=20,11s in
poi, la velocità diventa positiva
ed il corpo inverte il moto e si muove in avanti, sempre con la stessa accelerazione aGH.
Lo spazio percorso nell’intervallo di tempo
t KH  t H  t K  24s  20,11s  3,86s
Dal grafico si calcola lo spazio percorso nell’intervallo di tempo tKH, il cui valore
è:
s GK  13.61m
Calcolo dell’equazione del moto relativa alla velocità [GH]
Nell’intervallo di tempo t GH  6s , il corpo continua a muoversi di moto
uniformemente vario. L’equazione del moto è:
v GH  a GH  t  v 0
dove:
vGH = velocità del corpo ad ogni istante dell’intervallo di tempo tGH;
aGH = accelerazione nell’intervallo di tempo tGH, il cui valore è: aGH=1,8ms-2;
17
t = generico istante di tempo;
v0 = velocità che avrebbe il corpo all’istante iniziale t=0s, il valore viene calcolato con
lo stesso procedimento visto in precedenza.
Si prende come punto di riferimento il punto G, le cui coordinate sono: G(-2s, 19ms-1).
Sostituendo tali valori nell’equazione della velocità
v GH  a GH  t  v 0
si ottiene:
v G  a GH  t F  v 0
 2  1,8  19  v 0
v 0  36,2m  s 1
Quindi l’equazione del moto relativa alla velocità è:
v GH  1,8  t  36,2
Calcolo dell’equazione del moto relativa alla posizione [GH]
L’equazione del moto rettilineo uniformemente accelerato relativa alla posizione,
nel caso generale, è:
s GH 
1
 a GH  t 2  v 0  t  s 0
2
dove.
SGH = posizione del corpo ad ogni istante dell’intervallo di tempo tGH;
aGH = accelerazione nell’intervallo di tempo tGH, il cui valore è: aGH=1,8ms-2;
t = generico istante di tempo;
v0 = velocità del corpo avrebbe all’istante t0 se si muovesse sempre di MRUA,
(v0= -36,2ms-1);
s0 = posizione che avrebbe il corpo all’istante iniziale t=0s, se si muovesse sempre
di moto uniformemente accelerato. Il suo valore si calcola come nei casi
precedenti.
Si prende come riferimento il punto G le cui coordinate sono: G(19s, -2ms-1).
All’istante tF=19s, il corpo si trova ad una distanza dall’osservatore pari a:
sG=60m.
Sostituendo i valori nell’equazione relativa allo spazio:si ottiene:
sG 
1
2
 a GH  t G  v 0  t H  s 0
2
si ottiene:
60 
1
 1,8  19 2  36,2  19  s 0
2
s 0  422,9m
L’equazione del moto nell’intervallo di tempo tFG è:
s GH 
1
 1,8  t 2  36,2  t  422,9
2
Dopo un intervallo di tempo tAH=24s, lo spazio percorso, sAH, negli otto
intervalli è:
s AG  s AB  s BC  s CD  s DE  s EF  s FG  s GK  s KH
s AG  12m  18m  15m  18m  0m   3m   1,11m  13,61m  72,5m
18
Sintesi dei risultati segmento [GH]:
In sintesi, i risultati, che si ottengono osservando il grafico relativo al segmento
[GH], sono
a) l’accelerazione vale: a GH  1,8m  s 2 ;
b) lo spazio percorso: sFG = (-1,11m)+(13,61m)=12,5m;
b) l’equazione del moto relativa alla velocità è:
v GH  1,8  t  36,2
c) l’equazione del moto relativa alla posizione:
s GH 
1
 1,8  t 2  36,2  t  422,9
2
19
Grafico spazio- tempo
L’analisi del moto del corpo è avvenuta partendo da grafico velocità – tempo. Dai calcoli
effettuati si può passare al grafico spazio tempo. Il grafico di sotto riproduce il moto lungo una retta
del corpo. Il grafico è formato da varie parti di seguito elencate:
[AB]: l’equazione è una retta;
[BC]: l’equazione è una parabola con la concavità rivolta verso l’alto;
[CD]: l’equazione è una parabola con la concavità rivolta verso l’alto;
[DE]: l’equazione è una parabola con la concavità rivolta verso il basso;
[EF]: tratto orizzontale di retta;
[FG]: l’equazione è una parabola con la concavità rivolta verso il basso;
[GH]: l’equazione è una parabola con la concavità rivolta verso l’alto.
20