L` AREA DI POLIGONI REGOLARI

1
L’ AREA DI POLIGONI REGOLARI
Ci proponiamo in questo foglio di vedere un applicazione delle funzioni trigonometriche per calcolare l’area di un
poligono regolare qualsiasi. Non è richiesta nessuna conoscenza che vada al di la di quanto fatto in un un corso di
trigonometria delle scuole superiori.
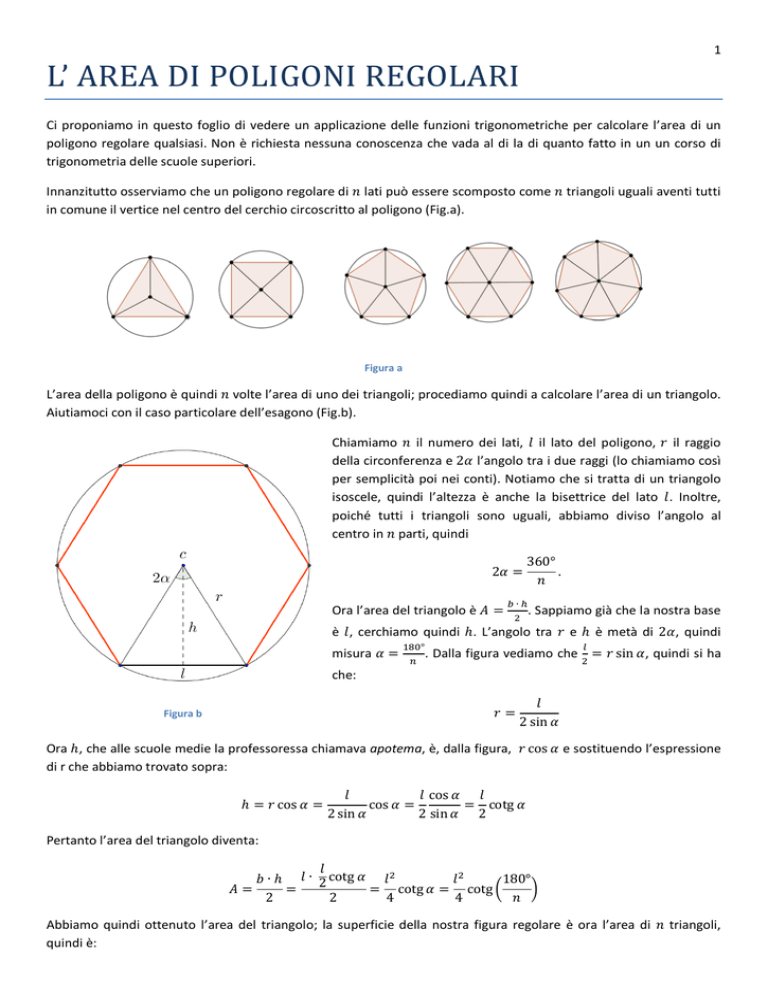
Innanzitutto osserviamo che un poligono regolare di 𝑛 lati può essere scomposto come 𝑛 triangoli uguali aventi tutti
in comune il vertice nel centro del cerchio circoscritto al poligono (Fig.a).
Figura a
L’area della poligono è quindi 𝑛 volte l’area di uno dei triangoli; procediamo quindi a calcolare l’area di un triangolo.
Aiutiamoci con il caso particolare dell’esagono (Fig.b).
Chiamiamo 𝑛 il numero dei lati, 𝑙 il lato del poligono, 𝑟 il raggio
della circonferenza e 2𝛼 l’angolo tra i due raggi (lo chiamiamo così
per semplicità poi nei conti). Notiamo che si tratta di un triangolo
isoscele, quindi l’altezza è anche la bisettrice del lato 𝑙. Inoltre,
poiché tutti i triangoli sono uguali, abbiamo diviso l’angolo al
centro in 𝑛 parti, quindi
2𝛼 =
Ora l’area del triangolo è 𝐴 =
360°
.
𝑛
𝑏∙ℎ
.
2
Sappiamo già che la nostra base
è 𝑙, cerchiamo quindi ℎ. L’angolo tra 𝑟 e ℎ è metà di 2𝛼, quindi
misura 𝛼 =
che:
180°
.
𝑛
𝑟=
Figura b
𝑙
2
Dalla figura vediamo che = 𝑟 sin 𝛼, quindi si ha
𝑙
2 sin 𝛼
Ora ℎ, che alle scuole medie la professoressa chiamava apotema, è, dalla figura, 𝑟 cos 𝛼 e sostituendo l’espressione
di r che abbiamo trovato sopra:
ℎ = 𝑟 cos 𝛼 =
Pertanto l’area del triangolo diventa:
𝑙
𝑙 cos 𝛼 𝑙
cos 𝛼 =
= cotg 𝛼
2 sin 𝛼
2 sin 𝛼 2
𝑙
𝑏 ∙ ℎ 𝑙 ∙ 2 cotg 𝛼 𝑙2
𝑙2
180°
𝐴=
=
= cotg 𝛼 = cotg �
�
2
𝑛
2
4
4
Abbiamo quindi ottenuto l’area del triangolo; la superficie della nostra figura regolare è ora l’area di 𝑛 triangoli,
quindi è:
𝑙2
180°
𝑛
180°
𝐴𝑛 = 𝑛 cotg �
� = 𝑙2 � cotg �
��
𝑛
4
𝑛
4
2
Si ha dunque che l’area di un poligono regolare di 𝑛 lati di lunghezza 𝑙 è l’area di un quadrato (𝑙 2 ) moltiplicata per un
fattore che dipende solo da 𝑛 che chiameremo, rubando sempre i nomi dalle scuole medie, numero fisso (𝑓):
Vediamo quanto vale 𝑓 per alcuni numeri:
•
•
•
𝑛 = 3:
𝑛 = 4:
𝑛 = 6:
𝑓=
𝑛
180°
cotg �
�
4
𝑛
3
180°
3
3 √3 √3
cotg �
� = cotg(60°) = ∙
=
≈ 0.43
4
3
4
4 3
4
4
180°
cotg �
� = 1 ∙ cotg(45°) = 1 ∙ 1 = 1
4
4
6
180°
3
3
3√3
cotg �
� = cotg(30°) = ∙ √3 =
≈ 1.72
4
6
2
2
2
APPLICAZIONE: (Il teorema di Pitagora).
Sappiamo tutti che se 𝑐1 e 𝑐2 sono i cateti di un triangolo rettangolo e 𝑖𝑝 è l’ipotenusa, il teorema di Pitagora ci dice
che ‘In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è sempre equivalente alla somma dei quadrati
costruiti sui cateti’:
Moltiplichiamo da entrambe le parti per 𝑓:
𝑖𝑝 2 = (𝑐1 )2 + (𝑐2 )2
𝑓 ∙ 𝑖𝑝2 = 𝑓[(𝑐1 )2 + (𝑐2 )2 ]
𝑓 ∙ 𝑖𝑝 2 = 𝑓(𝑐1 )2 + 𝑓(𝑐2 )2
Interpretiamo l’ultimo risultato: stiamo moltiplicando le lunghezze dei tre lati al quadrato per un numero 𝑓. Ma
questo equivale, per quanto abbiamo detto prima, a calcolare l’area non di un quadrato, ma di un poligono regolare.
Quindi abbiamo fatto vedere che ‘In ogni triangolo rettangolo il poligono regolare costruito sull'ipotenusa è sempre
equivalente alla somma dei poligoni regolari costruiti sui cateti’. Mettiamo ora alcune immagini di quanto abbiamo
ottenuto. I poligoni sui lati sono stati suddivisi, per dare un'altra dimostrazione di questo fatto che noi abbiamo
mostrato per via puramente algebrica.
PENTAGONO:
3
ESAGONO:
ETTAGONO: