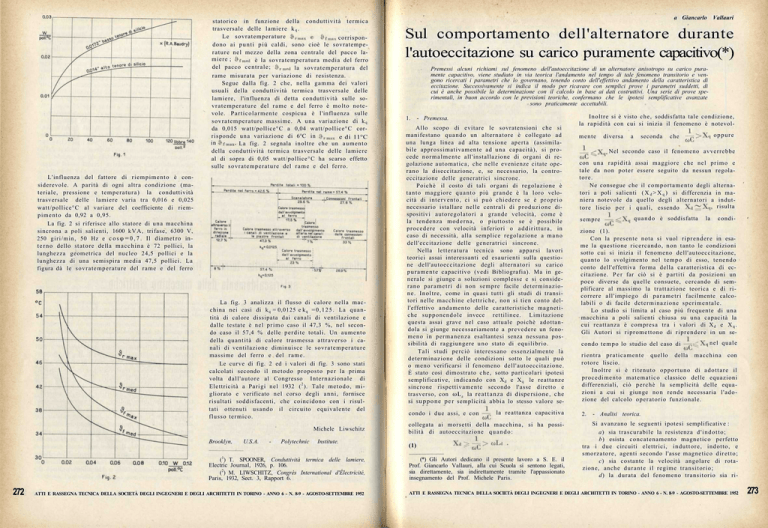
statorico in funzione della conduttività termica
trasversale delle lamiere k q .
Le s o v r a t e m p e r a t u r e
corrispondono ai p u n t i p i ù caldi, sono cioè le sovratemper a t u r e nel mezzo della zona centrale del pacco lamiere ;
è la sovratemperatura media del ferro
del pacco c e n t r a l e ;
la s o v r a t e m p e r a t u r a del
r a m e misurata p e r variazione di resistenza.
Segue dalla fig. 2 che, nella gamma dei valori
usuali della conduttività termica trasversale delle
lamiere, l'influenza di detta conduttività sulle sov r a t e m p e r a t u r e del r a m e e del ferro è molto notevole. P a r t i c o l a r m e n t e cospicua è l'influenza sulle
s o v r a t e m p e r a t u r e massime. A u n a variazione di k q
da 0,015 watt/pollice°C a 0,04 watt/pollice°C corrisponde u n a variazione di 6°C in
e di 11°C
in
La fig. 2 segnala inoltre che un a u m e n t o
della conduttività termica trasversale delle lamiere
al di sopra di 0,05 watt/pollice°C ha scarso effetto
sulle s o v r a t e m p e r a t u r e del r a m e e del ferro.
L'influenza del fattore di r i e m p i m e n t o è considerevole. A parità di ogni altra condizione (materiale, pressione e t e m p e r a t u r a ) la conduttività
trasversale delle lamiere varia tra 0,016 e 0,025
watt/pollice°C al variare del coefficiente di riemp i m e n t o da 0,92 a 0,95.
La fig. 2 si riferisce allo statore di u n a macchina
sincrona a poli salienti, 1600 k V A , trifase, 6300 V,
250 g i r i / m i n , 50 Hz e c o s φ = 0 , 7 . Il d i a m e t r o int e r n o dello statore della m a c c h i n a è 72 pollici, la
lunghezza geometrica del nucleo 24,5 pollici e la
lunghezza di u n a semispira m e d i a 47,5 pollici. La
figura dà le s o v r a t e m p e r a t u r e del r a m e e del ferro
La fig. 3 analizza il flusso di calore nella macchina nei casi di k q = 0,0125 e k q = 0 , 1 2 5 . La quantità di calore dissipata dai canali di ventilazione e
dalle testate è nel p r i m o caso il 47,3 %, nel secondo caso il 57,4 % delle p e r d i t e totali. Un a u m e n t o
della q u a n t i t à di calore trasmessa attraverso i canali di ventilazione diminuisce le s o v r a t e m p e r a t u r e
massime del ferro e del r a m e .
Le curve di fig. 2 ed i valori di fig. 3 sono stati
calcolati secondo il m e t o d o proposto p e r la prima
volta d a l l ' a u t o r e al Congresso Internazionale di
Elettricità a Parigi nel 1932 ( 2 ). Tale m e t o d o , migliorato e verificato nel corso degli a n n i , fornisce
risultati soddisfacenti, che coincidono con i risultati ottenuti u s a n d o il circuito equivalente del
flusso termico.
Michele Liwschitz
Brooklyn,
U.S.A.
-
Polytechnic
Institute.
(1) T. SPOONER, Conduttività termica delle lamiere,
Electric Journal, 1926, p. 106.
(2) M. LIWSCHITZ, Congrès International d'Électricité,
Paris, 1932, Sect. 3, Rapport 6.
272
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
a Giancarlo Vallauri
Sul comportamento dell'alternatore durante
l'autoeccitazione su carico puramente capacitivo(*)
Premessi alcuni richiami sul fenomeno dell'autoeccitazione di un alternatore anisotropo su carico puramente capacitivo, viene studiato in via teorica l'andamento nel tempo di tale fenomeno transitorio e vengono ricercati i parametri che lo governano, tenendo conto dell'effettivo andamento della caratteristica di
eccitazione. Successivamente si indica il modo per ricavare con semplici prove i parametri suddetti, di
cui è anche possibile la determinazione con il calcolo in base ai dati costruttivi. Una serie di prove sperimentali, in buon accordo con le previsioni teoriche, confermano che le ipotesi semplificative avanzate
sono praticamente accettabili.
1.
- Premessa.
Allo scopo di evitare le sovratensioni che si
manifestano q u a n d o un alternatore è collegato ad
una lunga linea ad alta tensione aperta (assimilabile approssimativamente ad u n a capacità), si p r o cede n o r m a l m e n t e all'installazione di organi di regolazione automatica, che nelle evenienze citate oper a n o la diseccitazione, e, se necessario, la controeccitazione delle generatrici sincrone.
Poichè il costo di tali organi di regolazione è
t a n t o maggiore q u a n t o più g r a n d e è la loro velocità di intervento, ci si p u ò chiedere se è p r o p r i o
necessario istallare nelle centrali di p r o d u z i o n e dispositivi autoregolatori a grande velocità, come è
la tendenza m o d e r n a , o piuttosto se è possibile
procedere con velocità inferiori o a d d i r i t t u r a , in
caso di necessità, alla semplice regolazione a m a n o
dell'eccitazione delle generatrici sincrone.
Nella letteratura tecnica sono apparsi lavori
teorici assai interessanti ed esaurienti sulla questione dell'autoeccitazione degli alternatori su carico
p u r a m e n t e capacitivo (vedi Bibliografia). Ma in generale si giunge a soluzioni complesse e si considerano p a r a m e t r i di non sempre facile determinazion e . I n o l t r e , come in quasi t u t t i gli studi di transitori nelle macchine elettriche, non si tien conto dell'effettivo a n d a m e n t o delle caratteristiche magnetiche supponendole invece rettilinee. Limitazione
questa assai grave nel caso attuale poichè adottandola si giunge necessariamente a prevedere un fenom e n o in p e r m a n e n z a esaltantesi senza nessuna possibilità di raggiungere u n o stato di equilibrio.
Tali studi perciò interessano essenzialmente la
determinazione delle condizioni sotto le quali p u ò
o meno verificarsi il fenomeno dell'autoeccitazione.
È stato così dimostrato che, sotto particolari ipotesi
semplificative, indicando con X d e X q le reattanze
sincrone rispettivamente secondo l'asse diretto e
trasverso, con ωL d la reattanza di dispersione, che
si s u p p o n e p e r semplicità abbia lo stesso valore secondo i due assi, e con
la reattanza capacitiva
collegata ai morsetti della macchina, si ha possibilità di autoeccitazione q u a n d o :
(1)
(*) Gli Autori dedicano il presente lavoro a S. E. il
Prof. Giancarlo Vallauri, alla cui Scuola si sentono legati,
sia direttamente, sia indirettamente tramite l'appassionato
insegnamento del Prof. Michele Paris.
Inoltre si è visto che, soddisfatta tale condizione,
la r a p i d i t à con cui si inizia il fenomeno è notevolmente
diversa
a
seconda
oppure
che
Nel secondo caso il fenomeno avverrebbe
con u n a r a p i d i t à assai maggiore che nel p r i m o e
tale da non p o t e r essere seguito da nessun regolatore.
Ne consegue che il c o m p o r t a m e n t o degli alternatori a poli salienti ( X d > X q ) si differenzia in maniera notevole da quello degli alternatori a indutrisulta
tore liscio p e r i quali, essendo
sempre
q u a n d o è soddisfatta
la
condi-
zione (1).
Con la presente nota si vuol r i p r e n d e r e in esame la questione ricercando, n o n tanto le condizioni
sotto cui si inizia il fenomeno dell'autoeccitazione,
q u a n t o lo svolgimento nel t e m p o di esso, t e n e n d o
conto dell'effettiva forma della caratteristica di eccitazione. P e r far ciò si è p a r t i t i da posizioni un
poco diverse da quelle consuete, cercando di semplificare al massimo la trattazione teorica e di ricorrere all'impiego di p a r a m e t r i facilmente calcolabili o di facile determinazione sperimentale.
Lo studio si limita al caso più frequente di u n a
macchina a poli salienti chiusa su una capacità la
cui reattanza è compresa tra i valori di X d e X q .
Gli Autori si r i p r o m e t t o n o di r i p r e n d e r e in un secondo t e m p o lo studio del caso di
nel quale
rientra praticamente quello della macchina con
rotore liscio.
Inoltre si è r i t e n u t o o p p o r t u n o di a d o t t a r e il
p r o c e d i m e n t o m a t e m a t i c o classico delle equazioni
differenziali, ciò p e r c h è la semplicità delle equazioni a cui si giunge n o n r e n d e necessaria l'adozione del calcolo o p e r a t o r i o funzionale.
2.
- Analisi teorica.
Si avanzano le seguenti ipotesi semplificative :
a) sia trascurabile la resistenza d ' i n d o t t o ;
b) esista concatenamento magnetico perfetto
tra i due circuiti elettrici, i n d u t t o r e , i n d o t t o , e
smorzatore, agenti secondo l'asse magnetico d i r e t t o ;
c) sia costante la velocità angolare di rotazione, anche d u r a n t e il regime t r a n s i t o r i o ;
d) la d u r a t a del fenomeno transitorio sia ri-
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
273
Ne risulta che si verifica o no il fenomeno dell'autoeccitazione a seconda che la caratteristica di
carico capacitivo è inferiore o superiore alla retta
tangente alla p a r t e iniziale della caratteristica di
eccitazione. I due casi sono separati dalla coincidenza delle due rette, cui corrisponde un particolare valore della reattanza capacitiva di carico che
indicheremo come « reattanza capacitiva limite » e
che, riferendosi a q u a n t o detto nella premessa, coincide in valore assoluto con la reattanza sincrona diretta.
Nel caso in cui si verifica l'autoeccitazione, si
p u ò ricavare il valore della f.e.m. E 2 a regime dal
p u n t o di incontro delle d u e caratteristiche ( p u n t o
P di figura 1). La tensione ai morsetti V 2 si p o t r à
ottenere sommando ad E 2 la caduta dovuta alla
reattanza di dispersione ωL d p e r la c o r r e n t e I 2 ,
ascissa del p u n t o P, o p p u r e più semplicemente mediante la relazione
(3)
Fig. 1. - Caratteristica di eccitazione dell'alternatore su cui
si sono eseguite le prove ed esempio di caratteristica di carico capacitivo.
levante in confronto alla d u r a t a del p e r i o d o delle
grandezze sinoidali;
e) sia trascurabile l'effetto derivante dalla
presenza di c a m p i a r m o n i c i .
Si ricorda inoltre come la caratteristica di eccitazione rotorica e 2 = f 1 (i 1 ) (figura 1), che si ricava
dalla consueta prova a vuoto degli a l t e r n a t o r i , p u ò
r a p p r e s e n t a r e anche la caratteristica di eccitazione
statorica e 2 = f 2 (i 2 ) dovuta ad una corrente i 2 nel
circuito indotto d i r e t t o ; è sufficiente p e r questo rip o r t a r e la corrente i 2 al n u m e r o di spire dell'induttore moltiplicandone l'intensità p e r il « coefficiente
di reazione » K 2 ricavabile dal triangolo di P o t i e r .
Infatti si p u ò definire K 2 come r a p p o r t o fra la corrente di eccitazione i 1 e la c o r r e n t e statorica i 2 , ad
essa equivalente agli effetti magnetici.
P e r l'ipotesi a), con carico p u r a m e n t e reattivo,
la corrente di indotto dell'alternatore interessa
esclusivamente il circuito diretto. Inoltre se la reattanza è capacitiva, la relazione tra la f.e.m. e 2
e la corrente i 2 è data dalla relazione
(2)
che sul p i a n o cartesiano (e 2 , i 2 ) r a p p r e s e n t a u n a
retta passante p e r l'origine (figura 1).
I n d i c a n d o tale retta col n o m e di « caratteristica
di carico capacitivo », si p u ò n o t a r e come essa, e
la caratteristica di eccitazione statorica, rappresentino due legami tra le stesse variabili; legami che
possono essere e n t r a m b i soddisfatti solo se le d u e
curve h a n n o p u n t i a comune e se tali p u n t i corrispondono a condizioni di equilibrio stabile.
274
Poichè tale tensione non viene raggiunta istant a n e a m e n t e all'atto della chiusura d e l l ' a l t e r n a t o r e
sul carico capacitivo, ci si p r o p o n e di ricercare la
funzione del t e m p o , e 2 = e 2 (t), da cui si ricava facilmente m e d i a n t e la (3) la v 2 = v 2 (t), essendosi
indicati con e 2 e v 2 rispettivamente i valori efficaci istantanei ( 1 ) della f.e.m. interna e della tensione ai morsetti della generatrice sincrona.
Oltre alle notazioni adottate si indichi ora con :
il , i2 , ig
il valore istantaneo delle correnti circolanti rispettivamente nel circuito ind u t t o r e , indotto, s m o r z a t o r e ;
i
u n a corrente fittizia che circolando
n e l l ' i n d u t t o r e p r o d u c e da sola u n a
f . m . m . pari alla f.m.m. totale sull'asse d i r e t t o ;
R1 , Rg
N1, N2, Ng
Kg
le resistenze o h m i c h e del circuito rispettivamente i n d u t t o r e e s m o r z a t o r e ;
il n u m e r o di spire equivalente (cioè
comprensivo del fattore di avvolgim e n t o e di altri eventuali coefficienti
numerici) relativo al circuito induttore, indotto, s m o r z a t o r e ;
il r a p p o r t o
di trasformazione fra
circuito smorzatore ed i n d u t t o r e ;
φ il
flusso
magnetico
risultante
secondo
l'asse d i r e t t o ;
E1
la f.e.m. continua di eccitazione.
Si ritiene o p p o r t u n o fare ricorso ad un circuito
equivalente della m a c c h i n a sincrona. In virtù dell'ipotesi di assenza di flusso magnetico secondo l'asse trasverso della macchina e d e l l ' a l t r a ipotesi relativa al perfetto c o n c a t e n a m e n t o esistente fra i
circuiti che abbracciano il flusso diretto, la macchina sincrona considerata da un osservatore solidale nella rotazione con il r o t o r e , p u ò riguardarsi
come costituita da tre circuiti elettrici come è specificato in figura 2.
Il circuito i n d u t t o r e è sottoposto in generale sia
alla f.e.m. di eccitazione E 1 sia ad u n a f.e.m.
i n d o t t a dalla variazione del flusso diretto
concatenato.
Il circuito smorzatore, che deve intendersi costituito n o n solo della gabbia smorzatrice vera e
p r o p r i a secondo l'asse magnetico diretto ma a n c h e
dai varii circuiti presenti nelle p a r t i metalliche
massicce, è soggetto alla sola
avendo posto n e l l ' u l t i m a espressione:
(5)
Poichè la f.e.m. e 2 è, per l'ipotesi di velocità di
rotazione costante, direttamente proporzionale al
flusso φ, avendo indicato con h il coefficiente di
proporzionalità (e 2 = hφ), le (4) divengono:
(6)
f.e.m.
indotta in esso dalla variazione del flusso diretto
concatenato.
P e r q u a n t o concerne il circuito statorico, si osservi come la corrente a l t e r n a t a che in esso circola
p r o d u c a n e l caso a t t u a l e u n a f.m.m. r o t a n t e che
agisce secondo l'asse d i r e t t o , in concomitanza con
la f.m.m. p r i m a r i a ; ciò, dal p u n t o di vista magnetico, equivale a dire che il circuito indotto si comp o r t a come un avvolgimento avente in ogni istante
il p r o p r i o asse orientato secondo l'asse magnetico
d i r e t t o — e q u i n d i con esso r o t a n t e — percorso da
u n a corrente continua fittizia i 2 .
D ' a l t r a p a r t e il flusso φ, e con esso la f.e.m. e 2 ,
d i p e n d o n o dalla f . m . m . totale agente secondo l'asse
diretto e q u i n d i dalla c o r r e n t e :
(7)
La relazione t r a e 2 e la corrente i è data dalla caratteristica di eccitazione, che p u ò esprimersi con
la relazione:
(8)
Affinchè in tale circuito equivalente statorico
circoli la corrente i 2 è necessario s u p p o r r e l'esistenza di u n a f.e.m. esterna continua e 2 p r o p o r zionale al flusso diretto concatenato φ ( e 2 = hφ)
nonchè la chiusura del circuito su u n a resistenza
Ricavando dalla (6) le correnti nei tre circuiti ed
introducendole nella (8), si ha in definitiva p e r e 2
l'equazione differenziale:
fittizia di valore
Alla difficoltà di risoluzione di tale e q u a z i o n e ,
dovuta al fatto che la caratteristica di eccitazione
I segni di e 2 e di
sono scelti in m o d o
che, se nel circuito statorico prevale la reattanza
capacitiva, la resistenza fittizia risulta positiva e la
corrente dovuta ad e 2 ha effetto magnetico concomitante con la corrente di eccitazione i 1 , m e n t r e
se prevale la reattanza induttiva, la resistenza fittizia è negativa e la corrente dovuta ad e 2 ha effetto
smagnetizzante; ciò è in accordo con i fenomeni di
reazione d ' i n d o t t o nel caso di carico reattivo. Si
p u ò r i t e n e r e che tale circuito equivalente statorico,
la cui adozione è p i e n a m e n t e giustificata nella condizione di regime, valga a n c h e d u r a n t e il transit o r i o , p e r cui in esso in tali circostanze, oltre alla
f.e.m. e 2 , agirà anche la f.e.m.
(9)
Fig. 2. - Circuito equivalente dell'alternatore per lo studio
dell' autoeccitazione.
circuito
indotto
sull'asse d i r e t t o
derivante
dalla variazione del flusso φ.
Premesso q u a n t o sopra e con riferimento alla
figura 2 si possono scrivere le seguenti relazioni,
derivate d a l l ' a p p l i c a z i o n e del II p r i n c i p i o di Kirchhoff r i s p e t t i v a m e n t e alle maglie r a p p r e s e n t a t e dai
circuiti i n d u t t o r e , smorzatore ed i n d o t t o :
circuito
smorzatore
circuito
induttore
(4)
(1) La dizione « valore efficace istantaneo » è giustificata
dalla supposizione che la durata del fenomeno transitorio
in studio sia rilevante in confronto al periodo (ipotesi d) ).
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
275
e t e n e n d o conto della (10), la (9) diviene:
(12)
Date le ipotesi stabilite, detta equazione differenziale risulta, entro l'intervallo di t e m p o considerato « non omogenea ed a coefficienti costanti » e
la sua soluzione, t e n e n d o conto delle condizioni ai
limiti, v a l e :
(13)
essendosi indicato con t i l'istante iniziale dell'intervallo di t e m p o considerato, e con ε la base dei
logaritmi n a t u r a l i .
L'equazione algebrica (13) si c o m p o n e del termine
da
ritenersi
costante nell'intervallo di
t e m p o considerato, e del t e r m i n e
P r a t i c a m e n t e , stabilito il valore della capacità
C suscettibile di provocare l'autoeccitazione, la
q u a n t i t à B, data dalla seconda delle (11), in virtù
della variabilità del coefficiente ρ, decrescente al
crescere di e 2 , r i s u l t a :
B < 0 , nel p r i m o t r a t t o della caratteristica di eccitazione: in t a l caso l'esponenziale che
c o m p a r e nella (13) ha esponente positivo,
ciò che corrisponde ad un fenomeno esaltantesi nel t e m p o ;
B = 0, nel p u n t o della caratteristica di eccitazione la cui t a n g e n t e geometrica è parallela
alla caratteristica di carico capacitivo tracciata in figura 1; n e l l ' i n t o r n o di detto
p u n t o si vedrà che il fenomeno segue u n a
legge lineare col t e m p o ;
B > 0, nel r i m a n e n t e t r a t t o della caratteristica di
eccitazione: in q u e s t ' u l t i m o caso l'esponenziale ha esponente negativo ed in conseguenza il fenomeno va smorzandosi col
tempo.
Fig. 7. - Alcuni oscillogrammi forniti dalle prove per il
rilievo del parametro “ a „.
gura 4, risulterà formato da d u e rami : l ' u n o , p e r
i valori più bassi di e 2 , concavo verso l'alto, l'altro
invece concavo verso il basso; i d u e r a m i si raccordano fra di loro con un tratto p r a t i c a m e n t e rettilineo n e l l ' i n t o r n o del valore B = 0.
Nel caso che interessi conoscere l ' a n d a m e n t o
della corrente i 1 nell'avvolgimento di eccitazione,
la legge con cui essa varia in funzione del t e m p o
può essere facilmente ricavata dalle espressioni
sopra r i p o r t a t e . Infatti la p r i m a delle (6), t e n u t o
che la (13) fornisce:
presente che è
Fig. 3. - Procedimento per il rilievo dei parametri ρ ed e'2
dalla caratteristica di eccitazione.
n o n è esprimibile a n a l i t i c a m e n t e , si p u ò ovviare
o p e r a n d o entro intervalli di t e m p o sufficientemente
piccoli e conseguentemente con piccoli incrementi
di f.e.m. e 2 , tali che il t r a t t o di caratteristica interessato possa confondersi con la p r o p r i a t a n g e n t e .
I n d i c a n d o allora (figura 3) con e 20 il valore assunto dalla f.e.m. all'inizio dell'intervallo di t e m p o
considerato, con ρ il coefficiente angolare della tangente geometrica alla caratteristica di eccitazione
n e l p u n t o e 2 = e 2 0 , e con e' 2 l'intersezione di tale
t a n g e n t e con l'asse delle o r d i n a t e , la (8) si trasform a , entro tale intervallo di tempo, nella
diviene :
(14)
3.
(10)
e 2 = e'2 + ρi
e la (9) viene modificata in conseguenza.
Ponendo :
Fig. 6. - Schema per il rilievo del parametro “ a „.
Nel p u n t o di separazione B = 0, p e r il q u a l e la
(13) è i n d e t e r m i n a t a , ricercando il limite a cui essa
t e n d e p e r B t e n d e n t e a zero, si h a :
(11)
-
Determinazione
dei
parametri.
I p a r a m e t r i che, entro un d e t e r m i n a t o intervallo
di t e m p o , regolano il funzionamento della macchina sincrona autoeccitantesi sono essenzialmente
ρ ed A.
R i c o r d a n d o la definizione di ρ, dalla caratteristica di eccitazione si p u ò ricavare m e d i a n t e derivazione grafica tale q u a n t i t à in funzione della
f.e.m. e 2 ; dalla medesima caratteristica è opport u n o ricavare a n c h e la q u a n t i t à e' 2 in funzione
della stessa e 2 e r i u n i r e i d u e d i a g r a m m i in un
unico grafico. In figura 5 sono r i p o r t a t i tali diag r a m m i relativi alla macchina, su cui è stato speFig. 8. - Diagramma sperimentale della funzione
per la macchina su cui è stato sperimentato.
Fig. 4. - Andamento generico della funzione e 2 = f 1 (t).
Fig. 5. - Valori di ρ e di e'2 in funzione della f.e.m. stellata
per l'alternatore su cui è stato sperimentato.
che r a p p r e s e n t a nello stesso intervallo u n a tensione
variabile con legge esponenziale, la cui costante di
tempo
è variabile da istante a istante.
La quantità B ha u n a i m p o r t a n z a decisiva sia
nello stabilire il segno della tensione
che inter-
viene in a m b e d u e i t e r m i n i della (13), sia nel det e r m i n a r e il segno dell'esponenziale.
276
espressione che mostra la variazione lineare col
t e m p o annunziata in precedenza.
Premesso q u a n t o sopra, p e r ricavare la funzione e 2 = e 2 (t), basterà fissare un intervallo di
t e m p o (t-t i ) sufficientemente piccolo e ricercare il
valore che assume la e 2 alla fine di tale intervallo
m e d i a n t e l'espressione (13) impiegando in essa i
valori di ρ, B e E* spettanti al valore di e 2 raggiunto alla fine dell'intervallo p r e c e d e n t e e che
coincide adesso con e 2 0 ; e ciò iniziando dalla f.e.m.
dovuta al magnetismo residuo.
Il diagramma della funzione e 2 = e 2 (t) così otten u t o , il cui a n d a m e n t o generico è r i p o r t a t o in fiATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
277
Il coefficiente a della (15) v a l e :
dalle q u a l i è possibile ricavare sia la q u a n t i t à
utile p e r d e t e r m i n a r e l'effetto dello smorzamento
statorico (e con questo resta d e t e r m i n a t a A dalla
ed è d e t e r m i n a b i l e s p e r i m e n t a l m e n t e , rilevando
con oscillogramma la tensione ai morsetti della
macchina sincrona funzionante a vuoto ed eccitata
bruscamente con u n a c o r r e n t e di eccitazione che
interessi il t r a t t o iniziale rettilineo della caratteristica, p e r il quale ρ è p r a t i c a m e n t e costante.
Scegliendo da tale oscillogramma due o p p o r t u n i
valori di e 2 , e 2t' ed e 2 t " , corrispondenti agli istanti
t' e t", si p u ò ricavare a m e d i a n t e la seguente relazione dedotta dalla (15):
P e r q u a n t o verrà detto fra poco è necessario
eseguire varie prove con valori di R 1 diversi e
c o m p e n d i a r e i risultati in un unico d i a g r a m m a
P e r la m a c c h i n a in esame sono state ese-
Fig. 9. - Schema per le prove sperimentali sotto carico.
guite le prove descritte, i m p i e g a n d o lo schema di
figura 6. In figura 7 sono r i p o r t a t i esempi degli
oscillogrammi o t t e n u t i , m e n t r e in figura 8 è riport a t o il d i a g r a m m a
rimeritato. Noto ρ e fissato C, risulta subito determ i n a t a p e r ogni valore della f.e.m. e 2 a n c h e la
q u a n t i t à B t e n e n d o presente che il coefficiente K 2
e la reattanza di dispersione ωL d possono essere
d e t e r m i n a t i p r e l i m i n a r m e n t e con la nota prova a
carico t o t a l m e n t e reattivo.
La d e t e r m i n a z i o n e della q u a n t i t à A è invece
p i ù laboriosa. A m e n o che n o n si conoscano esatt a m e n t e p e r la m a c c h i n a in esame le grandezze di
cui A è funzione secondo la p r i m a delle (11) (ciò
che è assai raro), p e r d e t e r m i n a r e A occorre p r o cedere in m a n i e r a c o m b i n a t a sperimentale e analitica. Si osservi a tale scopo che qualora si esegua
la ricerca della e 2 = e 2 (t) p e r la macchina funzion a n t e a v u o t o , cioè con circuito esterno a p e r t o , si
perviene alla seguente espressione p e r tale funzione :
(15)
da essi ricavato.
Noto a si risale al p a r a m e t r o A, t e n u t o presente
che, dal confronto della p r i m a delle (11) con la
(16), si d e d u c e :
(17)
Questo ci dice che nella prova sotto carico, come è
n a t u r a l e , interviene nello stabilire il valore della
costante di t e m p o anche l'effetto dello smorzam e n t o statorico
nella cui espressione è
incognito u n i c a m e n t e il fattore
(17) ), sia la quantità
che r a p p r e s e n t a l'inver-
so della resistenza del circuito smorzatore r i p o r t a t a
al circuito i n d u t t o r e .
4.
-
Rilievi
sperimentali.
La m a c c h i n a sincrona a n i s o t r o p a , su cui è stato
sperimentato ( 2 ), ha le seguenti caratteristiche:
Potenza
Tensione n o m i n a l e
Corrente n o m i n a l e
N u m e r o dei poli
Frequenza
Collegamento
4 kVA
220 V
11,5 A
4
50 Hz
Fig. 11. - Confronto fra i risultati sperimentali e i risultati
teorici per le V2 ed i1 in funzione del tempo.
La sua caratteristica di eccitazione è r i p o r t a t a in
figura 1; dalla prova con carico c o m p l e t a m e n t e
reattivo sono stati dedotti il valore della sua reattanza di dispersione alla frequenza di 50 Hz
(ωL d = 1,125 Ω) ed il valore del coefficiente di reazione ( K 2 = 0,0666).
Lo schema dell'istallazione di prova è riport a t o in figura 9; il g r a p p o è dotato di un regolat o r e di velocità t i p o Dornig, che agisce sull'ecci-.
tazione del m o t o r e a c o r r e n t e continua di t r a i n o ,
m a , come è o p p o r t u n o rilevare, con u n a p r o p r i a
costante di t e m p o .
Su tale g r u p p o è stata condotta u n a serie di
prove con E 1 = 0, e capacità superiori al valore
limite di autoeccitazione.
La serie di prove compiute è consistita nella
(2) Tale macchina, insieme col motore a corrente continua e coi relativi accessori, è stata acquistata con i fondi
forniti dalla Associazione Nazionale Imprese Distributrici
di Energia Elettrica (ANIDEL) che gli Autori ringraziano.
esecuzione di t r e oscillogrammi (fig. 10); la macchina è stata ogni volta collegata ad u n a stessa t e r n a
di capacità (188,4 μ F, con collegamento a t r i a n golo) ma con valori diversi della resistenza R 1 del
circuito di r o t o r e .
Si è proceduto inoltre al calcolo della v 2 = e 2 (t),
seguendo i concetti illustrati n e l paragrafo 2, p e r
il valore di C stabilito e p e r gli stessi valori di R 1 :
sono stati così dedotti m e d i a n t e il calcolo t r e diag r a m m i che, messi a raffronto con gli analoghi
d i a g r a m m i sperimentali (fig. 11), p r o v a n o l'attendibilità del m e t o d o . Le discrepanze sono da attrib u i r e fra l ' a l t r o a l l ' e n t i t à delle tensioni e cori-enti
raggiunte, di p a r e c c h i e volte superiori ai valori nom i n a l i ; esse h a n n o fatto sì che le p e r d i t e n e l l ' a l t e r n a t o r e fossero u n a frazione considerevole della
potenza di t a r g a , e che, conseguentemente, p e r
l'improvviso carico, il m o t o r e rallentasse riprend e n d o p o i con relativa lentezza la velocità n o r m a l e .
Avendo a dispo-
sizione il diagramma di figura 8, stabiliti due diversi valori R 1 ' ed R 1 '' della resistenza rotorica, la
(16) ci fornisce due distinte relazioni:
Fig. 12. - Tratti dell'oscillogramma relativo alla prova con capacità limite.
(18)
come i m m e d i a t a m e n t e si deduce dalla (13), notando che a vuoto si ha C = C' = 0 e q u i n d i B = l.
Fig. 10. - Oscillogrammi forniti dalle prove sotto carico.
278
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
279
limite p e r l'innescarsi del fenomeno, e coincideva
con quella prevista con il calcolo.
La descrizione delle operazioni grafiche ed a n a litiche eseguite esorbita dai limiti imposti alla presente esposizione.
5.
Fig. 13. - Diagramma fornito dalla prova con capacità limite.
Nella stessa figura 11 sono r i p o r t a t i a n c h e i
d i a g r a m m i calcolati e rilevati della corrente nell'avvolgimento rotorico i 1 in funzione del t e m p o .
L'oscillogramma di figura 12 si riferisce invece
ad u n a prova eseguita con capacità p a r i al valore
limite calcolato (141 µF con collegamento a triangolo); di tale oscillogramma p e r ragioni p r a t i c h e
sono stati r i p o r t a t i solamente tre t r a t t i ma i dati
da esso forniti sono stati riassunti nel diagramma di
figura 13. È interessante n o t a r e come nei primi
istanti si sia avuto un inizio di autoeccitazione che
è successivamente cessato, p r o b a b i l m e n t e per la
diminuita velocità della macchina, stabilizzandosi
la tensione ai morsetti ad un valore di poco superiore alla f.e.m. dovuta al magnetismo residuo.
In seguito p e r qualche causa accidentale è aum e n t a t a , sia p u r e di poco, la velocità del g r u p p o
e il fenomeno ha avuto inizio di nuovo, svolgendosi secondo l ' a n d a m e n t o previsto.
L'instabilità riscontrata dimostra che la capacità con cui si è operato era effettivamente quella
- Conclusione.
Lo studio compiuto ha permesso di individuare
i p a r a m e t r i che d e t e r m i n a n o l ' a n d a m e n t o nel tempo del fenomeno di autoeccitazione. Essi possono
essere calcolati in sede di progetto o p p u r e essere
rilevati in sede di collaudo m e d i a n t e prove assai
semplici, che non richiedono di sottoporre la macchina a carico nè attivo nè reattivo. Conoscendo il
valore di tali p a r a m e t r i è possibile stabilire con
sufficiente esattezza, almeno p e r q u a n t o riguarda
il fenomeno dell'autoeccitazione, la m i n i m a velocità con cui devono intervenire i regolatori di tensione.
Mario Picchi, Alfredo Vallini
Pisa
-
Istituto
di
Elettrotecnica
dell'Università.
BIBLIOGRAFIA
C. PALESTRINO e C. CAMINITI, Tecnica degli Impianti Elettrici, UTET, Torino, 1934.
P. WALDVOGEL, Theorie der Spannungshaltung einer auf eine
lange leerlaufende Leitung arbeitenden Drehstrommaschine, Brown Boveri Miti., 1945, XXXII, pag. 251.
R. KELLER, Die Beherrschung der Selbsterregung bei
Synchrongeneratoren, Bullettin de l'Ass. Suisse des
Electr., 1949, XL, pag. 173.
C. LAVANCHY, La stabilité des génératrices synchrones, Revue Brown Boveri, 1949, XXXVI, pag. 264.
]. HERLITZ, Problèmes relatifs au fonctionnement des réseaux de transport d'energie a haute tension et a grande
distance, C.I.G.R.E., Parigi 1949, Tomo III, Rapporto
n. 406.
a Giancarlo Vallauri
Stato attuale degli studi sulla trasmissione d'energia
a corrente continua ad alta tensione
Riassunti gli studi compiuti o in corso di esecuzione sulla trasmissione d'energia a corrente continua ad
alta tensione, si accenna a quelli che verranno effettuati presso l'I.E.N.G.F. e si considera la convenienza
che esperienze di esercizio vengano compiute in Italia.
1.
- Indirizzo generale degli studi.
Le esperienze sulla trasmissione a corrente continua ad alta tensione con sottostazioni di conversione a vapore di mercurio ebbero inizio poco prima dell'ultima guerra. A b b a n d o n a t o il vecchio
concetto di T h u r y della produzione diretta dell'energia a corrente continua ad alta tensione, si
delineò con esse la figura dell'impianto m o d e r n o di
trasmissione a corrente continua, con produzione
mediante generatori trifasi e doppia conversione,
da corrente alternata in corrente continua in partenza, da corrente continua in corrente alternata all'arrivo. L'uso dei convertitori a vapore di mercurio p e r la doppia conversione fu conseguenza del
progresso costruttivo dei commutatori corrispondenti, che, soprattutto con l'introduzione delle griglie di comando e di elettrodi ausiliari fra anodo
280
e catodo, consentivano nella maniera migliore la
conversione nei due sensi a tensione elevata: altri
c o m m u t a t o r i , quelli di Marx, ad arco in aria compressa, p u r e studiati p e r le alte tensioni, non riuscivano altrettanto convenienti, così che furono scartati all'atto degli studi, di poco posteriori, p e r la
progettazione e l'esecuzione della linea Elba-Berlino, di cui sarà fatta parola in seguito.
In questo tipo di i m p i a n t i , il sistema di produzione e quello di trasmissione p e r m e t t o n o di u n i r e
i vantaggi economici della produzione mediante generatori trifasi e quelli della trasmissione a corrente continua attraverso linee, aeree o in cavo, a
due o addirittura a un solo conduttore, con ritorno
p e r il t e r r e n o . P e r contro la doppia conversione
accresce il costo complessivo degli i m p i a n t i , atten u a n d o e a n n u l l a n d o a volte, secondo i valori delle
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
potenze da trasmettere e delle distanze di trasmissione, e il percorso della linea, i vantaggi economici del sistema di trasmissione.
Mentre nei confronti della trasmissione a corrente continua con produzione diretta di energia di
questa forma, la trasmissione a corrente continua
con produzione a corrente trifase e doppia conversione ha ottenuto u n a facile prevalenza, nei confronti con la trasmissione trifase si è stabilita u n a
competizione, che, risoltasi nel periodo immediatamente successivo alla guerra a favore della trasmissione trifase a tensione oltre 200 kV e fino a 400 k V ,
non p u ò dirsi ancora chiusa.
2.
- Schemi usati. Esperienze passate o in corso di
esecuzione.
Due schemi di trasmissione a corrente raddrizzata furono sperimentati da principio, quello in
serie, a corrente costante, seguendo in questo il concetto classico di T h u r y , quello in derivazione, a
tensione costante, più corrispondente, come modalità d'esercizio, agli usuali impianti di trasmissione
tritasi.
Negli Stati Uniti d'America, fra Schenectady e
Mechanicville, nel 1936, la G.E.C. eseguì la trasmissione sperimentale di circa 180 A a 15 k V , col
sistema a corrente costante, servendosi dello schema
monociclico di Steinmetz p e r passare dal circuito a
tensione costante del generatore a quello a corrente
costante del trasformatore, del commutatore e della
linea di trasmissione, o viceversa da questo a quello
dell'utilizzatore (fig. 1) [ 1 ] . Tale schema non ha
avuto diffusione in seguito, forse anche in conseguenza del fatto che al problema della trasmissione
a corrente continua non sono state dedicate in America ulteriori speciali attenzioni, essendosi rivolte
piuttosto le case costruttrici a m e r i c a n e , specie
dopo la guerra, verso lo studio dei problemi della
trasmissione trifase a tensione superiore a 220 k V .
Tutti gli studi compiuti e in corso di esecuzione
in E u r o p a sono stati effettuati invece su linee di
trasmissione a tensione costante. Lo schema dei
convertitori prescelto il più delle volte è quello
trifase di Graetz, che meglio si adatta alle alte tensioni d'esercizio, perchè comporta il m i n o r valore
della tensione inversa, eguale a quello della tensione raddrizzata, anzichè circa d o p p i o di essa, come avviene negli schemi con conduzione a u n a sola
via. P e r le tensioni di esercizio maggiori sono stati
usati o previsti più gruppi tritasi connessi in serie in
ogni convertitore ed eventualmente più elementi
di commutatori in serie nello stesso lato dello schema. Usando elementi dei tipi più recenti, che possono sostenere con piena sicurezza u n a tensione di
esercizio di 50 k V , lo schema della fig. 2, con due
gruppi in serie fra loro e due elementi di commutatore in serie in ogni lato dello schema, p e r m e t t e
di effettuare una trasmissione a 200 k V : m e t t e n d o
a terra il p u n t o di connessione fra i due g r u p p i , i
due conduttori di linea si trovano a potenziali di
100 k V ; con una corrente continua di 250 A, che
p u ò facilmente ottenersi con gli elementi indicati,
è possibile trasmettere una potenza di 50 M W .
Fig. 1. - Trasmissione a corrente costante con schema monociclico di Steinmetz.
L'uso di elementi per tensioni più elevate o p e r
correnti più intense, che non è impossibile costruire, consentirebbe la trasmissione di potenze
proporzionalmente maggiori. Con elementi simili e
schemi più semplici costituiti da un solo g r u p p o
avente un elemento in ogni lato del commutatore
( q u i n d i c o m p r e n d e n t e 6 elementi di commutatore
in tutto) è possibile effettuare la trasmissione di potenze dell'ordine di 12-15 M W , a 50-60 k V , con
un estremo di un convertitore a terra o con ritorno
p e r la terra.
Il p r i m o i m p i a n t o a tensione costante ad alta
tensione, sperimentato in E u r o p a , fu installato
dalla B.B.C. di Baden nel 1939, fra Wettingen e
Zurigo (30 km), in occasione dell'Esposizione nazionale svizzera tenuta q u e l l ' a n n o in quella città
[ 2 ] . La potenza trasmessa era di 500 k W , la tensione di 50 k V . Lo schema dei convertitori era con
conduzione a u n a sola via (fig. 3); i c o m m u t a t o r i ,
polianodici, erano in cilindro di acciaio.
A p a r t e le esperienze, di poco successive, sull ' i m p i a n t o da L e h r t e a Misburg (Hannover-Braunschweig) p e r la trasmissione di 16 MW a 80
kV con convertitori equipaggiati con c o m m u t a t o r i
di Marx ad arco in aria compressa, che avevano p e r
scopo la messa al p u n t o di questi commutatori e
n o n h a n n o avuto seguito, come già è stato accenn a t o , numerose esperienze sono state eseguite in
E u r o p a a p a r t i r e da quegli a n n i , con convertitori
a vapore di mercurio, quasi sempre in cilindro di
acciaio [ 3 ] .
La Siemens aveva eseguito delle prove a Siemensstadt, fin dal 1937, con ampolle monoanodiche in vetro, a 75 k V , 4 A raddrizzati, e altre ne
compì anni d o p o , fra Charlottenburg e Moabit (di-
ATTI E RASSEGNA TECNICA DELLA SOCIETÀ DEGLI INGEGNERI E DEGLI ARCHITETTI IN TORINO - ANNO 6 - N. 8-9 - AGOSTO-SETTEMBRE 1952
281












