BREVI NOTE SUL PROBLEMA DEL CENTRO DI TAGLIO

BREVI NOTE SUL PROBLEMA DEL CENTRO DI TAGLIO
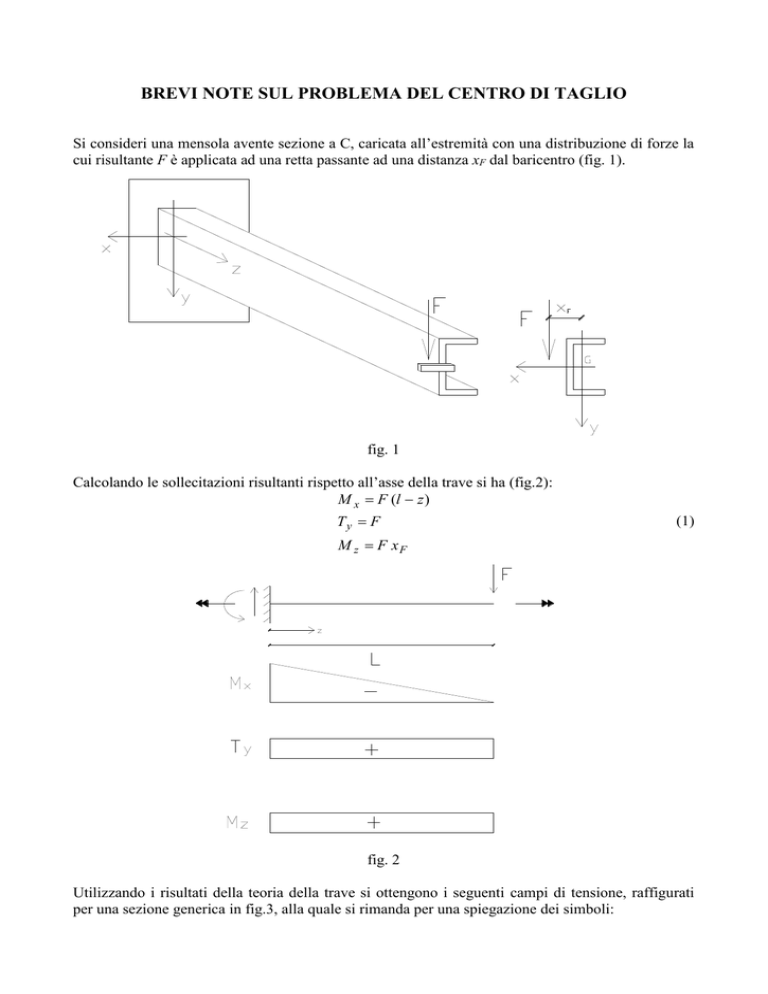
Si consideri una mensola avente sezione a C, caricata all’estremità con una distribuzione di forze la
cui risultante F è applicata ad una retta passante ad una distanza xF dal baricentro (fig. 1).
fig. 1
Calcolando le sollecitazioni risultanti rispetto all’asse della trave si ha (fig.2):
M x  F (l  z )
Ty  F
(1)
M z  F xF
fig. 2
Utilizzando i risultati della teoria della trave si ottengono i seguenti campi di tensione, raffigurati
per una sezione generica in fig.3, alla quale si rimanda per una spiegazione dei simboli:
z 
Mx
F (l  z )
y
y
Ix
Ix
 zx 
T y s1 (h  d 1 ) 2 M z d 1

Ix
2
Jt 2
 zy 
T y  s1 d 1 (h  d 1 ) s 2 (h  s 2 )  2 M z d 2

 

I x 
2 d2
2
Jt 2


sulle ali
sull' anima
(2)

1
2 a d 13  (h  d 1 )d 23
3
2
3
 a d 13
a h 2 d1 h 3 d 2
 h  d 1   d 2 (h  d 1 )
I x  2
 a d1 


 
12
2
12
 2  
 12
Jt 
fig. 3
Si valutino ora le risultanti ed i momenti risultanti delle tensioni indicate in (2). In particolare con
R1=R3, R2 si indicano le risultanti delle tensioni tangenziali sulle ali e sull’anima del profilato, che
si ottengono semplicemente valutando l’area sottesa al diagramma delle tensioni tangenziali da
taglio, e moltiplicando il risultato per lo spessore dell’elemento considerato, fig. 4. Dal momento
che la tensione tangenziale da taglio all’estremità dell’ala e sull’asse baricentrico (tensione
tangenziale massima da taglio) sono date rispettivamente da
F a ( h  d1 ) F a h
 zA 

Ix
2
Ix 2
(3)
2
2
F 1  a d1 ( h  d 1 ) d 2  h
  F  a h d1 h 
 z max 



  d1   
I x d 2 
2
2 2
8 
  I x  2 d 2
le risultanti delle tensioni tangenziali sulle ali e sull’anima del profilato sono (si noti che la
risultante delle tensioni tangenziali da torsione è ovviamente nulla):

fig. 4
R1   zA
a d1 F a ( h  d1 ) a d1 F a 2 h d1


2
Ix
2
2
Ix
4
d1
d 
2
(h  2 d1 ) d 2    z max   zA 1 (h  2 d1 ) d 2 
d2
3
d2 
(4)
2
d1 a ( h  d1 ) 
F a ( h  d1 )
2 F  d1 a ( h  d1 ) 1  h


( h  2d1 ) d1 
   d1  

 ( h  2d1 ) d 2 
Ix
2
3 I x  d 2
2
22
d2
2


R2   zA
 a h 2 d1 h 3 d 2 

F

 2

12


Utilizzando i risultati (4) si ottengono infine il risultante ed il momento risultante delle tensioni
agenti sulla sezione (si noti che nel momento torcente risultante compare anche il contributo delle
tensioni tangenziali da torsione):
M x   F (l  z )
F

Ix
Ty  F
F a 2 h 2 d1
M z  R1 (h  d1 )  R2 x1  F x F 
 Fx1  F x F ˆ F ( xC  x F )
Ix
4
(5)




2 2
2
a 2 h 2 d1
a
h
d
a
d
1
1
1
 1  1 
xC 
 x1 


a
 2   

4Ix
4 ah 2 d1 h 3 d 2 2ad1  hd 2
2


3


2
12
d
h

 1
a
d2
Pertanto la distribuzione ipotizzata per le tensioni tangenziali produce un momento torcente
risultante diverso da quello generato dalla forza F, che deve essere corretto mediante una
distribuzione di tensioni tangenziali prodotte da un momento torcente –F xC. Il momento torcente
totale agente sulla sezioni sarà allora pari a
M z  F  x F  xC 
(6)
Solo se la forza F è applicata ad una distanza xF=xC dal baricentro della sezione, il momento
torcente agente su questa risulta nullo.
Il punto per il quale passa la risultante delle tensioni tangenziali da puro taglio, o, in altri termini, il
punto al quale si deve applicare la forza di taglio perché il momento torcente risulti nullo, viene
detto Centro di Taglio. In tutti gli altri casi sulla sezione agisce un momento torcente pari al
momento della forza di taglio rispetto al centro di taglio (formula 6).
Nel caso in esame il cento di taglio si trova spostato alla sinistra del baricentro della sezione di una
quantità pari a xC. Da un punto di vista operativo la posizione del centro di taglio si può facilmente
determinare calcolando le tensioni tangenziali da puro taglio e valutandone poi l’asse centrale, per
esempio calcolando il momento risultante di questa distribuzione rispetto ad un punto fissato. Il
rapporto tra questo momento risultante ed il valore del taglio fornisce la distanza del centro di taglio
dal punto fissato. La posizione del centro di taglio dipende solo dalle caratteristiche geometriche
della sezione.
Nel caso della sezione a C la posizione del centro di taglio, oltre che nel modo illustrato sopra, si
poteva anche valutare calcolando il momento risultante delle tensioni tangenziali da taglio rispetto
ad un punto O dell’anima del profilato (fig. 5). Risulta in questo caso
(7)
M O  R1h
La posizione del centro di taglio rispetto al punto O risulta pertanto
M O a 2 h d1
(8)
xO 

 xC  x1
F
4Ix
cioè si ottiene lo stesso punto calcolato precedentemente.
fig. 5
La trattazione è stata condotta nell’ipotesi semplificata che la flessione agente sulla sezione sia
retta. Nel caso generale in cui sulla sezione agisce una forza di modulo F e direzione data dal
versore d, e detto F un punto qualunque della retta d’azione della forza, la relazione (6) diventa
(fig.6)
M z  F rF  rC   d  e z 
fig. 6
E’ istruttivo osservare lo stesso problema da un punto di vista cinematico. A tal fine si definisce
rotazione della sezione di estremità della mensola di fig. 1 quella determinata mediante il principio
dei lavori virtuali utilizzando come sistema degli spostamenti quello di figura 1, sul quale agisce la
forza F lungo una direzione di versore d, e come sistema virtuale delle forze la mensola di fig. 7
caricata all’estremità da una coppia torcente unitaria, cioè
fig. 7
l
1 z  F  
0A
M
z
 Tz
dA dz
G
(9)
in cui con l’apice M si indicano le tensioni tangenziali generata da un carico avente risultante nulla
e momento risultante M z  1 , mentre con l’apice T si indicano le tensioni tangenziali generate da
un carico avente risultante T  1 . Si definisca Centro di Taglio il punto dove deve essere applicata
tale risultante affinché risulti nulla la rotazione (9) della sezione, cioè perché sia
M T
(10)
  z  z dA  0
A
Applicando il teorema di Betti la condizione (10) implica le seguenti uguaglianze:
1
T
M
M z  1, T  1
z  z dA  M z  z  T  s c  0

GA
(11)
La prima conferma che la rotazione torsionale della trave caricata con una forza passante per il
centro di taglio è nulla, mentre la seconda afferma che nella trave caricata con una coppia torcente è
nullo lo spostamento del centro di taglio, cioè che la rotazione torsionale della sezione avviene
attorno al centro di taglio.
Pertanto se il taglio è applicato al centro di taglio la sezione non subisce rotazione torsionale. In
base a quanto dimostrato, se sulla sezione agisce un taglio nella direzione individuata dal versore d,
non passante per C la trave subirà sia uno spostamento sia una rotazione intorno all’asse z. Le
tensioni tangenziali agenti sulla trave saranno date da
(12)
 z  F Tz  rF  rC   d  e z  M
z
cioè esse si possono valutare come somma delle tensioni tangenziali dovute al taglio puro applicato
al centro di taglio più quelle causate da un momento torcente necessario per trasportare la forza F
nel centro di taglio. Lo spostamento di un punto P della sezione nella direzione dP si può calcolare
valutando il lavoro virtuale compiuto dalle tensioni tangenziali in equilibrio con una forza unitaria
applicata in P per le deformazioni dovute alla forza reale,

l


1  v P    1   Tz  (rP  rC )  d P  e z  M
z
0A
l

 
F
 T
 z


G 0 A
2
 G1 F 
 d
M
  Tz  M
z d P  d F    z
d P  (rP  rC )  d P  e z 
Utilizzando la (10) si ha
2
T
z

 (rF  rC )  d F  e z  M
z dA dz 
PdF
 dA dz


(13)
d F  (rF  rC )  d F  e z 
l
     d
F
1  v P     Tz
G 0 A
2
M 2
z
P
d F  dA dz

(14)
Il primo integrale fornisce il contributo della deformabilità a taglio allo spostamento dell’estremità
della mensola, essendo uguale allo spostamento del centro di taglio causato da una forza di modulo
F applicata ad esso, e si pone (kx, ky sono i fattore di taglio nel caso gli assi x,y siano principali di
flessione)
l
Fy l
Fx l
F
T 2
(15)

dA
dz


ˆ
z
G 0 A
k x GA k y GA
 
Il secondo termine dell’integrale è lo spostamento del punto P dovuto ad una rotazione torsionale
della sezione attorno al centro di taglio causato dal momento torcente F dF, cioè il momento
necessario per trasportare la forza F nel centro di taglio.
In definitiva si hanno due metodi per determinare la posizione del centro di taglio. Uno è quello di
determinare la posizione del punto C annullando l’integrale (10). Tale metodo è utile quando si
conoscano i campi della tensione tangenziale provocati sia da un momento torcente sia da una forza
unitaria applicata ad una retta generica della sezione. L’altro metodo è valutare la posizione del
centro di taglio con una espressione simile alla (6), calcolando le tensioni tangenziali da taglio puro
e poi valutandone il momento torcente risultante rispetto ad un prefissato punto della sezione. Tale
metodo è particolarmente utile quando si utilizzano espressioni approssimate per il campo di
tensioni tangenziali da taglio, come quelle date dalla trattazione di Jourawski per le sezioni sottili.
Utilizzando questo secondo metodo è immediato determinare la posizione del centro di taglio per
profilati a sezione sottile, quando al sezione è formata da due lati. Infatti in tal caso il centro di
taglio si trova all’intersezione della linea media dei due lati. Infatti, qualunque sia la distribuzione
delle tensioni tangenziali da taglio, la risultante parziale per ciascun lato è sempre applicata alla
linea media del rispettivo lato, e la risultante globale deve necessariamente essere applicata ad una
retta passante per il punto di intersezione delle due linee medie (fig. 8).
fig. 8
Per una sezione a C, in alternativa a quanto fatto nella (5,6) si può più convenientemente valutare il
momento risultante delle tensioni tangenziali da taglio puro rispetto al punto O di intersezione
dell’asse x con la linea media del lato verticale della sezione. Il rapporto fra il momento e l’intensità
del taglio fornisce la distanza del centro di taglio da tale punto (fig.5):
Rh
xC  x O  1
F