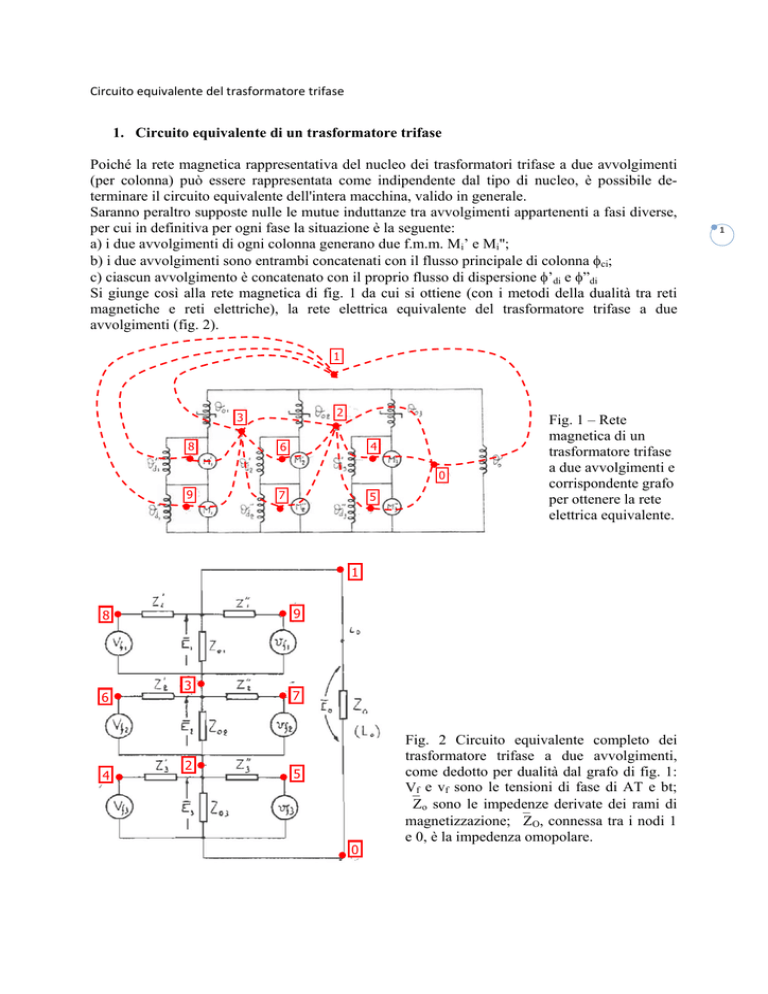
Circuito equivalente del trasformatore trifase 1. Circuito equivalente di un trasformatore trifase
Poiché la rete magnetica rappresentativa del nucleo dei trasformatori trifase a due avvolgimenti
(per colonna) può essere rappresentata come indipendente dal tipo di nucleo, è possibile determinare il circuito equivalente dell'intera macchina, valido in generale.
Saranno peraltro supposte nulle le mutue induttanze tra avvolgimenti appartenenti a fasi diverse,
per cui in definitiva per ogni fase la situazione è la seguente:
a) i due avvolgimenti di ogni colonna generano due f.m.m. Mi’ e Mi";
b) i due avvolgimenti sono entrambi concatenati con il flusso principale di colonna ci;
c) ciascun avvolgimento è concatenato con il proprio flusso di dispersione ’di e ”di
Si giunge così alla rete magnetica di fig. 1 da cui si ottiene (con i metodi della dualità tra reti
magnetiche e reti elettriche), la rete elettrica equivalente del trasformatore trifase a due
avvolgimenti (fig. 2).
1
2
3
8
4
6
0
9
7
5
Fig. 1 – Rete
magnetica di un
trasformatore trifase
a due avvolgimenti e
corrispondente grafo
per ottenere la rete
elettrica equivalente.
1
9
8
6
4
3
2
7
5
0
Fig. 2 Circuito equivalente completo dei
trasformatore trifase a due avvolgimenti,
come dedotto per dualità dal grafo di fig. 1:
Vf e vf sono le tensioni di fase di AT e bt;
Zo sono le impedenze derivate dei rami di
magnetizzazione; ZO, connessa tra i nodi 1
e 0, è la impedenza omopolare.
1
Circuito equivalente del trasformatore trifase La rete di fig.2 è corrispondente al circuito equivalente completo del trasformatore ed infatti per
ogni colonna avvolta compare un gruppo di impedenze a T; inoltre le tensioni ai morsetti di AT e
bt sono quelle di fase, e andranno collegate tra loro per ottenere un circuito trifase (con tre
morsetti per lato), tenendo anche conto dei numeri di spire degli avvolgimenti di AT e bt.
Per effettuare i collegamenti è necessario inserire 6 trasformatori ideali (3 sul lato AT e 3 sul lato
bt) con gli avvolgimenti cui fanno capo i morsetti esterni, collegati nel modo desiderato (Y o D).
E' immediato passare ora al circuito equivalente ridotto, in cui leZ’ eZ” sono conglobate in
un'unica impedenza serieZs, avendo portato a monte la impedenza derivataZo. L'intero circuito
assume la configurazione di fig. 3: la figura è relativa ad un trasformatore a collegamento stellatriangolo (Yd), ma anche gli altri tre casi possibili sono rappresentabili (Yy, Dy, Dd).
Fig. 3 – Circuito equivalente ridotto di un trasformatore trifase a due avvolgimenti (colleg.
stella/triangolo: Yd).
Il circuito equivalente del trasformatore trifase mostra che quando c1 +c2 +c3 = 0 (cui
consegue ancheE1 +E2 +E3 = 0), ossia manca il flusso omopolare, la macchina si comporta
esattamente come tre trasformatori monofasi indipendenti. Questa condizione (che per il fatto di
legare a somma nulla i flussi è denominata a “flussi vincolati”) si verifica in pratica quando vi è
simmetria nelle tensioni ed equilibrio nelle correnti.
La presenza del flusso omopolare (O = LO IO) corrisponde alla circolazione di una corrente
omopolareIO nelle tre impedenze di magnetizzazione, cui consegue una dissimmetria delle
f.e.m. indotte.
Come meglio chiarito nel paragrafo che segue, nel caso di trasformatori a tre colonne l'alto
valore assunto dalla riluttanza omopolare O determina un flusso O di valore modesto per una
data d.d.p. magnetica; in eguali condizioni in un trasformatore a cinque colonne (detto anche a
flussi liberi, perché c1 +c2 +c3 0) il flusso O è molto maggiore e più vistosa la
dissimmetria delle f.e.m..
2
Circuito equivalente del trasformatore trifase 2. Disposizioni e proprietà dei nuclei magnetici trifase
Il nucleo a 3 colonne dei trasformatori trifase ha la sua genesi nella struttura magnetica spaziale
con gioghi connessi a stella, come mostrato in fig. 4: in pratica tale struttura, di difficile
costruzione, lascia poi il passo alla disposizione planare di fig. 5, nella quale la colonna centrale
presenta una lunghezza media inferiore a quella delle colonne laterali.
3
Fig. 5 – Nucleo trifase a 3 colonne, ottenuto
per “schiacciamento sul piano” della struttura
Fig. 4 – Nucleo trifase a 3 colonne, con gioghi di fig. 1, con gioghi complanari.
connessi a stella
Poiché tra i nodi magnetici N e M il tubo di flusso esterno alle colonne è ad alta riluttanza perché
si svolge in aria (si tratta della riluttanza omopolare O di fig.1). Dunque, il flusso omopolare O:
O = a + b + c
è modesto: per questa ragione un trasformatore trifase con nucleo a 3 colonne è usualmente
denominato come “a flussi vincolati”, nel senso che a + b + c = O 0.
In fig. 6 è mostrata la mappa di campo magnetico di tipo omopolare (dovuta a 3 f.m.m. di
colonna uguali e in fase tra loro).
Fig. 6 – Nucleo a 3 colonne: campo magnetico del flusso omopolare, prodotta da 3 f.m.m. uguali
e in fase tra loro: le linee di campo si sviluppano in aria, nello spazio circostante al nucleo.
Circuito equivalente del trasformatore trifase E' naturalmente possibile concettualmente realizzare un circuito magnetico trifase i cui gioghi
siano collegati a triangolo ad entrambe le estremità, come mostrato in fig. 7. In questo caso tra i
flussi nelle colonne c e i flussi nei gioghi g esistono le note relazioni di ampiezza e di fase
relative ad un circuito elettrico a triangolo, in particolare:
g = c / 3 0.577c .
4
Fig. 7 – Circuito magnetico trifase con gioghi connessi a triangolo ad entrambe le estremità: in
tal caso i flussi di colonna e di giogo sono legati come mostrato nel diagramma fasoriale a lato.
Ovviamente i nuclei con gioghi connessi a triangolo sono di difficile costruzione. Se però si
sezionano due gioghi, come indicato in fig. 8 a, collegando quello superiore ed inferiore con una
colonna di sezione uguale a quella dei gioghi (fig.8 b), e si sviluppa in piano questa struttura (fig.
8 c), è evidente che il funzionamento di questa configurazione a 5 colonne non è mutato rispetto
a quello di fig. 7. Naturalmente, le due colonne laterali e i gioghi della struttura a 5 colonne
hanno sezione 1/3 volte quella delle colonne centrali avvolte, come meglio mostrato in fig. 9.
La rete di riluttanze che lo rappresenta è identica a quella di fig. 1 se si conglobano in una sola le
riluttanze delle due colonne laterali (che di fatto sono in parallelo tra loro). Unica differenza è
che mentre il flusso omopolare nel nucleo a tre colonne percorre un circuito magnetico in aria,
nel nucleo a cinque colonne questo si svolge nel ferro, come mostrato in fig. 10. Dunque in tal
caso la permeanza omopolare è assai più elevata rispetto a quella di un nucleo a 3 colonne;
quindi il flusso omopolare è consistente; quindi il nucleo viene denominato “a flussi liberi”,
perché risulta:a + b + c = O 0.
c
Fig. 8 – Genesi di un nucleo a 5 colonne a gioghi complanari, equivalente a quello di fig. 7.
Circuito equivalente del trasformatore trifase 5
Fig. 9 – Disegno schematico del nucleo a 5 colonne con gioghi complanari: le sezioni delle
colonne laterali e dei gioghi sono pari a 1/3 volte quella delle colonne centrali avvolte.
Fig. 10 – Nucleo a 5 colonne: campo magnetico del flusso omopolare, prodotta da 3 f.m.m.
uguali e in fase tra loro: il campo è confinato nel nucleo, richiudendosi nelle colonne laterali.
Non vi sono ragioni teoriche per cui i nuclei a tre ed a cinque colonne si differenzino, per cui
data la maggior semplicità, viene di regola impiegato il nucleo a tre colonne; solo nei casi in cui
la macchina risulti troppo alta, e ne sia difficoltoso il trasporto, si passa all'esecuzione a cinque
colonne che consente la limitazione dell’ingombro in altezza, come mostrato in fig. 11.
Infine, la permeanza omopolare è elevata anche nel caso in cui si adottino 3 nuclei monofase per
realizzare una unità trifase, perché anche in questo caso il circuito magnetico è “a flussi liberi”.
Fig. 11 – Confronto delle dimensioni di nucleo, a pari dimensioni di avvolgimenti, tra una
soluzione a 3 e a 5 colonne (Hf = altezza finestra; D = diametro colonna; I = interasse colonne).












