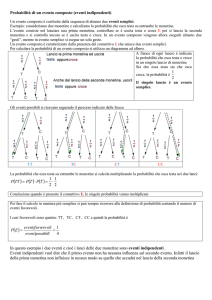
PERCORSO PROBABILITÀ
Scuola Primaria / Scuola Secondaria 1° grado
Dipartimento di Matematica
a.s. 2009/2010
Istituto Comprensivo “Padre Gemelli” - Torino
Docenti:
Carbone Giuseppina (I.C. Padre Gemelli – Scuola secondaria 1°grado)
Chiarelli Maria Teresa (I.C. Padre Gemelli – Scuola Primaria)
Costantino Annalisa ( I. C. Borgata Paradiso - Collegno -Scuola Primaria)
De Giorgi Maria Luisa (I.C. Padre Gemelli – Scuola Primaria)
Franceschetti Laura (I.C. Padre Gemelli – Scuola Secondaria 1°grado)
Gobbino Ezia (I.C. Padre Gemelli – Scuola Primaria)
Listi Monica (I.C. Padre Gemelli – Scuola Primaria)
Maragò Francesca (I.C. Padre Gemelli – Scuola Primaria)
Marani Maura (I.C. Padre Gemelli – Scuola Primaria)
Migliarese Melania (D.D. Anna Frank – TO – Scuola Primaria)
Rubatto Marilena (I.C. Padre Gemelli – Scuola Primaria)
Suddivisione argomenti per classi
Scuola Primaria
classe prima
classe seconda
classe terza
classe quarta e quinta
Argomenti
certo e impossibile
possibile
certo – possibile – impossibile
introduzione al concetto di probabilità
secondo la concezione classica
cos’è un evento –
casi favorevoli/ casi possibili1
Scuola Secondaria 1°grado
classe prima
classe seconda
classe terza
1
Altro modo di presentare la frazione.
Si rimanda a statistica.
3
Si rimanda a statistica.
2
grafici2
moda, media, mediana3
probabilità secondo la concezione classica
eventi dipendenti ed indipendenti
eventi compatibili ed incompatibili
introduzione al concetto di probabilità
frequentista
PROBABILITA’
CONCETTI/PAROLE CHIAVE: DEFINIZIONI POSSIBILI
EVENTO: qualunque cosa si possa analizzare, può succedere ed è oggettivo. Es.: lancio del
dado.
SFACCETTATURE DEGLI EVENTI:
POSSIBILE: la possibilità che esca un numero compreso tra 1 e 6 lanciando un dado.
CERTO: la certezza che esca un numero > 0 e ≤ 6 nel lancio di un dado.
IMPOSSIBILE: l’impossibilità che esca un numero > 6 nel lancio di un dado.
FAVOREVOLE: lanciando sei volte un dado si ha il 50% di evento favorevole che esca un numero pari.
FREQUENZA: il numero di eventi favorevoli sul totale eseguito.
PROBABILITÀ: ANALISI DELLE DIVERSE CONCEZIONI (DAL LIBRO:”PRIMO
INCONTRO CON LA PROBABILITA’” - Dupont)
Ci sono varie concezioni:
concezione classica;
concezione frequentista;
“
“
assiomatica;
concezione soggettivista.
La parola probabilità, come molte altre parole, ha nel linguaggio comune un significato
approssimativo; nel linguaggio scientifico il significato dovrebbe invece essere preciso.
1) CONCEZIONE CLASSICA
( a priori)
Lancio 1 dado: la probabilità che esca il 5 è 1 su 6 (1/6);
Lancio 2 dadi: le probabilità che esca 5 sono 1 su 9 (1/9)
Rappresentazione con tabella:
se lancio 2 dadi le possibilità che esca 5 sono 4 su 36 ovvero 1 su 9
1
1
2
3
4
5
6
2
3
4
*
5
6
*
*
*
* somma = a 5
Estraiamo 1 carta da un mazzo di 52:
la probabilità di estrarre un fante è 4 su 52;
la probabilità di estrarre 1 carta di cuore 1 su 4;
“
“ “
“
un fante di cuore 1 su 4;
La probabilità di estrarre una figura 3 su 13.
Questa concezione non è la migliore, ma è da preferire quando si introduce la probabilità.
2) CONCEZIONE FREQUENTISTA
( a posteriori)
Abbiamo un sacchetto che contiene 100 palline uguali (non sappiamo quante sono
quelle bianche)
? di palline bianche
Estraiamo una pallina: può essere bianca oppure no;
rimettiamo la pallina nel sacchetto;
estraiamo un’altra pallina e così via per 1000 volte.
Alla fine le palline bianche sono 703.
Possiamo dire che la frequenza è 703 su 1000.
(La frequenza relativa sarà all’incirca 7 su 10).
Se facciamo 50 estrazioni di 1 pallina per volta con reimbussolamento:
La frequenza è all’incirca 36/50 = 72/100 = 0,72
frequenza relativa
Facendo altre estrazioni si potrebbero avere altre frequenze.
Anche la concezione frequentista può essere usata sul piano didattico con buoni risultati.
3) CONCEZIONE SOGGETTIVISTICA
La probabilità è la misura del grado di fiducia che un soggetto coerente attribuisce
all’avverarsi di un evento:
Scommesse (calcio, cavalli ecc…..)
4) IMPOSTAZIONE ASSIOMATICA (astrae la probabilità, non c’è più riferimento
concreto e si lavora con insiemi e intersezione di insiemi….)
Queste due ultime si usano oltre la scuola media.
LA CONCEZIONE CLASSICA IN PROSPETTIVA DIDATTICA
Se lancio 1 dado:
- con quante probabilità viene un numero > di 4
E = evento
E = viene un numero > di 4
La probabilità dell’evento E diventa 2 su 6
Un evento di cui la probabilità è 0 è IMPOSSIBILE ( non ha nessun caso favorevole).
Un evento di cui la probabilità è 1 si dice CERTO.
0<P<1
Possibile
Si legge così:
P>o=a0
P<o=1
++++++++++++++++++++++++++++++++++++++++++++++++++
Le palline
B
V
R
R
V
B = bianca
R = rossa
V = verde
P = probabilità
In un sacchetto ci sono 6 palline.
R
Estraggo una pallina:
- ci sono 3 risultati possibili: può uscire bianca, verde o rossa.
P (1V) 2/6
P (1R) 3/6
P (1B) 1/6
++++++++++++++++++++++++++++++++++++++++++++++++++
EVENTO COMPLEMENTARE
(probabilità formulata come negazione)
Qual è la probabilità che non esca da un mazzo di 40 carte il fante di cuori (il fante di cuori
è 1 su 40) ?
La probabilità che non esca è:
1 – 1/40 = 39/40
(se prendo in considerazione una sola caratteristica)
Il fante di cuori corrisponde a 2 “eventi” infatti devo pescare 1 carta di cuori e che sia 1
fante.
Questi 2 eventi si possono verificare contemporaneamente perché esiste il fante di cuori
per cui sono EVENTI COMPATIBILI.
EVENTI INCOMPATIBILI
Se lancio 1 dado: qual è la probabilità che esca 1 numero dispari e > di 5 o minore di 1?
Si tratta di EVENTI INCOMPATIBILI.
La probabilità di eventi incompatibili è zero.