1.
Mani di poker
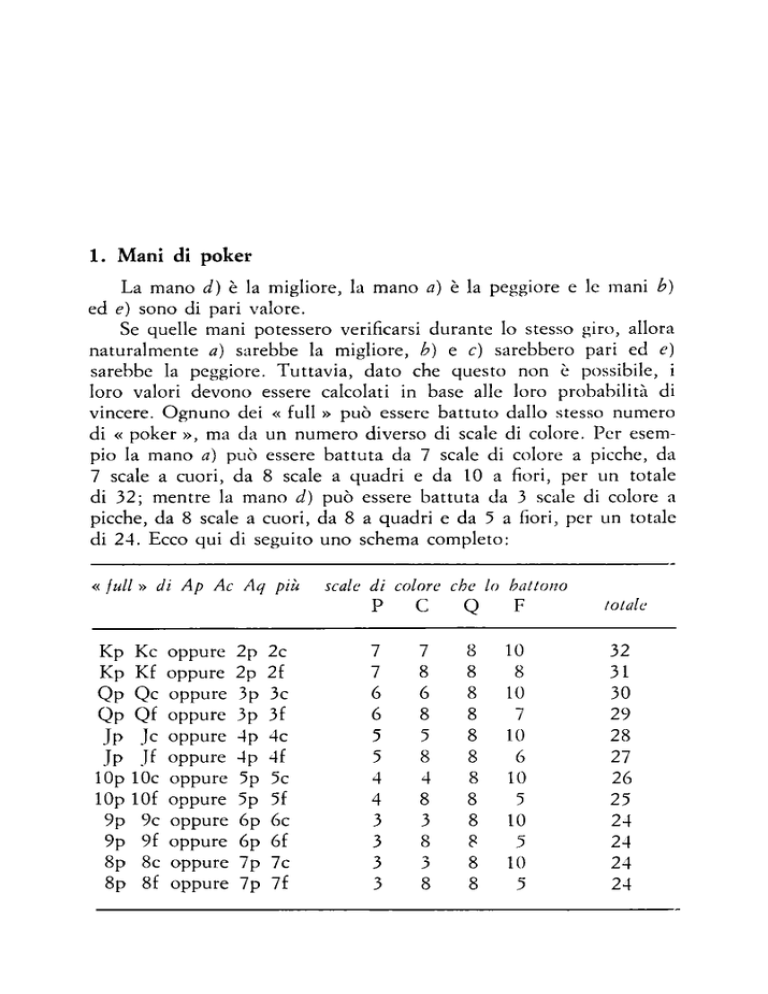
La mano d) è la migliore, la mano a) è la peggiore e le mani b)
ed e) sono di pari valore.
Se quelle mani potessero verificarsi durante lo stesso giro, allora
naturalmente a) sarebbe la migliore, b) e c) sarebbero pari ed e)
sarebbe la peggiore. Tuttavia, dato che questo non è possibile, i
loro valori devono essere calcolati in base alle loro probabilità di
vincere. Ognuno dei « full » può essere battuto dallo stesso numero
di « poker », ma da un numero diverso di scale di colore. Per esem­
pio la mano a) può essere battuta da 7 scale di colore a picche, da
7 scale a cuori, da 8 scale a quadri e da 10 a fiori, per un totale
di 32; mentre la mano d) può essere battuta da 3 scale di colore a
picche, da 8 scale a cuori, da 8 a quadri e da 5 a fiori, per un totale
di 24. Ecco qui di seguito uno schema completo:
« full » di Ap Ac Aq più
Kp Kc oppure
Kp Kf oppure
Qp Qc oppure
Qp Qf oppure
Jp Jc oppure
Jp Jf oppure
lOp lOc oppure
lOp lOf oppure
9p 9c oppure
9p 9f oppure
8p 8c oppure
8p 8f oppure
2p
2p
3p
3p
4p
4p
5p
5p
6p
6p
7p
7p
2c
2f
3c
3f
4c
4f
5c
5f
6c
6f
7c
7f
scale di colore che lo battono
F
P
C
Q
7
7
6
6
5
5
4
4
3
3
3
3
7
8
6
8
5
8
4
8
3
8
3
8
8
8
8
8
8
8
8
8
8
8
8
8
10
8
10
7
10
6
10
5
10
5
10
5
totale
32
31
30
29
28
27
26
25
24
24
24
24
44
GIOCHI DI MATEMATICA E LOGICA
2 . 100
cifre
La probabilità è zero. Se un numero ha n cifre, allora il suo
quadrato ha 2n o 2n-\ cifre. Quindi un numero più il suo quadrato
ha 3// o òn-\ cifre. Poiché 100 è della forma 3/2 + 1, è impossibile
formare un numero e il suo quadrato usando esattamente 100 cifre.
3. L’incontro di scacchi
Bianchi ha più del 53% di probabilità di vincere l’incontro.
La sua migliore strategia è quella di giocare d’attacco se è indietro
o in parità e di rimessa se è avanti. I possibili risultati e le loro
probabilità sono schematizzati sotto. V, Pa e Pd rappresentano le
vincite, i pareggi e le perdite di Bianchi.
(in attacco)
0,9X0,45
= 0,405
0,1X0,45
= 0,045
0,45X0,55
= 0,2475
0,55X0,55
= 0,3025
(perde l’incontro)
(vince rincontro)
totale = 0,2025
(in attacco)
V
Pd
0,45X0,2925
= 0,131625
0,55X0,2925
= 0,160875
(vince rincontro)
(perde l'incontro)
totale probabilità
0,536625
0,463375
vince l’incontro
perde l’incontro
4. Il numero telefonico del professore
Il numero di telefono del professore è 9899901, che equivale a
9X1099989. Altri numeri aventi questa caratteristica si possono
SOLUZIONI
45
formare inserendo dei 9 tra il 98 e lo 01, per esempio 98 01, 9890 1,
989901 e così via. Un altro numero di questo tipo è 8712 che
equivale a 4 X 2 1 7 8 . Infine altri numeri si possono formare ripe­
tendo i gruppi di base; per esempio:
9 8 9 9 9 0 1 9 8 0 1 9 8 9 9 0 1 = 9 X 10 99 8 9 1 0 8 9 1 0 9 9 9 8 9 .
5. Le case e i pozzi
6.
Quattro punti
Non c’è niente nella formulazione del problema che restringe
i punti ad un piano. Mario dispose i quattro punti agli angoli di
un tetraedro.
7. Il caso dello strano cubo
La faccia opposta al « sei » deve mostrare due puntini. La vista
del cubo aperto è mostrata sotto.
La maggior parte dei solutori arriva alla soluzione « uno ». La
ragione per la quale questa non è giusta è che il « due » e il « tre »
mostrati nella figura 1 non possono essere entrambe le stesse facce
GIOCHI DI MATEMATICA E LOGICA
46
mostrate nella figura 2. Se il cubo è tenuto in modo da formare
una « V » con il « due » e il « tre », allora il « due » è sulla si­
nistra nella figura 1 e sulla destra nella figura 2.
o o o
o o o
O
o
8.
Gli esagoni
Una volta capito che l’esagono non deve necessariamente es­
sere convesso, è facile trovare altre soluzioni simili a quella mo­
strata sotto.
9. Un numero insolito
Un numero che sia quadrato, cubo e quinta potenza deve essere
anche una 2 X 3 X 5 = 3 0 a potenza. 330 è qualcosa di molto più grande
di 200 000 000 000 000 quindi la soluzione deve essere 230 che è
uguale a 1 073 741 824.
1 0 . Testa
o croce?
a) Berto (16)
b) Carlo (20)
c) Alfredo (18)
Con un numero pari di lanci la possibilità di uscita dello stesso
numero di teste e croci riduce la probabilità che una esca più del­
SOLUZIONI
47
l’altra. Più alto è il numero di lanci pari, più bassa è la probabilità
dello stesso numero di teste e croci. Quindi ha meno probabilità
di avere più teste che croci quello col numero minore di lanci pari.
11.
Una partita a scacchi
Poiché si gioca a scacchi tenendo una casella bianca all’angolo
destro dei giocatori, questi dovevano essere alla destra e alla sini­
stra della scacchiera in figura. Quindi sia che il bianco muova verso
sinistra o verso destra, vince facendo Regina del suo Pedone: c7-c8
(Regina), matto.
12.
Padre e figlio
Umberto ha 3 anni e suo padre 51 (3X51 = 153).
13. Il giocatore
Ogni volta che lui punta 10 dollari sul rosso, lei ne punta 100
sul nero.
14. I cugini di Gianni
Gianni ha 43 anni ed i suoi cugini 2, 2 e 3 anni. Per ogni
altro valore dell’età di Gianni sarebbe esistita più di una combi­
nazione, ed il professore non avrebbe avuto dati sufficienti per
determinare l’età dei cugini.
Moltiplicazioni
927
58401
48
16.
GIOCHI DI MATEMATICA E LOGICA
402
39
15678
17.
715
46
32890
18.
297
54
16038
19.
594
27
16038
20 .
396
45
17820
21 .
345
78
26910
22.
367
52
19084
SOLUZIONI
49
495
17820
24. Tagli sulla scacchiera
25. Gioco scorretto
Il Detroit, il Boston ed una terza squadra, il New York, sono
in testa alla classifica a parità di punteggio. L’ultima partita del
Boston è contro il New York, mentre l’ultima del Detroit è contro
una delle altre squadre. Se il Detroit perde e il Boston vince, allora
il Boston ha vinto il campionato; mentre se vincé il Detroit, que­
st’ultimo termina in parità con il vincitore della partita BostonNew York.
26. Bollettino meteorologico
Le cinque temperature erano 1; — 1; 2; —2; 3.
50
GIOCHI DI MATEMATICA E LOGICA
27. Il prezzo del pranzo
Nel loro Stato, la tassa di vendita è di quattro cents per spese
da 76 cents a 1 dollaro e 10 cents, e di cinque cents per spese da
1 dollaro e l i cents a 1 dollaro e 35. Quindi non si potrà mai
avere un conto totale di 1 dollaro e 15 cents.
28. Cifre e potenze
92, = 1094 189 89 13 15 123 59209
Per valori di n maggiori di 21, 10" ha «4-1 cifre, mentre 9" ha
meno di n cifre.
29. Addizioni
Le due soluzioni
146
583
157
482
729
639
718
236
729
135
954
864
e
30. Ancora addizioni
Ci sono due soluzioni:
583
146
715
248
729
963
o
482
157
614
358
639
972
51
SOLUZIONI
31. I quadrati di Biagio
Il
ragionamento di Silvio contiene un’inesattezza. I quadratini
non compaiono lo stesso numero di volte nei sedici quadrati 2X2.
Ogni quadratino d’angolo compare una sola volta, i quadratini late­
rali compaiono due volte, mentre i quadratini interni compaiono
quattro volte. Quindi, il colore che compare di meno viene com­
pensato dalla sua maggiore presenza all’interno. Due soluzioni pos­
sono essere le seguenti:
32. Un sacchetto di biglie
C’è una probabilità di 2/3 che anche la seconda biglia sia color
porpora. Questo risultato è indipendente dal numero delle biglie
contenute nel sacchetto, e quanto segue ne è la prova.
Posto
numero delle biglie nel sacchetto, ognuna delle se­
guenti combinazioni n + 1 ha una probabilità di l/(/z+ l).
numero delle biglie arancioni
numero delle biglie porpora
0
1
2
n
n—1
n —2
n-k
k
n
0
52
GIOCHI DI MATEMATICA E LOGICA
In tutte le combinazioni descritte, ci sono un totale di n(n-\-ì)/2
biglie color porpora, ognuna delle quali ha la stessa probabilità,
2/n(n+\)y di essere estratta per prima, se quella estratta prece­
dentemente è stata specificata essere di color porpora. Quindi, la
probabilità che la prima biglia provenga da un sacchetto contenente
un numero k di biglie color porpora è 2k/n(n+ \). Dopo avere
estratto la prima, ci sono k— 1 biglie color porpora fra le n— 1
biglie restanti nel sacchetto, e le probabilità che la biglia estratta
sia ancora porpora è {k— 1)/(;?— 1). La probabilità che la prima bi­
glia color porpora provenga da quel sacchetto e che anche la seconda
biglia sia dello stesso colore è data dal prodotto delle singole pro­
babilità 2k[k— \)/n(n-\-\) (n— 1). La probabilità totale per ogni
possibile combinazione è dunque:
2{l/ò)(n-\)n(n+\)
n ( n + 1 ) (n — 1)
3
33. Ellissi
La più grande (ed unica) ellisse è la sponda del laghetto, che
racchiude l’area di cinquanta metri quadrati. Gli altri due ovali non
sono ellissi.
34. Un altro strano cubo
La faccia inferiore della figura 1, opposta alla faccia di colore
A, deve essere anch’essa di colore A.
35. La corsa allo scudetto
Le probabilità del Detroit di vincere il campionato sono circa
del 51%. La dimostrazione di questo curioso risultato è la seguente:
la probabilità del Detroit di vincere tutte e tre le partite per ag­
giudicarsi lo scudetto è 0,663= 0,287496. La probabilità del De­
troit di vincerne due e pareggiarne una è 3 X0,662X 0,34 = 0,444312.
Il restante 0,268192 rappresenta la probabilità del Detroit di per­
53
SOLUZIONI
dere due o tre partite, e quindi di perdere il campionato. In caso
di parità, il Detroit avrebbe la stessa probabilità dello 0,222156 sia
di vincere che di perdere lo spareggio. Quindi le probabilità totali
per il Detroit di vincere il campionato sono dello 0,509652.
36. Un gruppo di numeri
Non possono esserci più di cinquanta numeri interi nel gruppo,
altrimenti ci sarebbero alcune coppie la cui somma è 100. Ci sono
diverse soluzioni possibili con cinquanta numeri interi, la più sem­
plice delle quali è rappresentata dal gruppo di numeri interi da 50
a 99.
37. Due addizioni
286
286
286
3210
572
3496
38. Il vero ed il falso
La domanda del professore era: « Se io ti chiedessi, ‘un trian­
golo, ha quattro lati?’ la tua risposta sarebbe uguale alla risposta a
questa domanda? » Né una persona che dice sempre il falso, né
una che dice sempre il vero, potrebbero rispondere « Sì » o « No »
senza rompere la propria regola. Naturalmente alla domanda « un
triangolo, ha quattro lati? » si poteva sostituire qualunque altra
domanda la cui risposta esatta fosse « No ». Il professore avrebbe
anche potuto chiedere: « Se io ti domandassi, ‘un triangolo, ha tre
lati?’ la tua risposta sarebbe diversa dalla risposta a questa doman­
da? » ed ottenere lo stesso risultato.
39. Cinque pesi
Chiamiamo i pesi A, B, C, D ed E. Le prime tre pesate da
eseguire sono: 1) AB ** CD; 2) AC ** BD; 3) AD BC.
CICCHI DI MATEMATICA E LOGICA
54
Possono verificarsi tre casi diversi:
I. Nessuna delle prime tre pesate sta in equilibrio, e c’è uno
dei pesi (per es. A) che è sempre sul lato più pesante:
CD
1)
/
AB
2)
BD
/ ■
AC
BC
3)
/
AD
Quindi A = 5 g ed E = 4 g. Le due pesate successive sono:
4) B ~ C ;
5) E ~ B C .
Presumendo che, diciamo, B si dimostri più pesante di C nella
quarta pesata, allora i risultati della quinta pesata possono essere
i seguenti:
BC
/
E
E
\
E—BC
B= 2
C= 1
D=3
BC
3
1
2
3
2
1.
II. Nessuna delle prime tre pesate sta in equilibrio, e c’è un
peso (per es. A) che è sempre sul lato più leggero:
D
AB
\
AC
; 2)
CD.
AD
\
; 3)
BD.
\
.
BC
Quindi A =1 g ed E = 2 g. La pesata seguente è: 4) B C.
Presumendo che, diciamo, B si dimostri più pesante di C, al­
lora la pesata finale è: 5) B «-» AD, ed i suoi risultati saranno:
AD
/
B
B= 5
C= 4
D= 3
B
B—AD
\
AD
5
3
4
4
3
5.
55
SOLUZIONI
III.
Una delle pesate (per es. la n. 1) sta in equilibrio: nelle
altre due pesate uno dei pesi è sempre sul lato più pesante (per
es. A) ed uno dei pesi è sempre sul lato più leggero (per es. B):
BD
BC.
2)/ ;3)/
1) AB—CD;
AC
AD
La pesata successiva è: 4) C D.
Presumendo che, diciamo, C sia più pesante di D, la pesata
finale è: 5) E ** BD, dalla quale avremo:
BD
/
E
A= 4
B=1
C= 3
D= 2
E= 5
E
E—BD
5
1
4
2
3
\
BD
5
2
4
3
1.
40. Il minor numero di tentativi
Ci sono 5! = 120 possibili combinazioni dei cinque pesi. Ogni
pesata divide le possibilità in uno dei tre casi: lato sinistro più
pesante; lato destro più pesante; oppure equilibrio di entrambi i
lati. Anche con il più perfetto sistema per ripartire le possibilità
nei tre casi, non più di 3n possibilità iniziali possono essere ridotte
ad una singola possibilità in n pesate.
Poiché 34= 81 e 35= 243, occorrono come minimo cinque pe­
sate per determinare quale delle 120 possibilità iniziali è quella
giusta.
Altre addizioni
56
GIOCHI DI MATEMATICA L LOGICA
437
42.
589
1026
43.
426
879
1305
44.
246
789
1035
45.
624
879
1503
46.
264
789
1053
47.
743
859
1602
48.
473
589
1062
SOLUZIONI
57
4
49.
35
987
1026
50.
3
45
978
1026
51.
3
74
985
1062
52. Un’altra partita a scacchi
La chiave di questo problema sta nel considerare le mosse che
hanno potuto portare alla situazione raffigurata. Il nero non può
avere appena mosso il proprio Re. Se il Re fosse stato mosso da
qualunque altra posizione, sarebbe già stato sotto scacco prima an­
cora delPultima mossa del bianco. Non ha potuto muovere il pro­
prio Alfiere o i tre Pedoni dalle loro posizioni iniziali. Non è
possibile che il Pedone nero in c5 sia stato mosso da c6 perché
altrimenti il bianco sarebbe stato sotto scacco, e non può esserci
arrivato mangiando un pezzo. L’unica mossa possibile che il nero
ha potuto fare è stata c7-c5. Quindi il bianco vince con b5Xc5
(en passant), matto.
53. Il quadrato perfetto
L’ultima cifra o coppia di cifre di un quadrato perfetto deve
essere 1, 4, 6, 9, 25 oppure 00. La somma di tutte le cifre deve
58
GIOCHI DI MATEMATICA E LOGICA
essere 1, 4, 7 oppure 9. (Se il risultato contiene più di una cifra,
sommate ancora le cifre e ripetete l’operazione finché non risulti
una sola cifra).
Tutto questo elimina i primi quattro numeri e quindi il qua­
drato perfetto deve essere stato il quinto numero, completamente
perduto.
54. Uno strano attrito
L’oggetto è in orbita. L’attrito con l’atmosfera ne causa la ca­
duta verso un’orbita più bassa, dove la velocità orbitale è più ele­
vata. La diminuzione dell’energia potenziale compensa sia l’au­
mento di velocità che la perdita di energia dovuta all’attrito.
55. Gli angoli
Andrea ha fatto prima l’angolo B, ed ha poi costruito l’angolo
À tre volte più grande.
56. La mano migliore
Come nel problema n. 1, le mani non possono presentarsi du­
rante lo stesso giro, e quindi il loro valore deve essere calcolato in
base alle loro probabilità di vittoria. Ogni « full » può essere bat­
tuto dallo stesso numero di « poker », ma da un numero diverso
di scale di colore. La mano a) può essere battuta da 32 scale di
colore (7 scale di picche, 7 scale di cuori, 8 di quadri e 10 di fiori),
mentre la mano b) può essere battuta soltanto da 31 scale di co­
lore (7 scale di picche, 8 scale di cuori, 8 di quadri e 8 di fiori).
Quindi la mano b) è migliore.
57. Parallelepipedi pitagorici
Si deve semplicemente sostituire il primo esempio di triangolo
pitagorico (32+ 42= 52) nel secondo esempio (52+ 122= 132) per ot­
tenere 32+ 42+ 122= 132.
59
SOLUZIONI
58. Il cubo bicolore
Nel disegno potete vedere lo sviluppo dei due cubi. Per qua­
lunque faccia tenuta in posizione superiore, lo schema formato dal­
le altre facce è sempre lo stesso.
L
À
59. Il campionato di baseball
Perché, a causa dei rinvii, il Washington ha ancora abbastanza
partite da giocare per raggiungere il New York in testa alla classifi­
ca, vincendole tutte, ed avrebbe la possibilità di battere il New York
60
GIOCHI DI MATEMATICA E LOGICA
in uno spareggio. Il Detroit, pur essendo davanti al Washington in
percentuale, è stato già eliminato. Per esempio, la situazione po­
trebbe essere la seguente:
N.Y.
D.
W.
vittorie
sconfitte
%
108
106
104
54
55
54
0,6667
0,6584
0,6582
partite di
svantaggio
_
Wi
2
partite da
giocare
0
1
4
60. La roulette
Il tranello è che nei casi in cui non conta il numero delle
vincite e delle perdite, allora la somma di denaro che verrebbe
perduta nelPeventualità di un numero apprezzabilmente alto di per­
dite sarebbe più grande della somma vinta nella eventualità di un
equivalente numero apprezzabilmente alto di vincite. Se consideria­
mo tutte le possibili uscite di un dato numero di puntate, la media
è data dalla normale percentuale di vincite del banco. Il « sistema »
avrebbe potuto considerare anche altre percentuali che non fossero
del 20%. Se per esempio fosse stato usato il 100%, avremmo
avuto il ben noto espediente di raddoppiare la puntata ad ogni
perdita.
61. L’anello numerato
Le quattro soluzioni sono:
a)
b)
c)
d)
1
1
1
1
3 5 7 9 11 2 4 6 8 10
4 7 10 2 5 8 11 3 6 9
5 9 2 6 10 3 7 11 4 8
6 11 5 10 4 9 3 8 2 7
È interessante notare che anche ogni coppia di soluzioni sod­
disfa alle condizioni poste dal problema.
61
SOLUZIONI
62. La partita di poker
Il professore rispose che la mano di Gino, con il « poker », era
la peggiore. La «scala reale» di Gianni avrebbe avuto la meglio
su tutti gli altri avversari, e quindi la mano peggiore è da con­
siderare quella che ha le maggiori probabilità di perdere la più
alta somma di denaro. Giorgio, Giacomo e Giuseppe hanno dei
punti molto bassi ed è probabile che passino dopo le prime puntate:
dunque è Gino ad avere la probabilità maggiore di perdere molto
più degli altri.
A ltre moltiplicazioni
63.
1 X 26 X 345 = 8970
64.
2 X 1 4 X 3 0 7 = 8596
65. L’area della corona circolare
Congiungendo i punti A e B con il centro del cerchio si ottiene
un triangolo rettangolo. Posto che ri = raggio della circonferenza in­
terna ed = raggio della circonferenza esterna, applicando il teo­
rema di Pitagora si ottiene che r i — r \ —2.
62
GIOCHI DI MATEMATICA E LOGICA
L’area della corona circolare è data dalla formula itir2—r 2).
Poiché il termine tra parentesi è uguale a 2, l’area della corona cir­
colare è 2 tz centimetri quadrati.
66.
Ancora sul vero e sul falso
La domanda è: « Queste affermazioni sono entrambe vere?
a) Tu sei del tipo A.
b) Se la domanda fosse “Un triangolo, ha quattro lati?” la
tua risposta sarebbe stata uguale a quella di questa domanda ».
In risposta a questa domanda, il tipo V risponderà « No »;
il tipo F risponderà « Sì »; e il tipo A sarà incapace di rispondere.
67. Il roseto di Rosetta
68.
La decima potenza
Il metodo più semplice consiste nel notare che soltanto due
numeri di dieci cifre sono una decima potenza: 810 e 910. Inoltre, per
mezzo della « prova del nove », si scopre che un numero composto
di dieci cifre diverse deve essere un multiplo di 9, così che resta
SOLUZIONI
63
da considerare soltanto 910. Dopo aver calcolato 910 vediamo che
il risultato contiene diverse cifre ripetute, e quindi è verificata
l’ipotesi che tale numero non esiste.
69. I trucchi di Bruno
a) Nel mazzo originale c’erano trenta carte.
b) Quando il trucco è stato ripetuto con 32 carte, l’ordine
finale dellfc carte è risultato essere l’inverso dell’ordine originale.
Ancora un p o ’ di moltiplicazioni
297
70.
«
5346
483
71.
12
5796
72.
138
42
5796
73.
157
28
4396
74.
186
39
7254
64
GIOCHI DI MATEMATICA E LOGICA
159
48
75.
7632
198
27
76.
5346
77.
Ai grandi magazzini
Mentre lei aspettava che il professore la trovasse nel reparto dei
cappellini, lui, seguendo lo stesso ragionamento, stava aspettando
che lei lo trovasse nel reparto libri.
78. Su mezza scacchiera
L’ordine originale delle file era d), a), b), c)\ e il numero che
originariamente si trovava nella terza fila era 26382629.
Perché un numero possa dirsi divisibile per 11 è necessario
che dia un risultato, le cui cifre sommate e sottratte alternativamente diano ancora un numero divisibile per 11. I colori delle
caselle identificano le cifre alterne, dalle quali si vede che c) è
l’unico numero divisibile per 11, indipendentemente dal loro or­
dine. I numeri a) e c) sono gli unici che contengono un 5 o uno 0.
Poiché c) è già stato identificato come il numero divisibile per 11,
a) deve essere quello divisibile per 5. Dalla somma delle cifre si vede
che a) e d) sono divisibili per 3. Poiché a) è già stato identificato
come il numero divisibile per 5, d) deve essere il numero della prima
fila in alto. Quindi l’ordine dei numeri è d)} b), c). Poiché a) termina
con una casella nera, 0, allora b), il numero divisibile per 7, deve
terminare con una casella bianca. Ci sono 48 combinazioni possibili,
ma l’unica divisibile per 7 è 26382629.
65
SOLUZIONI
79. Il torneo di scacchi
Carlo ha il 32,4% di probabilità di vincere il torneo, contro il
28% di probabilità di Alessio. Questo risultato paradossale è dimo­
strato dal seguente schema:
risultati
A-B
A-C
punteggio
(il vincitore
è in neretto)
B-C
A
1
1
1
1
1/2
1/2
1/2
1/2
0
0
0
0
1/2
1/2
1/2
1/2
1
1
1/2
1/2
1
1
1/2
1/2
0
0
1/2
1/2
0
0
1/2
1/2
1
0
1
0
1
0
1
0
0
1
0
1
0
1
0
1
B
2
2
IV2
IV2 *
IV2 *
C
1
0
1
0
0
1
1/2
172
0
1
1/2
IV2
1/2
1
1
1/2
IV2
probabilità
IV2
IV2
(0,1)
(0,1)
(0,1)
(0,1)
(0,9)
(0,9)
(0,9)
(0,9)
(0,2)
(0,2)
(0,8)
(0,8)
(0,2)
(0,2)
(0,8)
(0,8)
(0,55)
(0,45)
(0,55)
(0,45)
(0,55)
(0,45)
(0,55)
(0,45)
=
=
=
=
=
=
=
=
0,011
0,009
0,044
0,036
0,099
0,081
0,396
0,324
* Significa che vince lo spareggio.
80. La serratura
La traccia da scoprire consisteva nel fatto che l’affermazione del
guardiano era letteralmente vera. Alla velocità di un numero al
secondo, impiegherebbe effettivamente cento anni per arrivare alla
combinazione giusta. Il prigioniero calcolò che in cento anni ci
sono 3155760000 secondi, ed è questo il numero che provò a
comporre.
81. Alberi
La seguente disposizione mostra come, per mezzo di una com­
binazione di spazi a forma di quadrato e di triangolo equilatero,
il contadino sia riuscito a piantare ben 128 alberi nel proprio campo.
66
GIOCHI DI MATEMATICA E LOGICA
82. Una frazione da semplificare
Ci sono due soluzioni:
1666666666
1
1999999999
1
--------------- — — oppure ---------------- = —
6666666664
4
9999999995
5
Il risultato non cambia, purché ci sia sempre lo stesso numero
di 6 o di 9 sia al numeratore che al denominatore.
67
SOLUZIONI
83. La palla di Gianni
La soluzione è quella che potete vedere qui sotto. Vengono
indicate le sezioni trasversali attraverso il centro della sfera.
I tagli sono simmetrici intorno all’asse verticale.
b (bianco)
n (nero)
84. Ancora baseball
Una squadra deve giocare almeno 107 partite per poter avere
una media dello 0,664. Con un numero inferiore di partite la media
sarà maggiore o minore di 0,664, ma mai esattamente 0,664 con
tre cifre decimali. Con 107, o più, partite giocate ed una media
dello 0,664, la squadra deve averne vinte 71 o più. Quindi le
« Tigri » sono in testa rispetto agli « Yankees ».
85. Il sistema solare
Il pianeta solitamente più vicino a Plutone è Mercurio. Notate
che la domanda non era « Quale pianeta si avvicina di più a Plu­
tone? » oppure « L’orbita di quale pianeta è più vicina a quella di
Plutone? ».
68
GIOCHI DI MATEMATICA E LOGICA
Il
disegno indica le orbite di Plutone e di Mercurio, e l’orbita
di un qualunque pianeta intermedio, per esempio la Terra. Se con­
sideriamo Plutone immobile, la sua velocità angolare può essere
sottratta da quella di ognuno degli altri pianeti.
Tracciamo la linea PS fra Plutone (P) ed il Sole (S), e la linea
TS perpendicolare a PS, e consideriamo due brevi tratti uguali del­
l’orbita di Mercurio, Ax e Ax’ rispettivamente, equidistanti da TS:
l’Arco A y è più lungo dell’arco A.
Se £ è la circonferenza dell’orbita della Terra, durante il tempo
in cui Mercurio si trova in A x’, la Terra è più lontana da Plutone
se è su A* e più vicina se è su E-A1; cioè la probabilità è A'/E che
sia più lontana da Plutone ed (E-Ay)/E che sia più vicina. Allo
stesso modo, nel momento in cui Mercurio si trova in Ax, la pro­
babilità è (E-A)/E che la Terra sia più lontana da Plutone, e A /E
che sia più vicina. Quindi, sia che Mercurio si trovi in Ax, sia che
si trovi in A x’ la probabilità è [A’+ E —A)/2E che la Terra sia
più lontana da Plutone, e (E —A ’-\-A)/2E che sia più vicina. Poiché
A } è più lungo di A, c’è una probabilità maggiore che la Terra sia
più lontana da Plutone di Mercurio, di quanto sia più vicina nel
momento in cui Mercurio è entro i segmenti Ax e A x’. Poiché l’or­
bita di Mercurio può essere completamente suddivisa in coppie di
segmenti come Ax e A x’, e poiché ognuno degli altri pianeti può
essere sostituito alla Terra nella precedente dimostrazione, si può
69
SOLUZIONI
concludere che Mercurio è più vicino a Plutone un numero maggiore
di volte rispetto a qualunque altro pianeta.
86.
Numeri esagonali
In realtà le quotazioni erano 2 a 1 in favore dell’estrazione
di un numero esagonale. Biagio scelse le cifre 1, 2 e 7. Delle sei
possibili combinazioni di queste cifre, le quattro dispari sono nu­
meri esagonali (notate che tutti i numeri esagonali sono dispari):
127 (n = 6), 217 (» = 8), 271 (* = 9) e 721 («=15).
È interessante notare che i due numeri dispari scelti da Biagio,
1 e 7, sono anch’essi numeri esagonali.
87. La temperatura dell’acqua
La chiave di questo gioco sta nell’avere i due serbatoi K e I
raffigurati nel disegno a 0 °C. Se la pressione è tale da dare un
L
b -<*
il il
T = 40°
P = 5
K
b ^
Il II
J
M
T = 80°
P = 5
-
R=1
R = 1
flusso= 0 da questi due serbatoi quando entrambe le valvole sono
aperte, allora per ogni combinazione di temperatura, pressione e
resistenza nel resto del sistema, la temperatura risultante sarà data
da ( T a + T b ) / 2 . I disegni successivi mostrano quali valvole sono
70
GIOCHI DI MATEMATICA E LOGICA
aperte di volta in volta. I valori indicati nel primo disegno sono
un esempio di come si può arrivare alla soluzione desiderata, mentre
gli altri disegni indicano i flussi risultanti e le temperature ottenute.
A aperto B chiuso
T = 20
A chiuso B aperto
T = 40
A e B aperti
T = 60
88.
Il consulente del lavoro
Mario veniva considerato il loro miglior impiegato. Essi facevano
semplicemente il contrario di ciò che lui suggeriva, e ne ricavavano
notevoli profitti.
SOLUZIONI
71
89. Il divisore
Una soluzione è: >4=1; J3 = ll! + 1.
90. Il cono
Se uno dei tagli fosse stato fatto attraverso l’intero cono, la
parte indicata con A sarebbe stata identica ad A \ Il taglio forma
un’ellisse il cui asse maggiore è rappresentato dal segmento che va
da e ad e . Quindi le facce E della parte superiore e di quella in­
feriore coincidono.
91. Il filantropo
Anche de’ Guadagnis si era impegnato in tal senso. Quindi se
una terza persona avesse offerto anche soltanto un cent, Soldoni e
de’ Guadagnis avrebbero potuto versare tutto il loro patrimonio
nel tentativo di uguagliare l’uno il contributo dell’altro, più un cent.
92. Caccia al numero
A e An non possono avere un totale di m{n + 1) + 1 cifre, dove
w è un qualunque numero intero. Quindi, per 21 cifre, n non può
essere 1, 3, 4 oppure 9. I valori di n per i quali la somma delle
cifre può essere uno, sono 1, 3, 7 oppure 9. Poiché 1, 3 e 9 sono
stati esclusi, n è 7.
72
GIOCHI DI MATEMATICA E LOGICA
93. La raccolta delle mele
Il
numero dei compratori deve essere un divisore di 314827 +
1199533 = 1514360, e di 314827 + 683786 = 998613. Il massimo
comun divisore di quei due numeri è 131. Poiché 131 è un numero
primo, ci sono 131 compratori.
94. Un duello a tre
Adottando la seguente strategia, la probabilità di Alessandro di
sopravvivere rasenta la certezza!
Alessandro fa questa affermazione: « Se Bartolomeo è d’accordo
ad uccidere Cesare, allora mi comporterò così:
a) Se sparo per primo, sbaglierò il colpo.
b) Se Bartolomeo sparerà per primo, allora io colpirò Bar­
tolomeo con una probabilità dello 0,9999 e lo mancherò con una
probabilità dello 0,0001.
c) Se Cesare spara per primo e colpisce Bartolomeo, allora io
colpirò Cesare con una probabilità dello 0,9999 e lo mancherò con
una probabilità dello 0,0001. Se Cesare sbaglia, allora sbaglierò an­
ch’io.
Se Bartolomeo afferma qualunque altra cosa che non sia spa­
rare a Cesare, e quindi se Cesare è d’accordo a sparare a Bartolomeo,
io sparerò a Bartolomeo, oppure sbaglierò il colpo se Bartolomeo
è già stato colpito. Se Cesare non èd’accordo a sparare a Bartolo­
meo, allora io sparerò a Cesare ».
A causa dell’affermazione di Alessandro, Bartolomeo sarà d’ac­
cordo a sparare a Cesare, e Cesare, se sparerà perprimo, sparerà
a Bartolomeo. Bartolomeo e Cesare avranno ciascuno unaprobabi­
lità di sopravvivere dello 0,00003 ed Alessandro dello 0,99993.
Bartolomeo sarà d’accordo a sparare a Cesare perché altrimenti
non avrà nessuna probabilità di sopravvivere. Quindi, se Bartolomeo
non è d’accordo a sparare a Cesare, allora Cesare avrà almeno 2/3
di probabilità di sopravvivere accordandosi per uccidere Bartolomeo,
mentre ne avrà meno di 2/3 facendo qualunque altro accordo che
dia a Bartolomeo qualche possibilità di sopravvivere.
Se Cesare sparerà per primo, sparerà a Bartolomeo, poiché al­
trimenti non avrà nessuna possibilità di sopravvivere.
73
SOLUZIONI
I risultati di questo problema sono degni di nota, in quanto
sarebbe semplice concepire un accordo tale che, per esempio, Barto­
lomeo e Cesare avessero ciascuno il 50% di probabilità di soprav­
vivere, mentre Alessandro non ne avrebbe nessuna. Comunque,
per quanto Bartolomeo e Cesare possano desiderare tale accordo,
per loro è impossibile realizzarlo.
95.
7 + 8 = 12
69298
90431 oppure
159729
85254
50671 oppure
135925
63732
39841
103573
96. I presidenti
Se il quinto presidente non fosse stato tra quelli che morirono in
quella data, allora l’articolo del giornale avrebbe sicuramente detto
che « Tre dei primi quattro presidenti morirono il quattro di luglio ».
Di conseguenza il professor Flugel aveva ragioni sufficienti per poter
affermare che il quinto presidente, James Monroe, morì in quella
data.
97. Una gara a tre
II Detroit ha circa il 31,39% di probabilità di vincere il cam­
pionato, in confronto al New York che ne ha il 30,25%. La ra­
gione di ciò è che il New York deve vincere due partite per ag­
giudicarsi il campionato, mentre al Detroit basta vincerne una, se
il Neu York perde la sua prima partita. Questo compensa abbon­
dantemente le migliori possibilità che il New York ha nelle singole
partite.
98. Le città
Le possibilità sono del 100%. Prendendo la circonferenza della
Terra come 25000 miglia, Crupnik è in qualunque luogo da zero
a 7000 miglia da Aardvosk.
GIOCHI DI MATEMATICA E LOGICA
74
99. Ancora un po’ di vero e falso
Il
professor Flugel fece la seguente domanda: « Se io ti chie­
dessi, ‘Come ti chiami?’ e la verità o la falsità della tua risposta
fossero le stesse rispetto alla tua risposta a questa domanda, quale
possibile risposta potresti darmi? ».
L’unico modo in cui l’abitante avrebbe potuto mentire o dire
la verità nella sua risposta, sarebbe stato dare il proprio nome;
ogni altra risposta non sarebbe stata né vera né falsa.
Supponiamo per esempio che abbia deciso di mentire. Se gli
veniva chiesto « Come ti chiami? » e fosse stato ancora deciso
a mentire, poteva dare qualsiasi altra risposta che non fosse il suo
nome. Quindi per mentire in risposta alla domanda del professor
Flugel, l’unica risposta possibile sarebbe stata il proprio nome.
D’altra parte, se aveva deciso di dire la verità, allora la sua
risposta sarebbe stata ugualmente la verità rispetto alla domanda
« Come ti chiami? », e sarebbe stata ancora il suo nome.
100. Il tredici fortunato
Ogni numero ha le seguenti caratteristiche:
a) se la cifra fi-allora Nm avrà la stessa cifra finale se w è
naie di N è
della forma
0
1
n (cioè, ogni valore)
n
2
4 /2 + 1
3
4
4w + l
2/2 + 1
n
5
6
7
72
4/2 +
8
4 /2 + 1
9
2/2+1
1
75
SOLUZIONI
Il
tredici appartiene a tutte le forme ny 2n + \ e 4/z+l e quindi
N13 ha sempre la stessa cifra finale di N.
b) se la somma
delle cifre di
N è
1
2
4
5
7
8
9
allora la somma delle cifre di Nm sarà la
stessa se w è della forma
n
Gn 4“ 1
òli + 1
6^+ 1
3n-r 1
2n + 1
n
La somma delle cifre è 9 se la somma delle cifre di N è 3 o 6
ed m b maggiore di 1. Poiché 13 e 31 sono entrambi della forma
n, 2w + l, 3« + l e 6/z+l, N13 ed N31 avranno entrambi la stessa
somma delle cifre di N, a meno che la somma delle cifre di N sia
3 o 6, nel qual caso la somma delle cifre di N13 e di N31 sarà 9.
c)
Il teorema di Fermat (da non confondere con « l’ultimo
teorema di Fermat » — vedere al riguardo un qualunque testo di
teoria dei numeri) afferma che Nn- N è divisibile per p se p è un
numero primo. Quindi, dato che 13 è un numero primo, N13—N è
divisibile per 13 per ogni valore di N.












