ANNO SCOLASTICO 2014/2015
DATA: 02.03.2015
CLASSE 2 B ELE
fila A
VERIFICA DI MATEMATICA
1. Risolvi le equazioni seguenti, senza applicare la formula risolutiva:
2. Risolvi le equazioni seguenti, applicando la formula risolutiva:
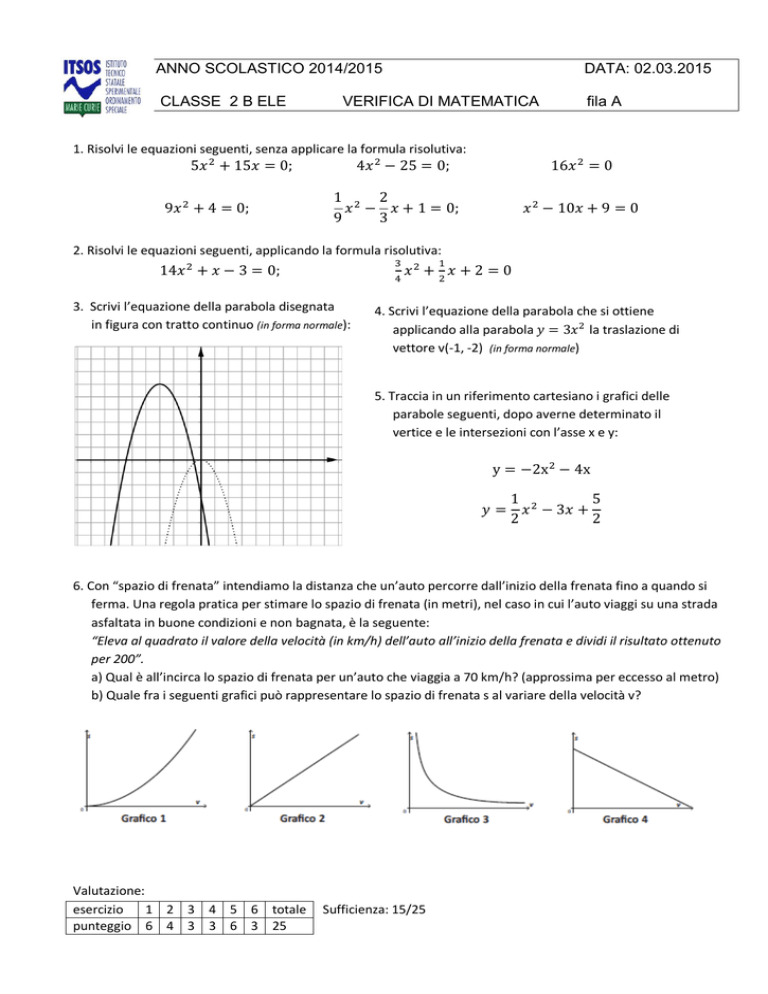
3. Scrivi l’equazione della parabola disegnata
in figura con tratto continuo (in forma normale):
4. Scrivi l’equazione della parabola che si ottiene
applicando alla parabola
la traslazione di
vettore v(-1, -2) (in forma normale)
5. Traccia in un riferimento cartesiano i grafici delle
parabole seguenti, dopo averne determinato il
vertice e le intersezioni con l’asse x e y:
6. Con “spazio di frenata” intendiamo la distanza che un’auto percorre dall’inizio della frenata fino a quando si
ferma. Una regola pratica per stimare lo spazio di frenata (in metri), nel caso in cui l’auto viaggi su una strada
asfaltata in buone condizioni e non bagnata, è la seguente:
“Eleva al quadrato il valore della velocità (in km/h) dell’auto all’inizio della frenata e dividi il risultato ottenuto
per 200”.
a) Qual è all’incirca lo spazio di frenata per un’auto che viaggia a 70 km/h? (approssima per eccesso al metro)
b) Quale fra i seguenti grafici può rappresentare lo spazio di frenata s al variare della velocità v?
Valutazione:
esercizio
1 2 3 4 5 6 totale
punteggio 6 4 3 3 6 3 25
Sufficienza: 15/25
ANNO SCOLASTICO 2014/2015
DATA: 02.03.2015
CLASSE 2 B ELE
fila B
VERIFICA DI MATEMATICA
1. Risolvi le equazioni seguenti, senza applicare la formula risolutiva:
2. Risolvi le equazioni seguenti, applicando la formula risolutiva:
3. Scrivi l’equazione della parabola disegnata
in figura con tratto continuo (in forma normale):
4. Scrivi l’equazione della parabola che si ottiene
applicando alla parabola
la traslazione di
vettore v(3, 1) (in forma normale)
5. Traccia in un riferimento cartesiano i grafici delle
parabole seguenti, dopo averne determinato il
vertice e le intersezioni con l’asse x e y:
6. Con “spazio di frenata” intendiamo la distanza che un’auto percorre dall’inizio della frenata fino a quando si
ferma. Una regola pratica per stimare lo spazio di frenata (in metri), nel caso in cui l’auto viaggi su una strada
asfaltata in buone condizioni e non bagnata, è la seguente:
“Eleva al quadrato il valore della velocità (in km/h) dell’auto all’inizio della frenata e dividi il risultato ottenuto
per 200”.
a) Qual è all’incirca lo spazio di frenata per un’auto che viaggia a 70 km/h? (approssima per eccesso al metro)
b) Quale fra i seguenti grafici può rappresentare lo spazio di frenata s al variare della velocità v?
Valutazione:
esercizio
1 2 3 4 5 6 totale
punteggio 6 4 3 3 6 3 25
Sufficienza: 15/25












