CAPITOLO SETTIMO
PROPRIETA’ TERMOFISICHE
DELLE SOSTANZE
Sostanze che compongono un sistema termodinamico
Un sistema termodinamico può essere composto nei modi più disparati, ma è
chiaro che le difficoltà, concernenti una indagine su di esso, crescono in
relazione anche alla sua composizione.
Pertanto, in ordine di difficoltà crescenti si possono classificare:
a) sistemi ad un unico componente chimico,
b) sistemi a due componenti fra di loro non affini,
c) sistemi a due componenti con affinità fisiche o chimiche,
d) sistemi più complessi.
Cap. 7
Pagina 1 di 25
Sistemi ad un unico componente – Sostanze pure
Un unico composto chimico (una miscela uniforme può rientrare in questa
categoria entro limitati campi di pressione e di temperatura), stabile per
qualsiasi valore di pressione e di temperatura entro il campo di indagine ed
uniformemente distribuito entro il volume di controllo, rappresenta il sistema ad
unico componente.
Una sostanza pura può trovarsi in uno dei seguenti stati di aggregazione:
a) stato solido caratterizzato da un definito volume e da una definita
forma,
b) stato liquido caratterizzato da un definito volume ma da una forma
corrispondente al contenitore che la racchiude,
c) stato aeriforme nel quale forma e volume dipendono dal
contenitore; lo stato aeriforme si distingue in stato di vapore (quando è
possibile far avvenire la condensazione operando sulla sola temperatura a
pressione costante) ed in stato di gas; nel caso di gas molto rarefatti le
equazioni di stato e di alcune trasformazioni sono molto vicine ad una
formulazione matematica semplice ed in tal caso si parla di gas ideali.
Ogni stato termodinamico è univocamente definito dalla conoscenza dei
valori di due grandezze intensive o specifiche, chiamate variabili o grandezze
di stato, fra loro indipendenti, come ad esempio pressione e temperatura,
pressione e volume specifico, pressione ed entalpia, ecc...
I cambiamenti da uno stato di aggregazione ad un altro vengono chiamati
come segue:
Cap. 7
1) liquefazione
passaggio da solido a liquido
2) solidificazione
passaggio da liquido a solido
3) evaporazione
passaggio da liquido a vapore
4) condensazione
passaggio da vapore a liquido
5) sublimazione
passaggio da solido a vapore
6) solidificazione
passaggio da vapore a solido
Pagina 2 di 25
A ciascuni di tali passaggi è associata una quantità di calore, perfettamente
definita per una stabilita situazione a cui avviene il passaggio (ad esempio
stabilita pressione); tale quantità di calore ha esattamente lo stesso valore
assoluto per passaggio diretto ed inverso, ma il segno è opposto.
Si avrà quindi:
1) calore di liquefazione uguale ma di segno opposto al calore di
solidificazione,
2) calore di evaporazione uguale ma di segno opposto al calore di
condensazione,
3) calore di sublimazione uguale ma di segno opposto al calore di
solidificazione.
I cambiamenti di stato sono pertanto trasformazioni reversibili.
Diagramma di stato pressione – volume specifico –
temperatura
Nel caso di sistema monocomponente lo stato termodinamico è stabilito da
una coppia di grandezze fra loro indipendenti; si può, seguendo la prassi più
ricorrente, considerare la pressione e la temperatura (nessuno impedisce di
scegliere temperatura e volume specifico o un’altra coppia).
Pertanto una qualsiasi altra grandezza di stato, ad esempio il volume
specifico, presenta un valore ben definito per ogni coppia di valori di pressione
e di temperatura; analiticamente questa condizione si esplicita scrivendo che v è
una funzione di p e T :
v= f p , T ,
ovvero, ancora più genericamente:
f v , p , T =0 .
Cap. 7
Pagina 3 di 25
Questa espressione, rappresentata graficamente, corrisponde ad una
superficie nello spazio cartesiano p, T e v ; nelle figure 7.1a, 7.1b e 7.2a e 7.2b
sono sono indicate, in forma assonometrica, tali superfici, per due diversi tipi di
sostanze, con le proiezioni su due piani cartesiani.
Le figure assonometriche anche se dimostrativamente valide, non sono però
di facile lettura numerica e pertanto vengono sostituite con diagrammi piani p T nei quali sono riportate curve parametriche per vari valori di v, chiamate
quindi curve isocore (vedi figura 7.3); queste curve sono, la proiezione di
sinistra del diagramma spaziale di figura 7.2.
Cap. 7
Pagina 4 di 25
Figura 7.1a – Vista assonometrica della superficie f p , v ,T =0
sostanze qualsiasi ad eccezione di sostanze a comportamento polare.
Cap. 7
Pagina 5 di 25
per
Figura 7.1 b – Vista assonometrica della superficie f p , v ,T =0
sostanze qualsiasi ad eccezione di sostanze a comportamento polare.
Cap. 7
Pagina 6 di 25
per
Figura 7.2a – Vista assonometrica della superficie f p , v , T =0 per
sostanze qualsiasi a comportamento polare (acqua, Ge, Bi, Ga, B2O3 ,..); si nota
che il solido presenta volume specifico maggiore di quello del liquido (il
ghiaccio immerso nell’acqua galleggia).
Cap. 7
Pagina 7 di 25
Figura 7.2 b – Vista assonometrica della superficie f p , v ,T =0 per
sostanze qualsiasi a comportamento polare (acqua, Ge, Bi, Ga, B2O3 ,..); si nota
che il solido presenta volume specifico maggiore di quello del liquido (il
ghiaccio immerso nell’acqua galleggia).
Cap. 7
Pagina 8 di 25
Figura 7.3 – Diagramma p (in ordinate) ,T (in ascisse) con le curve
parametriche a v=cost (isocore) per l’acqua.
Dalla costituzione dello stesso diagramma spaziale si comprende la
possibilità di permutazione degli assi, ottenendo diagrammi p - v con curve
parametriche in T, cioé isoterme, (diagramma di Clapeyron riportato in figura
7.4 e corrispondente alla proiezione di destra del diagramma di figura 7.2)
ovvero diagrammi T - v con parametro p (proiezione orizzontale del diagramma
tridimensionale).
Cap. 7
Pagina 9 di 25
vk = 0,00317 m3/kg
pk = 221,29 bar Tk = 374,15 °C
Figura 7.4 – Diagramma p,v con le curve parametriche isoterme (diagramma
di Clapeyron) per l’acqua ed i valori dei parametri critici.
Cap. 7
Pagina 10 di 25
Figura 7.5 – Diagramma Gibbs per l’acqua.
In tali diagrammi i cambiamenti di stato iniziano e terminano in precise
condizioni rappresentate da punti posti su curve chiamate curve di saturazione.
Si avranno così la curva di solido saturo, quella di liquido saturo per
incipiente solidificazione e di liquido saturo per incipiente evaporazione, quella
di vapore saturo prossimo alla condensazione e di vapore saturo prossimo alla
solidificazione.
Cap. 7
Pagina 11 di 25
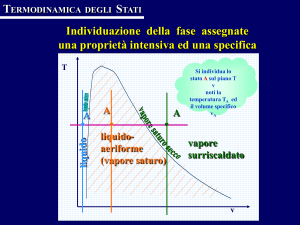
Nelle figure precedenti è riportata la terminologia corrente con cui si
indicano le varie condizioni della sostanza (solido, solido saturo, liquido,
liquido saturo, vapore saturo umido, vapore saturo secco, vapore surriscaldato,
gas).
Altri diagrammi di stato
Una qualsiasi terna di variabili di stato può essere correlata da una funzione
di stato, cui corrisponde una rappresentazione parametrica chiamata
diagramma di stato (in appendice è riportata una tabella con le definizioni
delle diverse funzioni di stato).
Fra i diagrammi parametrici possibili, oltre al diagramma di Clapeyron, si
evidenzia, per alcune utili proprietà, quello che sul piano s - T riporta
parametricamente la p (diagramma di Gibbs riportato in figura 7.5):
f T , s , p=0 .
Da ultimo l’entalpia:
f h , s , p=0
da cui il diagramma h - s con curve parametriche in p (diagramma di Mollier).
A volte su uno stesso diagramma (ad esempio il precedente diagramma di
Mollier), sul piano h - s, oltre alla curve parametriche isobare p, possono essere
indicate, magari in altro colore o con altro tratteggio, le curve isocore v,
quelle a titolo costante x, ed altre ancora.
Cap. 7
Pagina 12 di 25
Figura 7.6 – Diagramma Mollier per l’acqua.
Cap. 7
Pagina 13 di 25
Un diagramma molto utilizzato nel calcolo degli impianti frigorigeni è il
diagramma che riporta sul piano log p - h, le curve isobare, isoterme,
isentropiche ed a titolo costante (vedi figura 7.7).
Fgura 7.7 – Diagramma log p - h per l’ammoniaca.
Cap. 7
Pagina 14 di 25
Le anzidette relazioni, fra le varie grandezze di stato e specifiche, possono
essere fornite, oltre che da diagrammi, anche da espressioni analitiche, dette
equazioni di stato che approssimano l’andamento reale per le varie sostanze,
rilevato con metodi sperimentali. La complicazioni di tali espressioni dipende
dal comportamento, più o meno regolare, della sostanza trattata e dalla
precisione richiesta.
In alternativa ai diagrammi o alle equazioni di stato, possono essere fornite
delle tabelle di stato; esse sono costituite da una parte nella quale sono riportati
i valori di saturazione ed un'altra di valori generici nella quale, per una coppia
di grandezze, vengono forniti i valori di moltre altre (vedi tabelle in appendice,
sempre per l’acqua).
Sia sui diagrammi che nelle tabelle sono necessari calcoli di interpolazione,
molte volte non lineari, per la valutazione delle grandezze al di fuori delle curve
parametriche, nel caso di diagrammi, o dei valori tabulati.
Equazioni di stato generalizzate
L'uso sempre più diffuso dei calcolatori numerici ha spinto a cercare delle
espressioni analitiche che sostituiscano tabelle e diagrammi: una delle prime
equazioni è stata quella di Van der Waals cui ne sono seguite altre sempre più
complesse, fra cui la più consistente in dimensione risulta quella dell'acqua da
liquido a gas (l'acqua presenta un comportamento polare molto anomalo rispetto
alle sostanze simili).
Per calcoli con le precisioni ingegneristiche sono reperibili programmi che,
utilizzando tali formule, permettono di calcolare le varie grandezze
termodinamiche oltre che calcolare cicli e disegnare i diagrammi di stato.
Funzioni di stato ed energia utilizzabile (exergia)
Fra le precedenti funzioni di stato non è stata citata l’energia utilizzabile
(exergia); essa infatti presenta un valore definito in ogni stato termodinamico,
pur di aver stabilito il valore della temperatura ambiente di riferimento.
Cap. 7
Pagina 15 di 25
Pertanto, o si indica un valore convenzionale della temperatura ambiente,
oppure i diagrammi, le equazioni di stato e le tabelle, acquistano una variabile
in più, con grosse difficoltà di presentazione.
L’exergia però può essere derivata, con le espressioni fornite al Capitolo
quinto, dalle altre funzioni di stato disponibili (entalpia, entropia, calore interno,
ecc...).
Si fà notare che il diagramma di Mollier del vapore d'acqua contiene tutti gli
elementi per il calcolo dell’exergia per ogni stato termodinamico in esso
rappresentato, essendo:
b=h−h o−T o s−s0 ,
dove i simboli indicano:
b l’energia utilizzabile in J/kg,
h l’entalpia in Jt/kg,
T a la temperatura ambiente in K ,
s l’entropia specifica in Jt /kg °C .
Il pedice o indica la condizione di riferimento (generalmente 1 bar e 0 °C ad
eccezione dei fluidi refrigeranti o dei gas criogenici per i quali si usano altri
stati termodinamici).
Nella figura 7.8 è riportato il diagramma di Mollier con le curve isoexergia.
Cap. 7
Pagina 16 di 25
Figura 7.8 – Diagramma di Mollier per l’acqua con indicate le curve
isoexergia: il riferimento per la temperatura ambiente è 20°C.
Cambiamenti di stato e condizioni di saturazione
La situazione che la sostanza sta subendo un cambiamento di stato,
costituisce una condizione alternativa al valore di una variabile di stato; in altre
parole, mentre lo stato termodinamico di una sostanza pura è perfettamente
Cap. 7
Pagina 17 di 25
definito dalla conoscenza di due variabili indipendenti fra loro, in occasione del
cambiamento di stato, è sufficiente una sola grandezza, essendo il cambiamento
di stato, la seconda condizione.
Deriva di conseguenza che per ogni cambiamento di stato, fissata una
grandezza di stato, tutte le altre sono stabilite (e quindi non sono indipendenti
fra loro e con la prima scelta).
I valori delle variabili di stato sature si derivano dai diagrammi di stato o
dalle tabelle di saturazione corrispondenti alla sostanza desiderata.
Proprietà termodinamiche nella zona gas
Lo stato termodinamico di un gas (vedi anche tabelle in appendice) è
definito, come in qualsiasi campo, da due variabili, es. la pressione ed il volume
specifico.
L’equazione di stato, secondo il tipo di approssimazione scelta ed il campo
di pressione e di volume specifico, può essere:
a) gas ideale
per la temperatura:
T=
pv
R
per l’entalpia:
h=c p t−t o
Cap. 7
Pagina 18 di 25
per il calore interno:
u=c v t−t o
per l’entropia:
s=c p⋅log
T
p
T
v
−R log =c v⋅log R log
To
po
To
vo
Nelle relazioni precedenti i simboli hanno il seguente significato:
T temperatura assoluta in K,
T o temperatura assoluta di riferimento in K,
p
pressione assoluta in N/m2,
v
volume specifico in m3/kg,
R costante di elasticità del gas in K/m2s2,
h
entalpia specifica in Jt/kg,
c p calore specifico a pressione costante in Jt/kg C,
t
temperatura in °C,
to
temperatura di riferimento in °C (generalmente 0 °C),
u
calore massico interno (energia interna) in Jt/kg,
cv
calore specifico volume costante in Jt/kg C,
s
entropia specifica in Jt/kg C,
c
generico calore specifico Jt/kg °C,
log logaritmo naturale
Cap. 7
Pagina 19 di 25
b) gas reale
Il gas reale viene normalmente considerato come ideale ma con correzioni, di
derivazione sperimentale, valide per una specifica sostanza ed entro un limitato
campo di temperature e pressioni. Molte volte i termini correttivi vengono
forniti da diagrammi ovvero hanno un aspetto polinomiale.
Dati numerici specifici vengono forniti da libri specialistici.
Proprietà termodinamiche
surriscaldato
nella
zona
vapore
Valgono in prima approssimazione relazioni simili a quelle proposte per i
gas reali (al limite ideali per vapori molto rarefatti), ovviamente solo al di sopra
delle condizioni di saturazione.
In condizioni di metastabilità (cioé di precaria stabilità ottenuta con
particolari cautele) tali relazioni possono essere estese in una piccola fascia
vicina alla zona di saturazione.
Proprietà termodinamiche nella zona di vapore saturo
secco
I valori delle variabili di stato dipendono dal tipo di sostanza; essi sono
forniti da diagrammi o da apposite tabelle.
Cap. 7
Pagina 20 di 25
Proprietà termodinamiche nella zona di vapore umido
Il vapore umido può essere considerato come una miscela fra liquido saturo e
vapore saturo secco; pertanto viene definito il titolo del vapore x come
rapporto fra la massa di vapore saturo secco e la massa totale della miscela:
x=
mv
,
mv ml
con mv massa di vapore e ml massa di liquido.
Di conseguenza:
v=x v v 1−x v l
h=x h v 1− x hl
s=x s v 1− x sl
con:
v volume specifico
h entalpia specifica
s entropia specifica.
Gli indici v ed l corrispondono a vapore saturo secco e a liquido saturo.
Cap. 7
Pagina 21 di 25
Proprietà termodinamiche nella zona di liquido saturo
Si ritrovano su diagrammi e su tabelle, queste ultime generalmente associate
a quelle di vapore saturo secco.
Proprietà termodinamiche nella zona di liquido
Il volume specifico v viene calcolato tramite un volume di riferimento ed un
coefficiente di variazione con la temperatura:
v=v ol t−t o
con:
l coefficiente di dilatazione cubica, a volte considerato costante ed a
volte, come per l’acqua che presenta un comportamento anomalo, fornito da
diagrammi o tabelle,
v o volume specifico alla temperatura to di riferimento.
Il volume specifico varia pochissimo con la pressione e pertanto tali
variazioni sono considerate solo nel caso di pressioni molto elevate.
Per le altre grandezze valgono le relazioni:
h=hoc l t−t o
s=s oc l log
Cap. 7
T
To
Pagina 22 di 25
con:
c l calore specifico del liquido praticamente indistinto fra a pressione
costante ed a volume costante date le piccolissime variazioni di volume,
L'indice o corrisponde alla condizione di riferimento.
Proprietà termodinamiche nella zona di liquido-solido
Sono simili a quelle nella zona liquido-vapore (vapore saturo umido) e
pertanto definendo come titolo di liquido x x come rapporto fra la massa di
liquido e la massa totale della miscela liquido solido:
x x=
ml
,
ml m s
con ml massa di liquido e m s massa di solido.
Di conseguenza:
v=x x v l 1−x x v s
h=x x hl 1−x x h s
s=x x s l 1−x x s s
con:
v volume specifico
h entalpia specifica
Cap. 7
Pagina 23 di 25
s entropia specifica.
Gli indici l ed s corrispondono a liquido e solido saturi.
Proprietà termodinamiche nella zona di solido
Sono simili a quelle nella zona di liquido.
Il volume specifico v viene calcolato tramite un volume di riferimento ed un
coefficiente di variazione con la temperatura:
v=v ol t−t o
con:
l coefficiente di dilatazione cubica,
v o volume specifico alla temperatura t o di riferimento.
Anche per i solidi il volume specifico varia pochissimo con la pressione e
pertanto tali variazioni sono considerate solo nel caso di pressioni molto
elevate.
Per le altre grandezze valgono le relazioni:
h=hoc s t−t o
s=s oc s log
T
To
con:
Cap. 7
Pagina 24 di 25
cs
calore specifico del solido
generica e di riferimento.
T
e
To
le temperature assolute
Per i solidi si considera anche un coefficiente di dilatazione lineare che
risulta pari ad 1/3 del coefficiente di dilatazione cubica.
Cap. 7
Pagina 25 di 25