CAPITOLO
0
Alia debitat hictiun deliquiat la nonet liquatus anis atendam ideliquatur maximol
oressinctat od magnis sendantibea volupta commolu ptatur alia id ut aut repero
tempore icius, inctium fuga.
Et que nonseque reperibus, cuptatemqui comnihi liquunte providu?
SUWIT NGAOKAEW/Shutterstock
RICHIAMI suI MotI e le foRze
1
PosIzIone e dIstAnzA su unA RettA
Ricordiamo alcuni termini di base.
■
■
■
■
Punto materiale. Quando un oggetto è molto più piccolo dell’ambiente in cui si trova,
viene considerato come un punto materiale, cioè un punto senza dimensioni ma dotato
di massa.
Traiettoria. È la linea che congiunge tutti i punti dello spazio occupati da un punto materiale al trascorrere del tempo. Nel moto rettilineo la traiettoria è un segmento di retta.
Sistema di riferimento. Su una retta si definisce un sistema di riferimento scegliendo in
modo opportuno un punto origine e un verso positivo. In tal modo possiamo conoscere
la coordinata (o ascissa) di ogni punto sulla retta.
Posizione su una retta. Si chiama posizione s di un punto su una retta la coordinata di
tale punto.
Inoltre:
la distanza Ds tra due punti su una retta
è data dalla differenza tra le posizioni dei
due punti: Ds = s 2 - s1 .
distanza
percorsa
O
A
posizione s1
B
s
posizione s2
La distanza è positiva se il corpo si muove nel verso scelto come positivo sulla retta. È
negativa se si muove nel verso opposto.
eseMPIo
Un punto materiale passa dalla posizione s1 = 3,8 m alla posizione s2 = 7,1 m.
▶ Quanto vale la distanza Ds percorsa?
Direttamente dalla formula precedente otteniamo
Ds = s 2 - s1 = 7, 1 m - 3, 8 m = 3, 3 m .
4
RICHIAMI suI MotI e le foRze
2
0
IstAnte e InteRvAllo dI teMPo
Il valore che si legge sul display di un cronometro o sul quadrante di un orologio è detto
in fisica istante di tempo. Questo concetto permette di introdurre una seconda grandezza, l’intervallo di tempo:
l’intervallo di tempo Dt , o durata di un fenomeno, è dato dalla differenza tra l’istante finale t2 e l’istante iniziale t1:
Dt = t 2 - t1 .
Esattamente come un punto su una retta ha spessore nullo ed è indicato dalla sua posizione, così la durata di un dato istante di tempo è pari a 0 s.
eseMPIo
Al martedì la lezione di tennis inizia alle ore 17:20 e finisce alle ore 18:10.
▶ Quanto dura la lezione di tennis del martedì? L’orario 17:20 signifca 17 h 20
min, mentre l’orario 18:10 equivale a 18 h 10 min. Quindi la durata della lezione è
Dt =(18 h 10 min) − (17 h 20 min) = 50 min.
3
lA veloCItà
RICoRdA
La velocità media è definita come il rapporto tra la distanza percorsa e l’intervallo
di tempo impiegato:
v=
s -s
Ds
= t 2 - t1 .
Dt
2
1
[1]
Se ∆t è un intervallo di tempo finito, la formula precedente definisce la velocità media
vm; se ∆t tende a diventare piccolissimo, la stessa formula fornisce la velocità istantanea
v a un istante t fissato.
Nel Sistema Internazionale l’unità di misura della velocità è il metro al secondo (m/s);
spesso però le velocità sono misurate in kilometri all’ora (km/h).
segno di v
Dalla definizione, v ha sempre il segno di ∆s. Queste grandezze sono:
■
■
entrambe positive quando il moto avviene nel
verso scelto come positivo sulla retta;
entrambe negative quando il moto avviene
nel verso opposto a quello scelto come positivo sulla retta.
O
A
Δs > 0
v>0
Δs < 0
v<0
B
• Per passare dal valore
della velocità in km/h a
quello in m/s si divide
il valore numerico per
3,6:
km
10 3 m
=
90 h = 90
3, 6 # 10 3 s
90 m
m
= 3, 6 s = 25 s .
• Per passare dal valore
della velocità in m/s a
quello in km/h si moltiplica il valore numerico
per 3,6:
m
15 s =
km
= (15 # 3, 6) h =
km
= 54 h .
s
5
0
RICHIAMI suI MotI e le foRze
eseMPIo
Correndo lungo il corridoio, il gatto ha percorso 4,2 m in 1,1 s.
▶ Qual era la velocità media del gatto?
Dalla definizione precedente la velocità media del gatto si calcola come
vm =
4, 2 m
Ds
m
= 1, 1 s = 3, 8 s .
Dt
eseMPIo
In autostrada ho percorso 190 km in 1,58 h.
▶ Qual è stata la mia velocità media?
La velocità media vm si trova come
vm =
190 km
km
Ds
= 1, 58 h = 120 h .
Dt
eseMPIo
Considera il risultato dell’esercizio precedente.
▶ Quanto vale la stessa velocità, espressa in metri al secondo?
Per passare da km/h a m/s si divide per 3,6:
m
120 km h
km
120 km
s = 33, 3 m .
120 h =
= 3, 6 h $ km
s
km h
3, 6
h
m s
GRAfICI sPAzIo-teMPo e veloCItà-teMPo
Il cronotachigrafo presente su molti
mezzi pesanti disegna un grafico velocità-tempo: il particolare della figura a lato
mostra una scala orizzontale (su un arco
di circonferenza) che indica il tempo in
ore.
Un pennino disegna in corrispondenza
dei vari orari il grafico della velocità in
kilometri all’ora.
I grafici spazio-tempo
Un grafico spazio-tempo ha sull’asse orizzontale (delle ascisse) l’istante di tempo t e
sull’asse verticale (delle ordinate) la posizione s di un oggetto in movimento, modellizzato come punto materiale. In questo modo
6
Pavel Polkovnikov/Shutterstock
4
RICHIAMI suI MotI e le foRze
0
il grafico spazio-tempo permette di stabilire dove si trova un corpo in movimento a
un determinato istante di tempo.
Per esempio, il grafico a lato rappresenta un
punto materiale che:
posizione s (m)
■
6
5
4
all’istante t0 = 0 s si trova nella posizione
3
s0 = 2 m;
2
poi si allontana dall’origine arrivando alla
1
posizione s1 = 6 m all’istante t1 = 4 s;
dopo l’oggetto torna indietro, arrivando
O
1 2 3 4 5 6 7 8 9
istante di tempo t (s)
nell’origine delle posizioni (s2 = 0 m) all’istante t2 = 7 s;
infine inverte di nuovo il verso del moto, giunge in s3 = 5 m quando il cronometro segna
l’istante t3 = 9 s.
■
■
■
Dal grafico spazio-tempo si ricavano anche informazioni sulla velocità del corpo in movimento. Consideriamo infatti un grafico s-t (che descrive il moto di un oggetto) e due
suoi punti A e B:
■
la pendenza (coefficiente angolare)
della retta secante al grafico s-t nei due
punti dà il valore della velocità media
dell’oggetto nell’intervallo di tempo
considerato. Nell’esempio qui sotto,
l’intervallo di tempo è tra tA = 1 s e
tB = 5 s.
■
La velocità istantanea dell’oggetto è
data dalla pendenza della retta tangente al grafico s-t in un suo punto. Nell’esempio qui sotto si può calcolare la velocità media all’istante tB = 5 s, quando
l’oggetto occupa la posizione sB = 3 m.
posizione s (m)
posizione s (m)
6
6
5
5
4
4
B
3
2
2
A
1
1
Ð1
O
B
3
1
2
3
4
5
6
7
Ð1
O
1
2
3
4
5
6
7
istante di tempo t (s)
eseMPIo
Un pedone passeggia nervosamente avanti
e indietro sul marciapiede. Partendo dal
centro di una porta che si apre sul marciapiede, il grafico spazio-tempo della persona
è quello riportato a lato.
▶ Descrivi schematicamente il movimento
della persona sul marciapiede.
7
0
RICHIAMI suI MotI e le foRze
·
·
·
·
·
·
·
·
All’istante iniziale (t0 = 0 s, quando iniziamo l’osservazione) il pedone si trova
nel punto di riferimento (il centro della porta) che facciamo corrispondere all’origine del sistema di riferimento;
poi comincia ad allontanarsi da esso fino a raggiungere un punto 6 m più distante;
torna indietro fino a trovarsi a 2 m dal punto di partenza;
si volta di nuovo e si allontana fino a trovarsi a 8 m dal punto di riferimento;
infine torna di nuovo sui suoi passi, oltrepassa l’origine e si ferma un metro
dopo.
I punti C e D del grafico hanno coordinate C(8 s, 2 m) e D(14 s, 8 m);
tra di essi si calcolano un intervallo di tempo Dt = (14 - 8) s = 6 s e una distanza Ds = (8 - 2) m = 6 m ;
quindi la velocità media in quel tratto risulta
v=
Ds
6m
m
= 6s = 1 s .
Dt
I grafici velocità-tempo
Un grafico velocità-tempo ha sull’asse orizzontale (delle ascisse) l’istante di tempo t e
sull’asse verticale (delle ordinate) la velocità istantanea v di un oggetto in movimento,
modellizzato come punto materiale. In questo modo
il grafico velocità-tempo permette di stabilire quanto vale la velocità di un corpo a
un determinato istante di tempo.
Per esempio, il grafico a lato mostra la velocità
di un oggetto (modellizzato come punto materiale) che:
all’istante t0 = 0 s possiede una velocità
v0 = 3 m/s e che aumenta la propria velocità
fino a raggiungere il valore v1 = 5 m/s all’istante t1 = 6 s;
poi mantiene costante la velocità per 2 s (fino
all’istante t2 = 8 s);
in seguito diminuisce la velocità fino a raggiungere il valore di 2 m/s all’istante finale (in
cui smettiamo di studiare il moto) t3 = 11 s.
■
■
5
B
5
velocità v (m/s)
■
6
C
4
A
3
D
2
1
O
2
4
6
8
10
istante di tempo t (s)
12
Il Moto RettIlIneo unIfoRMe
Si chiama moto rettilineo uniforme il movimento di un punto materiale che percorre una traiettoria rettilinea con velocità costante.
8
RICHIAMI suI MotI e le foRze
0
Ciò significa che:
■
■
■
la velocità media è la stessa su qualunque intervallo di tempo o su qualunque distanza
la si calcoli;
la velocità istantanea in ogni punto e in ogni momento risulta sempre la stessa ed è
uguale alla velocità media;
le distanze percorse risultano direttamente proporzionali agli intervalli di tempo impiegati.
la legge del moto
La legge del moto rettilineo uniforme fornisce la posizione s del punto materiale se si
conoscono il corrispondente istante di tempo t, la velocità v con cui il corpo si muove e
la sua posizione iniziale s0:
s = s 0 + vt.
[2]
Formule inverse:
v=
s - s0
t
s
av = t k;
t=
s - s0
v
s
at = v k .
Le formule tra parentesi valgono nel caso semplice in cui si pone s0 = 0.
Il grafico spazio-tempo del moto rettilineo uniforme
Il grafico spazio-tempo del moto rettilineo uniforme è una retta.
■ Come mostra la figura, quando si ha
s0 = 0 m la retta passa per l’origine degli assi coordinati.
■ La retta è crescente quando la velocità è positiva, decrescente quando la
velocità del moto è negativa.
posizione s (m)
posizione s (m)
v>0
s0 ⫽ 0
s0 ⫽ 0
O
istante di tempo t (s)
v<0
O
istante di tempo t (s)
eseMPIo
Un ciclista partecipa a una gara a cronometro. Arrivato a 21,3 km dalla partenza, il
ciclista mantiene una velocità costante di 12,9 m/s per 15,8 minuti.
▶ In che posizione si trova alla fne di questo intervallo di tempo?
s
k = 948 s .
· Il tempo di 15,8 minuti corrisponde a (15, 8 min) # a60 min
9
0
RICHIAMI suI MotI e le foRze
·
Allora la posizione finale s del ciclista risulta
mk
s = s 0 + vt = 2, 13 # 10 4 m + a12, 9 Y
s) =
s # (948 Y
= 2, 13 # 10 4 m + 1, 22 # 10 4 m = 3, 35 # 10 4 m .
Cioè, il ciclista si trova a 33,5 km dalla partenza.
eseMPIo
In una gara di staffetta il quarto corridore della squadra A riceve il testimone per
correre gli ultimi 85 m. Nello stesso istante l’ultimo atleta della squadra B si trova
in svantaggio di 2,6 m.
L’atleta della squadra A corre alla velocità di 9,45 m/s, mentre quello della squadra
B riesce a correre alla velocità di 9,80 m/s.
▶ L’ultimo stafettista della squadra B riesce a vincere la gara?
·
Scegliamo come origine delle posizioni il punto da cui parte l’atleta della squadra
A. Così il corridore della squadra B ha una posizione iniziale s0 = −2,6 m.
· La legge della posizione dell’atleta A è s A = a9, 45 ms kt .
· La legge della posizione dell’atleta B è s B = a9, 80 ms kt - 2, 6 m.
· L’atleta B raggiunge (e sorpassa) il corridore A quando i due staffettisti occupano la stessa posizione: sB = sA.
· Dalla condizione precedente si ottiene
m
m
m
m
a9, 80 s k t - 2, 6 m = a9, 45 s k t & a9, 80 s k t - a9, 45 s k t = 2, 6 m
2, 6 m
m
& a0, 35 s k t = 2, 6 m & t =
m = 7, 4 s.
0, 35 s
All’istante t = 7,4 s il corridore A si trova nella posizione
m
s A = a9, 45 s k# ^7, 4 sh = 70 m.
Dal momento che 70 m è minore della lunghezza (pari a 85 m) dell’ultimo tratto di
gara, il corridore della squadra B riesce a superare l’atleta della squadra A.
6
l’ACCeleRAzIone
L’accelerazione è definita come il rapporto tra la variazione di velocità di un punto materiale e l’intervallo di tempo impiegato a realizzare tale variazione di velocità:
a=
v -v
Dv
= t2 - t 1 .
Dt
2
1
[3]
Se ∆t è un intervallo di tempo finito, la formula precedente definisce l’accelerazione
media am; se ∆t tende a diventare piccolissimo, la stessa formula fornisce l’accelerazione
istantanea a in corrispondenza di un istante t fissato.
Nel Sistema Internazionale l’unità di misura dell’accelerazione è il metro al secondo
quadrato (m/s2). Una accelerazione di 1 m/s2 indica che in ogni secondo la velocità sta
aumentando 1 m/s.
10
RICHIAMI suI MotI e le foRze
0
Il segno dell’accelerazione
Un’accelerazione:
■
■
positiva indica che si ha Dv 2 0 , cioè che la velocità sta aumentando;
negativa indica che si ha Dv 1 0 , cioè che la velocità sta diminuendo.
Bisogna fare attenzione:
■
a > 0 non significa sempre che il corpo «va più forte». Per esempio, consideriamo
una bicicletta che sta tornando indietro sulla retta orientata, e quindi ha velocità di
segno negativo: se nell’intervallo di tempo ∆t = 1 s la sua velocità passa da v1 = −5 m/s
a v2 = −3 m/s, la sua accelerazione media vale
m
m
m
a- 3 s k - a- 5 s k
2 s
v 2 - v1
m
=
= 1 s = 2 2 2 0.
a=
1s
s
Dt
L’accelerazione è positiva perché il valore della velocità aumenta, da −5 m/s a
−3 m/s. Però il tachimetro della bicicletta prima indicava 18 km/h e dopo indica circa
11 km/h, quindi la bicicletta dopo un’accelerazione positiva «va più piano»;
a < 0 non significa sempre che il corpo sta decelerando: basta pensare al caso precedente, con la bicicletta che passa da −3 m/s a −5 m/s.
Dal grafico velocità-tempo si ricavano informazioni sull’accelerazione del corpo in movimento. Consideriamo infatti un grafico v-t come
quello a lato e due suoi punti A e B: la pendenza
della retta secante al grafico nei due punti considerati fornisce l’accelerazione media del moto
nell’intervallo di tempo corrispondente.
4
velocità v (m/s)
■
B
3
A
2
1
O
1
2 3 4 5 6 7
istante di tempo t (s)
8
eseMPIo
In 25 s un’automobile passa dalla velocità iniziale di 85 km/h alla velocità finale di
121 km/h.
▶ Calcola l’accelerazione media dell’automobile.
La variazione di velocità dell’automobile è
km
km
1 m/s
m
Dv = (121 - 85) h = 36 h # 3, 6 km/h = 10 s .
Quindi l’accelerazione media risulta
m
10 s
Dv
m 1
m
a=
= 25 s = 0, 40 s $ s = 0, 40 2 .
s
Dt
eseMPIo
Un ciclista viaggia su una strada rettilinea alla velocità vi = 12,4 m/s. A un certo
punto agisce sui freni per 0,40 s ottenendo un’accelerazione costante di −5,7 m/s2.
▶ Qual è la velocità del ciclista alla fne della frenata?
Dv
a=
Dalla definizione
Dt
11
0
RICHIAMI suI MotI e le foRze
otteniamo
m
m
k # (0, 40 s) =- 2, 3 s ,
s2
per cui la velocità finale vf del ciclista è
Dv = a Dt = a- 5, 7
m
m
m
v f = vi + Dv = 12, 4 s + a- 2, 3 s k = 10, 1 s .
eseMPIo
È dato il grafico velocità-tempo della figura a lato.
▶ Determina l’accelerazione media del
moto nel tratto compreso tra tA = 2 s
e tB = 10 s.
·
·
·
7
Gli istanti di tempo citati nel testo
dell’esercizio si riferiscono ai punti A
e B della figura, che hanno coordinate
A(2 s, 3 m/s) e B(10 s, 1 m/s).
Relativamente a essi si possono quindi calcolare l’intervallo di tempo
Dt = (10 - 2) s = 8 s e la variazione di
velocità Dv = (1 - 3) m/s =- 2 m/s .
Di conseguenza l’accelerazione media risulta
m
Dv
- 2 m/s
= 8 s =- 0,25 2 .
a=
s
Dt
Il Moto RettIlIneo unIfoRMeMente
ACCeleRAto
Si chiama moto rettilineo uniformemente accelerato il movimento di un punto
materiale che percorre una traiettoria rettilinea con accelerazione costante.
Ciò significa che:
■
■
■
l’accelerazione media è la stessa su qualunque intervallo di tempo e su qualunque distanza la si calcoli;
l’accelerazione istantanea in ogni punto e in ogni momento risulta sempre la stessa e
uguale all’accelerazione media;
le variazioni di velocità del corpo risultano direttamente proporzionali agli intervalli di
tempo impiegati.
Un corpo lasciato cadere, oppure lanciato in verticale in prossimità della superficie terrestre descrive un moto uniformemente accelerato con un’accelerazione che in valore
assoluto vale circa g = 9,8 m/s2.
la legge della velocità nel moto rettilineo uniformemente
accelerato
La legge della velocità fornisce la velocità v del punto materiale se si conoscono il corri-
12
RICHIAMI suI MotI e le foRze
0
spondente istante di tempo t, l’accelerazione a con cui il corpo si muove e la sua velocità
iniziale v0:
v = v0 + at.
[4]
Formule inverse:
a=
v - v0
t
v
aa = t k;
t=
v - v0
a
v
at = a k .
Le formule tra parentesi valgono nel caso semplice del moto con partenza da fermo, per
cui si ha v0 = 0.
la legge della posizione nel moto rettilineo uniformemente
accelerato
La legge della posizione permette di calcolare la posizione s del punto materiale se si
conoscono la sua accelerazione a, l’istante di tempo t, la sua velocità iniziale v0 e la posizione iniziale s0:
1
s = s 0 + v0 t + 2 at 2
[5]
Formule inverse:
a=
- v0 !
2 (s - s 0) - 2v 0 t
2s
a = 2 l; t =
b
2
t
t
v 20 + 2a ^s - s 0h
bt =
a
2s
a l.
Le formule tra parentesi valgono per un moto che parte da fermo nell’origine del sistema di riferimento (v0 = 0 e s0 = 0).
Grafici spazio-tempo e velocità-tempo nel moto
uniformemente accelerato
Il grafico spazio-tempo del moto rettilineo uniformemente accelerato è una parabola.
■ Se il corpo parte da fermo, il vertice
della parabola è sull’asse delle ordinate.
In particolare, è nell’origine se vale anche s0 = 0.
■ Se a è positiva, la concavità della parabola è verso l’alto; altrimenti (come
nella figura precedente) la concavità è
verso il basso.
posizione s (m)
posizione s (m)
v0 = 0
a<0
v0 Þ 0
a>0
velocità v (m/s)
v0 Þ 0;a > 0
O
istante di tempo t (s)
O
istante di tempo t (s)
Nel moto uniformemente accelerato il grafico velocità-tempo è una retta. Essa passa per
l’origine se v0 = 0, è crescente se a è positiva ed è decrescente se a è negativa.
O
v0 = 0;a < 0
istante di tempo t (s)
13
0
RICHIAMI suI MotI e le foRze
eseMPIo
Una palla da tennis è lasciata cadere (da ferma) da un’altezza di 2,0 m.
▶ Quanto tempo impiega a cadere?
▶ Con che velocità arriva a terra?
·
In questo caso poiché la velocità di caduta e l’accelerazione sono rivolte entrambe verso il basso possiamo orientare l’asse del moto verso il basso.
La caduta finisce all’istante
2 # (2, 0 m)
= 0, 64 s .
m
9, 8 2
s
Poiché v0 = 0 m/s, la velocità v alla fine della caduta vale
m
m
v = gt = a9, 8 2 k # ^0, 64 sh = 6, 3 s .
s
t=
·
2s
a =
2s
g =
eseMPIo
Un sasso viene lanciato verso l’alto con una velocità iniziale di 9,3 m/s.
▶ Calcola quanto dura il moto di salita del sasso.
▶ Trova l’altezza massima raggiunta dal sasso, rispetto al punto da cui è partito.
·
RICoRdA
Con la nostra scelta
del sistema di riferimento il segno della
velocità è positivo
mentre il sasso sale
ed è negativo mentre
esso scende. Nel
punto più alto la velocità è nulla perché
passa da positiva a
negativa. Nel punto
di massima quota il
sasso è «istantaneamente fermo».
·
·
·
Orientiamo verso l’alto il sistema di riferimento per la velocità. In questa situazione l’accelerazione del sasso ne diminuisce la velocità, per cui risulta di segno
negativo: a = −g.
1
Quindi scriviamo le leggi del moto come v = v0 - gt e s = v0 t - 2 gt 2 .
Nel punto più alto del moto la velocità istantanea è v = 0 m/s. Dalla prima delle
equazioni precedenti si trova, quindi:
m
9, 3 s
v0
0 = v 0 - gt & t = g =
m = 0, 95 s .
9, 8 2
s
L’altezza massima del sasso si calcola con la seconda delle equazioni precedenti:
1
m
1
m
s = v 0 t - 2 gt 2 = a9, 3 s k # ^0, 95 sh - 2 # a9, 8 2 k # ^0, 95 sh2 =
s
= 8, 8 m - 4, 4 m = 4, 4 m.
8
GRAfICI sPAzIo-teMPo e veloCItà-teMPo
Rappresentiamo i moti studiati utilizzando dei grafici.
Moti uniformi e moto rettilineo uniforme; grafici spazio-tempo
■
Un punto materiale parte dall’origine e si muove a velocità costante fino
alla posizione s = 10 m. poi rimane fer-
14
■
Il corpo B è fermo per tutto il tempo
nella posizione s = 10 m. Il corpo A si
muove alla velocità costante di 0,5 m/s
RICHIAMI suI MotI e le foRze
mo per 4 s e infine torna indietro, in
maniera più rapida (da 10 s a 14 s) e
poi più lenta. In ognuno dei tratti la velocità è costante.
e raggiunge il corpo B all’istante
t = 20 s (ascissa del punto P), per poi
continuare il suo moto.
12
posizione s (m)
posizione s (m)
12
10
8
6
4
2
P
10
B
8
6
4
A
2
0
0
0 2 4 6 8 10 12 14 16 18 20 22
0 2 4 6 8 10 12 14 16 18 20 22
istante di tempo t (s)
istante di tempo t (s)
■ Due nuotatori partono insieme per i
50 m stile libero. A nuota alla velocità
costante di 2,0 m/s, B a 1,8 m/s; così A
arriva al traguardo dopo 25 s mentre B
ritarda di 2,8 s. Questo distacco è rappresentato dal segmento arancione
sull’asse t.
posizione s (m)
■ Un calciatore si riscalda lungo la linea laterale del campo. La posizione
s = 0 m indica la metà campo. Si sposta
dalla sua metà campo a quella degli avversari, ritorna dalla sua parte e poi si
ferma vicino alla linea di metà campo.
posizione s (m)
0
20
15
10
5
50
40
A
30
B
20
0
0
5
10
15
20
Ð5
25
30
35
40
45
10
istante di tempo t (s)
0
Ð10
0
5
10
15
20
25
30
istante di tempo t (s)
■
Il motorino A si muove alla velocità
di 12 m/s e parte dall’inizio della strada. Il motorino B parte invece 800 m
più avanti, ma la sua velocità è minore
(8,0 m/s). Così il motorino A sorpassa
B. Il sorpasso è rappresentato dal punto P di intersezione tra il grafico di A e
quello di B, all’istante t = 200 s e nella
posizione s = 2400 m.
■
Il motorino A percorre la strada a
velocità costante. Quando A parte
dall’inizio della strada, il B è a 3 km di
distanza e si muove nel verso opposto:
il suo grafico (in blu), è decrescente. I
due motorini si incrociano all’istante
t = 160 s e a 1800 m dall’inizio della
strada, come si capisce dalle coordinate del punto di intersezione P.
posizione s (m)
posizione s (m)
3000
3000
B
P
2400
2400
B
1800
A
1200
P
1800
A
1200
600
600
0
0
0
40
80
120
160
200
240
280
istante di tempo t (s)
0
40
80
120
160
200
240
280
istante di tempo t (s)
15
0
RICHIAMI suI MotI e le foRze
Moto rettilineo uniformemente accelerato; grafici spaziotempo e velocità-tempo
Una slitta scende lungo una pista ben preparata e liscia con una accelerazione costante
di 2 m/s2.
■
■
Il grafico velocità-tempo è una retta
passante per l’origine; a ogni secondo
che passa la velocità della slitta aumenta di 2 m/s. Ecco perché nello stesso
tempo di 1 s la slitta percorre distanze
sempre maggiori.
v (m/s)
posizione s (m)
Il grafico spazio-tempo è una parabola con il vertice nell’origine. I punti
rossi sull’asse s mostrano dove si trova
la slitta all’istante di tempo corrispondente. In ogni secondo la slitta percorre 2 m in più rispetto al secondo precedente.
16
12
8
6
8
4
4
2
0
0
0
0,5
1
1,5
2
2,5
3
3,5
4
0
5
4,5
0,5
1
1,5
2
2,5
3
3,5
4
istante di tempo t (s)
istante di tempo t (s)
Un motorino percorre una strada rettilinea alla velocità di 6 m/s. Quando si trova a 10
m dall’inizio della strada, il guidatore accelera per 5 s con un’accelerazione di 2 m/s2.
■
■
Il grafico velocità-tempo è una retta
che non passa per l’origine. Come nel
caso precedente, la retta è inclinata
verso l’alto. Quindi il valore della velocità aumenta al passare del tempo.
posizione s (m)
posizione s (m)
Il grafico spazio-tempo è una parabola con la concavità verso l’alto. Il
vertice non è nell’origine. Ancora una
volta, in ogni intervallo di tempo pari a
1 s il motorino percorre distanze sempre più grandi.
50
40
12
10
8
6
30
4
20
2
10
0
0
0
1
2
3
4
5
istante di tempo t (s)
0
1
2
3
4
istante di tempo t (s)
Una ragazza su uno skateboard affronta una rampa piana in salita. La sua velocità iniziale è 8 m/s e l’accelerazione del suo moto lungo la rampa è uguale a 4 m/s2.
16
RICHIAMI suI MotI e le foRze
■
0
■
Il valore della sua velocità diminuisce di 4 m/s durante ogni secondo:
all’inizio la velocità è positiva (verso
l’alto), poi si annulla e quindi diventa
negativa (verso il basso). Durante la salita il modulo di v diminuisce e lungo
la discesa aumenta.
velocità v (m/s)
posizione s (m)
La ragazza risale la rampa sempre
più lentamente, giunge al punto più
alto a 8 m dalla partenza e poi ridiscende la rampa in modo sempre più rapido. Le distanze percorse in 0,5 s si accorciano durante la salita e si allungano
nella discesa.
8
6
4
2
0
istante di tempo t (s)
0
0,5
1
1,5
2
2,5
3
3,5
4
–2
–4
–6
0
1
2
3
–8
4
istante di tempo t (s)
9
lA foRzA-Peso
Un corpo di massa m che si trova nelle vicinanze della superficie terrestre è soggetto a
una forza verso il basso chiamata forza-peso FP e descritta dalla formula
FP = mg.
[6]
Il vettore g si chiama «accelerazione di gravità» è diretto verso il centro della Terra e
il suo valore è lo stesso per tutti i corpi che si trovano nella stessa zona della superficie
terrestre, qualunque sia la loro forma, dimensione e composizione chimica. Nel Sistema
Internazionale g si misura in N/kg o in m/s2; le due unità di misura sono equivalenti.
Invece il valore g varia da punto a punto della superficie terrestre, passando da 9,78 m/s2
(attorno all’equatore) a 9,83 m/s2 (ai poli). Come si è visto in precedenza, nei calcoli si
utilizza un valore medio, pari a 9,8 m/s2.
In Italia, al livello del mare, il valore di g vale 9,80 m/s2 per latitudini all’incirca inferiori
a quella di Pisa e 9,81 m/s2 per quelle superiori.
eseMPIo
Il cane di un mio amico ha una massa m = 47 kg.
▶ Quanto vale il suo peso?
Il peso del cane è
N
FP = mg = (47 kg) # c 9, 8 kg m = 4, 6 # 10 2 N.
eseMPIo
Una trave poggia sulle pareti con un peso FP = 8,5 × 103 N.
▶ Calcola la massa della trave.
La massa m richiesta è
F
8, 5 # 10 3 N
= 8, 7 # 10 2 kg.
m = gP =
N
9, 8 kg
17
0
RICHIAMI suI MotI e le foRze
10
forza elastica Fe (N)
lA foRzA dI Hooke
Una molla deformata esercita una forza che ha la stessa direzione della deformazione e
verso opposto a essa. Il modulo di questa forza Fe , detta forza elastica o forza di Hooke,
è dato dalla formula
Fe = kx
Fe = kx
[7]
dove x è la lunghezza della deformazione e k è una costante di proporzionalità, detta
costante elastica, che dipende dalla molla. Quindi, come mostra anche il grafico,
O
deformazione x (m)
il valore della forza elastica esercitata da una molla è direttamente proporzionale
all’entità della deformazione che essa subisce.
La costante k:
■
■
è una grandezza che caratterizza la maggiore o minore rigidità della molla;
nel Sistema Internazionale, si misura in newton fratto metro (N/m).
Un piccolo valore di k corrisponde a una molla che si deforma facilmente perché si oppone a una deformazione con una forza poco intensa. Al contrario, un grande valore di
k descrive una molla piuttosto rigida che si oppone a una deformazione, anche piccola,
generando una forza intensa.
eseMPIo
Una molla di costante elastica k = 580 N/m è accorciata di 7,35 cm.
▶ Calcola la forza F necessaria per mantenere la molla in tale condizione.
La forza richiesta è uguale e opposta a quella esercitata dalla molla, per cui ha lo
stesso modulo. Quindi troviamo
N
F = Fe = kx = b580 m l # (0, 0735 m) = 42, 6 N.
11
lA foRzA dI AttRIto RAdente
Un corpo appoggiato su un piano o che striscia su di esso subisce una forza di attrito
radente.
forza di attrito radente statico
Se si cerca di spingere in orizzontale una valigia si avverte una forza di attrito che si oppone allo spostamento; questo è un esempio di attrito radente statico. Spingendo con
più forza si riesce a fare scivolare la valigia sul pavimento.
Fino a quando la forza F che esercitiamo sulla valigia è abbastanza piccola, l’attrito
riesce a esercitare sulla valigia stessa una forza di reazione uguale e opposta a F , per
cui la forza orizzontale totale che si esercita sulla valigia è nulla ed essa rimane ferma.
Quando la forza F diventa eccessiva, la forza di attrito radente non riesce a uguagliarne
il modulo e la valigia si muove.
18
RICHIAMI suI MotI e le foRze
0
La forza di attrito al distacco Fs, cioè la massima forza di attrito radente che si può esercitare tra i due oggetti appoggiati uno sull’altro, è data dalla formula
Fs = n s F=
[8]
dove F= è la forza premente e n s è un numero puro che descrive quanto è intensa l’interazione tra i due oggetti appoggiati l’uno sull’altro. Quindi la forza di attrito:
■
■
■
dipende dalle proprietà delle due superfici a contatto;
dal materiale da cui esse sono fatte;
non dipende dall’estensione delle superfici a contatto.
La forza premente F= è il modulo della forza, diretta perpendicolarmente al piano
di appoggio, che spinge verso di esso l’oggetto a contatto con esso.
Spesso la forza premente è uguale alla forza-peso del corpo appoggiato (se il piano di
appoggio è orizzontale) o al modulo del componente della forza-peso perpendicolare al
piano. Ma, come mostra la figura a lato, può avere valori molto diversi dal peso.
F⊥ ,2
F⊥ , 1
forza di attrito radente dinamico
La forza di attrito radente dinamico Fd si esercita tra un corpo che scivola e la superficie
su cui avviene il moto. Essa è data dalla relazione
Fd = nd F=
[11]
dove la forza premente F= è la stessa descritta nell’attrito radente statico.
Valgono le seguenti proprietà:
■
■
■
il coefficiente nd è in generale minore del valore di n s relativo alla stessa situazione
fisica;
come nel caso statico, Fd non dipende dall’area delle superfici a contatto;
inoltre Fd non dipende dalla loro velocità relativa.
eseMPIo
Un libro appoggiato sul tavolo ha una massa di 450 g; il coefficiente di attrito statico
tra il tavolo e il libro vale 0,14. Una persona, con la mano, spinge il libro in orizzontale con una forza che ha modulo F = 0,50 N.
▶ Il libro si muove sul tavolo?
·
·
Visto che il tavolo è orizzontale, la forza premente è uguale al peso FP del libro.
La forza di attrito al distacco tra il tavolo e il libro ha modulo
N
Fs = n s F= = n s mg = 0, 14 # (0, 450 kg) # c 9, 8 kg m = 0, 62 N.
·
0,62 N è maggiore di 0,50 N: quindi la forza di attrito statico tra il tavolo e il libro
riesce a compensare la forza applicata con la mano e il libro rimane fermo.
19
ESERCIZI
l’altro è di 3 m. Le signore si spostano solo con l’ascensore.
▶ Calcola la distanza percorsa con l’ascensore da ciascuna signora per salire sul terrazzo.
0
▶ Calcola la distanza percorsa da ognuna delle signore
per rientrare a casa propria.
RICHIAMI suI MotI e le foRze
[29 m; 23 m; 15 m; 9 m]
6
1
1
★★★
★★★
PosIzIone e dIstAnzA su unA
RettA
Una caramella cade sul marciapiede mobile di un aeroporto in un punto che dista 11,8 m dall’inizio del marciapiede stesso; poi la caramella viene raccolta quando si
trova a 19,6 m dall’inizio del marciapiede.
▶ Che distanza è stata percorsa dalla caramella sul marciapiede mobile?
■ 15,7 km prima del casello di Cesena, provenendo da
Forlì.
▶ Calcola la distanza che il camionista deve percorrere
per arrivare alla stazione di servizio.
[7,8 m]
2
★★★
▶ La distanza cambia a seconda del riferimento scelto?
A fanco di una pista di atletica sono segnate le distanze a
partire dalla linea di partenza. Un atleta passa dal punto
segnato come «54 m» fno al punto segnato come «22 m».
▶ Che distanza ha percorso l’atleta sulla pista?
? ? km
BO
4,8 km
[−32 m]
2
7
3
★★★
La distanza Bologna–Rimini Nord in autostrada
è 122,6 km. Un motociclista imbocca l’autostrada a Imola che dista da Bologna 45,3 km.
▶ Calcola quanti km deve percorrere il motociclista per
arrivare al casello di Rimini Nord.
▶ Calcola quanti km in più deve percorrere il motociclista, se per distrazione, è costretto a uscire al casello di
Rimini Sud che dista da Bologna 132,2 km.
★★★
4
La fermata dell’autobus che Roberto prende la mattina
per andare a scuola dista dalla sua casa 500 m e la distanza complessiva casa-scuola è di 4,1 km. La fermata a cui
scende Roberto è proprio davanti alla sua scuola.
A causa di lavori lungo il percorso, Roberto è costretto a
scendere prima e percorrere a piedi 800 m.
▶ Calcola la distanza percorsa con l’autobus nel percorso casa-scuola, in condizioni normali e quando ci sono
i lavori stradali in corso.
8
★★★
5
20
Le signore Rossi e Bianchi si incontrano sul terrazzo del
loro palazzo, posto a 32 m da terra, per stendere la biancheria. Scendono poi insieme e si fermano al sesto piano
dalla loro amica comune Verdi per un cafè. La signora
Rossi abita al primo piano, mentre la signora Bianchi abita
al terzo. Considera, in media, che la distanza tra un piano e
Faenza
64,5 km
Forlì
81,5 km
Cesena Rimini-Sud
99,7 km
127,4 km
IstAnte e InteRvAllo dI teMPo
Durante una gara sui cento metri Marta sorpassa Laura
quando il tabellone luminoso segna 4,2 s e poi sorpassa
Gaia quando sul tabellone si legge 7,3 s.
▶ Quanto tempo separa i due sorpassi?
Durante un esperimento controllato da un cronometro digitale una pallina che cade arriva a metà del percorso dell’istante t1 = 0,429 s e arriva in fondo all’istante t2 = 0,606 s.
▶ Quanto dura la caduta nella seconda metà del percorso?
[0,177 s]
9
★★★
Uno studente prende il treno alle 6:35 per andare a scuola e arriva alle 7:50.
▶ Calcola la durata del viaggio espressa in secondi.
[4,5× 103 s]
10
★★★
[3,6 × 103 m; 2,8 × 103 m]
★★★
50,1 km
[3,1 s]
[77,3 km; 9,6 km]
★★★
Imola
[2,4 km]
▶ Si è allontanato dalla linea di partenza o si è avvicinato a essa?
Un camionista, che si trova a Forlì, deve raggiungere una
stazione di servizio dove ha un appuntamento con un
collega.
Telefonando al servizio autostradale riceve le seguenti informazioni sulla posizione della stazione di servizio:
■ 2400 m dopo il casello di Forlì;
Una corsa ciclistica a cronometro è iniziata alle
9 h 30 min 10 s. Il primo ciclista taglia il traguardo alle
11 h 50 min 30 s, mentre il secondo alle 11 h 51 min 35 s.
▶ Calcola l’intervallo di tempo impiegato dal vincitore
della corsa e dal secondo classifcato.
▶ Calcola l’intervallo di tempo che separa i due ciclisti.
[2 h 20 min 20 s; 2 h 21 min 25 s; 1 min 05 s]
11
★★★
Luca mette in carica il telefono e il tablet alle 15 h 20 min 30 s.
ESERCIZI
RICHIAMI suI MotI e le foRze
Il telefono completa la carica alle 16 h 30 min 45 s, mentre
il tablet risulta completamente carico alle 17 h 05 min 55 s.
▶ Calcola l’intervallo di tempo necessario per ricaricare
la batteria del telefono e del tablet.
[1 h 10 min 15 s; 1 h 45 min 25 s]
12
★★★
cicletta, alla velocità di 18 km/h.
[6,0 km; 20 min]
17
★★★
Marco e la sua famiglia, per raggiungere la città di Ancona, viaggiano in treno da Bologna secondo la tabella
riportata. Al ritorno, decidono di prendere un treno più
veloce riducendo del 15% il tempo di viaggio.
Città
Matteo si sta allenando per le gare di nuoto in una piscina olimpionica di lunghezza 50 m. L’allenatore registra i
tempi di 40 s e 45 s rispettivamente all’andata e al ritorno.
▶ Calcola i moduli delle velocità medie di Matteo nel
percorrere la vasca all’andata e al ritorno.
▶ Calcola la velocità media dell’intero percorso, considerando il ritorno con il segno corretto.
▶ Calcola la velocità media dell’intero percorso come si
OrariO
Bologna
p.9:19
Rimini
a.10:14
p.10:16
Pesaro
a.10:33
p.10:35
Ancona
a.11:06
fa nello sport, cioè considerando il ritorno come una
prosecuzione dell’andata.
[1,3 m/s; 1,1 m/s; 0 m/s; 1,2 m/s]
18
★★★
▶ Calcola l’intervallo di tempo per ogni tappa e il tempo
complessivo del viaggio di andata.
▶ Calcola l’intervallo di tempo del viaggio di ritorno
e l’ora di arrivo a Bologna se Marco parte col treno
alle 17:30.
Dopo gli esami Andrea e Giovanni decidono di raggiungere, con la bicicletta, gli amici al mare a Capalbio, che
dista 122 km dal loro luogo di partenza. Il loro programma prevede di mantenere una velocità di 18 km/h.
▶ Calcola quanti km percorrono nelle prime 3,0 h di
viaggio.
▶ Calcola quanto tempo servirebbe per raggiungere Capalbio, se pedalassero senza interruzioni.
[55 min; 17 min; 31 min; 107 min;1 h 31 min; 19 h 01 min]
[54 km; 6,8 h]
13
★★★
lA veloCItà
19
★★★
Dopo uno spettacolo, per raggiungere l’uscita un cantante deve percorrere un corridoio lungo 14,3 m, pieno di
fan che chiedono l’autografo. Dopo 51,5 min il cantante
riesce a uscire dal corridoio.
▶ Qual è stata la velocità media del cantante nel percorrere il corridoio?
[4,63 mm/s]
14
★★★
▶ Con quanti metri di distacco?
[Williams; 22 m]
20
★★★
a
Durante la 15 tappa del Giro d’Italia 2010 Ivan Basso ha pedalato per 6 h 21 min 58 s alla velocità media
di 35,186 km/h.
▶ Quanto era lunga la tappa?
[224 km]
15
★★★
Un aereo di linea parte dall’aeroporto di Venezia alle
11 h 45 min e giunge a Dublino alle 14 h 30 min. La distanza Venezia-Dublino è di 2037 km.
▶ Calcola la velocità media dell’aereo.
[741 km/h]
16
★★★
Per raggiungere la palestra dove si allena, Serena usa abitualmente lo scooter. Nel rispetto del limite di velocità
urbano, mantiene una velocità di 36 km/h impiegando 10 min da casa alla palestra.
▶ Calcola la distanza dalla casa di Serena alla palestra.
▶ Calcola quanto tempo impiegherebbe andando in bi-
A 1,0 km dal traguardo, in una prova all’autodromo di Monza, la Williams in seconda posizione corre a 262 km/h. La McLaren, in testa con un vantaggio
di 100 m, corre a una velocità media di 230 km/h.
▶ Chi vince la prova?
Nelle fasi provinciali dei campionati studenteschi di corsa
campestre lo studente A percorre la distanza di 12,0 km
alla velocità media di 4,75 m/s. Lo studente B percorre la
stessa distanza alla velocità media di 4,61 m/s.
▶ Calcola dopo quanti secondi, rispetto allo studente A,
taglia il traguardo lo studente B.
[8 × 10 s]
4
21
★★★
GRAfICI sPAzIo-teMPo e veloCItà
teMPo
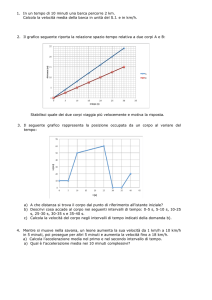
Considera il seguente grafco spazio-tempo.
posizione x (m)
3
0
t1
istante di tempo t (s)
t2
21
ESERCIZI
RICHIAMI suI MotI e le foRze
▶ Calcola la velocità media del moto tra gli istanti indicati.
25
★★★
Osserva il grafco spazio-tempo della fgura seguente:
140
22
★★★
posizione (km)
[0,17 m/s]
Considera il grafco spazio-tempo della fgura seguente.
Nel punto P è disegnata la retta tangente al grafco.
120
100
80
60
40
20
posizione x (m)
0
0
contrano.
26
★★★
3,5
[1 h; −20 km/h, 40 km/h]
Osserva il grafco spazio-tempo della fgura seguente:
posizione x (km)
Osserva il grafco velocità-tempo della fgura seguente.
velocità v (m/s)
3
250
corrisponde a P.
7
6
5
4
3
2
1
D
200
E
150
B
100
C
50
A
0
0
F
1
2
3
4
5
6
7
8
9
istante di tempo (h)
▶ Descrivi a parole come si muove il corpo rappresentato nel grafco al passare del tempo.
▶ Calcola la velocità nel tratto AB e nel tratto EF.
1
0
2
3
4 5 6 7 8
istante di tempo t (s)
9
10 11
▶ Descrivi a parole come varia la velocità del corpo in
movimento al trascorrere del tempo.
[100 km/h; −100 km/h]
27
★★★
Osserva il grafco spazio-tempo della fgura seguente:
posizione (m)
2,5
istante di tempo t (s)
▶ Trova la velocità istantanea del moto nell’istante che
24
2
▶ Calcola la velocità di A e di B nell’istante in cui si in-
to P?
★★★
1,5
▶ Determina l’istante in cui A (colore rosso) e B (colore
▶ Quale istante e quale posizione sono relative al pun-
★★★
1
blu) si incontrano.
0
23
0,5
istante di tempo (h)
P
160
140
120
100
80
60
40
20
0
Francesco è appassionato di escursionismo; durante le
vacanze ha percorso sull’Appennino, alle sorgenti del
Secchia, circa 2,5 km per raggiungere un rifugio. Una
volta arrivato, si è fermato per 15 min, poi è ripartito e
ha impiegato 1 h per il ritorno, ripercorrendo lo stesso sentiero dell’andata. In totale, considerando l’andata, il ritorno e la pausa, ha impiegato complessivamente 2 h 45 min.
▶ Calcola la velocità media sull’intero percorso in m/s.
▶ Calcola la velocità media all’andata e quella al ritorno.
▶ Rappresenta la situazione con un grafco spazio-tem0
2
4
6
8
10
po.
12
[0,56 m/s; 0,46 m/s; 0,69 m/s]
istante di tempo (s)
▶ Determina dal grafco la posizione dopo 8 s.
▶ Calcola la velocità nell’intervallo di tempo defnito da
5
▶ Calcola la velocità nell’intervallo di tempo defnito da
★★★
t1 = 0 s e t 2 = 4 s.
t1 = 0 s e t 3 = 8 s.
▶ Cosa puoi concludere?
[120 m; 15 m/s; 15 m/s]
28
Il Moto RettIlIneo unIfoRMe
Un’automobile si muove
di 30,0 m/s. Calcola:
▶ la velocità in km/h;
alla
velocità
costante
▶ quanto tempo impiega a percorre 50,0 km.
[108 km/h; 0,463 h]
22
ESERCIZI
RICHIAMI suI MotI e le foRze
29
★★★
Alice e Giulia, terminato l’allenamento, partono dalla palestra in momenti diversi. Alice a bordo del suo scooter
viaggia alla velocità costante di 30 km/h. Dopo 10 min,
Giulia alla guida della sua auto procede alla velocità costante di 50 km/h. Calcola:
▶ dopo quanto tempo Giulia raggiunge Alice;
35
★★★
Nella prima parte della gara un centometrista parte da
fermo e aumenta la sua velocità, con un’accelerazione
media di 4,9 m/s2, fno alla velocità v1 = 9,3 m/s.
▶ Quanto vale l’intervallo di tempo in cui avviene l’accelerazione?
[1,9 s]
▶ quale distanza hanno percorso Alice e Giulia quando
36
si incontrano.
★★★
Considera il seguente grafco velocità-tempo.
4
30
★★★
velocitˆ v (m/s)
[15 min; 1,2 × 10 m]
Anna e Lucia sono al parco; per salutarsi partono contemporaneamente dalle due estremità di un viale rettilineo, lungo 80 m, muovendosi l’una verso l’altra a velocità costante. La velocità di Anna è 1,4 m/s mentre la
velocità di Lucia è 1,2 m/s. Calcola:
▶ dopo quanto tempo Anna e Lucia si incontrano;
0
▶ quanti metri ha percorso Anna e quanti ne ha percor-
Un ciclista percorre una strada rettilinea pianeggiante
per 12 km in 10 min a velocità costante.
▶ Calcola quanti km percorre in 25 min alla stessa velocità.
Un’auto attraversa un incrocio alla velocità costante di 54 km/h; nello stesso momento una moto si trova 1,4 km più avanti e mantiene una velocità di 29 km/h.
Calcola:
▶ quanto tempo impiega l’automobilista a raggiungere
la moto;
▶ a che distanza dall’incrocio si trovano i veicoli quando
37
★★★
34
Martina sta andando a scuola a piedi e cammina su una
strada rettilinea alla velocità di 2,2 m/s. Per raggiungere
un’amica aumenta la sua velocità fno a 4,0 m/s in 6 s, poi
insieme proseguono a velocità costante per 5,0 min raggiungendo la scuola che dista 750 m dal punto del loro
incontro.
▶ Calcola l’accelerazione media di Martina.
[0,3 m/s2; 2,5 m/s]
38
★★★
l’ACCeleRAzIone
Un gatto sta inseguendo un topo. Parte da fermo e, proseguendo in linea retta, in 4,0 s raggiunge la velocità
di 6,0 m/s, prosegue a velocità costante per 6,0 s e si ferma in 2,0 s aferrando il topo.
▶ Calcola il valore dell’accelerazione nei primi 4,0 s del
moto.
▶ Calcola il valore dell’accelerazione negli ultimi 2,0 s.
▶ Rappresenta la situazione in un diagramma veloci-
Una ragazza su uno skateboard parte su una strada pianeggiante con una velocità di 4,2 m/s. A causa degli attriti, dopo 5,5 s la sua velocità è di 1,6 m/s.
▶ Quanto vale l’accelerazione media dello skateboard?
[−0,47 m/s2]
★★★
9
scuola.
[2,0 × 102 s; 3,0 × 103 m]
33
8
▶ Calcola la velocità delle ragazze per raggiungere la
avviene il sorpasso.
★★★
3
4
5
6
7
istante di tempo t (s)
[1,1 m/s2]
[30 km]
6
2
di tempo defnito da tali punti.
zio-tempo e in uno velocità-tempo.
32
1
▶ Calcola l’accelerazione media del moto nell’intervallo
▶ Rappresenta la situazione in un diagramma spa-
★★★
B
fco.
[31 s; 43 m; 37 m]
★★★
C
▶ Determina le coordinate dei due punti B e C sul gra-
si Lucia.
31
7
6
5
4
3
2
1
Un treno procede su un binario rettilineo alla velocità
vi = 80,2 km/h. Poi accelera per 3,80 s con un’accelerazione costante di 1,10 m/s2.
▶ Qual è la velocità fnale del treno, espressa in kilometri all’ora?
tà-tempo.
[1,5 m/s2; −3,0 m/s2]
39
★★★
Un ragazzo in moto, in prossimità di un incrocio, passa da una velocità di 72 km/h a una di 36 km/h in 20 s.
Calcola:
▶ l’accelerazione della moto in frenata;
▶ il tempo necessario perché la moto si fermi nell’ipotesi
di accelerazione costante.
[−0,50 m/s2; 20 s]
[95,2 km/h]
23
ESERCIZI
40
★★★
RICHIAMI suI MotI e le foRze
In una gara di Formula 1, la Ferrari e la Mercedes partono contemporaneamente da ferme.
La Ferrari ha un’accelerazione di 12 m/s2 e la Mercedes
di 11 m/s2.
Determina:
▶ la legge della velocità della Ferrari e della Mercedes;
▶ la velocità della Ferrari e della Mercedes dopo 3,0 s;
▶ quanto tempo impiega la ragazza a raggiungere il pullman;
▶ quale velocità possiede quando lo raggiunge.
[8,7 s; 3,5 m/s]
46
★★★
▶ il tempo impiegato dalla Mercedes per raggiungere la
velocità che ha la Ferrari dopo 3,0 s.
Un ciclista sta percorrendo un tratto rettilineo quando in
lontananza vede un semaforo rosso e inizia a rallentare
sino a fermarsi. Il moto del ciclista è descritto dal grafco
rappresentato.
12
[36 m/s; 33 m/s; 3,3 s]
41
★★★
velocità v(m/s)
10
Osserva il grafco velocità-tempo della fgura seguente.
10
C
velocitˆ v (m/s)
8
6
H
4
2
0
2
B
2
D
0
3
4
6
9
12
15
18 21
E
G
24
27 30
33
[1,7 m/s2; −2,0 m/s2]
47
★★★
[0 m/s2; 1 m/s2; −1 m/s2; 0 m/s2; −1 m/s2; 1 m/s2]
Il Moto RettIlIneo
unIfoRMeMente ACCeleRAto
Un ciclista parte da fermo e percorre 24 m in 10 s.
▶ Calcola la sua accelerazione media.
[1,7 s; 17 m/s]
48
★★★
★★★
Alessio sta camminando alla velocità di 1,3 m/s per raggiungere la fermata dell’autobus. Si accorge di essere in
ritardo, così inizia a correre raggiungendo la velocità
di 2,5 m/s in 3 s. Calcola:
▶ l’accelerazione media di Alessio;
▶ la distanza percorsa nei 3 s.
44
★★★
▶ la distanza percorsa nello sprint fnale.
[15 m/s; 1,3 × 102 m]
45
★★★
24
Una ragazza inizia a correre da ferma con un’accelerazione a=0,40 m/s2 per raggiungere il pullman che sta partendo. La fermata è distante 15 m dalla ragazza. Calcola:
Andrea lascia cadere un sasso in un pozzo. Dopo 3,0 s
sente il tonfo. La velocità del suono in aria è 340 m/s.
▶ Calcola quanto è profondo il pozzo.
[3 × 10 m]
8
49
★★★
lA foRzA-Peso
Paolo pesa 686 N.
▶ Calcola la massa di Paolo.
[70 kg]
[0,4 m/s2; 6 m]
Un ciclista sta pedalando alla velocità di 36 km/h. Durante lo sprint fnale aumenta la sua velocità e per 10 s
mantiene l’accelerazione di 0,50 m/s2. Calcola:
▶ la velocità con cui il ciclista taglia il traguardo;
Un muratore in un cantiere sta sistemando alcune tegole
sul tetto di una casa alta 15 m, quando inavvertitamente una tegola cade a terra. Trascurando l’attrito dell’aria,
calcola:
▶ in quanto tempo la tegola raggiunge il suolo;
▶ con quale velocità la tegola giunge a terra.
[0,48 m/s2]
43
12
nell’intervallo da 6,0 s a 11,0 s.
istante di tempo t (s)
▶ Per ogni tratto, calcola l’accelerazione.
42
10
▶ Calcola l’accelerazione mantenuta nei primi 6,0 s e
F
movimento al trascorrere del tempo.
★★★
8
▶ Descrivi il moto.
36
▶ Descrivi a parole come varia la velocità del corpo in
7
6
istante di tempo t(s)
Ð2
Ð4
6
0
4 A
0
8
50
★★★
Un bambino sta giocando con la palla sul balcone di casa.
Urta un vaso di fori di massa 550 g che cade a terra.
▶ Calcola la forza-peso che agisce sul vaso di fori.
[5,4 N]
51
★★★
Sulla Luna la forza-peso è circa 1/6 di quella sulla Terra. Calcola:
▶ il valore di g sulla Luna;
▶ il peso di 1,0 kg di mele sulla Luna e sulla Terra.
[1,6 m/s2 ; 1,6 N; 9,8 N]
RICHIAMI suI MotI e le foRze
52
★★★
Un ragazzo ha una massa di 75 kg. Uscito dalla palestra,
si carica in spalla la borsa sportiva a tracolla. La forza-peso complessiva è 784 N. Calcola:
▶ la forza-peso del ragazzo;
▶ la massa della borsa sportiva.
▶ Calcola la costante elastica della molla.
[5,0 × 102 N/m]
60
★★★
[7,4 × 102 N; 5 kg]
53
★★★
ESERCIZI
Su Giove l’accelerazione di gravità vale 25 m/s2. Calcola:
▶ la forza-peso su Giove di una persona di massa 80 kg;
Ciascuna delle 4 molle identiche degli ammortizzatori di
una citycar di massa 1000 kg subisce una deformazione
di 4 cm a causa del peso dell’auto. Sull’auto salgono dei
passeggeri che hanno una massa complessiva di 250 kg.
▶ Calcola la deformazione degli ammortizzatori quando
sono a bordo i passeggeri.
[5 cm]
▶ la massa corrispondente a tale forza-peso sulla Terra.
[2,0 × 103 N; 2,0 × 102 kg]
54
★★★
Una cassa di patate di massa 20 kg si trova su un piano
inclinato che forma con l’orizzontale un angolo di 30°.
▶ Calcola il peso della cassa e le sue componenti parallela e perpendicolare al piano.
10 lA foRzA dI AttRIto
61
★★★
[2,0 × 102 N; 98 N; 1,7 × 102 N]
9
[2,5 × 102 N]
lA foRzA dI Hooke
62
55
★★★
Una molla di costante elastica 70 N/m subisce una deformazione di 14 cm.
▶ Calcola l’intensità della forza applicata.
★★★
[9,8 N]
56
★★★
Una molla viene compressa di 3,0 cm da una forza
di 3,0 N.
▶ Calcola la costante elastica della molla.
63
★★★
[1,0 × 10 N/m]
57
Una molla subisce una deformazione di 10 cm per efetto
di una forza di 3,0 N. Calcola:
▶ il valore della costante elastica della molla;
[4,3 × 102 N; 0,38]
di 15 cm.
64
★★★
58
★★★
Fabio deve spostare un baule di 80 kg fermo nella sua
stanza. Il coefciente di attrito statico tra baule e pavimento è 0,55. Fabio decide di inserire tra pavimento e
baule un panno di lana; in queste condizioni la forza di
primo distacco è di 300 N. Calcola:
▶ la forza di attrito al distacco senza panno;
▶ il coefciente di attrito quando viene inserito il panno.
▶ l’intensità della forza che provoca una deformazione
[30 N/m; 4,5 N]
In un magazzino di generi alimentari si deve spostare
una cassa di sughi di pomodoro. L’operaio addetto applica in orizzontale alla cassa una forza di 141 N per metterla in moto; il coefciente di attrito statico tra il pavimento e la cassa è 0,32.
▶ Calcola la massa della cassa dei sughi di pomodoro.
[45 kg]
2
★★★
L’imbianchino per poter tinteggiare le pareti di una stanza deve spostare un armadio di 50 kg. Il coefciente di attrito statico tra il pavimento e l’armadio è 0,50.
▶ Calcola l’intensità della forza con cui l’imbianchino
agisce per spostare l’armadio.
Durante un’esercitazione di laboratorio, un gruppo di studenti dispone di una molla di costante elastica 31 N/m, lunga 22,0 cm quando è a riposo. Successivamente, la molla caricata con un pesetto subisce una
deformazione e raggiunge la lunghezza di 30,0 cm.
▶ Calcola la massa del pesetto applicato alla molla.
Un corpo di massa 2,5 kg, inizialmente fermo, scivola su
un piano in presenza di attrito. Il coefciente di attrito
statico è 0,30 e il coefciente di attrito dinamico è 0,15.
Calcola:
▶ la forza che permette al corpo di iniziare a muoversi.
▶ la forza immediatamente dopo il distacco.
[7,4 N; 3,7 N]
[0,25 kg]
65
59
★★★
La tabella che segue riporta i valori della deformazione
di una molla.
x(cm)
1,0
2,0
3,0
4,0
5,0
F(N)
5
10
15
20
25
Rappresenta grafcamente i dati della tabella.
★★★
In una pausa di studio, due ragazzi posano una moneta
sul libro di matematica e lo inclinano per vedere quando
la moneta inizierà a scendere. Il coefciente di attrito statico tra la copertina del libro e la moneta è 0,46.
▶ Calcola il valore dell’angolo di inclinazione dopo il
quale la moneta inizia a scivolare.
[25°]
25