Limiti di Funzioni

LIMITI DI FUNZIONI
SALVATORE MODICA
Sommario.
Definizioni ed esempi
Approssimazione al limite
Risultati sui limiti: I
Esempi ed esercizi: I
Risultati sui limiti: II
Esempi ed esercizi: II.
DEFINIZIONI ED ESEMPI
Pensiamo alla definizione di limite per le successioni, che sono funzioni
con dominio N+ . Per esempio per an → ∞, la definizione dice che per
ogni K esiste un punto nK nel dominio di (an ) a partire dal quale —
nella ‘direzione di movimento’ di n— la funzione/successione ha valori
maggiori di K. Lo stesso per an → l: a partire da un nǫ la funzione
dista da l meno di ǫ. Per le funzioni che non sono successioni l’idea resta
la stessa. Di diverso c’è che mentre n non può che andare a infinito,
la x può tendere a infinito, a meno infinito, o ad un valore finito. E
poi n ‘saltella’ lungo la retta, mentre x si muove con continuità (per
visualizzare, immagina una circonferenza che rotola su una retta: il
punto di contatto fra le due si muove con continuità sulla retta).
I casi di x → ∞ ed x → −∞ sono i più simili alle successioni, e da
questi cominciamo. Per esempio, limx→−∞ f (x) = ∞. Intuitivamente
l’idea è che f supera qualunque prefissato valore (altezza) purchè x
sia sufficientemente ‘lontano’ nella direzione di movimento (cioè verso
sinistra). Formalmente: limx→−∞ f (x) = ∞ se per ogni K ∈ R esiste
xK tale che ∀x < xK si ha f (x) > K. Come per le successioni, e per
lo stesso motivo, basta considerare i K > K per un arbitrario K, per
esempio zero, e dire dunque “∀K > 0” invece di “∀K ∈ R”.
Analogamente, limx→∞ f (x) = −∞ se per ogni M ∈ R esiste xM
tale che ∀x > xM si ha f (x) < M. Qui basta considerare M < 0;
pensando K come positivo e quindi M come −K, possiamo allora dire:
limx→∞ f (x) = −∞ se per ogni K > 0 esiste xK tale che ∀x > xK si ha
f (x) < −K. Cosı̀ la lettera K indicherà sempre un numero positivo;
questo torna comodo nelle disequazioni.
Date: 6.XII.97, 3.XI.98. Univ. di Palermo, Istituto di Matematica per la R.O.
1
LIMITI DI FUNZIONI
2
Ancora, limx→∞ f (x) = l: quando x si muove verso destra, la distanza (verticale nelle figure) fra f ed l diventa minore di qualunque
prefissato valore (che sarà ǫ), purchè si aspetti abbastanza; cioè: per
ogni ǫ > 0 esiste xǫ tale che ∀x > xǫ risulta |f (x) − l| < ǫ. E’ quasi
superfluo osservare che per verificare f → l basta considerare ǫ < ǫ
qualunque.
Si scrivano le altre definizioni per x tendente a più o meno infinito
(i casi sono x → ±∞ con limite l ∈ R o ±∞).
(1) Un punto su cui abbiamo sorvolato è: quando diciamo “∀x >
xǫ risulta |f (x) − l| < ǫ”, ovviamente tutte queste x devono essere nel
dominio di f , altrimenti la definizione non ha senso. Analogo il caso di
x → −∞.
NOTE.
(2) Per scrivere le negazioni delle definizioni di limite (tipo “non è
vero che limx→∞ f (x) = l”) servono le negazioni di espressioni come
“per ogni ǫ > 0 succede che. . . ” o “esiste xk tale che. . . ”; queste si
fanno cosı̀: se P è una frase, indichiamo con ¬P la sua negazione (se P
è “mangio” ¬P è “non mangio”); qual è la negazione di “ogni giorno
mangio”? E’: “esiste un giorno in cui non mangio”. E se P(x) è “sono
ricco nel giorno x”, qual è la negazione di “esiste un x tale che P(x)”?
E’: “per ogni x, ¬P(x)”. Stiamo usando queste equivalenze logiche:
¬ ∀x P(x)
⇔ ∃x tale che ¬P(x)
¬ ∃x tale che P(x)
⇔ ∀x ¬P(x).
In pratica, per verificare un limite si fa come per le successioni:
si vede se la disequazione rilevante è soddisfatta per le x che vogliamo.
ESEMPI.
(a) f (x) = ax + b, una retta; vediamola con a < 0. Per x → ∞:
ax+ b < −K ⇔ x > (−K −b)/a = xK , dunque limx→∞ (ax+ b) = −∞.
Analogamente limx→−∞ (ax + b) = ∞.
(b) f (x) = ax2 , parabola. Prendiamo a > 0: sembra limx→∞ f =
limx→−∞
K > 0), ax2 p
> K se
p = ∞, e in effetti (prendendo come sempre
p
x > K/a, che verifica il primo (con
pxK = K/a), e se x < − K/a,
che verifica il secondo (con xK = − K/a).
Usando l’esercizio 3 si trovano per f (x) = ax2 + bx + c gli stessi
risultati (ovvi dai disegni) scrivendo ax2 + bx + c = y0 + a(x − x0 )2 .
(c) Un’iperbole, f (x) = α/x; vogliamo esaminarne il comportamento
per x → ±∞ (ogni altra iperbole ha comportamento analogo per
l’esercizio 4). Poichè |α/x| < ǫ ⇔ |x| > |α|/ǫ, è limx→±∞ α/x = 0.
Di α/x, pensiamo per esempio ad α > 0, vorremmo anche dire che
‘tende a infinito per x che va a zero da destra, ed a meno infinito per
x che va a zero da sinistra. Lo faremo fra poco.
(d) limx→∞ f (x) = limx→−∞ f (−x), e limx→−∞ f (x) = limx→∞ f (−x).
Facciamo la prima, per esempio con limx→∞ f (x) = l: dato ǫ, per
LIMITI DI FUNZIONI
3
x > xǫ si ha |f (x) − l| < ǫ; dunque per x < −xǫ |f (−x) − l| < ǫ (se
questa verifica ti sembra troppo breve, chiama g : x 7→ f (−x) e verifica
che l’xǫ richiesto per g, xgǫ è l’opposto dell’ xǫ esistente per f, xfǫ ).
(e) Funzioni esponenziali f (x) = ax . Per a > 1: ax > K ⇔ x >
loga K = xK , dunque limx→∞ ax = ∞. E |ax | < ǫ ⇔ ax < ǫ ⇔ x <
loga ǫ = xǫ , dunque limx→−∞ ax = 0. Il caso 0 < a < 1 è altrettanto
facile, e comunque sappiamo dall’esempio precedente che deve essere
limx→−∞ ax = ∞ e limx→∞ ax = 0. Questo somiglia molto a quanto
fatto con le successioni: “Se xn → ∞, allora per a > 1 è axn → ∞”,
eccetera; ricordi? Bene, c’è più che una somiglianza; lo vedremo meglio.
(f) Accertati che limx→∞ loga x è come sembra. Soluzione in nota (non
guardare subito). 1
(g) Disegna due funzioni potenza f (x) = xα , una con α > 0 e una
con α < 0, e verifica che i limiti per x → ∞ sono quelli che i grafici
suggeriscono; soluzione in nota. 2
(h) Per n intero si può considerare anche limx→−∞ xn . Indoviniamo
dai grafici; per verificare: 3 se n è pari√xn = (−x)n ; √
prendi x < 0 e
n
n
n
n
K > 0, cosı̀ x = (−x) > K ⇔ −x > K ⇔ x < −
K = xK , cioè
√
n
n
limx→−∞ f = ∞. Se n è dispari x < −K ⇔ x < −K, e il limite
vale −∞.
Se n intero dispari possiamo fare pure limx→−∞ x1/n . Come sopra,
verifica che il limite è −∞.
√
√
(i) limx→∞ ( x + 1 − x) = 0. L’abbiamo visto con√le successioni.
√
Vogliamo
|f
(x)|
=
f
(x)
<
ǫ
per
x
>
x
.
Ma
f
(x)
=
1/(
x
+
1+
x) ≤
ǫ
√
2
1/(2 x) < ǫ per x > 1/4ǫ = xǫ .
Fin qui, rispetto a quanto visto per le successioni si può dire che abbiamo solo cambiato nome ad n ed an , chiamandole x ed f (x). Qualcosa
di nuovo (ma non troppo) si vede considerando x che tende ad un valore
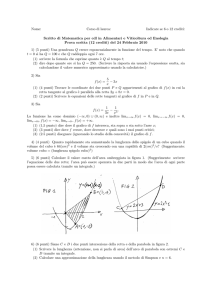
finito, come nei grafici di 1/x ed 1/|x| riportati nella prossima figura.
Cominciamo da 1/x, e immaginiamo x positivo che va verso 0, cosa
che scriviamo come x → 0+ . 4 Vogliamo dire che f tende a infinito,
e l’idea è la stessa di sempre: comunque fissato K, camminando lungo
l’asse delle x verso zero (da destra) ci sarà un punto a partire dal
quale la f sta sopra K. In altre parole, limx→0+ f (x) = ∞ se dato
K > 0 esiste xK tale che per ogni x ∈ (0, xK ) si ha f (x) > K. Nota
che richiediamo 0 < x < xK , non 0 ≤ x < xK : stiamo esaminando
1Se
a < 1 è loga x < K per x > aK = xK , quindi limx→∞ loga x = −∞;
analogamente si vede che limx→∞ loga x = ∞ se a > 1.
2Per α > 0, xα > K ⇔ x > K 1/α = x , dunque lim
α
K
x→∞ x = ∞. Per α < 0 si
α
−1 −α
α
può scrivere x = (x )
per verificare che limx→∞ x = 0.
3usando la proposizione del paragrafo ‘Ancora sulle potenze ad esponente intero’
di UiN
4x → 0+ abbrevia (x → 0)+ , cioè il + si riferisce ad x → 0, non a 0.
LIMITI DI FUNZIONI
6
4
6
-
Grafico di x−1
-
Grafico di |x|−1
cosa fa la f per x vicino a zero, non uguale. Per esempio nella figura
da cui siamo partiti, in x = 0 la f non è nemmeno definita. Nota
anche il K > 0 che è più comodo ma equivalente; questo fatto non lo
menzioneremo più, a partire dal prossimo capoverso.
Se d’altra parte facciamo tendere x a 0 da sinistra (scritto x → 0− ),
intuitivamante f tende a meno infinito, perchè: per ogni K > 0 esiste
xK tale che per ogni x ∈ (xK , 0) si ha f (x) < −K. E questa è la
definizione di limx→0− f (x) = −∞.
Nota. Nel considerare il limite di una f per x → x+
0 abbiamo supposto che esiste un intervallo (x0 , x0 + δ) ⊆ Df ; discorso discorso analogo per x → x−
0 . In effetti, che senso avrebbe considerare il limite di
log x per x → 0− , o per x → −3?
Nello stesso spirito, quando faremo x → x0 supporremo che il dominio di f contiene sia un intorno sinistro di x0 che uno destro (anche
se non necessariamente il punto x0 stesso).
(a) limx→0− 1/x = −∞, perchè: abbiamo 1/x < −K ⇔ 0 >
x > −1/K = xK . Fai i limiti di α/x per x → 0+ ed x → 0− , con
α ≷ 0. Questo completa il quadro per le iperboli.
ESEMPI.
(b) Le funzioni potenza con esponente negativo sono del tipo 1/xα con
α > 0 (abbiamo considerato α = 1 sopra). E’ limx→0+ 1/xα = ∞,
perchè 1/xα > K ⇔ 0 < x < (1/K)1/α = xK . Delle funzioni potenza
per x → 0+ resta da vedere quelle con esponente positivo (vedi prossimo
esempio (a)).
Il caso di 1/|x| ha di diverso che comunque facciamo tendere x a zero
—da destra o da sinistra— la f va a infinito. Nei casi come questo,
cioè se esistono i limiti destro e sinistro e sono uguali, diciamo che
esiste limx→0 f (x), con quel valore comune. Nel nostro caso, poichè
limx→0+ f (x) = limx→0− f (x) = ∞, è limx→0 f (x) = ∞. Nota che ciò
è equivalente a dire che per ogni K > 0 esiste un xK tale che per
LIMITI DI FUNZIONI
5
−xK < x < xK , x 6= x0 (cioè 0 < |x| < xK ), f (x) > K. (perchè:
supponiamo che i due limiti destro e sinistro esistono e sono uguali.
Allora limx→0+ f (x) = ∞ implica che esiste un xdK tale che f (x) > K
per 0 < x < xdK ; limx→0− f (x) = ∞ implica che esiste un xsK tale che
f (x) > K per xsK < x < 0; quindi posso prendere xK = min{xdK , −xsK }.
Viceversa se per ogni K esiste un xK tale che per 0 < |x| < xK ,
f (x) > K, posso prendere xdK = xsK = xK ).
Se x → x0 la 0 < |x| < xK viene sostituita da 0 < |x − x0 | < xK . Per
ricordare che più grande K più piccolo deve generalmente essere xK si
indica quest’ultimo con δK (δ ed ǫ sono le lettere dei numeri piccoli);
sicchè: limx→x0 f (x) = ∞ se per ogni K > 0 esiste δK tale che per
0 < |x − x0 | < δK è f (x) > K.
Pensiamo infine al grafico di f (x) = x2 , e facciamo andare x a 2.
Qui per x → 2 la f tende ad un valore finito (4, che non ha niente
di speciale). La definizione è allora (disegna): limx→x0 f (x) = l se per
ogni ǫ > 0 esiste δǫ > 0 tale che per 0 < |x−x0 | < δǫ si ha |f (x)−l| < ǫ.
Nota il ”0 <”: nella definizione di limite non si pone alcuna restrizione
su f in x0 (cfr. l’esempio (c) qui sotto). Per esercizio si definiscano i
limiti sinistro e destro per questo caso.
Ricapitolando, abbiamo visto tre tipi di limiti: (i) x → ±∞, dove
tutto è come per le successioni; (ii) x → x0 ∈ R ed f → ±∞; (iii)
x → x0 ∈ R ed f → l ∈ R. Accertati di saperle scrivere tutte.
ESEMPI.
(a) limx→x0 x = x0 : con δǫ = ǫ.
(b) Per α > 0, limx→0+ xα = 0, perchè xα < ǫ ⇔ 0 < x < ǫ1/α = δǫ .
(c) Considera


2x x < 0
f (x) = 3
x=0

x x > 0.
Qui limx→0 f (x) = 0 (anche se f (0) = 3). La verifica dei limiti destro
e sinistro è immediata.
(d) Determina a ∈ R tale che esista limx→3 f (x) per la funzione
(
2x + 1 x < 3
f (x) =
x + a x > 3.
Si verifichi che limx→3− f (x) = 7 e limx→3+ f (x) = 3 + a; dunque a = 4.
√
(e) Verifichiamo che limx→1 ( x − 1)/(x − 1) = 1/2. Si ha
f (x) − 1 = 1 −√x = |x −√1| < |x − 1|,
2
2
2(1 + x) 2(1 + x)2
dunque possiamo prendere δǫ = ǫ.
LIMITI DI FUNZIONI
6
Nota che con la maggiorazione si ottiene un δǫ più che sufficiente
perchè |f (x) − l| < ǫ (considera la g(x) = |f (x) − l| e vedilo prima di
tutto graficamente). In questo esempio se si risolve |f (x) − 1/2| < ǫ
1−2ǫ 2 1+2ǫ 2
si ottiene (con ǫ < 1/2) δǫ = min{1 − ( 1+2ǫ
) , ( 1−2ǫ ) − 1}, che si può
verificare essere maggiore di ǫ per ǫ < 1/2.
= 4. Vogliamo δǫ tale che per |x − 2| < δǫ si abbia
(f) limx→2 x+2
x−1
x−2
|f (x) − 4| = 3| x−1
| < ǫ. Prendendo per esempio |x − 2| < 1/2, è
x−2
|x − 1| = x − 1 > 1/2, dunque 3| x−1
| < 6|x − 2|. Dunque δǫ =
min{1/2, ǫ/6} va bene.
(g) limx→x0 sin x = sin x0 . Si fa con le formule di prostaferesi, come
abbiamo fatto con cos xn : per 0 < |x| < π/2 si ha | sin x − sin x0 | =
0
0
0
|·| cos x+x
| ≤ 2| sin x−x
| ≤ |x−x0 |; dunque | sin x−sin x0 | <
2| sin x−x
2
2
2
ǫ per |x − x0 | < min{π/2, ǫ}.
Allo stesso modo si vede limx→x0 cos x = cos x0 . E si può verificare
per esercizio che limx→π/2− tan x = ∞, sfruttando limx→π/2− cos x =
cos π/2 = 0 ed il fatto che per x vicino a π/2 è sen x > 1/2. Soluzione
in nota. 5
E’ anche limx→−π/2+ tan x = −∞. 6 Dalla periodicità della tangente
deduciamo allora anche limx→π/2+ tan x = −∞. In particolare non
esiste limx→π/2 tan x perchè i limiti destro e sinistro esistono ma sono
diversi.
(h) Per x0 > è limx→x0 log x = log x0 (ricorda che ‘nel discreto’ xn →
x0 ⇒ log xn → log x0 ; la presente verifica è analoga). Soluzione in
nota. 7
(i) Una condizione ‘di Cauchy’ per l’esistenza del limite: se esiste l =
limx→x0 f (x) allora ∀ǫ esiste δǫ tale che ∀x, x′ ∈ (x0 − δǫ , x0 + δǫ ) \ {x0 }
si ha |f (x) − f (x′ )| < ǫ. Perchè |f (x) − f (x′ )| ≤ |f (x) − l| + |f (x′ ) − l|.
(j) Applicazione dell’esempio precedente: non esiste limx→0 f per
(
1
x≤0
f (x) =
1
sen x x > 0.
Qui il limite non esiste perchè non esiste limx→0+ sen x1 : in ogni intervallo (0, δ) ci sono x, x′ tali che sen x1 −sen x1′ = 2 (x = 1/(2kπ + π2 ), x′ =
1/(2kπ + 23 π) per k grande abbastanza).
5Sia
K > 0 arbitrario; per x ∈ ( π6 , π2 ) sin x > 12 ; sia δ tale che per x ∈ ( π2 − δ, π2 )
risulti 0 < cos x < 1/2K (δ esiste perchè limx→π/2 cos x = 0); definiamo δK =
1
min{ π6 , δ}. Per x ∈ ( π2 − δK , π2 ) è allora tan x > 2 cos
x > K.
6Questo si può verificare direttamente, oppure dedurre dall’esercizio 5 (perchè
tan x = − tan(−x)).
7Vogliamo −ǫ < log x − log x < ǫ; al centro c’è log(x/x ); mettendo tutto ad
0
0
esponente di e, moltiplicando per x0 e poi togliendo x0 si ottiene l’equivalente −δ s ≡
−x0 (1 − e−ǫ ) < x − x0 < x0 (eǫ − 1) ≡ δ d , sicchè basta prendere δǫ = min{δ s , δ d }.
LIMITI DI FUNZIONI
7
(k) limx→±∞ arctan x = ±π/2. Questo non siamo ancora in grado di
dimostrarlo rigorosamente, ma lo vogliamo usare, quindi vediamo almeno una giustificazione. Prendiamo x → ∞: sia dato ǫ > 0; vogliamo
xǫ tale che per x > xǫ risulti π/2 − ǫ < arctan x < π/2 + ǫ; la seconda disugualgianza è sempre verificata; e poichè arctan x è crescente,
la prima è verificata per x > tan(π/2 − ǫ) = xǫ . 8
Possiamo incorniciare la definizione di limite che abbiamo usato in
tutti i casi visti. Per ξ ∈ R (può essere un x o un y) chiamiamo intorno
di ξ un intervallo tipo (ξ − δ, ξ + δ) (con δ > 0); se ξ = ∞, con lo stesso
termine indichiamo un intervallo tipo (a, ∞) con a ∈ R; se ξ = −∞ un
intervallo tipo (−∞, a). Allora:
Con x0 , l ∈ R, limx→x0 f (x) = l se per ogni intorno J di l
esiste un intorno IJ di x0 tale che per x ∈ IJ \ {x0 } si ha f (x) ∈ J.
DEFINIZIONE.
Controlla che le definizioni precedenti sono effettivamente tutte casi
particolari di questa. A proposito, come per le successioni la definizione
è ben posta, nel senso che: Se il limite esiste, è unico. La dimostrazione
(in nota) è come per le successioni. 9
Prima di andare avanti riguardiamo i risultati che abbiamo trovato
sulle funzioni fondamentali: abbiamo visto i limiti di ax per x → ±∞,
di loga x ed xα per x → ∞ ed x → 0+ e di x±n per x → 0− , x → −∞; i
limiti di sen x, cos x e tan x per x → x0 ∈ R e quelli per x → ±∞ —che
non esistono; quelli di tan x per x → ±π/2; e quelli di log x per x →
x0 > 0 (in pratica manca solo qualche limite per x → x0 ). Abbiamo
sempre trovato quello che ci attendevamo dal grafico, e d’altra parte,
alla luce dei risultati sulle successioni corrispondenti, ci saremmo stupiti
del contrario. Confermeremo che doveva essere cosı̀ nella ‘conseguenza’
(b) di pagina 12.
In molti degli esempi, in particolare quelli sulle funzioni fondamentali, abbiamo visto limx→x0 f (x) = f (x0 ), che cioè il limite esiste e
la funzione non ha una discontinuità, nel senso di un f (x0 ) ‘per i
fatti suoi’. In questo caso si dice appunto che f è continua in x0 .
Nota che limx→x0 f (x) = f (x0 ) se: per ogni ǫ > 0 esiste δǫ tale che
|x − x0 | < δǫ ⇒ |f (x) − f (x0 )| < ǫ; non c’è “0 < |x − x0 |”, perchè
|f (x) − f (x0 )| < ǫ è automaticamente soddisfatta in x0 . Sul concetto
torneremo, perchè sulla contiuità si fondano tutti i risultati importanti
del corso, dunque registriamo:
8Questa
non è una dimostrazione, perchè si è assunto, ma non dimostrato, che
il codominio di tan x è tutto R (altrimenti come potremmo essere sicuri che tutte
le x > tan(π/2 − ǫ) sono nel dominio di arctan x?). Ripareremo questa falla.
9Prima escludi che possa essere contemporaneamente f → l ∈ R ed f → ±∞, o
f → ∞ ed f → −∞; poi mostra che se f → l ed f → l′ con l, l′ ∈ R allora per ogni
ǫ > 0 risulta |l − l′ | < ǫ da cui l = l′ .
LIMITI DI FUNZIONI
8
Siano f : R → R ed x0 ∈ Df . f è continua in x0 se
∃ limx→x0 f (x) = f (x0 ), cioè il limite esiste e vale f (x0 ). Continuità su
A ⊆ Df vuol dire per ogni x0 ∈ A.
DEFINIZIONE.
Nota. Abbiamo sempre supposto che quando prendiamo il limite per x → x0 c’è
un intorno I di x0 tale che I \{x0 } ⊆ Df (o per prendere x → x+
0 con x0 ∈ R che un
intorno destro, cioè tipo (x0 , x0 +δ), sia contenuto in Df , e discorso analogo per x →
x−
0 ); questo va in pratica sempre bene, ma qualcuno può chiedersi: la definizione di
limite di successione, guardando la successione come una funzione con Df = N+ ,
è un caso particolare di limite di funzione? La domanda è legittima, e la risposta
in effetti è no, perchè Df = N+ non contiene nessun intervallo, quindi secondo
la nostra definizione non si può considerare il limite di una funzione–successione,
nè per x → x0 ∈ R (che è accettabile), nè per x → ∞ (che non lo è). A questa
situazione c’é un facile e naturale rimedio. Perchè l’operazione di limite per x →
x0 ∈ R abbia senso non occorre che sia verificata la nostra ipotesi di partenza, ma
basta: se x0 ∈ R, che ci siano punti di Df arbitrariamente vicini ad x0 ; se x0 = ∞
(risp. −∞), semplicemente che Df sia illimitato superiormente (risp. inferiormente).
Per tali punti possiamo modificare la definizione di limite richiedendo che per x
vicino ad x0 ed in Df la f sia vicino ad l. Cosı̀ per esempio per x → ∞, anche se
Df non contiene nessun intervallo (a, ∞) lungo il quale x possa ‘rotolare’, poichè
sup Df = ∞ la x può andare verso infinito saltellando lungo punti di Df (come
per le successioni). Formalmente, la condizione su x0 che abbiamo detto è: Ogni
intorno I di x0 ha I ∩ Df \ {x0 } 6= ∅ (Tali x0 si dicono ‘punti di accumulazione’ per
Df ). E la definizione di limite: Per x0 , l ∈ R, limx→x0 f (x) = l se per ogni intorno
J di l esiste un intorno IJ di x0 tale che per x ∈ IJ ∩ Df \ {x0 } sia f (x) ∈ J. Con
questa definizione i limiti di successioni sono casi particolari di limiti di funzioni.
Domanda: qual è il problema se applichiamo questa definizione ad un punto che
non è di accumulazione per Df ? 10
APPROSSIMAZIONE AL LIMITE
Abbiamo finora verificato relazioni di limite, cioè dato l’ǫ abbiamo trovato il δǫ ,
e cosı̀ via, e qui, per i più curiosi, faremo qualche altro esercizio di questo tipo.
Perchè? Quando avremo imparato a calcolare i limiti sarà immediato per esempio
trovare che limx→∞ (1− x1 + x12 ) = 1, ed a quel punto verrà spontaneo chiedersi: a che
serve verificarlo, se lo si conosce già? La risposta è che sono due cose diverse: una
cosa è sapere che limx→∞ f (x) = 1; ben altra è sapere quanto deve essere grande
x perchè risulti per esempio |f (x) − 1| < 3 · 10−6 . E’ evidente che quest’ultima
informazione è molto più precisa della sola conoscenza del valore del limite; ‘vale’
di più, sicchè non ci possiamo sorprendere del fatto che in genere ‘costa’ di più, cioè
è più difficile da ottenere. Inoltre, non tutte le informazioni hanno lo stesso valore:
immagina un matematico e un suo cliente interessato al comportamento asintotico
della funzione di sopra; il primo gli regala l’informazione “limx→∞ f (x) = 1”, ma
al secondo serve |f (x) − 1| < 3 · 10−6 ; supponi che il matematico scopra subito che
x > 1500 ⇒ |f (x)−1| < 3·10−6 ; questa è informazione che il cliente può pagare, ma
supponi adesso che quest’ultimo non può aspettare fino a 1500 (pensa ad x come
tempo); chiederà allora: “E prima, niente da fare?”, che il matematico traduce
in: “E’ vera anche l’implicazione opposta, |f (x) − 1| < 3 · 10−6 ⇒ x > 1500?”
La doppia implicazione vale molto più; la prima informazione diceva, “se aspetti
10
Risposta: risulterebbe limx→x0 f (x) = l per ogni l ∈ R! Quindi la definizione
non sarebbe ben posta.
LIMITI DI FUNZIONI
9
x > 1500 sarà come vuoi |f (x) − 1| < 3 · 10−6 , ma non è detto che non lo sia anche
prima” (per esempio potrebbe essere |f (x) − 1| < 3 · 10−6 ⇔ x > 1100); la doppia
freccia dice “per x > 1500, e non prima, risulta |f (x) − 1| < 3 · 10−6 ”. In generale
non si ottiene la doppia freccia; è già abbastanza ottenere qualche δǫ , anche se non
il migliore possibile.
I seguenti esempi sono tutti “Studia l’approssimazione del limite . . . ”, nel senso
di: “Dato ǫ trova un δǫ (o xǫ , o quello che è a seconda dei casi) tale che . . . ”,
eccetera. Il primo dà un’idea sul tipo di problema e su due tipiche direzioni in
cui muoversi, vediamolo un momento: è limx→∞ f (x) = 0, dunque si vuole xǫ tale
che x > xǫ ⇒ |f (x)| < ǫ; più piccolo è xǫ meglio è. Uno, si può vedere è se
per qualche xǫ l’implicazione voluta è ovviamente vera —primo passo di (a) qui
sotto. Due, si può cercare una funzione
g con
√
√ |f | < |g| che
√ tende pure a zero e di
cui la |g| < ǫ è facile; in (a) f = x + 1 − x, g = 1/2 x, ed è immediato che
|g| = g < ǫ ⇔ x > 1/4ǫ2; per tali valori sarà certamente |f | < ǫ; ma è chiaro anche
che non abbiamo trovato il miglior xǫ possibile —disegna per x ≥ 0: una retta
orizzontale ad altezza ǫ < 1, f che scende convessa da 1 a zero, e g tutta sopra f
convessa decrescente da ∞ a zero; l’xǫ = 1/4ǫ2 trovato è il punto in cui g incontra
la retta ǫ, ma il migliore possibile è quello in cui f inontra ǫ, che è più indietro.
√
√
11
ESEMPI. (a) Considera
(
Qui
√ limx→∞
√ x + 1 − x) = 0, e supponi ǫ < 1.
|f (x)| = f (x) p
= 1/( x + 1 + x), sicchè con qualche passaggio facile troviamo
|f (x)| < ǫ ⇔ 2 x(x + 1) > ǫ−2 − 1 − 2x. Un primo risultato è allora immediato:
se il secondo membro di questa è negativo la disequazione è soddisfatta, cioè: x >
(1 − ǫ2 )/2ǫ2 ≡ xǫ ⇒ |f (x)| < ǫ. Facile ma scarso; nell’esempio (g) di pagina 3
avevamo già trovato di meglio, con x′ǫ = 1/4ǫ2 ≈ xǫ /2 per ǫ sufficientemente piccolo.
Se vogliamo il più piccolopx tale che x > x ⇒ |f (x)| < ǫ, prendiamo x ≤ xǫ ed
eleviamo al quadrato la 2 x(x + 1) > ǫ−2 − 1 − 2x (che con x ≤ xǫ ha entrambi i
membri positivi); otteniamo l’equivalente x > (1 − ǫ2 )2 /4ǫ2 ≡ x′′ǫ < x′ǫ , che a questo
punto è anche equivalente a |f (x)| < ǫ. Più di questo non si può fare.
(b) limx→∞ (1 − x1 + x12 ) = 1. Prendiamo x > 1; per tali valori, |f (x) − 1| <
ǫ ⇔ ǫx2 −√x + 1 > 0; quest’ultima relazione vale per ogni x se ǫ > 1/4, e per
x > (1 + 1 − 4ǫ)/2ǫ altrimenti (le x < . . . non ci interessano mentre x → ∞).
Conclusione:
|f (x)−1|
√ < ǫ vale per x > 1 ≡ xǫ se ǫ > 1/4; vale per
√ x > max{1, (1+
√
1 − 4ǫ)/2ǫ} = (1 + 1 − 4ǫ)/2ǫ ≡ xǫ altrimenti (vero che (1 + 1 − 4ǫ)/2ǫ > 1?).
Qui non abbiamo trovato la doppia implicazione.
x
1
(c) limx→∞ 1+|x|
= 1. Prendi x ≥ 0; per tali valori |f (x) − 1| < ǫ ⇔ 1+x
<ǫ⇔
−1
−1
x > ǫ − 1; sicchè x > max{0, ǫ − 1} ≡ xǫ ⇒ |f (x) − 1| < ǫ. Se si analizza anche
x < 0 ci si rende presto conto che qui siamo arrivati.
q
(d) Sia x < −3, e considera limx→−3− x−4
x+3 = ∞. Vogliamo δK tale che per
−3 − δK < x < −3 risulti f (x) > K, e supponiamo K > 1. x < −3 garantisce
che sotto radice c’è un numero positivo, e K > 1 che la divisione per K 2 − 1
2
2
2
preserva il verso, quindi: f (x) > K ⇔ x−4
x+3 > K ⇔ x(K − 1) + (4 + 3K ) > 0 ⇔
2
7
7
+4
x > − 3K
K 2 −1 = −3 − K 2 −1 ; allora possiamo prendere δK = K 2 −1 . In questo caso
abbiamo trovato la migliore approssimazione possibile.
x−1
= 2, ed ǫ < 1. Risolvendo troviamo (dopo un pò di
(e) Considera limx→3 x−2
lavoro) |f (x) − 2| < ǫ ⇔
11
|x−3|
|x−2|
< ǫ ⇔ x ∈ (3 −
ǫ
1+ǫ , 3
+
ǫ
1−ǫ );
quindi con δǫ =
Come già osservato in precedenza, per quanto riguarda la validità della relazione di limite basta prendere ǫ < ǫ arbitrario; l’analisi dell’approssimazione
potrebbe essere condotta anche, indipendentemente, per ǫ ≥ ǫ. Lo stesso dicasi
per K > K.
LIMITI DI FUNZIONI
10
ǫ
ǫ
ǫ
min{ 1+ǫ
, 1−ǫ
} = 1+ǫ
si ha |x − 3| < δǫ ⇒ |f (x) − 2| < ǫ, e non esiste δǫ′ > δǫ per
il quale questa implicazione resta vera: anche qui l’approssimazione trovata è la
migliore possibile.
|x−3|
<
Un risultato più debole si trova più speditamente come segue. Vogliamo |x−2|
|x−3|
ǫ; ma |x − 3| < 1/2 implica |x − 2| > 1/2 e dunque |x−2|
< 2|x − 3| (in questo
caso vicino ad x = 3 abbiamo trovato |f (x) − l| < |g| con g → 0 facile); sicchè
|x − 3| < min{1/2, ǫ/2} = ǫ/2 ≡ ϑ ⇒ |f (x) − 2| < ǫ. Nota che per tutti gli ǫ < 1
ǫ
(giusto?).
(quelli che stiamo prendendo in considerazione) è ϑ < 1+ǫ
(f ) limx→1
√
x−1
x−1
=
1
2
(x > 0, x 6= 1; f (x) =
√ 1 ).
x+1
Consideriamo ǫ < 1/2. Risol√
1− √x
vendo le disequazioni irrazionali che vengono fuori si trova |f (x) − 21 | = | 2(1+
|<
x)
1+2ǫ 2
1−2ǫ 2
d
s
d
s
ǫ ⇔ x ∈ (1 − δǫ , 1 + δǫ ) con δǫ = 1 − 1+2ǫ , δǫ = 1−2ǫ − 1; dunque il miglior
risultato ottenibile è δǫ = min{δǫs , δǫd }.
|x−1|
√ 2 < |x − 1| (perchè il denominatore è > 1),
Più facile: |f (x) − 1/2| = 2(1+
x)
quindi con ϑǫ = ǫ vale la |x − 1| < ϑǫ ⇒ |f (x) − 1/2| < ǫ. Più facile, ma ϑǫ < δǫ
(qui casca l’asino). Per verificare questo si risolvano brutalmente (non è difficile
come sembra) le disequazioni ǫ < δǫs ed ǫ < δǫd e si constati che entrambe sono vere
per tutti gli ǫ < 1/2 (quelli in esame).
ESERCIZI
1. Verifica che ∀c ∈ R si ha limx→x0 c = c.
2. Verifica (assumendo che il codominio di cos x è un intervallo) che
limx→ 1− arccos x = 0.
3. Dimostra che se limx→∞ f (x) = ∞ anche limx→∞ (y0 + f (x − x0 )) =
∞; lo stesso per f → −∞ e per x → −∞ (qui il primo passo dell’esercizio
è scrivere i risultati cui si accenna!)
4. Verifica che: se limx→∞ f (x) = l, limx→∞ (y0 + f (x − x0 )) = l + y0 ;
e che lo stesso vale con −∞ al posto di ∞.
5. Dimostra che limx→−x+0 f (−x) = limx→x−0 f (x) (disegna prima).
6. Un teorema dei carabinieri: se per x > x1 f (x) ≥ g(x) e limx→∞ g(x) =
∞, anche limx→∞ f (x) = ∞. Qual è l’analogo enunciato per x → x0 ?
7. Scrivi un paio di casi di negazione della frase limx→x0 f (x) = l. In
nota x0 , l ∈ R ed x0 ∈ R, l = ∞. 12
12Primo
caso: esiste ǫ > 0 tale che per ogni δ > 0 esiste x con 0 < |x − x0 | < δ
tale che |f (x) − l| ≥ ǫ. Secondo: esiste K tale che per ogni δ > 0 esiste x con
0 < |x − x0 | < δ tale che f (x) ≤ K.
LIMITI DI FUNZIONI
11
8. ‘Verifiche’ (vedi paragrafo ‘Approssimazione al Limite’):
√
√
(i) lim x( x + 1 − x) = ∞
x→∞
x
= −∞
x→1 1 − x
x+2
(v) lim
=4
x→2 x − 1
(iii) lim+
x
= −1
x→−∞ 1 + |x|
x−2
(iv) lim
= −∞
x→0 x2
1
2x + 1
(vi) lim
=
x→0 x + 2
2
(ii) lim
RISULTATI SUI LIMITI: I
Il risultato che ora stabiliremo consente di trasferire alle funzioni i
risultati già dimostrati sui limiti delle successioni, ed altro.
Siano x0 , l ∈ R ∪ {±∞}, ed (xn ) una successione con
xn ∈ Df ∀n. E’ limx→x0 f (x) = l se e solo se:
PROPOSIZIONE.
xn 6= x0 ed xn → x0 ⇒ f (xn ) → l.
(∗)
Dim. Facciamo x0 , l ∈ R. Se limx→x0 f (x) = l, è |f (x) − l| < ǫ se
0 < |x − x0 | < δǫ ; ma definitivamente è 0 < |xn − x0 | < δǫ (per
ipotesi), dunque anche |f (xn ) − l| < ǫ. Il viceversa per contraddizione:
supponiamo che non sia limx→x0 f (x) = l. Allora c’è un ǫ0 > 0 tale che
in ogni intorno di x0 esiste x 6= x0 con f (x) 6∈ (l − ǫ0 , l + ǫ0 ). Prendendo
intorni di raggio 1, 1/2, . . . , 1/n . . . abbiamo allora: per ogni n esiste
xn con 0 < |xn − x0 | < 1/n ed |f (xn ) − l| ≥ ǫ0 . La successione di questi
xn falsifica l’ipotesi (∗), perchè x0 6= xn → x0 ma f (xn ) 6→ l.
Nota che la condizione xn 6= x0 (basta definitivamente) è necessaria:
per esempio se limx→x0 f (x) = l 6= f (x0 ), la successione definita da
xn = x0 ∀n converge ad x0 , ma f (xn ) → f (x0 ) 6= l.
I risultati seguenti contengono in realtà tutto ciò che la teoria offre
sui limiti. Per il loro calcolo potremo usare questi, più la conoscenza
di due limiti veramente ‘notevoli’ ai quali molti altri possono essere
ricondotti.
(a) I risultati su somma e prodotto di limiti (cioè, va
sempre come ci si aspetta tranne nei casi ∞ − ∞ e 0 · ∞). Esempio,
se limx→x0 f (x) = l e limx→x0 g(x) = m, allora limx→x0 (f (x) + g(x)) =
l + m (qui x0 , l, m ∈ R ∪ {±∞}). Perchè: scriviamo s(x) = f (x) + g(x);
applicando la proposizione di sopra (parte ‘solo se’) ad f e g, se x0 6=
xn → x0 risulta f (xn ) → l e g(xn ) → m; allora (somma di limiti di
successioni) s(xn ) = f (xn ) + g(xn) → l + m; applicando la proposizione
(parte ‘se’) ad s si ottiene allora il risultato.
Nota in particolare che somma e prodotto di funzioni continue in x0
sono continue in x0 .
CONSEGUENZE.
LIMITI DI FUNZIONI
12
E’ essenziale a questo punto fare anche la dimostrazione diretta di
qualche caso di somma e prodotto. In nota ci sono, per controllare, la
somma l + ∞ con x0 = ∞ e il prodotto lm con x0 , l, m ∈ R. 13
(b) Limiti delle funzioni elementari : esponenziali x 7→ ax e loro inverse x 7→ loga x, potenze x 7→ xα , e trigonometriche vanno come
ci si aspetta. Per esempio, possiamo affermare che per x0 ∈ R è
limx→x0 ax = ax0 , infatti: abbiamo dimostrato che per ogni sequenza
(xn ) con limite x0 risulta axn → ax0 ; applicando la proposizione di sopra si ottiene il risultato. Analogamente si vede che per esempio per
x0 = −∞ si ha limx→x0 ax = 0.
Di nuovo nota la continuità: tutte le funzioni fondamentali sono
continue sui rispettivi domini.
(c) I limiti dell’esempio precedente anche se al posto di x mettiamo
f (x). Esempio, se f (x) > 0 e limx→x0 f (x) = 0 (x0 ∈ R∪{±∞}), allora
limx→x0 log f (x) = −∞. Perchè se x0 6= xn → x0 risulta (ipotesi più
‘solo se’ qui sopra) 0 < f (xn ) → 0; ma per tale successione sappiamo
che log f (xn ) → −∞; risultato dal ‘se’ della proposizione. Esercizio, se
limx→x0 f (x) = −∞ allora limx→x0 af (x) = 0.
(d) Limiti di f g : per f (x) > 0, il limx→x0 f (x)g(x) , per x0 ∈ R ∪ {±∞},
va sempre come ci si aspetta —il che si vede scrivendo f (x)g(x) =
eg(x) log f (x) — eccetto quando ad esponente (di e) si trova un 0 · ∞
(o ∞ · 0). Esempio, se limx→∞ f (x) = 0 e limx→∞ g(x) = ∞ allora
limx→∞ f (x)g(x) = 0. Dimostrazione: da (c) segue limx→∞ log f (x) =
−∞; dunque (da (a)) limx→∞ g(x) log f (x) = −∞, da cui (usando (c)
di nuovo) limx→∞ eg(x) log f (x) = 0.
In altre parole: se f → l e g → m, l, m ∈ R abbiamo f g → lm , e
analogo passaggio al limite si può fare se l, m non sono finiti purchè
g log f non sia 0 · ∞ o ∞ · 0. Quando si verificano gli ultimi due casi?
Il primo è con m = 0 e log f → ±∞, che si verifica se f → 0 oppure
f → ∞; il secondo è con m = ±∞ e log f → 0, cioè l = 1; dunque i
casi scoperti (indeterminati) sono: “00 , ∞0 , 1±∞ ”.
(e) Per x → ∞, ax (a > 1) va a infinito “più veloce di” qualunque
potenza di x:
Per a > 1,
13Somma:
ax
= ∞ ∀k ∈ N+ .
x→∞ xk
lim
l’ipotesi è che limx→∞ f = l, limx→∞ g = ∞. Sia K arbitrario;
esistono x1 , x2 tali che f > l − 1 per x > x1 e g > K − (l − 1) per x > x2 ; per
x > max{x1 , x2 } = xK sarà allora f + g > K.
Prodotto: l’ipotesi è che limx→x0 f (x) = l, limx→x0 g(x) = m. Allora dato ǫ:
per x ∈ I1 \ {x0 }, |g(x) − m| < ǫ/2l, da cui anche |g(x)| < |m| + ǫ/2l ≡ M ; per
x ∈ I2 \ {x0 }, |f (x) − l| < ǫ/2M ; dunque per x ∈ I1 ∩ I2 \ {x0 }, |f g − lm| =
|f g − lg + lg − lm| ≤ |g| · |f − l| + l|g − m| < ǫ.
LIMITI DI FUNZIONI
13
Nota che dicendo f va a infinito ‘più veloce’ di g intendiamo che il
rapporto f /g va a infinito, cioè che f diventa infinitamente più grande
di g; per esempio 2x non va più veloce di x, perchè il rapporto è sempre
2; x2 invece sı̀. Per verificare il limite, anche qui non dobbiamo fare
altro che applicare il risultato sulle successioni, che se xn → ∞ allora
axn /xkn → ∞, e poi il ‘se’ della proposizione qui sopra.
Più in generale, se limx→x0 f (x) = ∞ allora limx→x0 af (x) /f (x)k = ∞,
perchè: da limx→x0 f (x) = ∞ e ‘solo se’ di sopra deduciamo che
per xn → x0 si ha f (xn ) → ∞, da cui (risultato sulle successioni)
af (xn ) /f (xn )k → ∞; ora il risultato voluto segue dal ‘se’ della proposizione di sopra.
(f) Per x → ∞ il logaritmo va a infinito “più lento” di tutte le potenze
di x: 14
loga x
Per a > 1, lim (1/k)
= 0 ∀k ∈ N+ .
x→∞ x
Ponendo h(x) = loga x abbiamo limx→∞ h(x) = ∞ e loga x/x(1/k) =
h(x)/(a1/k )h(x) ; ed a1/k > 1 poichè a > 1; dall’esempio precedente
(prendendo l’inverso) segue allora il risultato.
Da (e) ed (f) viene fuori questo quadro: per x → ∞, il log è più lento
di tutte le xα con α > 0, queste vanno più veloci quanto maggiore è α,
e tutte sono più lente di ax (con a > 1).
ESEMPI ED ESERCIZI: I
Cominciamo adesso a vedere questi risultati ‘in azione’ nel calcolo di
limiti che si trovano per continuità, con razionalizzazioni, dividendo
numeratore e denominatore per uno stesso numero, aggiungendo e
togliendo qualcosa, usando formule per an − bn e cose simili. La cosa
notevole è che molti altri limiti si trovano riconducendoli a due limiti
particolari (‘notevoli’ appunto). Devi, specialmente all’inizio, accertarti di sapere quale risultato si sta usando in ogni passaggio.
(a) Studiamo limx→±∞ an xn +an−1 xn−1 +. . .+a1 x+a0 al variare
di n ed an . L’idea è che xn diventa infinitamente più grande di tutti
gli altri termini, quindi ‘conta solo lui’; per farlo uscire lo mettiamo in
evidenza, ottenendo f = xn · (an + an−1 /x + . . . + a1 /xn−1 + a0 /xn );
la funzione in parentesi tende ad an 6= 0, ed xn → ±∞ (a seconda se
x → ±∞ e se n è pari o dispari); dunque prodotto di limiti (in R),
risultato ∞ o −∞ (per esempio se x → −∞, an < 0 ed n è pari risulta
limx→∞ f = −∞, ecc.).
Da somma limiti sappiamo che per x0 ∈ R, per ogni polinomio P (x)
risulta limx→x0 P (x) = P (x0 ), che cioè i polinomi sono funzioni continue
su tutto R (giusto?).
ESEMPI.
14Qui
e nel precedente diciamo ‘tutte’ le potenze, ma i risultati contemplano solo
k e 1/k, k ∈ N+ ; estendili con maggiorazioni a esponenti arbitrari.
LIMITI DI FUNZIONI
14
√
x+1
(b) limx→∞ log √
. Basta vedere che fa la frazione (conseguenza
3
2 x+1
(c)): in evidenza sopra x1/2 e sotto x1/3 , resta x1/6 moltiplicato una
frazione che tende a 1/2; dunque la frazione tende a infinito, e con essa
il suo logaritmo.
3
x −4x
3
4
(c) limx→−∞ −x
4 +2 . In evidenza quello che conta, x sopra e x sotto,
2
1−4/x
→ 0 · (−1) = 0 (stiamo usando la freccia, è chiaro
resta f = x1 −1+2/x
4
che si intende “per x → −∞”).
1
. Il denominatore è un polinomio che
(d) limx→−1 3
2
2x + 2x − 3x − 3
si annulla in x = −1, e possiamo usare il seguente fatto:
Sia P (x0 ) = 0, con P (x) = an xn + an−1 xn−1 + . . . + a1 x + a0 ; allora
P (x) = (x − x0 )Q(x) con Q polinomio di grado n − 1. 15
Dividendo il nostro denominatore per x + 1 otteniamo 2x3 + 2x2 −
3x − 3 = (x + 1)(2x2 − 3); limx→−1(2x2 − 3) = −1 < 0, dunque:
limx→−1∓ f (x) = ±∞ (terzo esercizio qui sotto), sicchè il limite per
x → −1 non esiste. C’è un ‘asintoto verticale’, e quando il numeratore
non tende a zero e il denominatore è un polinomio che tende a zero ce
lo aspettiamo sempre.
4
(e) limx→0 xx+4x
2 −2x3 . Qui numeratore e denominatore tendono entrambi
a zero. Mettiamo in evidenza x elevato all’esponente minimo sopra e
sotto, ottenendo 1/x per una frazione che tende ad 1; conclusione, il
limite non esiste.
1
3
3
(f) limx→1 1−x
− 1−x
= (1 − x)(1 + x + x2 ))
3 . Qui (usando 1 − x
troviamo f (x) =
x2 +x−2
1−x3
=
(x−1)(x+2)
(1−x)(1+x+x2 )
(x+2)
= − 1+x+x
2 → −1.
(g) limx→−∞ x5 (2 sen x + cos x − 5). La funzione in parentesi forse non
ha limite, ma è sempre < −2 < 0; inoltre, esiste x0 tale che per x < x0
risulta x5 < −K/2; dunque per tali x è f (x) > K, e il limite è ∞.
2
(h) limx→0+ (x + x2 )1/x . Scrivendolo come eg·log f si vede subito che
l’esponente tende a ∞ · (−∞) = −∞, quindi il limite vale 0.
1−sen 2x
(i) limx→ π4 sen
. Moltiplica e dividi sopra per 1 + sen 2x e sotto
x−cos x
2
x+cos x
· −coscos2x
→ 0.
per sen x + cos x, ottenendo f (x) = sen1+sen
x
2x
(j) limx→0 sen x1 ·log(x+1). Funzione limitata moltiplicata per funzione
infinitesima: limite 0.
√
2
√
2
x +2x−6
(k) limx→3 x −2x+6−
. A numeratore a−b, ed a2 −b2 = −4(x−
x2 −4x+3
3); a denominatore c’è (x − 1)(x − 3); conclusione, −1/3.
15Dim.
Per x 6= x0 , la divisione P (x)/(x − x0 ) dà P (x) = (x − x0 )Q(x) + r con
r ∈ R. Facendo i limiti per x → x0 di entrambi i membri si ottiene P (x0 ) = r.
LIMITI DI FUNZIONI
15
(l) Anche le inverse delle funzioni circolari (arcsen, arccos, arctan) sono
continue sui rispettivi domini. Anche questo non siamo ancora in grado
di dimostrarlo rigorosamente, ma siccome lo vogliamo usare vediamo
almeno una ‘giustificazione’ del risultato: facciamo limx→x0 arctan x =
arctan x0 . Sia dato ǫ > 0, e sia y0 = arctan x0 (nota tan y0 = x0 );
poichè arctan x è crescente, per x ∈ (tan(y0 − ǫ), tan(y0 + ǫ)) è y0 − ǫ <
arctan x < y0 + ǫ; dunque basta prendere δǫ = min{x0 − tan(y0 −
ǫ), tan(y0 + ǫ) − x0 }. 16
A questo punto puoi fare gli esempi 4.9 del libro.
ESERCIZI 4.1
Aggiungiamo un paio di esercizi di teoria e altri limiti.
9. Ricorda che una successione convergente è limitata. Ora supponi che
∃ limx→∞ f (x) = l ∈ R. E’ f necessariamente limitata? No; disegna
un controesempio. Cosa secondo te fa la differenza?
10. Dimostra la Proposizione 4.6 (p.198).
1
11. (i) Dimostra che limx→x0 f (x) = −∞ implica limx→x0 f (x)
= 0.
(ii) Supponi che limx→x0 f (x) = 0; dimostra che se f (x) > 0 allora
1
1
limx→x0 f (x)
= ∞, e che se f (x) < 0 allora limx→x0 f (x)
= −∞
12. Calcola limx→±∞
tutti).
x5 −3x+1
x2 +x+2
(di questi quando se ne fa uno si sono fatti
13. Dı̀ se esistono limx→1
x−5
(x−1)(x−3)
14. Dı̀ se esistono limx→0
x3
x2 −2x
2
x −1
e limx→2 x3 −4x
2 +4x .
5
3
−x
e limx→0 xx4 −3x
.
15. Calcola, se esiste:
x3 + 1
(i) lim 2
x→−1 x + 1
ex
(iii) lim x
x→∞ e − 1
[x]
(v) lim
x→∞ x
x − tan 2x
(vii) lim
π + x − tan x
x→ 4
16Di
√
x2 + x
x→−∞ 2x + 1
(x + h)3 − x3
(iv) lim
h→0
h
sen x + 3 cos x
(vi) lim
x→−∞
x − cos x
x
e − e−x
(viii) lim x
x→∞ e + e−x
(ii) lim
nuovo, il ‘buco’ in questa argomentazione è che abbiamo dato per scontato
che il codominio della tangente è un intervallo (se no come potremmo essere sicuri
che ogni x ∈ (tan(y0 − ǫ), tan(y0 + ǫ)) è nel dominio di arctan x? Disegna l’inversa
di una funzione monotona ma non continua in x0 per capire qual è il problema).
Dimostreremo che il codominio di qualunque funzione continua (come la tangente)
è un intervallo.
LIMITI DI FUNZIONI
√
x−1
(ix) lim √
3
x→1
x−1
√
3
(xi) lim x + 1 − x3
x→∞
(xiii) lim x2 arctan x
x→−∞
16
√
3 − 5x − 1
(x) lim
x→2
x2 − 4
√
(xii) lim x + x2 + 4x + 3
x→−∞
(xiv) lim−
x→1
1
arccos x
1 + arctan x
(xv) lim
x→−∞ π + 2 arctan x
√
Suggerimenti. (ii) ricorda che per x < 0 è x = −x; (v) usa carabinieri; (ix) ricorda a2 −b2 = (a−b)(a+b), a3 −b3 = (a−b)(a2 +ab+b2 );
(xi) a3 + b3 = (a + b)(a2 − ab + b2 ); (xii) vedi (ii); (xiv) ricorda (esercizio
2 pag.10) che limx→1− arccos x = 0, e concludi dal segno di arccos x.
16. Questi sono f g :
x2 + 2 x2
x→±∞ 2x2 + 1
√ 1
(iii) lim− (1 − x) x−1
(i) lim
x→1
(ii) lim+ (1 − cos x)1−ln x
x→0
(iv) lim esen x/x
x→−∞
(vi) lim+ x1/x
ln x
(v) lim+ x
x→0
x→0
(vii) lim− (cos x)
tan x
x→ π2
x+1
sulla base dei limiti per x →
17. Fatti un’idea del grafico di x2 −4x+3
x2 −1
1, 3, ±∞; e di quello di x3 −4x2 +4x dai limiti per x → 0, 2, ±∞.
18. (Barozzi-Corradi) Discuti al variare di a (maggiore di zero diverso
a (x−a)
da 1) il limite limx→a+ log
log x−1
a
RISULTATI SUI LIMITI: II
La seguente proposizione regola il ‘cambio di variabile’, che nei limiti
è (quasi) tutto. Dice: se per x vicino ad x0 è g(x) vicino a z0 e per z
vicino a z0 è f vicino ad l, allora per x vicino ad x0 sarà f vicino ad l.
Con I(ξ) (o J(ξ)) indicheremo un intorno di ξ (cioè un (ξ − δ, ξ + δ) se
ξ ∈ R, (a, ∞) se ξ = ∞, (−∞, a) se ξ = −∞).
PROPOSIZIONE (Limiti
Funzioni Composte, LFC). Siano x0 , z0 reali
o ±∞. Se limx→x0 g(x) = z0 ed esiste limz→z0 f (z) ∈ R, allora
lim f (g(x)) = lim f (z)
x→x0
z→z0
purchè si verifichi almeno una delle seguenti condizioni:
(1) limz→z0 f (z) = f (z0 );
(2) esiste I(x0 ) tale che per ogni x ∈ I(x0 ) \ {x0 } si ha g(x) 6= z0 .
Dim. Usiamo la condizione 2, a te l’altra. Sia l = limz→z0 f (z), e sia
dato un intorno J(l) di l; le ipotesi implicano che esiste I(z0 ) tale che
LIMITI DI FUNZIONI
17
per z ∈ I(z0 ) \ {z0 } è f (z) ∈ J(l), ed un I(x0 ) tale che per x ∈ I(x0 ) \
{x0 } è g(x) ∈ I(z0 ) \ {z0 }; per tali x sarà allora f (g(x)) ∈ J(l).
Nota. La condizione (ii) è automaticamente verificata se z0 = ±∞;
altrimenti, una condizione sufficiente spesso facile da vedere è che z =
g(x) sia strettamente monotona in un I(x0 ) \ {x0 }.
I limiti notevoli sono i due seguenti:
sen x
(i) lim
=1
x→0
x
(ii)
lim
x→±∞
1 x
1+
= e.
x
1 − cos x
1
Il primo ha per compagno limx→0
=
che si ottiene da (i)
x2
2
moltiplicando e dividendo per 1 + cos x. Il secondo può riscriversi
cambiando variabili come:
ln(1 + x)
=1
x→0
x
(iia) lim
ex − 1
=1
x→0
x
(iib) lim
((iia): con z = 1/x → ±∞ la funzione è il ln di quella in (ii); poi usa
LFC. (iib): prendi z = ex − 1 → 0 e usa (iia)).
Per verificare (i) e (ii) non resta molto lavoro. Una verifica di (i)
è: prendi 0 < |x| < π2 , cosı̀ | sen x| < |x| < | tan x|; e dividi per
| sen x| racchiudendo x/ sen x fra due funzioni che tendono ad 1. Per
(ii), cominciando da x → ∞ osserva che ([x] parte intera di x)
1 [x] 1 x 1 [x]+1
1+
< 1+
< 1+
[x] + 1
x
[x]
e che le due funzioni che chiudono f tendono entrambe ad e (per x →
∞, [x] descrive N, [x] = 1, 2 . . .). Per x → −∞, con z = −x → ∞
scrivi
1 x 1 −z z z 1 z
1+
= 1−
=
= 1+
,
x
z
z−1
z−1
che tende ad e.
ESEMPI ED ESERCIZI: II
Qualche consiglio, perchè i vecchi non possono fare a meno di darne.
Primo ricordati degli amici: f + g, f · g ed f g = eg log f vanno come
vuoi, se non ci sono ∞ − ∞ o 0 · ∞; f ◦ g con f fondamentale non
tradisce mai; e se arrivi a un limite notevole sei a casa. Poi, pronto
a riscrivere la funzione data: levando ‘problemi’ con moltiplicazioni
e divisioni, aggiungendo e togliendo, prendendo archi complementari
nelle trigonometriche, eccetera, sperando che il prezzo da pagare sia
basso; e/o cercando la variabile ‘giusta’ (che spesso risolve). Infine, a
volte non resta che tentare uno ‘schiacciamento’ (carabinieri).
LIMITI DI FUNZIONI
18
x
. Moltiplica e dividi sopra per x2 , sotto per
(a) limx→0 1−cos
sen x
x; resta x per una frazione che tende a 1/2, dunque il limite vale 0.
x
(b) limx→±∞ 1 + αx . Dentro parentesi vogliamo “1 su. . . ”, quindi
scriviamo α/x = 1/(x/α); chiaramente la variabile da considerare è
adesso z = x/α → ±∞ (con direzione opposta ad x se α < 0); ad
esponente vogliamo allora z, e lo otteniamo moltiplicando
e dividendo
z α
α
per α; dunque limx→±∞ f (x) = limz→±∞ (1 + 1/z)
= e , usando la
conseguenza (c) di sopra.
ln x
(c) limx→1
. sotto c’è z = x − 1 → 0, e sopra 1 + z; sappiamo
x−1
allora dal limite notevole (iia) che anche il nostro vale 1. Questo, e
possibilmente anche il prossimo, non è male ricordarlo.
(1 + x)α − 1
(d) limx→0
. Usiamo l’esempio precedente: sopra abbiamo
x
uno z − 1 con z = (1 + x)α → 1; se sotto ci fosse log z saremmo a casa,
e ce lo mettiamo, ‘pagando’ una moltiplicazione per log(1 + x)α =
α log(1 + x), che però resta diviso per x col quale va ad 1; risultato:
z−1
· limx→0 log(1+x)
= α.
limx→0 f (x) = α · limz→1 log
z
x
ESEMPI.
(e) limx→0+ x log x. Questo è importante. f (x) = − log(1/x)
, e z =
1/x
log z
1/x → ∞; dunque limx→0+ f (x) = − limz→∞ z = 0.
Analogamente si vede che per ogni α > 0 è limx→0+ xα log x = 0.
√
(f) limx→∞ log x− 12 log x. Prendi z = log x → ∞, trovando limx→∞ f =
√
√
limz→∞ z − 12 z = −∞ (mettendo in evidenza z).
tan x
1
sen x
= limx→0
·
= 1.
x
cos x
x
arcsen x
(h) limx→0
. Per x → 0, z = arcsen x → 0 monotona, ed
x
x = sen z; da LFC limx→0 f (x) = limz→0 z/ sen z = 1.
(g) limx→0
(i) limx→1 (1 − x) tan π2 x. Per x → 1, sen π2 x → 1 senza problemi; e
cos α = sen(π/2 − α), dunque cos π2 x = sen(π/2 − π2 x) = sen(1 − x) π2 ;
allora prendiamo z = (1 − x) π2 → 0, e moltiplicando e dividendo per π2
otteniamo limx→1 f (x) = 2/π.
(j) limx→− π − (x + π2 ) tan x. Prendi z = x + π2 → 0− e osserva che
2
tan x = −1/ tan(x + π2 ), cosı̀ limx→− π − f = − limz→0− z/ tan z = −1.
2
sen x−cos x
.
sen 4x
(k) lim
sen 4x = 2 sen 2x cos 2x, e il problema è cos 2x;
ma questo lo otteniamo, cambiato di segno, al numeratore moltiplicando e dividendo √
per sen x + cos x; dopo le semplificazioni il limite è
facile, e vale −1/2 2.
x→ π4
(l) (Di Bari–Vetro) limx→0+ log x · log(1 + x3 ). Moltiplica e dividi per
x3 e applica l’esempio (e): il limite è 0.
LIMITI DI FUNZIONI
19
(m) (Picone–Fichera) limx→0 sen x1 · log x + senx x . Funzione limitata
per funzione infinitesima: limite 0.
1 − senx x
(n) limx→0
. Qui moltiplicando ecc. non si arriva a niente, ma
x
ciò non può sorprendere perchè stiamo cercando di andare più a fondo
su sen x/x; che tende ad uno va bene, ma qui ci stiamo chiedendo
a che velocità: 1 − sen x/x va a zero più veloce di x, uguale, o più
lento? Dobbiamo usare confronto. Prendiamo 0 < |x| < π/2, cosı̀
è 1 < senx x < cos1 x ; da questo ricaviamo 0 < 1 − senx x < 1 − cos x;
moltiplicando per 1/|x| = |x|/x2 viene
1
sen
x
< |x| · 1 − cos x ;
0 < · 1 −
x
x x2
la funzione a destra tende a zero, e in mezzo c’è |f |: possiamo concludere che il limite vale zero. Dunque per x → 0, 1 − sen x/x diventa
infinitamente più piccolo di x, cioè va a zero più veloce.
ESERCIZI 4.2
Al solito aggiungiamo qualche limite.
1. Questi con il primo limite notevole.
x + sen x
(i) lim+ √
x→0
1 − cos x
tan x − sen x
(iii) lim
x→0
x3
x2
(v) lim
x→0 1 − cos αx
1
1
(vii) lim
−
x→0 sen x
tan x
sen(α + x) − sen(α − x)
(ix) lim
x→0
x
π
(x − ) tan x
(xi) lim
2
x→ π2 +
2. Questi con il secondo.
x − 1 x
(i) lim
x→±∞ x + 1
1
(iii) lim x(a x − 1)
x→∞
ex − e2x
x→0 sen x − sen 2x
√
e x−1 − 1
(vii) lim+
x→1
x−1
(v) lim
x + sen x
(ii) lim− √
x→0
1 − cos x
1
(iv) lim x sen
x→∞
x
arctan x
(vi) lim
x→0
x
√
1 − cos x
(viii) lim−
x→0
x
sen πx
(x) lim
x→1 (x − 1)3
sen x
ex − 1
(iv) lim (1 + sen x)1/x
x→0
x − 1 x+2
(vi) lim
x→∞ x + 3
(ii) lim
x→0
(viii) lim (1 + x)1/x
x→0
LIMITI DI FUNZIONI
(ix) lim x(ln(x + 1) − ln x)
(1 + sen x)2 − 1
x→0
x
3. Altri misti, da calcolare se esistono.
(i) lim [cos x]
x→0
√
sen x + 4 1 + x − 1
(iii) lim
x→0
x + arctan x
cos x − cos 2x
(v) lim
x→0
1 − cos x
ln(3x2 + 2)
x→∞
x
1
(ix) lim x sen(π − )
x→∞
x
5x
(xi) lim 4
x→∞ x − 3x3 + 2x − 1
(vii) lim
ex − e2x
x→0
x
(x + h)α − xα
(xii) lim
h→0
h
(x) lim
x→∞
(xi) lim
20
π
− x)
x→0
2
sen(sen x)
lim
x→0
x
√
ln(1 + x − 1)
√
lim
x→1+
x2 − 1
r
1
1+x
lim ln
x→0 x
1−x
(x + 1)x ln x + (3x − 1) tan x
lim+
x→0
arctan x − x sen x
sen x + arctan x
lim
x→0 ln(1 + x) + 3x − 1
(ii) lim x2 tan4 (
(iv)
(vi)
(viii)
(x)
(xii)
√
√
2
(xiii) lim x + (x − [x])2
(xiv) lim e x − e x −1
x→0
x→∞
r
1
1 + x2
x2
(xv) lim−
arctan
x
(xvi)
lim
(cos
x)
x→0
x→0
x2
1−cos x
− 12
1
1
x2
(xviii) lim
(xvii) lim −
x→0
x→0 x
sen x
x
α
α
α
Per l’(viii) ricorda (x/y) = x /y . Nel (xiii) fai separatamente da
destra e sinistra. Nel (xvi) nota che 1 − cos x → 0. Per gli ultimi due
usa il risultato dell’ultimo esempio sopra. Valori dei limiti in nota. 17
4. Altri due, con suggerimento di guardare fra gli esercizi di ‘Geometria’
(soluzioni in nota 18)
x
x
(ii) lim−
(i) lim+
π
π
1
1
x→0 x + arctan +
x→0 x + arctan −
x
2
x
2
√
0; (ii) ∞; (iii) 5/8, dividendo per x; (iv) 1; (v) 3; (vi) 1/ 2; (vii) 0; (viii)
1; (ix) 1; (x) −∞, dividendo per x; (xi) ∞; (xii)√2/(1 + log 3); (xiii) limx→0+ f =
0 6= limx→0− f = 1; (xiv) −∞; (xv) −1; (xvi) 1/ e; (xvii) e (xviii) 0.
18
Da uno degli esercizi di ‘Geometria’ sappiamo che arctan x + arctan 1/x =
±π/2 aseconda che x ≷ 0; allora, (i): prendi x ∈ (0, π/2), cosı̀ limx→0+ f =
limx→0+ x/(x − arctan x) = ∞ perchè limx→0 arctan x/x = 1 ed arctan x < x
(a sua volta perchè x < tan x); (ii): prendi x ∈ (−π/2, 0), cosı̀ limx→0− f =
limx→0+ x/(x − arctan x) = ∞ perchè limx→0 arctan x/x = 1, arctan x > x (a sua
volta perchè x > tan x), e qui il numeratore è negativo.
17(i)