Diapositiva 1 - Dipartimento di Chimica

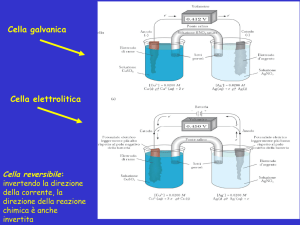
Quando due elettrodi vengono immersi in una
soluzione e si applica una differenza di potenziale tra
essi, si osserva il passaggio di una corrente nel
circuito esterno.
Il meccanismo di comunicazione elettrica tra i due
elettrodi nella soluzione è dovuto al movimento degli
ioni in soluzione.
Quando
non
c’è
un
apprezzabile, l’intensità
segue la legge di Ohm:
processo
di
della corrente
elettrolisi
osservata
V  iR
1
Prendono il nome di elettroliti tutte le sostanze dissociabili in
ioni. Sono quindi elettroliti gli acidi, le basi e i sali. Le
soluzioni acquose di elettroliti (soluzioni elettrolitiche),
grazie al fatto che questi si dissociano in ioni, conducono la
corrente elettrica.
Il cloruro di sodio, come tutti i sali, allo stato cristallino è
isolante. In acqua i cristalli di NaCl si scindono negli ioni
che li costituiscono: lo ione positivo sodio (Na+) e lo ione
negativo di cloro (Cl-).
2
3
Dal punto di vista macroscopico la conduzione della
corrente in soluzione è come la conduzione
dell’elettricità attraverso un oggetto metallico.
La classificazione classica della fisica dei diversi tipi di conduttori
elettrici è:
CONDUTTORI DI PRIMA SPECIE: appartengono a questa
categoria tutti i metalli.
CONDUTTORI DI SECONDA SPECIE: appartengono a questa
categoria tutte le soluzioni elettrolitiche.
CONDUTTORI GASSOSI: particolari condizioni di ionizzazione dei
gas (plasma)
ISOLANTI: sostanze covalenti in cui gli elettroni non sono liberi di
muoversi.
SEMICONDUTTORI:
sostanze
caratterizzate
da
un
comportamento intermedio tra i conduttori e gli isolanti (per es. a
basse T sono isolanti mentre aumentando la T aumentano le
4
capacità di conduzione elettrica).
In realtà i conduttori di elettricità possono essere classificati in tre
distinte categorie:
1. conduttori metallici, nei quali sono presenti elettroni liberi che sotto
l'azione di un campo elettrico anche molto debole vengono convogliati in
un flusso ordinato unidirezionale;
2. conduttori elettrolitici, nei quali il passaggio dell'elettricità è dovuto
ad un doppio flusso, in direzioni opposte, di ioni positivi e negativi, ed è
quindi accompagnato da trasporto di materia;
3. conduttori gassosi, nei quali il flusso di elettricità è dovuto al moto
di ioni gassosi o anche di elettroni liberi: gli uni e gli altri si formano in
condizioni particolari, per esempio per l'azione di scariche elettriche o
di radiazioni ovvero per ionizzazione di atomi o molecole a temperatura
molto alta.
La conducibilità elettrica di una soluzione elettrolitica, intesa in
senso generico come la sua capacità di condurre la corrente per
trasporto degli ioni in essa presenti, dipende da diversi fattori
quali la concentrazione degli ioni, la loro carica, la loro
mobilità e la temperatura. Le grandezze più significative per
esprimere la conducibilità delle soluzioni elettrolitiche sono la
conduttanza specifica o conduttività e la conduttanza
5
equivalente.
In una soluzione elettrolitica, più elevata è la
concentrazione degli ioni, più basso è il valore della
resistenza R della soluzione, quindi la corrente che
passa in una soluzione può essere correlata alla
concentrazione degli ioni.
N.B.: Bisogna sottolineare, però, che la distanza tra gli
elettrodi, l’area superficiale degli elettrodi stessi e il tipo di
ioni disciolti influenzano moltissimo il valore di R.
6
l
R r
A
l = lunghezza del conduttore (cm)
A = sezione del conduttore (cm2)
R= resistenza espressa in Ohm (W)
r = resistenza specifica o resistività (W ∙ cm)
Mentre le caratteristiche elettriche dei conduttori metallici sono
abitualmente studiate prendendo in esame la loro resistenza R, le
caratteristiche elettriche delle soluzioni sono studiate prendendo in
esame la loro conduttanza Λ definita come l'inverso della sua
resistenza R.
1

R
Il significato fisico di questa grandezza è chiaro: la
conducibilità di un conduttore è una misura della sua
capacità di farsi attraversare da una corrente elettrica.
L'unità di misura della conducibilità è il Siemens
(simbolo S) e dalla definizione si deduce che
1 S = 1 W-1.
7
NB: La conducibilità 
si può anche indicare
con la lettera G
8
Esistono
diversi
simboli
conducibilità specifica, di
lettere dell’alfabeto greco:
k
per
esprimere
la
solito si utilizzano
g c
in analogia con il testo consigliato per lo studio
teorico la conducibilità specifica verrà indicata
con la k.
La quantità k, chiamata conducibilità specifica,
contiene tutte le informazioni chimiche relative alla
sostanza considerata (per es. concentrazione e
mobilità degli ioni presenti) e rappresenta le proprietà di
trasporto globali di una soluzione elettrolitica .
9
La quantità S/l è un fattore costante per
il particolare tipo di cella di misura ed è
chiamata costante di cella k:
1 S k S
l


k  
R l
l
S
S
k
l
Se poniamo S = 1 cm2 e
l=1 cm, otteniamo =k,
cioè la conducibilità
specifica k di una soluzione
si identifica con la
conducibilità dovuta gli ioni
contenuti in un volume di 1
cm3 di soluzione
10
CONDUCIBILITÀ SPECIFICA: CARATTERISTICHE
Poiché il passaggio di corrente elettrica in una soluzione è possibile grazie al
movimento degli ioni in essa contenuti, la k di una soluzione sarà tanto
maggiore quanto maggiore è la concentrazione di specie ioniche
presenti.
Inoltre, a parità di concentrazione, la k sarà tanto maggiore quanto più
facile è il movimento degli ioni nella soluzione.
 La k diminuisce all'aumentare delle interazioni ione-solvente. Queste
dipendono a loro volta da svariati fattori, quali il rapporto carica/raggio
degli ioni o la loro eventuale capacità di instaurare legami idrogeno con
l'acqua.
 Un altro fattore fisico che influisce sulla conducibilità di una soluzione
modificando la mobilità ionica è la viscosità: un'elevata viscosità implica
una bassa mobilità ionica e quindi una bassa k della soluzione.
 Infine k dipende da p e T. L'influenza della p è di solito molto piccola,
mentre la temperatura influisce sulla velocità di migrazione in ragione
di 1-3% per ogni grado Kelvin.
11
Va sottolineato che la conducibilità, come grandezza, contiene
molte più informazioni della semplice concentrazione ionica.
Infatti per esempio la conducibilità di una soluzione 1 M di KCl
sarà sostanzialmente diversa da quella di una soluzione 1 M di
HCl, perché i protoni in soluzione sono molto più mobili degli ioni
potassio.
Tali diversità si possono quantificare considerando un altro
parametro chiamato mobilità (m o u) dello ione.
La mobilità rappresenta essenzialmente quella parte della
conducibilità che è indipendente dalla concentrazione.
Nel caso ideale di uno ione i dipenderà dalla carica ionica
(zi), dal suo raggio di solvatazione (Ri), dalla viscosità del
solvente (h) e dalla carica elementare costante (e)
secondo l’equazione:
zi e
ui 
6h Ri
12
Conduttività dal punto di vista microscopico
ioni
k   zi ci ui F
i
Carica
ione
Concentrazione
ione
Mobilità
ione
mobilità ui
= velocità dello ione i
sotto gradiente di potenziale unitario,
espressa in (cm/s)/(V/cm) = cm2/(V s)
concentrazione ci
solo qui, in mol/cm3
Verifica dimensionale:
(mol e/mol)•(mol/cm3) •(cm/s)/(V/cm)•(C/mol e) = C/(s V cm) = A /(V cm)
= W-1 cm-1 (Dunque coincide con k secondo l’approccio macroscopico)
La conduttività è una grandezza intrinsecamente non selettiva ma “integrale” perché
dipende dai prodotti (carica × concentrazione × mobilità) di tutti gli ioni liberi
nella soluzione studiata
13
La conducibilità specifica sperimentale riflette il
contributo di tutte le specie ioniche mobili presenti in
soluzione, per cui si può riscrivere considerando le
mobilità:
k   zi ui Ci F  
i
i
 zi e
zi 
 6hRi

Ci F


Il significato di questa equazione sta nell’evidenziare
che la conducibilità specifica riflette l’identità dei
singoli ioni, cioè la carica e la mobilità, oltre che la
concentrazione.
14
Influenza della concentrazione
ioni
k   zi ci ui F
i
Per
Cz  A z  a concentrazione c
HCl
k  Fzcu  Fzcu
F = costante di Faraday =96485 C mol e-1
 = grado di dissociazione
k dipende dalla concentrazione sia direttamente
sia indirettamente tramite  ed u.
In particolare si ha:
elettroliti forti: la curva k vs c presenta un
massimo (benché non sempre raggiunto, poichè
all’inizio predomina la crescita di c(tratto
ascendente della curva), poi il calo di  ed u con
la concentrazione ( tratto discendente della
curva);
elettroliti deboli: le mobilità sono circa costanti, la
crescita della concentrazione e del grado di
dissociazione si compensano per cui la curva k vs
c ha un andamento pianeggiante.
K2SO4
KCl
CH3COOH
15
L’esempio dell’acido solforico
82 °C
71 °C
21 °C
33.5% 4.5 M 2.10 V
Accumulatore al piombo:
scarica
PbO2 + Pb + 2 H2SO4 = 2 PbSO4 + 2
H2O
carica
16
Poiché la conducibilità dipende dalla concentrazione, non è facile confrontare
direttamente soluzioni diverse, per cui si usa la conducibilità molare detta
anche conducibilità equivalente, si indica con il simbolo  ed è data da:

k
 eq 
m 
C
k
N
k
M
Esprimibile, per esempio per un elettrolita uni-univalente, anche come:

k
1000C
 F (u  u )
 ha come unità di misura W-1m2eq-1
17
Riepilogando: Parametri che descrivono le proprietà di trasporto di una soluzione
elettrolitica in modo assoluto
1
S
G  k
R
L
k
conduttanza / W1 = f (soluzione,
cella)
Normalizzazione per la costante di
cella
specifica o conduttività / (W1
Fz  cu  Fz  cu conduttanza
cm1) = f (soluzione)
Normalizzazione per la concentrazione
1000k 1000k
conduttanza molare


 F z u  F zu       / (W1 mol1 cm2)
c
c
Approssimazioni per soluzioni molto diluite:
1) Elettroliti forti:
=1
   ( z B2  B1  ) c
Equazione di Onsager
2) Elettroliti deboli CA = C+ + A K = c2/(1)
u circa costante, =/°
a0=ion-size parameter in cm,
1
1
c
B= 0.3291•108 dm3/2 mol-1/2cm-1


B1=0.2300 (mol/dm3)-1/2
  K () 2
B2= 60.65 cm2 W-1 mol-3/2dm-3/2
(a T=25°C)
Equazione di Kraus e
Bray
18
Per ottenere un parametro caratteristico del comportamento di
uno ione in soluzione che fosse indipendente dalla concentrazione,
si tende ad estrapolare il comportamento in condizioni di
diluizione infinita dove si assume che le interazioni elettrostatiche
tra gli ioni siano trascurabili.
Questo processo dà una misura delle proprietà degli ioni
totalmente isolati dal solvente e la quantità estrapolata è detta
conducibilità equivalente o molare a diluizione infinita 0:
0  lim 
C 0
Questo parametro è una somma di contributi dai singoli
ioni in soluzione:
  
0
i
0
i
Legge di Kohlrausch della
migrazione indipendente
degli ioni
Dove 0i sono le conduttività ioniche molari limite, sono
caratteristiche di ciascuno ione ed indipendenti dall’elettrolita di
partenza
19
CONDUCIBILITÀ EQUIVALENTE A DILUIZIONE INFINITA
Esempio: La ° per una soluzione di NaCl sarà:
NaCl  
Na 
 
Cl 
La conducibilità molare a diluizione infinita individuale esprime la capacità di
un dato ione di muoversi sotto l'effetto di un campo elettrico in
assenza di interazioni con altre specie ioniche.
La legge di Kohlrausch permette di esprimere ° come somma di contributi
indipendenti l'uno dall'altro e caratteristici solamente dei cationi ed anioni
presenti nella soluzione; infatti per soluzioni contenenti più di un elettrolita, la
legge si generalizza in:
 
 i
i
dove la sommatoria è estesa a tutte le specie ioniche presenti in soluzione. Ad
esempio, per una soluzione infinitamente diluita contenente NaCl, MgSO4 e
CaCl2 , si ha:
  
Na 
 
Mg2 
 
Ca2 
 
 
SO 2 
4
per questo, la conduttività molare ° a diluizione infinita di un elettrolita
20
si può ricavare per combinazione di dati di ° relativi ad altri elettroliti o di singoli ioni.
Cl 
Alcuni valori delle conducibilità equivalenti limite di singoli ioni sono
riportati nella seguente tabella:
Conducibilità equivalenti limite a 25°C in Acqua
21
L’estrapolazione a diluizione infinita richiede la conoscenza del modo con
cui la conducibilità equivalente dipende dalla concentrazione.
Nei primi del XX secolo Lars Onsager sviluppò una teoria sul movimento
degli ioni in soluzione in cui gli ioni erano considerati piccole particelle
viaggianti in un mezzo dielettrico, in analogia con la teoria di Debye-Hückel
sviluppata per le proprietà di equilibrio delle soluzioni elettrochimiche.
Il risultato più interessante della teoria è questa semplice equazione:

      
0
0

C
 e  rappresentano un insieme di costanti fondamentali e di proprietà,
dipendenti dalla temperatura degli ioni e del solvente. Questa equazione
evidenzia una dipendenza della conducibilità dalla radice quadrata della
concentrazione almeno a bassi valori di C.
22
Per un elettrolita forte, la frazione ionizzata è unitaria per tutte
le concentrazioni, ciò implica che la  è grosso modo costante
Può variare più o meno a causa di variazioni della mobilità ionica,
ma tende ad un valore finito detto 0 a diluizione infinita.
Infatti l’attrazione elettrostatica tra gli ioni riduce le mobilità e si
può dimostrare che per elettroliti forti in soluzioni diluite vale la
relazione:

   1  C
0
)
Legge di Kohlrausch
 dipende, più che dall’identità chimica del composto ionico,
soprattutto dal tipo di elettrolita, nel senso 1:1 MA, 2:1
M2A, etc.
23
Verifica dell’equazione di Onsager per gli elettroliti forti
Conduttività molari a diluizione infinita
°HCl
°K2SO4
°KCl
24
Per una sostanza poco dissociata la conducibilità dipende molto dalla
concentrazione perché il grado di dissociazione varia molto con la
concentrazione.
La conducibilità equivalente, tuttavia, tende ad un valore finito a
diluizione infinita corrispondente di nuovo alla somma delle
conducibilità ioniche limite.
Di solito è impraticabile determinare questo valore limite
dall’estrapolazione dei valori di  a basse concentrazioni, perché per
avere la completa ionizzazione dell’elettrolita, la concentrazione
dovrebbe essere troppo piccola rendendo la conducibilità non
misurabile.
Tuttavia il valore di 0 può essere dedotto dai valori di 0 ottenuti
per gli elettroliti forti e come esempio usiamo l’acido acetico.
25
CH 3COOH  HAc
Si usa l’equazione:
  
0
i
0
i
Che diventa:
0 HAc)  0 HX )  0 MAc )  0 MX )
Dove M+ è un qualunque ione monovalente positivo
tipo K+ o Na + ed X - un qualunque ione negativo tipo
Cl - o Br -. L’unica restrizione su M e X è la necessità
che HX, MAc e MX siano elettroliti forti.
26
0 HAc)  0 HX )  0 MAc )  0 MX )
 HAc )  
0
0
CH3COO

0
CH3COO

0
M


0
H

0
H

0
X

0
M

0
X
27
Se l’elettrolita è sufficientemente debole, la concentrazione
ionica è piccola e l’effetto di attrazione tra gli ioni influenza poco
la mobilità, si può assumere che le mobilità siano indipendenti
dalla concentrazione ottenendo la relazione approssimata:

 0

Per cui misurando la  ad una concentrazione C e calcolando
la 0 dai dati tabulati per gli elettroliti forti si può ottenere il
grado di dissociazione ad una certa concentrazione.
28
Conoscendo la concentrazione C di un elettrolita debole ed il suo grado di
dissociazione a quella concentrazione, si possono conoscere le
concentrazioni dei singoli ioni e della sostanza indissociata. Quindi si può
calcolare la costante di equilibrio e applicando all’esempio dell’acido acetico
si ha:

H Ac 

C

KC
HAc


2
1
N.B.: La KC così calcolata è diversa dalla Ka vera che viene in genere
espressa in termini di attività. Questo sia perché manca il coefficiente di
attività sia perché tali relazioni sono state ottenute con determinate
approssimazioni.
29
Dimostrazione dell’equazione di Kraus e Bray
  F (  zu   zu )
costante di dissociazione di un elettrolita
debole, ad esempio uniunivalente, in
funzione del grado di dissociazione,
trascurando i coefficienti di attività gi
  F (  z  u     z  u  )
Hp per elettrolita debole: mobilità circa costanti
(il numero di particelle è sempre molto basso)

 2c 2
 2c
Ka 

1   )c 1   )


Ka 
c2
     ) )
1
1
c


   K a (  )2
30
La conduttimetria è una tecnica strumentale che consente di misurare la
conducibilità elettrica di una soluzione elettrolitica riferendosi alla corrente
che passa in una porzione chiamata cella conduttimetrica. La cella
conduttimetrica è costituita da due elettrodi in genere di platino platinato a
distanza "l" e di superficie "S".
31
La misura della conducibilità
prende le mosse dalla misura
della resistenza che
normalmente viene effettuata
con un dispositivo detto
ponte di Wheatstone.
X è la resistenza incognita da misurare; R è una cassetta di resistenze
di valore noto; G è un galvanometro (o Amperometro) a zero centrale;
P è una batteria; T è un interruttore; AB è un filo omogeneo calibrato
teso su un regolo millimetrato. In condizioni di equilibrio del ponte,
quando tra i punti C e D non c’ è d.d.p e il galvanometro non segnala
passaggio di corrente, la resistenza incognita X può essere
determinata mediante la seguente relazione:
l2
RX  R
l1
32
33
Per la misura di conducibilità
si utilizza un ponte di
Wheatstone modificato,
detto ponte di Kohlrausch.
Il principio di funzionamento
è lo stesso solo che lavora
in corrente alternata.
34
La misura di conduttività di una soluzione elettrolitica si esegue in corrente
alternata in modo da evitare polarizzazione o addirittura processi
elettrolitici agli elettrodi.
Però una soluzione non è un conduttore puramente ohmico.
I circuiti non puramente ohmici percorsi da corrente alternata risentono di
effetti induttivi e/o capacitivi che sono funzione della frequenza della
corrente impiegata.
Cioè, mandando una tensione alternata sulla cella di conduttività e
misurando la corrente, la risposta del sistema non è di una resistenza
ohmica, ma di una impedenza Z, cioè la somma vettoriale della resistenza
ohmica R e di termini resistivi corrispondenti agli elementi capacitivi e
induttivi presenti nel circuito, rispettivamente “reattanze capacitive XC ” e
“reattanze induttive XL”.
35
A13. Lo strumento storico: il ponte di Kohlrausch
Poiché si può considerare la cella
di conduttività equivalente ad una
R e una C in parallelo, lo
strumento storico per le misure di
resistenza di una soluzione
elettrolitica, il ponte di
Kohlrausch, permetteva di
effettuare la misura bilanciando il
parallelo RxCx della cella variando
un parallelo campione RcCc fino
ad azzerare il modulo e lo
sfasamento della corrente alternata
nel ramo centrale del ponte.
36
G:Generatore di corrente
alternata
Rx :Resistenza della cella
immersa nella soluzione in
esame
R:Resistenza nota e variabile
R1:Resistenza del tratto AS
R2:Resistenza del tratto AH
M:Strumento sensibile al
passaggio di corrente anche
di piccola intensità
(microamperometro)
Quando si esegue la misura, si muove la resistenza variabile fino a quando M
segna una corrente nulla. Quando M segna corrente nulla si dice che il ponte è in
equilibrio. Quando il ponte è in equilibrio valgono le seguenti condizioni:
(1) VS = VH e quindi VAS = VAH e VBS = VBH
(2) Ix = IAH e IAS = IBS
nei quattro lati del ponte.
dove Ix , IAH , IAS , IBS sono le correnti elettriche
37
Per la prima legge di Ohm sarà :
VAH = R2•IAH
VAS = R1•IAS
VBS = R • IBS
VBH = RX • IX
Combinando la condizione (1) con la prima legge di Ohm si avranno le seguenti
uguaglianze:
R2•IAH = R1•IAS ; R • IBS = RX • IX
dividendo membro a membro le due uguaglianze si ottiene:
R1  I AS
RX  I X

R  I BS
R2  I AH
se si tiene conto della seconda condizione (2) di equilibrio, del ponte, si ottiene :
RX R1
R1

 RX  R 
R
R2
R2
38
39
Celle conduttimetriche industriali
Celle a
deflusso
Celle a
immersione
Industrialmente si usano elettrodi di acciaio inossidabile (o di grafite) con parti isolanti di resina: sono
più semplici, robusti e poco costosi, ma con prestazioni inferiori, specie per resistenze molto basse
(conduttività molto alte)
40
particolarmente utili, montati su bypass delle tubazioni principali, per controlli industriali in continuo.
41
Applicazione di misura diretta:
valutazione semiquantitativa della durezza(I)
Acque di acquedotto
Acque minerali
La “durezza” è uno dei parametri fondamentali di un’acqua naturale
Il termine deriva dalla terminologia delle lavandaie di un tempo, per le quali un’acqua era tanto più “dura”
quanto maggiore era la quantità di sapone richiesta per produrre la schiuma.
Essa è associata alla presenza di cationi polivalenti in grado di causare la precipitazione di composti
insolubili dai saponi alcalini usati come detergenti
Si tratta prevalentemente degli ioni Ca2+ e Mg2+, benché contribuiscano anche gli altri cationi del secondo
gruppo Ba2+ e Sr2+ (e anche altri cationi come ferro, manganese, zinco…)
Si misura in gradi francesi °f definiti come
tutti gli ioni di durezza espressi come mg
CaCO3 per 100 cm3 di prelievo
(oppure gradi francesi °d definiti come
tutti gli ioni di durezza espressi come mg CaO per
42
100 cm3 di prelievo
Applicazione di misura diretta:
valutazione semiquantitativa della durezza (II)
Durezza temporanea
Durezza totale
Cationi di metalli alcalino terrosi
(soprattutto Ca2+ e Mg2+) presenti
in combinazione con anioni sia di
acidi forti (Cl, SO4=, NO3) sia di
acidi deboli (HCO3).
durezza totale =
durezza permanente
+ durezza temporanea
Alcune tra le molte classificazioni:
Porzione che scompare se si fa bollire l’acqua.
Corrisponde ai bicarbonati dei cationi di metalli
alcalino terrosi (che durante l’operazione
suddetta
precipitano
sotto
forma
dei
corrispondenti carbonati con perdita di CO2):
ad es. Ca(HCO3)2 
ebollizione
CaCO3 + CO2+ H2O
Durezza permanente
Porzione che rimane se si fa bollire l’acqua.
Corrisponde ai cationi di metalli alcalino terrosi
presenti nel campione in combinazione con
anioni di acidi forti
leggere o dolci:
mediamente dure:
dure:
durezza inferiore a 15 °F durezza tra 15 e 30 °F durezza superiore a 30 °F
“Calciche” se Ca2+ > 150 mg/dm3 (cioè se Ca2+ da solo
è >37.5 °F)
Attive su stomaco e fegato; indicate nella gravidanza, nella
crescita e nella prevenzione della osteoporosi
“Contenenti bicarbonato” se HCO3 > 600 g/dm3
Indicate per stimolare la secrezione gastrica e nelle
patologie renali
“Magnesiache” se Mg 2+ > 50 mg/dm3 (cioè se Mg2+
da solo è >20.6 °F)
Svolgono prevalentemente attività purgativa; trovano
indicazioni anche della prevenzione della arteriosclerosi
43
Applicazione di misura diretta:
valutazione semiquantitativa della durezza (IV)
Per determinare con precisione (a) la durezza totale e (b) quella temporanea
si esegue una titolazione rispettivamente
(a) degli ioni calcio e magnesio e (b) degli ioni bicarbonato
Per differenza poi si determina la durezza temporanea
Tuttavia, la durezza totale delle acque si può stimare con
buona approssimazione mediante una semplice misura
conduttimetrica.
E’ quello che si fa correntemente soprattutto come prova
preliminare per calibrare opportunamente le analisi
specifiche successive.
44
Alcune acque minerali da tavola italiane
45
46
Applicazione di misura diretta:
monitoraggio dell’acidità libera in acidi organici ad elevatissima concentrazione
Problema: stimare l’acidità di soluzioni per l’esfoliazione della pelle, prima di
sperimentarle su pazienti
Effettuando misure di pH
con il protocollo acquoso
(standard, elettrodo di
riferimento, ponte salino) si
osserva che risultano
raggruppate in un range
molto ristretto (1.5 unità
pH), molto poco
differenziate a seconda
dell’acido, e soprattutto
non seguono affatto la
formulazione del mezzo
acquo-organico
In questo importante caso applicativo il pH risulta
inutilizzabile per scopi di formulazione e controllo
47
Una possibile soluzione del problema:
monitorare l’acidità libera attraverso la conduttività
La conduttività è una
grandezza
intrinsecamente non
selettiva ma “integrale”
perché dipende dai
prodotti (carica ×
concentrazione ×
mobilità) di tutti gli
ioni liberi nella
soluzione studiata
ioni
k   zi ci ui F
i
Carica
ione
Mobilità
ione
Concentrazione
ione
Tuttavia,
a) in soluzioni acquose o miste ma con percentuale significativa di acqua il
contributo di gran lunga più significativo alla conduttività é quello degli ioni H+
b) nel nostro caso paragoniamo soluzioni di acidi deboli monoprotici HA a
solvente costante oppure lo stesso acido al variare del solvente o della
temperatura  la grandezza si può considerare un sensibile e affidabile
indicatore di disponibilità e mobilità dei protoni
48
Costanti di dissociazione acida Ka nettamente e correttamente differenziate
Andamenti lievemente parabolici estremamente regolari
La conduttività cala regolarmente al calare della % DMI
Il calo è sempre più accentuato all’aumentare della forza dell’acido
49
Applicazione come parametro per seguire titolazioni:
titolazioni conduttimetriche acido/base (I)
In generale nelle titolazioni per neutralizzazione, precipitazione, scambio, ecc. ci si possono
attendere cambiamenti di conduttività che si possono sfruttare per seguire il decorso della reazione
e soprattutto individuare il punto finale.
Ovviamente si può eseguire una titolazione conduttimetrica seguendo della soluzione la
conduttività o anche solo la conduttanza, che è ad essa proporzionale.
La temperatura deve essere pressochè costante, ed è preferibile che anche il volume della soluzione
non cambi troppo durante la titolazione.
A differenza delle curve di titolazione potenziometriche,
•i punti di equivalenza non corrispondono a flessi, ma ad angoli d’intersezione tra tratti rettilinei.
L’accuratezza del metodo è tanto maggiore quanto più acuto è l’angolo d’intersezione, e quanto
maggiore è la correlazione lineare dei punti sperimentali;
•non hanno particolare senso accurate misure vicino al punto di equivalenza, anzi, a causa di
idrolisi, dissociazione, o solubilità del prodotto della reazione nei pressi del punto di equivalenza il
grafico di titolazione in tale zona risulta arrotondato e quindi il punto di equivalenza si valuta
estrapolando i tratti rettilinei e valutandone il punto d’intersezione.
I vantaggi delle titolazioni conduttimetriche rispetto a quelle colorimetriche e potenziometriche
sono:
•Il metodo è accurato tanto in soluzioni diluite che concentrate
•Il metodo funziona bene in casi altrimenti critici come titolazioni di acidi deboli con basi
deboli e titolazioni di acidi debolissimi come fenoli, acido borico...
Rispetto alle colorimetriche:
50
•Il metodo funziona anche con soluzioni torbide
A24. Applicazione come parametro per seguire titolazioni:
titolazioni conduttimetriche acido/base (II)
k (o G)
cala forza o
concentrazio
ne acido
cala forza
base
VT
Hp: temperatura, volume e mobilità
ioniche circa costanti
51
Nel primo tratto la conduttività cala perchè lo ione
H+ (il più mobile, °H+  350 1cm2mol1) viene
sostituito da Me+ (°Me+  40/80 1cm2 mol1); dopo il
punto di equivalenza ricresce al crescere dell’eccesso
di OH (°OH  198 1cm2 mol1).
Nel primo tratto la conduttività cala perchè
lo ione H+ (il più mobile, °H+  350
1cm2mol1) viene sostituito da NH4+; dopo
il punto di equivalenza resta pressochè
costante perchè NH3 in eccesso ha su di essa
un’influenza trascurabile rispetto al sale
(NH4)2SO4 .
52
53
Qualsiasi cella conduttimetrica è caratterizzata dalla
propria costante di cella L/S (in cm1) o S/L (in cm), e,
nel caso di forme geometriche semplici, teoricamente
potrebbe essere calcolata dalla lunghezza L e sezione
attiva S del conduttore, mentre nel caso di forme
irregolari, si dovrebbe sviluppare un integrale.
Però, soprattutto a causa della geometria non ideale
delle linee di corrente e dell’uso di superfici conduttrici
complesse è molto meglio operare una taratura
misurando la  di una soluzione campione di cui è nota
con precisione la k e utilizzando la k/  = (L/S).
54
Per conoscere la costante della cella di conducibilità in uso si
utilizzano soluzioni a concentrazione nota di KCl a 25°C.
La conducibilità delle soluzioni di elettroliti forti è stata interpolata
sperimentalmente con l’equazione della legge di Fuoss-Onsager:
   0  S C  EC log C  JC
Questa legge è una elaborazione della più semplice
legge di Onsager che prevedeva solo una dipendenza
della  da √C.
Per il KCl l’equazione precedente diventa:
  149.93  94.65 C  58.74C log C  194.4C
Ed è valida a 25°C per concentrazioni: 0≤C≤0.012 M
55
Si preparano 4 soluzioni di KCl a diversa concentrazione e si mettono
a termostatare.
In particolare si diluisce una soluzione madre di KCl 0.01 M in
matracci tarati da 100 ml portando a volume con acqua bidistillata:
ml KCl 0.01 M
20
40
60
80
56
Si misurano le resistenze delle soluzioni preparate e della
soluzione madre (0.01 M) e per ciascuna soluzione si calcola la
concentrazione molare e la conducibilità dall’equazione vista prima.
La costante di cella k sarà ottenuta dalla media dei valori
determinati con la relazione classica:
1000  k

R C
57
Tale determinazione si basa sulla misura della
conducibilità della soluzione dell’acido, mettendola in
relazione con  (grado di dissociazione)
dell’elettrolita nella situazione di equilibrio.
Si ricorda che esiste la seguente relazione, ricavata
per la prima volta da Arrhenius:


0
58
Si suppone di avere un acido debole così dissociato:


HA  H  A

H A 


K
C
a

HA
Sapendo che all’equilibrio:
A   H     C


HA  C  (1   )
 C

1
2
K
C
a
Introducendo la dipendenza di  dalla conducibilità si ha:
2

C
2
0
C
Ka 

(1  )
0
Legge di diluizione di
OSTWALD
59
La legge di Ostwald può essere riarrangiata attraverso una serie di
banali operazioni ottenendo:
 mc
1
1
 o 
2
o
m m Kam
Si può rappresentare come l’equazione di una retta:
1/my
mC=x
60
1
1
c


  K () 2
1/(K°)2
1/°
CH3COOH
61
 Si usa una soluzione 0.1 M di acido acetico in acqua
bidistillata.
 Si diluisce in 5 matracci da 100 ml prelevando con una
buretta 5, 10, 15, 30, 50 ml della soluzione madre e portando
a volume con acqua bidistillata.
 Si misura la resistenza di ciascuna soluzione termostatata a
25°C
 Si calcola poi la m di ciascuna soluzione
 Si riporta in grafico m•C in funzione di 1/ m e si
interpolano i dati sperimentali con i minimi quadrati.
62
Effect of Concentration on Conductivity: HCl e CH3COOH
Small volumes, 1.00 mL increments, of
1.00 M HCl (5 aggiunte) or CH3COOH (7
aggiunte) are added to 60.0 mL of water
and conductivity is
measured after each addition
Effect of Temperature on the Conductivity of a 0.10 M NaCl:
Temperature and conductivity measurements are made
every 30 s on a 0.10 M NaCl aqueous solution cooled by an
ice bath.
Effect of Charge
Conductivity of 0.0010 M NaClO4 and 0.0010 M MgSO4
are measured.
Effect of Anion Size and Mass
Conductivity of 0.10 M NaCl, 0.10 M NaBr, 0.10 M NaI,
and 0.10 M NaClO4 are measured.
63