Lezione n. 3

Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
7 – VARIABILI E FUNZIONI
“Introduzione a DERIVE”
In DERIVE si possono definire sia variabili che funzioni.
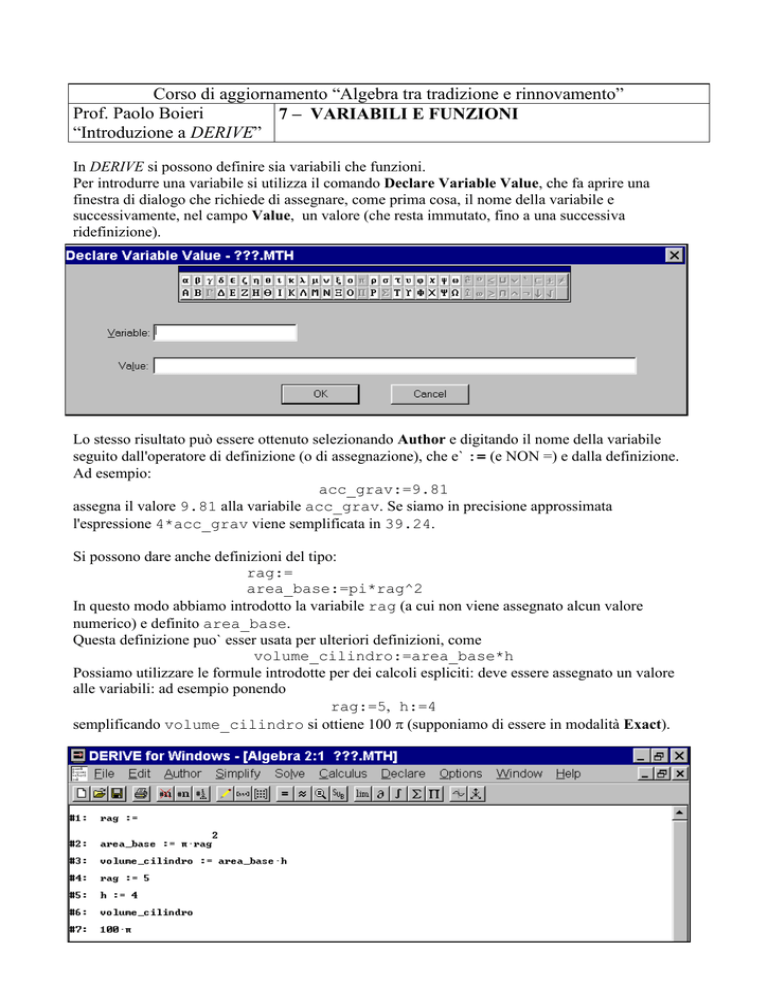
Per introdurre una variabile si utilizza il comando Declare Variable Value, che fa aprire una
finestra di dialogo che richiede di assegnare, come prima cosa, il nome della variabile e
successivamente, nel campo Value, un valore (che resta immutato, fino a una successiva
ridefinizione).
Lo stesso risultato può essere ottenuto selezionando Author e digitando il nome della variabile
seguito dall'operatore di definizione (o di assegnazione), che e` := (e NON =) e dalla definizione.
Ad esempio:
acc_grav:=9.81
assegna il valore 9.81 alla variabile acc_grav. Se siamo in precisione approssimata
l'espressione 4*acc_grav viene semplificata in 39.24.
Si possono dare anche definizioni del tipo:
rag:=
area_base:=pi*rag^2
In questo modo abbiamo introdotto la variabile rag (a cui non viene assegnato alcun valore
numerico) e definito area_base.
Questa definizione puo` esser usata per ulteriori definizioni, come
volume_cilindro:=area_base*h
Possiamo utilizzare le formule introdotte per dei calcoli espliciti: deve essere assegnato un valore
alle variabili: ad esempio ponendo
rag:=5, h:=4
semplificando volume_cilindro si ottiene 100 (supponiamo di essere in modalità Exact).
Scheda n. 7 – Variabili e funzioni. Pag.
2
IL COMANDO DECLARE FUNCTION DEFINITION
Supponiamo di dover utilizzare spesso in una seduta di lavoro una funzione: ad es.
1 x
log
.
1 x2
Per evitare di digitarla in continuazione possiamo introdurre una nuova funzione a cui assegniamo il
valore LOG((1+x)/(1+x^2)).
Con il comando Declare Function Definition appre una finestra di dialogo in cui dobbiamo
dapprima introdurne il nome, (che supponiamo essere ff(x), si noti che nella versione per
Windows è necessario anche indicarne esplicita l’argomento o gli argomenti), poi la definizione
(che è LOG((1+x)/(1+x^2))). Confermiamo con OK.
DERIVE analizza l'espressione, quindi appare la definizione:
Si noti ancora la presenza dell'operatore di assegnazione := e il fatto che le funzioni pre-esistenti e
nuove sono riscritte in maiuscolo, indipendentemente da come sono state introdotte, se si usa
Declare, Algebra State, Input Options, Case Sensitivity = Insensitive (vedi Capitolo 3).
Un modo equivalente di introdurre la funzione è quello di selezionare Author e digitare direttamente
nella linea di editing la definizione della funzione: FF(x):=LOG((1+x)/(1+x^2)) (non e`
essenziale la maiuscola nella scrittura dei nomi delle funzioni; è invece essenziale indicare
esplicitamente le variabili).
Nella definizione di una funzione si possono utilizzare le funzioni predefinite di DERIVE e le
funzioni introdotte in precedenza dall'utente.
Ad esempio, se introduciamo la distanza dall'origine nello spazio
R(x,y,z):=SQRT(x^2+y^2+z^2)
possiamo definire, a partire da essa, il potenziale newtoniano
NEW_POT(x,y,z):=1/R(x,y,z).
Se introduciamo NEW_POT(x,y,z) e selezioniamo Simplify otteniamo
1/SQRT(x^2+y^2+z^2).
Scheda n. 7 – Variabili e funzioni. Pag.
3
Possiamo valutare una funzione in un punto del suo dominio: scriviamo la funzione e poi
utilizziamo il comando Simplify, Sustitute for, Variables, indicando i valori da assegnare alle
variabili:
appare la seguente finestra di dialogo:
Evidenziamo ad una ad una le tre variabili indicate e digitiamo i corrispondenti valori nel campo
Substition: 1, 1, 5, rispettivamente per x, y, z; confermiamo con OK. Successivamente
selezioniamo Simplify:
In alternativa, possiamo scrivere direttamente i valori da sostituire alle variabili; questi valori
possono anche essere simbolici: selezioniamo Author, digitiamo NEW_POT(1,1,z^2),
confermiamo con OK poi selezioniamo Simplify:
OSSERVAZIONE 1
Per definire il volume del cilindro possiamo procedere in un modo diverso da quello indicato sopra,
introducendo una FUNZIONE. Poniamo
VOL_CILINDRO(rag,h):=pi*rag^2*h
La differenza sostanziale tra i due procedimenti sta nel modo in cui vengono effettuate le
valutazioni. In questo secondo caso assegniamo i valori di rag e di h come argomenti della
funzione:
Scheda n. 7 – Variabili e funzioni. Pag.
4
VOL_CILINDRO(5,4)
che semplificato fornisce:
OSSERVAZIONE 2
Un'interessante caratteristica è quella di potere introdurre delle funzioni senza definizione esplicita.
Per fare questo:
1) selezionando il menu Declare, Function Definition si apre una finestra di dialogo; nel campo
Name and Arguments si introduce il nome della funzione (ad esempio f(x))
2) nel campo Definition non si scrive nulla;
3) si seleziona OK per confermare.
Lo stesso effetto è ottenuto digitando nella linea di editing attivata con Author: f(x):=
Un esempio: a partire dalle funzioni senza definizione esplicita
F(x):=
G(x):=
definiamo la funzione
PROD(x):=F(x)*G(x)
Ora possiamo chiedere, ad esempio, il calcolo della derivata prima e quarta di PROD(x), ottenendo
la `regola di derivazione':
Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
8 – IL DOMINIO DI UNA VARIABILE
“Introduzione a DERIVE”
In DERIVE alcune semplificazioni sono automatiche e non presentano problemi: ad esempio
x + 0 = x , oppure x*1=x.
In altri casi si possono presentare ambiguità o risultati inaspettati. Ad esempio, l'espressione
sqrt(x^2) puo` essere semplificata in vari modi, a seconda dell'insieme a cui appartiene x.
Selezionando Declare, Variable Domain si apre una finestra di dialogo nella quale va indicato il
nome della variabile desiderata (per esempio x):
Confermando con Declare, si appre un’altra finestra di dialogo con opzioni relative al Domain
(Integer, Real, Complex, Nonscalar).
Complex e Nonscalar saranno viste piu` avanti.
Se scegliamo Integer (interi relativi) o Real (reali) è attivo anche il sottomenu Interval con le voci:
All, Positive, Negative ecc:
Scheda n. 8 – Il dominio di una variabile. Pag.
2
Per alcune voci il significato e` ovvio: All: x reale, Positive: x>0, Negative: x<0, Nonpositive:
x<=0, Nonnegative x>=0.
Selezionando una delle opzioni relative a Interval (aperto, chiuso, aperto a sinistra, aperto a destra)
si attiva un ulteriore sottomenu Bounds (= Estremi) che consente di definire l’estremo inferiore
(Lower) e superiore (Upper) dell’intervallo.
L’estremo inferiore o quello superiore possono essere, rispettivamente, (si scrive – inf),
oppure  (si scrive +inf).
La scelta del dominio viene visualizzata.
Nell'esempio che segue abbiamo varie semplificazioni di sqrt(x^2) in funzione del dominio:
Analogamente l'espressione sqrt(-x):
Come conclusione, si deve ricordare che DERIVE non esegue semplificazioni se non dopo averne
verificato la validità nel dominio assegnato e che il dominio di default è Real All.
Un esempio: l'espressione cos(k) non viene semplificata perché k è considerato (di default)
reale e quindi non ha senso alcuna semplificazione; ridefinendolo come Integer, abbiamo invece:
Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
9 – I NUMERI COMPLESSI E LE FUNZIONI
“Introduzione a DERIVE” COMPLESSE
"Per utilizzare bene DERIVE è necessario conoscere i numeri complessi; infatti DERIVE usa in
molte situazioni funzioni a valori complessi producendo risultati a volte inaspettati.
Nella prima parte introduciamo le operazioni elementari sui complessi, mentre nella seconda
esaminiamo queste questioni più delicate, che riguardano soprattutto radici e logaritmi.
OPERAZIONI SUI NUMERI COMPLESSI
L'unità immaginaria viene introdotta scrivendo #i (e NON semplicemente i) oppure selezionando
î nell’elenco di caratteri che appare selezionando Author.
DERIVE svolge le operazioni sui numeri complessi in forma cartesiana (negli esempi che seguono
la semplificazione è resa automatica dalla digitazione in Author dell’espressione seguita dal
simbolo di =, come descritto nel Capitolo 1):
Assegnato un numero complesso z in forma cartesiana, grazie ad alcune funzioni predefinite,
possiamo definire:
1) la parte reale RE(z)
2) la parte immaginaria IM(z)
3) il modulo ABS(z)
4) l'argomento PHASE(z) (misurato dal semiasse reale positivo in verso antiorario e con la
limitazione - pigreco < PHASE(z) <= Pigreco)
5) il complesso coniugato CONJ(z)
6) il numero complesso di modulo unitario u associato a z e definito da u = z/|z|, indicato con
SIGN(z).
Scheda n. 9 – I numeri complessi e le funzioni complesse. Pag.
4
Osserviamo che si possono svolgere le operazioni e applicare le funzioni anche al numero
complesso scritto nella forma simbolica x + i y.
Questo è molto utile nelle applicazioni della teoria delle funzioni di variabile complessa.
RADICI
La radice quadrata di x è indicata con il simbolo Sqrt(x), mentre la radice n-esima viene indicata
con x^(1/n).
Quando si lavora, in modalita` EXACT, con reali positivi non ci sono problemi: le radici sono
lasciate in forma simbolica oppure, se possibile, sono semplificate:
Vengono effettuate le semplificazioni delle potenze del tipo x^(m/n):
Se invece x è reale negativo, DERIVE, per default, fornisce la radice principale (o primitiva)
complessa: ricordiamo che, assegnato un numero complesso z, si dice radice primitiva di z il
Scheda n. 9 – I numeri complessi e le funzioni complesse. Pag.
5
numero complesso che ha come modulo la radice n-esima di |z| e come argomento il valore
arg(z)/n mentre le altre radici hanno come modulo la radice n-esima di |z| e come argomento i
valori (arg(z) + 2 k )/n k=1,2,...n-1.
Per ottenere la (eventuale) radice reale bisogna utilizzare il menu Declare, Algebra State,
Simplification e, nel campo Branch, selezionare l'opzione Real:
oppure selezionare Author e digitare direttamente Branch:=Real.
Se il numero non ha radici reali, viene scritta la radice fondamentale:
Quando si utilizzano funzioni irrazionali, per avere risultati corretti è a volte NECESSARIO
dichiarare il dominio di una variabile.
L'esempio seguente mostra le diverse semplificazioni dell'espressione
 x  2 x  3 :
Scheda n. 9 – I numeri complessi e le funzioni complesse. Pag.
6
Scegliendo l’opzione Real nel campo Branch, per x Real nessuna semplificazione:
Per x > 3 si ha il prodotto di due radicali che hanno come argomento funzioni positive; dovremo
selezionare nel menu Declare, Variable Domain, relativamente alla variabile x, l’opzione Closedopen interval con estremi 3 e infinito:
Lo stesso avviene per x < 2: in questo caso dobbiamo cambiare segno negli argomenti delle radici,
sempre per avere una quantità positiva:
Nell'intervallo 2 < x < 3 il fattore SQRT(x-2) non pone problemi, mentre l'altro viene scritto
facendo intervenire l'unità immaginaria:
Osserviamo ora le diverse semplificazioni dell' espressione
confrontare con i risultati precedenti:
x  2  x  3 che invitiamo a
In particolare abbiamo ottenuto un risultato reale (e negativo!) in (-inf,2], in contraddizione
con quanto si ottiene lavorando solo in ambito reale.
LOGARITMI
Assegnato un numero complesso z il suo logaritmo è dato da
ln z = ln |z| + i (arg z + 2 k ), con k intero relativo.
Scheda n. 9 – I numeri complessi e le funzioni complesse. Pag.
Per k = 0 si ha il logaritmo principale (ricordiamo che < arg z  ).
DERIVE fornisce il logaritmo principale complesso:
L'esempio seguente mostra come ci vuole cautela nell'uso di identità come ln(xy)=ln x + ln y,
quando gli argomenti non sono entrambi positivi.
7
Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
10 – VETTORI E MATRICI
“Introduzione a DERIVE”
Vettori e matrici hanno un'importanza fondamentale in DERIVE, in quanto, oltre a permettere
l'esecuzione delle usuali operazioni vettoriali e matriciali, sono strutture fondamentali della
programmazione.
Iniziamo vedendo l'utilizzo di queste strutture per gli usuali calcoli.
Un vettore può essere introdotto mediante il comando Author Vector: in questo caso si apre una
finestra di dialogo nella quale va inserita la dimensione del vettore:
Dopo aver confermato con OK si apre un’altra finestra di dialogo nella quale vengono introdotte le
componenti, che possono essere sia numeri che funzioni:
Un altro modo di introdurre un vettore è quello di assegnarne le componenti, scrivendole tra
parentesi QUADRE nella linea di editing che si attiva selezionando Author:
Scheda n. 10 – Vettori e matrici. Pag.
E` possibile sommare due vettori della stessa dimensione, componente a componente (espressione
#1), moltiplicare un vettore per uno scalare (espressione #2), eseguire il prodotto scalare di due
vettori della stessa dimensione (espressioni #3 e #4); anche in questi esempi la semplificazione è
resa automatica attraverso l’inserimento del simbolo di uguaglianza dopo l’espressione:
Per vettori con tre componenti si calcola il prodotto vettoriale Cross. Se i vettori hanno due
componenti si ottiene uno scalare (la terza componente del prodotto vettoriale dei vettori, pensati
con terza componente nulla):
Una matrice può essere introdotta con il comando Author Matrix: compare una finestra di dialogo
nella quale si assegnano le dimensioni:
Dopo aver confermato con OK compare una nuova finestra di dialogo con la matrice già impostata
nella quale vanno inseriti, nella posizione appropriata, tutti gli elementi.
2
Scheda n. 10 – Vettori e matrici. Pag.
In alternativa si puà selezionare Author e digitare la matrice come vettore di vettori: ogni vettore è
una RIGA della matrice. Ad esempio la matrice
a b c d 
 e f g h


sarà scritta come: [[a,b,c,d],[e,f,g,h]].
Bisogna notare la differenza tra queste tre scritture, che coinvolgono gli stessi elementi:
- vettore, introdotto scrivendo [a,b,c], che appare sullo schermo alla linea # 8;
- matrice 1 x 3 (una riga e tre colonne), introdotta scrivendo [[a,b,c]], che appare sullo
schermo alla linea # 9 (si noti che gli elementi di matrice non appaiono separati da virgole);
- matrice 3 x 1 (tre righe e una colonna), introdotta scrivendo [[a],[b],[c]] che appare sullo
schermo alla linea #10.
Assegnata una matrice, si può ottenere la sua trasposta, che si indica con il simbolo ` (accento
grave); se non compare sulla tastiera, questo simbolo si ottiene tenendo premuto Alt e battendo 96
sul tastierino numerico oppure “cliccando” con il mouse sul corrispondente simbolo presente al di
sopra della linea di editing. La trasposta si ottiene selezionando Simplify.
Per le matrici quadrate si calcola il determinante e la traccia (somma degli elementi diagonali) con
le funzioni Det e Trace:
Data una matrice M e un vettore v si possono calcolare i prodotti M.v e v.M (si noti che il simbolo
usato per questa operazione è il punto).
Nel primo caso si moltiplicano scalarmente le righe della matrice per il vettore, nel secondo le
colonne della matrice per il vettore.
[[a,b],[c,d]] . [2,3]
3
Scheda n. 10 – Vettori e matrici. Pag.
DERIVE calcola il prodotto di due matrici M ed N (sempre indicato con il punto .) purchè il numero
di colonne della prima matrice sia uguale al numero di righe della seconda.
L'elevamento alla potenza n di una matrice indica il prodotto della matrice per se stessa n volte:
Per calcolare l'inversa di matrici non singolari si eleva alla potenza n = -1.
Nel caso di matrici singolari, l'inversa non può essere calcolata e viene riscritta la matrice (linea #
24).
4
Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
11 – EQUAZIONI E DISEQUAZIONI: LA
“Introduzione a DERIVE” MODALITA’ EXACT
Con DERIVE si possono trattare equazioni e disequazioni (che chiamiamo con il termine generico
di relazioni). Per introdurle si usano gli operatori =, /= (diverso), < , <=, >, >=.
La soluzione di equazioni e disequazioni puo` essere fatta sia manualmente (imitando i passaggi
fatti a mano) sia automaticamente, tramite il comando Solve.
Premettiamo che il comando Simplify può essere applicato a una relazione e agisce
indipendentemente sui due membri. Allo stesso modo si comporta il comando Factor.
LA SOLUZIONE MANUALE DI UNA RELAZIONE
Il procedimento di soluzione manuale è utile per introdurre i metodi risolutivi delle equazioni e
inoltre deve essere utilizzato nei casi più complicati, in particolare quelli non lineari.
Supponiamo di dovere risolvere la disequazione 3x + 4 < 9. Dopo averla "scritta" nella linea di
editing selezionando Author e dopo aver confermato con OK, evidenziamola con il cursore
luminoso, selezioniamo ancora Author e battiamo il tasto funzione F4; la relazione viene riscritta
tra parentesi nella linea di editing.
Digitiamo ora –4 e confermiamo con OK. Sullo schermo appare:
(3*x+4<9)-4.
Selezioniamo Simplify
Procedendo in modo analogo dividiamo ambo i membri per 3 e arriviamo a
(3*x<5)/3
che sarà semplificato in
x<5/3.
Nel caso di coefficienti letterali, possiamo procedere in modo del tutto analogo per le equazioni: per
risolvere l’equazione
a*x+1=a/(a+1)
sottraiamo 1 ad ambo i membri, dividiamo per a (per a 0):
Scheda n. 11 – Equazioni e disequazioni: la modalità Exact. Pag.
Nella corrispondente disequazione
a*x+1<a/(a+1)
il primo passaggio e` identico, mentre DERIVE non esegue (ovviamente!) la divisione per a (la
linea #15 è il risultato della semplificazione della linea #14):
Dichiarando il dominio di a (e quindi il suo segno) come visto nel Capitolo 8 otteniamo il risultato
desiderato:
Le linee #17 e #19 rappresentano il risultato della semplificazione della precedente linea #14 dopo
le dichiarazioni di a come variabile, rispettivamente positiva e negativa.
2
Scheda n. 11 – Equazioni e disequazioni: la modalità Exact. Pag.
3
LA SOLUZIONE AUTOMATICA DI UNA RELAZIONE
Una relazione può essere risolta con il comando Solve, disponibile nel menu (e anche nella barra
degli strumenti), oppure con la funzione SOLVE(relazione,variabile) digitata nella linea
di editing.
Le modalità di soluzione sono completamente diverse a seconda che si lavori in modalità Exact
oppure Approximate.
Esaminiamo la modalita` Exact.
EQUAZIONI ALGEBRICHE IN UNA INCOGNITA
Esistono vari modi per ottenere la soluzione di una equazione; qui ora mostreremo la digitazione
diretta nella linea di editing dopo aver selezionato Author. Si noti che la funzione Solve richiede
come primo argomento la relazione e come secondo argomento la variabile rispetto alla quale si
desidera risolverla. Selezionando Simplify si ottiene il risultato. Si noti che la soluzione è racchiusa
tra parentesi quadre: ciò significa che le soluzioni sono presentate sotto forma di vettore.
Solve riconosce equazioni impossibili restituendo un “vettore vuoto”: [ ]; per quelle indeterminate
la soluzione e` scritta nella forma x=@1. Il simbolo @ deve essere letto come `costante arbitraria'; il
numero seguente viene aggiornato e aumentato di uno ogni volta che interviene una nuova costante
arbitraria.
Se si usa la modalità Exact, il comando Solve cerca tutte le possibili soluzioni COMPLESSE
dell'equazione INDIPENDENTEMENTE dal fatto che l'incognita sia stata dichiarata in un altro
dominio.
Vengono risolte le equazioni di grado 2, 3 e 4, le equazioni di grado superiore che possono essere
fattorizzate o ridotte a equazioni di questo tipo.
Valgono a proposito di Solve tutte le osservazioni viste a proposito di Factor, riguardo al fatto che
equazioni di grado superiore al quarto non sono risolte (in generale) e che le soluzioni di equazioni
di terzo e di quarto grado possono essere scritte con radicali doppi o funzioni trigonometriche
inverse in modo scarsamente leggibile e utile.
DERIVE risolve, con le stesse limitazioni, anche le disequazioni:
Scheda n. 11 – Equazioni e disequazioni: la modalità Exact. Pag.
4
Il polinomio seguente è uguale a (x-1)^2*(x^2+1); si osservi la “furbizia” di DERIVE:
Sono risolte anche l'equazione e la disequazione `fondamentale' con il valore assoluto avente
argomento lineare in x:
mentre talvolta non sono risolte disequazioni di poco più complicate o con argomenti del modulo
non lineari:
Nel precedente capitolo abbiamo sempre operato impartendo il comando Solve direttamente da
tastiera. Un altro modo per impartire il comando è usare il menu Solve selezionando l’opzione
Algebraically. Si apre così una finestra di dialogo con una linea di editing nella quale, se è stata
evidenziata un’equazione, questa è automaticamente inserita, oppure può essere digitata l’equazione
desiderata. Nel campo Variable selezionare, se necessario, l’incognita desiderata (vengono
presentate tutte le variabili presenti nell’equazione) e infine selezionare OK.
Scheda n. 11 – Equazioni e disequazioni: la modalità Exact. Pag.
Selezionare infine Simplify.
5
Corso di aggiornamento “Algebra tra tradizione e rinnovamento”
Prof. Paolo Boieri
12 – EQUAZIONI E DISEQUAZIONI:
“Introduzione a DERIVE” LA MODALITA’ APPROXIMATE
In questo file è necessario utilizzare la modalità approssimata che, come noto, si attiva dal menu
Declare, Algebra State, Simplification, selezionando Approximate nel campo Precision Mode
oppure attivando la linea di editing con il comando Author e digitando:
Precision:=Approximate.
In alternativa per risolvere le equazioni in modalità Approximate si può usare il menu Solve come
visto al termine del Capitolo precedente e selezionando Numerically.
EQUAZIONI IN UNA INCOGNITA
Se si usa la modalità Approximate viene cercata una soluzione approssimata REALE
dell'equazione (o della disequazione).
E` spesso utile iniziare tracciando il grafico della funzione, per vedere se esiste una soluzione
dell'equazione e per avere un'idea dell'intervallo in cui si trova. Se si usa Solve da menu viene
richiesto di scegliere l'intervallo in cui cercare la soluzione (Bounds = Estremi, Lower = Inferiore,
Upper = Superiore) , mentre con la funzione SOLVE digitata direttamente questo non è necessario.
Tuttavia è possibile aggiungere gli estremi dell'intervallo come terzo e quarto argomento di questa
funzione.
Vediamo alcuni esempi.
Questo polinomio ha una sola radice reale:
Scheda n. 12 – Equazioni e disequazioni: la modalità Approximate. Pag.
2
Questa equazione ha invece tre radici reali:
x5 – 7x + 5 = 0.
Scegliendo l'intervallo di default [10,10] si ottiene x = 1.77041, mentre in [0,10] si ha x =
1.34642. L'altra soluzione viene individuata scegliendo l'intervallo [0,1]: x = 0.747661:
DERIVE usa una variante del metodo di bisezione; si osservi che il procedimento non si arresta se la
funzione ha lo stesso segno agli estremi (vedi l'ultimo esempio con estremi 0 e 10).
Nel caso in cui esistano più soluzioni nell'intervallo indicato, non è facilmente prevedibile quale
radice viene trovata.
La soluzione approssimata è l'unica possibile per equazioni che contengono funzioni algebriche e
trascendenti.