Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Strumenti per la Misura di Grandezze Elettriche
Introduzione
Gli strumenti elettromeccanici possono essere schematicamente rappresentati da un
organo mobile sul quale agisce una coppia motrice Cm, la quale comporta una rotazione di
un angolo δ dello stesso, ed alla quale si oppone una coppia antagonista Ca, sino al
raggiungimento di una condizione di equilibrio tra le due coppie. Detta x la grandezza
elettrica che ha determinato lo spostamento angolare dell'organo mobile e δ lo
spostamento angolare corrispondente, la condizione di equilibrio è
C (x) = C (δ)
Volendo tener conto degli attriti, l'equazione fondamentale l'equilibrio degli strumenti
elettromeccanici deve scriversi
C (x) = C (δ) ± C
dove Cr è la coppia resistente dovuta agli attriti, la quale dipende dalla più o meno buona
realizzazione costruttiva dei perni sui quali è montato l'equipaggio, mobile. Tale coppia
resistente cresce al crescere del peso dell'equipaggio mobile e può, per ogni strumento,
ritenersi costante. Il doppio segno tiene conto del fatto che la coppia di attrito non ha un
segno proprio ma si oppone sempre al movimento.
Tramite la condizione di equilibrio si ha un legame tra la grandezza x, in ingresso, e la
conseguente deviazione δ dell'organo mobile. Collegando all'organo mobile un indice, si
ha l'indicazione corrispondente all'entità della grandezza da misurare. Gli strumenti si
classificano in base alla relazione che lega Cm con x.
A seconda del tipo di interazione che fa nascere la coppia motrice si ottengono diverse
famiglie di strumenti, ognuna con il suo campo di applicazione ed in particolare, interazioni
tra correnti (strumenti elettrodinamici), interazioni tra una corrente ed un campo magnetico
(strumenti magnetoelettrici o a bobina mobile ed elettromagnetici o a ferro mobile),
interazioni tra conduttori carichi (strumenti elettrostatici) ed interazioni tra correnti indotte
su di un materiale conduttore (strumenti ad induzione). Gli strumenti magnetoelettrici sono
utilizzabili solo per misure in corrente continua, gli strumenti elettromagnetici,
elettrodinamici ed elettrostatici possono essere utilizzati sia in continua sia in alternata,
mentre gli strumenti ad induzione funzionano solo in corrente alternata.
In generale, per valutare la coppia motrice si può far ricorso ad un metodo di carattere
energetico, il quale viene quasi sempre preferito, non essendo l'unico, per la sua rapidità.
Nel caso di circuiti elettrici nei quali sia immagazzinata energia magnetica, la coppia
motrice agente su ogni circuito può calcolarsi valutando la variazione di energia magnetica
relativa ad una variazione elementare dello spostamento angolare δ
C =
dΕ
dδ
1
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Gli strumenti per la misura di una tensione e di una corrente elettrica sono chiamati,
rispettivamente, voltmetri ed amperometri. Un amperometro deve sempre essere inserito
in serie al circuito del quale si vuole misurare l’intensità di corrente. Esso deve perciò
avere la minima resistenza R possibile, sia per rendere minima la caduta di tensione
provocata dall’apparecchio - affinché la sua inserzione alteri il meno possibile le condizioni
del circuito – sia per rendere minima la potenza in esso dissipata. Dualmente, per le
stesse due ragioni, un voltmetro, che deve essere messo in derivazione tra i due punti del
circuito di cui si vuole misurare la differenza di potenziale, deve avere una resistenza
interna quanto più grande possibile.
Strumenti Magnetoelettrici
In questo tipo di strumenti, la coppia motrice è proporzionale alla grandezza elettrica in
ingresso
C = k∙x
Essi sono quindi detti "equipaggi ad azione proporzionale" caratterizzati da scala uniforme.
Questi strumenti sono chiamati comunemente "a bobina mobile" e sono basati sull'azione
motrice esercitata dal campo di un magnete permanente (parte attiva) su una bobina
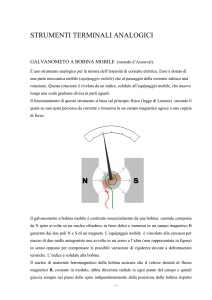
percorsa da una corrente continua. Secondo la disposizione più comune, uno strumento di
tale tipo è essenzialmente costituito da una bobinetta, di solito rettangolare e con un
numero n di spire, portata da un asse a perni ruotanti, come illustrato in Fig. 1. In genere,
per ridurre il valore della coppia resistente, i perni cilindrici, in alluminio, hanno la punta
riportata in acciaio indurito a forma conica e sono levigati a sfera nella parte terminale.
Due molle a spirale servono a portare la corrente alla bobina mobile ed a fornire la coppia
antagonista individuando la posizione normale di riposo dell'indice. I lati della bobina
paralleli all'asse, lati attivi, si trovano nei traferri esistenti fra le espansioni polari, N e S, di
un magnete ed un nucleo, o toro centrale, di ferro dolce.
Nel caso di un campo magnetico rettilineo ed uniforme di induzione B, con la bobina piana
di n spire e di area S=D∙l, misurando gli angoli dell'asse del campo, il flusso concatenato
risulta Φ = nBDlsenδ, con Dlsenδ pari all' area interessata dal flusso stesso.
L'energia magnetica associata al sistema è E = Φ ∙ i e la coppia motrice risulta
C =
dΕ
1
= i ∙ nBDlcosδ
dδ
2
Per avere uno strumento a scala proporzionale deve essere k=nBDlcosδ=cost. Ciò si
ottiene mediante una forma opportuna delle espansioni polari in modo da avere, su tutta la
zona in cui si può muovere la bobina, un campo di induzione B costante e di direzione
radiale, come mostrato in Fig. 1.
In questo caso il flusso concatenato è Φc=nBDδl con Dδl area interessata dal flusso e D
arco di circonferenza sotteso al flusso. L'energia magnetica associata al sistema è
Em=Φc∙i=nBDδl∙i e la coppia motrice risulta
2
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
C =
dΕ
1
= i ∙ nBDl
dδ
2
con k=nBDl=cost la coppia motrice diventa
C = k∙i
Fig. 1
Lo strumento magnetoelettrico è intrinsecamente un milliamperometro con un limite
superiore di portata di circa 100mA e limite inferiore di qualche µA. Per passare da un
milliamperometro ad un millivoltmetro occorre inserire una rete di resistenze tale che
R =
U
I
In modo da avere una relazione univoca tra la tensione U applicata ai morsetti di ingresso
e la deviazione dell’indice dello strumento.
Questi strumenti possono essere correntemente costruiti in classe 0.2 e si arriva fino a
strumenti di classe 0.1, tali cioè che, ad esempio, per un voltmetro da 100 V di fondo scala
non si abbia in nessun punto della scala un errore assoluto superiore a 0.1V. Essi sono
inoltre caratterizzati da bassi consumi essendo la potenza necessaria a mandare a fondo
scala uno strumento di questo tipo, dell'ordine di 10-4 ÷ 10-6 W.
Gli strumenti magnetoelettrici hanno il pregio di un ottimo smorzamento elettromagnetico,
prodotto dalle correnti indotte nel telaietto metallico, sul quale è avvolta la bobina mobile, e
dalle correnti indotte sulla stessa bobina. Nella bobina infatti nasce una forza
elettromotrice (ritenendo il campo radiale ed uniforme ed essendo ω la velocità angolare
nell'istante considerato) e=k1B∙ω.
Se la bobina fa parte di un circuito chiuso di resistenza complessiva R, si ha una corrente
=
e k Bω
=
R
R
che, per la legge di Lenz, frena il movimento.
Vediamo ora come, sia pure con i valori limitati di corrente ammessi nell'interno della
bobina mobile e delle molle, si possono misurare correnti e tensioni maggiori.
3
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Amperometro
Mettendo in parallelo al milliamperometro un derivatore di resistenza R, come mostrato in
Fig. 2, ed inserendo questo sistema in serie al circuito di cui si vuole misurare la corrente I,
si ha che
∙ = R(I − i) = RI − Ri
=
r+R
∙i =m∙i
R
con m definito Potere Moltiplicatore dello Shunt
Fig. 2
Volendo misurare una corrente I, disponendo di uno strumento con portata i0, si ha
=m=
r+R
R
da cui si ricava, nota la r propria dello strumento, il valore R della resistenza da inserire in
parallelo allo strumento stesso
R=
r
m−1
In questo modo lo strumento è attraversato solo da una parte della corrente I. Il valore
della lettura deve essere poi moltiplicato per m per avere il valore della corrente I. Con
questo metodo si possono misurare correnti fino a 20000 ÷25000 A.
Voltmetro
Mettendo in serie allo strumento, di portata i0 e di resistenza interna r un resistore
addizionale R come in Fig. 3, si ha
I=
U
R+r
e quindi
C =k∙i =
k
∙U= k ∙U
R+r
4
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Lo strumento, la cui scala può essere tarata direttamente in Volt, diventa un voltmetro di
portata V0=(R+r)∙i0
Fig. 3
Strumenti Elettrodinamici
Caratteristiche Costruttive e di Funzionamento
L'elettrodinamico è uno strumento nel quale la coppia motrice è proporzionale al prodotto
di due grandezze in ingresso. Questo tipo di strumento è costituito, nella sua forma più
semplice, da due bobine in aria, una interna all'altra; la bobina interna è mobile rispetto
all'altra che è fissa e ad essa è in genere collegato un indice, come illustrato in Fig. 4.
Fig. 4
Per ottenere una buona sensibilità dello strumento, la bobina mobile è attraversata dalla
corrente im ed ha peso e sezione minori della bobina fissa attraversata dalla corrente if.
L'energia magnetica immagazzinata è
1
1
E = L i + L i + Mi i 2
2
con Lm e Lf coefficienti di autoinduzione delle due bobine e M coefficiente di mutua
induzione tra bobina fissa e bobina mobile. Derivando l'espressione dell'energia magnetica
5
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
rispetto allo spostamento angolare α della bobina mobile, mantenendo costanti le correnti,
l’unico parametro che varia è M
C =
dE
dM
=ii
dα
dα
Affinché la coppia motrice sia proporzionale al prodotto delle correnti, occorre che M vari
in modo lineare con l'angolo di deviazione, in maniera che risulti
dM
= k = cost
dα
In particolare, prendendo in esame l'andamento di M in funzione di α che è rappresentato
da una cosinusoide, esiste solo un intervallo all'interno del quale si può ritenere che
l'andamento di M con α è di tipo lineare. Tale intervallo è di circa 45° intorno a 90°. Quindi
limitando l'escursione di α in tale intervallo si può avere
C =k∙i i
Lo strumento elettrodinamico può essere usato sia in corrente continua sia in corrente
alternata. Se la corrente è continua, risulta
C = k∙I I
Se le correnti sono alternate, di valore efficace Im e If,
i = √2I ∙ senωt
i = √2I ∙ sen(ωt + β)
la coppia motrice vale
C = k ∙ 2I I sen(ωt)sen(ωt + β)
C = k ∙ I I cosβ − k ∙ I I cos(2ωt + β)
Quindi, nel caso di correnti sinusoidali, la coppia è data dalla somma di due termini, uno
costante e l'altro variabile con una pulsazione doppia. Se l'equipaggio mobile ha un'inerzia
elevata o una pulsazione caratteristica minore della pulsazione ω, lo strumento segna
un'indicazione proporzionale solo alla coppia media, pari al termine costante della
precedente espressione.
Se lo strumento è in aria si hanno coppie inferiori e consumi più elevati rispetto agli
strumenti magnetoelettrici. La costante k dipende tuttavia solo dalla geometria delle
bobine ed assicura perciò, alla precisione dello strumento, una buona permanenza nel
tempo. Il funzionamento di questo strumento non dipende dalla frequenza almeno finchè il
valore di M non sia influenzato dalle correnti indotte in parti metalliche adiacenti le bobine.
Lo strumento è invece sensibile ai campi magnetici di origine esterna, isofrequenziali con
la corrente im. In questo caso si possono adottare diverse soluzioni; si possono introdurre
schermi magnetici,
6
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
si possono impiegare strumenti ferroelettrodinamici che sono in pratica strumenti
elettrodinamici nei quali la bobina fissa è avvolta su materiale ferromagnetico, si può
ricorrere a strumenti astatici.
Milliamperometro Elettrodinamico
La bobina mobile, e quella fissa si dispongono in serie come da Fig. 5. Poiché la corrente
è unica si ha I=Im=If. La coppia motrice risulta, in corrente continua, pari a Cm=kI2 e, in
corrente alternata, pari a Cm=kIeff2 e quindi lo strumento misura direttamente il valore
efficace.
Relativamente ai valori di portata, il limite inferiore è fissato dalla necessità di mantenere
ad un determinato valore il rapporto coppia/peso. In particolare, nel caso degli strumenti
elettrodinamici, bobina fissa e mobile sono in aria, si hanno campi magnetici di piccola
entità e quindi coppie motrici deboli. Quindi, per un fissato, rapporto coppia/peso, al
diminuire della corrente occorrerebbe incrementare il campo magnetico mediante un
aumento del numero di spire della bobina con conseguente aumento di peso della bobina
mobile. I limiti superiori di portata sono imposti dalle necessità di limitare il riscaldamento
delle molle attraverso le quali passa la corrente. Conseguentemente, il valore massimo di
corrente ammissibile da questi milliamperometri è di circa 0.2A. Il campo di impiego di
questi strumenti si estende circa da 10mA a 100mA.
Fig. 5
Voltmetri Elettrodinamici
Nel caso di impiego dello strumento elettrodinamico come voltmetro, si mette in serie alle
bobine una resistenza addizionale indipendente dalla temperatura (Fig. 6). Abbiamo visto
che l'espressione della coppia motrice per questi strumenti è
C = k ∙ I I cosβ
Nel caso del voltmetro si ha
I =I =
e β=0
con Z modulo dell’impedenza complessiva del circuito. La coppia motrice in corrente
continua è
7
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
C = kI = k
U
=kU
R
dove R è la serie della resistenza addizionale con le resistenze delle due bobine. In
corrente alternata si ha invece
C = kI = k
U
U
k
=k
=
∙
Z
R +X
R
1
X
1+
R
=k U
la costante k" in corrente alternata è la stessa del caso in corrente continua solo se
X
ω L
≪ 1, quindi
≪1
R
R
con L=Lf+Lm. Ciò limita l'impiego dello strumento ad un range di frequenza di 10÷1000Hz.
Questi voltmetri non si costruiscono per portate inferiori a 30÷100V in quanto, il consumo,
raramente inferiore alle decine di mA, sarebbe eccessivo. Salendo con i valori di portata,
cresce corrispondentemente la potenza dissipata nel resistore addizionale.
Fig. 6
Amperometri elettrodinamici
La bobina mobile e la bobina fissa si dispongono in parallelo, mentre in serie ad ognuna di
esse si pone unaresistenza che chiamiamo Rf per la bobina fissa e Rm, per quella mobile,
così come indicato in Fig. 7. Queste resistenze sono tali da ripartire la corrente I da
misurare tra le due bobine in modo che la quota Im, che percorre la bobina mobile, non
superi il limite imposto dal riscaldamento. Ciò consente di aumentare la portata dello
strumento fino a decine di ampere. In corrente continua risulta If∙Rf=Im∙Rm e poichè Rm>>Rf
I
R
=
=α≫1
I
R
essendo =
+
=
I
8
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
C =k∙I I =k∙I
I
k
α
= I =k
I
(α + 1)
α α
In corrente alternata, dette Rm, Xm, Zm, Rf, Xf, Zf rispettivamente resistenza, reattanza e
impedenza delle due bobine, la corrente totale da misurare I si scompone in due
componenti Im e If tali che Ż I ̇ = Z ̇ I ̇ e quindi
İ
Ż
R + jX
=
=
̇
̇
R + jX
I
Z
X
R 1+ jR
=
R 1+jX
R
Da tale espressione si evince che il rapporto tra le correnti è ancora uguale a quello tra le
resistenze solo se
X
X
=
R
R
In tal modo il rapporto tra le correnti If e Im e la loro concordanza in fase, vengono
conservati indipendentemente dalla frequenza. La precedente condizione è però vera solo
in prima approssimazione in quanto si deve tener conto della mutua induzione tra le
bobine. Per ritrovare la stessa condizione che si ha in corrente continua dovrebbe
realizzarsi l'uguaglianza
L −M L −M
=
R
R
Questa uguaglianza è impossibile, essendo M variabile con la posizione dell'equipaggio
mobile. Si può dimostrare che questo comporta un errore che cresce con il quadrato della
frequenza e che, dipendendo dal segno di M, è positivo all'inizio della scala e negativo
verso il fondo scala. E' questo errore che limita l'impiego degli amperometri elettrodinamici
in corrente alternata ad un range di frequenza di 10÷1000Hz.
Fig. 7
Wattmetro Elettrodinamico
Il wattmetro elettrodinamico è costituito da una bobina fissa F (bobina amperometrica),
posta in serie al carico da misurare e da una piccola bobina mobile M (bobina voltmetrica),
che viene collegata in parallelo, mediante una grossa resistenza addizionale Ra, ai capi
del carico, in modo da condividere la medesima differenza di potenziale ed essere
9
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
percorsa da una debole corrente a essa proporzionale. Il wattmetro è caratterizzato da
una portata amperometrica, che rappresenta la massima corrente che può attraversare la
bobina amperometrica e da una portata voltmetrica, che rappresenta la massima tensione
applicabile ai capi della bobina voltmetrica. Il prodotto di queste due portate dà la portata
wattmetrica (potenza massima misurabile). Lo schema di principio e di inserzione è
mostrato in Fig. 8.
Fig. 8
L’impedenza ZV della bobina voltmetrica M è data da
Z =
R +X
La resistenza della bobina voltmetrica RM è grande rispetto alla reattanza XV della bobina
mobile M in quanto la bobina M è costituita da un conduttore di piccola sezione e con un
grande numero di spire (XV<RM). La resistenza complessiva del circuito voltmetrico, è data
dalla somma di Ra più la resistenza propria della bobina RM, RV=(Ra+RM)>>XV, la XV quindi
risulta trascurabile rispetto alla resistenza totale del circuito voltmetrico RV pertanto
l’impedenza della bobina volumetrica ZV, si può ritenere pari alla RV.
Per tale motivo la tensione U e la corrente IV circolante nella bobina voltmetrica si possono
considerare in fase e la IV è data da
I =
U
R
Nel circuito amperometrico la corrente I è la stessa di quella di linea, in quanto la bobina
amperometrica è costituita da poche spire di grossa sezione e presenta quindi, sia una
reattanza XA che una resistenza RA molto piccole e quindi trascurabili. Pertanto lo
sfasamento φ presente fra la tensione e corrente in linea è lo stesso di quello presente fra
la IV e la I nel wattmetro e quindi la coppia media che risulta proporzionale al prodotto dei
valori efficaci delle correnti per il coseno dell'angolo φ fra di essi compreso
C = k ∙ II cosφ
dove cosφ rappresenta il fattore di potenza della linea e poiché I =
C =k∙I
si ha
U
cosφ = k ∙ P
R
con P = UIcosφ
10
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Strumenti Elettromagnetici
Gli strumenti a ferro mobile sono costituiti da una bobina fissa (di molte spire) e da un
equipaggio mobile sul quale è predisposto del materiale ferromagnetico, in grado di
ruotare all’interno della bobina. Essi sono prevalentemente usati in quelle applicazioni in
cui la robustezza è preferita all’elevato grado di precisione. Esistono diverse realizzazioni
di strumenti a ferro mobile, due delle quali sono riportate nella Fig. 9.
Fig. 9
In Fig. 9a è riportata la realizzazione ad attrazione (o anche a succhiamento), mentre in
Fig. 9b è riportata la realizzazione a repulsione. In entrambi i casi, si nota la presenza del
solito indice solidale con l’equipaggio mobile e delle solite molle antagoniste. Per quanto
riguarda, invece, lo smorzamento, è ottenuto per via elettromagnetica.
Vediamo di comprendere il funzionamento di uno strumento di questo tipo. Consideriamo,
in particolare, la realizzazione ad attrazione. Sia I la corrente continua o il valore efficace
della corrente alternata che scorre nella bobina fissa; a causa di questa corrente, il ferro
tende ad essere risucchiato (da cui il nome) all’interno della bobina, fin tanto che risulti
massima l’energia immagazzinata nel campo magnetico. Tale energia vale E = LI
dove L è l’induttanza della bobina. La corrispondente coppia motrice è allora
C =
dE
1 dL
= I
dδ
2 dδ
Abbiamo dunque una proporzionalità diretta della coppia motrice sia con l’intensità di
corrente circolante sia con la legge di variazione di L. Tale variazione, dovuta appunto alla
penetrazione del ferro nella bobina, viene resa costante tramite una scelta opportuna della
forma e della posizione del ferro mobile rispetto alla bobina. Si realizza dunque la
condizione dL/dδ=2k da cui consegue che la coppia motrice è direttamente proporzionale
al quadrato dell’intensità di corrente
C = kI
Questa coppia è ovviamente equilibrata dalla “solita” coppia antagonista, proporzionale
alla deflessione secondo la legge Ca=Mδ. In condizioni di equilibrio, lo spostamento
dell’indice sulla scala graduata è proporzionale al quadrato della corrente che attraversa la
bobina fissa.
11
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Quando lo strumento è interessato da una corrente alternata, data la presenza
dell’equipaggio mobile (il quale possiede un momento di inerzia ed un proprio periodo di
oscillazione), l’equilibrio tra coppia motrice e coppia antagonista è tale che la deviazione
angolare sia proporzionale, come negli altri strumenti indicatori elettromeccanici, al valor
medio (sul periodo) della coppia motrice.
Consideriamo adesso uno strumento a ferro mobile del tipo a repulsione, rappresentato in
Fig. 9b. In questo caso, abbiamo una bobina fissa e due pezzi di materiale magnetico, di
cui uno solidale con la bobina fissa e l’altro in grado di ruotare. Il campo magnetico è
generato dalla circolazione della corrente I nella bobina; esso magnetizza nello stesso
modo i due pezzi di ferro, che quindi tendono a ruotare uno rispetto all’altro. Per quanto
riguarda le equazioni matematiche, valgono le stesse viste nel caso ad attrazione.
L’accuratezza degli strumenti a ferro mobile è limitata essenzialmente dalla curva di
magnetizzazione del ferro; questo comporta, tra le altre cose, che non sempre può
ritenersi valida la taratura in corrente continua per utilizzazioni in corrente alternata. Ci
sono poi ulteriori cause di errore, ad esempio legate agli attriti, al riscaldamento,
all’influenza di campi magnetici esterni, a fenomeni di isteresi, alle correnti parassite. Così
come negli strumenti elettrodinamici, la sensibilità è bassa, in quanto l’induzione
magnetica è creata da una bobina in aria attraversata da corrente. Un vantaggio, invece,
rispetto agli strumenti elettromeccanici, è nell’assenza di circuiti elettrici interessati dal
passaggio di corrente sull’equipaggio mobile. Lo strumento risulta perciò robusto ed in
grado di sopportare sovraccarichi elettrici. Sono bassi anche i costi (data la semplicità
costruttiva dell’equipaggio mobile) e lo strumento è meno danneggiabile da urti o
eccessive sollecitazioni meccaniche. Anche in questo caso, basta aggiungere derivatori e
resistori addizionali per ottenere strumenti (amperometri e voltmetri) a portate multiple. A
causa delle diverse cause di errore, questi strumenti sono usati in un ristretto campo di
frequenza (25-125 Hz) e per grandezze alternate sinusoidali.
Contatore a Induzione
Il contatore ad induzione, la cui struttura è schematicamente riportata in Fig. 10, è
costituito da un leggero disco di rame o di alluminio (D) calettato su un albero. Il bordo del
disco passa nei traferri di due elettromagneti posti generalmente l’uno vicino all’altro. Un
elettromagnete è detto amperometrico (EA) ed è eccitato con la stessa corrente I del
circuito. L’altro è detto elettromagnete voltmetrico (EV), ha l’avvolgimento di molte spire di
filo sottile, ed è collegato in derivazione sulla linea di alimentazione, risultando pertanto
alimentato dalla tensione U.
La corrente che percorre l’avvolgimento voltmetrico è indicata con IV. Un magnete
permanente (M) con funzione di freno abbraccia il disco. I due elettromagneti, eccitati dalle
correnti alternate I e IV di uguale frequenza e generalmente sfasate tra loro, generano i
flussi magnetici ΦA e ΦV, i quali attraversano il disco. Tali flussi inducono nel disco forze
12
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
elettromotrici ad essi proporzionali e sfasate in ritardo di 90° rispetto ai flussi stessi. Tali
forze elettromotrici a loro volta generano, nel disco, le correnti I1 e I2.
Fig. 10
Fig. 11
Come illustrato in Fig. 11, la corrente I2 con il flusso ΦA produce nel disco azioni
elettrodinamiche F1 agenti nel piano del disco stesso. Lo stesso avviene per la corrente I1
interagente con il flusso ΦV, che sviluppa la forza F2. Il disco è quindi sollecitato a girare in
senso contrario dalle due forze F1 e F2; esso è cioè sottoposto ad una coppia motrice Cm
proporzionale alla differenza F1-F2. Dalla teoria dello strumento ad induzione, come
mostrato più avanti, si ricava che la coppia motrice è proporzionale alle intensità dei due
flussi ΦA e ΦV ed al seno del loro angolo di sfasamento
C ∝ Φ Φ senβ
13
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Per effetto di tale coppia motrice il disco ruota. La velocità di rotazione del disco Ω è tale
per cui le correnti indotte nel disco dal magnete permanente danno luogo ad una coppia
frenante Cr, proporzionale alla velocità di rotazione stessa. All’equilibrio si ha, in prima
approssimazione, Cm=Cr.
Si vuole dimostrare che la coppia motrice Cm è proporzionale alla potenza attiva Cm∝P. Si
supponga inizialmente che l’elettromagnete amperometrico generi un flusso magnetico
ΦA, proporzionale alla corrente di linea I, isofrequenziale e in fase con essa. Come
illustrato in Fig. 12, il flusso ΦA che attraversa il disco induce in esso una forza
elettromotrice indotta E1 sfasata di 90° in ritardo, data da
E ̇ = −jωΦ
Tale forza elettromotrice produce nel disco stesso, che è assimilabile agli effetti elettrici ad
una spira di resistenza R e reattanza X, una corrente indotta I1, la cui espressione
fasoriale è
İ =
Ė
−jωΦ
=
R + jX
R + jX
Detto γ l’angolo di sfasamento tra il vettore della f.e.m. indotta E1 e quello della corrente
indotta I1, tale angolo è legato alle caratteristiche elettriche del disco dall’espressione
cosγ =
R
√R + X
2
Fig. 12
Fig. 13
Si supponga ora che l’elettromagnete voltmetrico generi un flusso magnetico ΦB,
proporzionale ed isofrequenziale alla tensione di linea U, ma sfasato rispetto ad essa di
90° in ritardo, come mostrato in Fig. 13. Il flusso ΦB risulta pertanto sfasato, rispetto al
flusso ΦA generato dall’elettromagnete amperometrico, di un angolo β=90°- dove è
l’angolo di fase tra la tensione e la corrente di linea. Il flusso ΦB che attraversa il disco
induce in esso una f.e.m. indotta E2, legata a ΦB dalla relazione fasoriale
E ̇ = −jωΦ
14
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Nel disco, per effetto dell’induzione prodotta dall’elettromagnete voltmetrico, circola quindi
la corrente indotta I2
İ =
Ė
−jωΦ
=
R + jX
R + jX
L’angolo di sfasamento tra il vettore della f.e.m. indotta E2 e quello della corrente indotta I2,
dipendendo solo dalle caratteristiche elettriche del disco, è ancora pari a γ. Ciascuna delle
due correnti indotte produce una coppia motrice per effetto del flusso prodotto dall’altro
elettromagnete. La corrente I1 col flusso ΦB sviluppa nel disco azioni elettrodinamiche
agenti nella direzione F1. La corrente I2 con il flusso ΦA sviluppa azioni elettrodinamiche
agenti nella direzione F2, come mostrato in Fig. 11. Per costruzione, F1 e F2 tendono ad
opporsi tra di loro, e pertanto il disco è sollecitato a ruotare in senso contrario dalle due
forze F1 e F2; esso è cioè sottoposto ad una coppia motrice proporzionale alla differenza
F1-F2.
La coppia istantanea risultante è pertanto proporzionale alla differenza delle due coppie
C ∝ Φ ( t) i ( t) − Φ ( t) i ( t)
Poiché le grandezze in esame sono sinusoidali, il valor medio Cm della coppia risulta
proporzionale a
C ∝ Φ I cos Φ I − Φ I cos Φ I
Dal diagramma fasoriale del contatore risulta Φ I = 90° + γ − β,Φ I = 90° + γ + β, da
cui deriva C = kΦ I cos(90° + γ − β) − kΦ I cos(90° + γ + β), dove si è indicato con k la
costante di proporzionalità. Poichè cos(90°+)=-sen, si ottiene
C = −kΦ I sen(γ − β) + kΦ I sen(γ + β)
Ricordando che cosγ = √
,
=√
,
=√
e sostituendo nell’espressione
della coppia media
C = kΦ
ωΦ
√R + X
C = kΦ Φ
sen(γ + β) − kΦ
ω
√R + X
C = kΦ Φ
C = kΦ Φ
√R + X
sen(γ − β)
[sen(γ + β) − sen(γ − β)]
ω
√R + X
ω
√R + X
C = 2k
ωΦ
2
2cosγsenβ
R
√R + X
senβ
ωR
Φ Φ senβ
R +X
cioè la coppia motrice risulta proporzionale all’intensità dei due flussi ΦA e ΦB ed al seno
dell’angolo tra essi compreso.
15
Applicazioni Industriali Elettriche – Strumenti per la Misura di Grandezze Elettriche
Dall’espressione della coppia media si deduce che affinchè la coppia motrice sia diversa
da zero i due flussi devono essere sfasati fra loro di un angolo β diverso da zero. Il
coefficiente di proporzionalità fra la coppia motrice e i due flussi A e B dipende dalla
pulsazione ω, dalla resistenza equivalente R e dalla reattanza equivalente X del disco. La
dipendenza dalla pulsazione indica che la coppia motrice è nulla a frequenza nulla; quindi
il contatore ad induzione non può essere impiegato per la misura dell’energia elettrica nei
sistemi funzionanti in corrente continua. La dipendenza dalla resistenza equivalente indica
che la coppia motrice dipende dalla temperatura, dal momento che la resistenza del disco
varia al variare della temperatura. Generalmente la reattanza equivalente del disco è
trascurabile rispetto alla sua resistenza, sicché il coefficiente di proporzionalità aumenta
con l’aumentare della frequenza e con il diminuire della temperatura.
Si riprenda ora l’espressione C = k Φ Φ senβ ricordando quali ipotesi hanno condotto a
tale espressione, il flusso ΦA è proporzionale alla corrente di linea I ed ha la sua stessa
frequenza e fase; il flusso ΦB è proporzionale alla tensione di linea U, con la stessa
frequenza e in ritardo di 90°. Queste ipotesi permettono di riscrivere la coppia motrice
come
C = k UIsen(90° − φ)
in quanto si è visto che vale la relazione β=90°- tra l’angolo di sfasamento tra I e U () e
l’angolo di sfasamento tra ΦA e ΦB (β). Si ottiene allora
C = k UIcosφ
ovvero, ricordando la definizione di potenza attiva in un sistema in regime alternato
sinusoidale Cm=k’’P. La coppia motrice è quindi proporzionale alla potenza attiva. Per
effetto di tale coppia, il disco ruota alla velocità angolare Ω. Ω è tale per cui le correnti
indotte nel disco stesso dal magnete permanente danno luogo ad una coppia frenante Cr
che all’equilibrio è uguale alla coppia motrice. Tale coppia frenante agente sul disco risulta
proporzionale alla velocità angolare Ω del disco stesso, Ω∝Cr. Il coefficiente di
proporzionalità dipende dalla resistività del disco e quindi dalla temperatura. Questo effetto
compensa in parte l’analogo effetto della temperatura sulla coppia motrice. Pertanto, in
prima approssimazione, si ottiene P∝Ω. Ricordando che l’energia misurata da un
contatore ad induzione è proporzionale al numero di giri effettuati dal disco, la condizione
P∝Ω è condizione necessaria e sufficiente perché un contagiri (che in questo caso ha la
funzione di integratore) comandato dall’asse stesso del disco, possa indicare direttamente
l’energia E che transita nella sezione del circuito in cui è inserito il contatore stesso.
Nei tradizionali contatori ad induzione il conteggio del numero di giri avviene
meccanicamente. L’estremità dell’albero del disco è munita di una vite senza fine tramite
la quale l’albero, mentre gira, mette in rotazione un piccolo pignone. Il pignone è collegato
ad un numeratore a rulli. Ad ogni giro completo del pignone, il numeratore aumenta di una
unità. Il contatore viene regolato in modo tale che 1000 giri del pignone corrispondano ad
1kWh di energia consumata.
16