Circuiti in corrente continua

UNIVERSITA’ DEGLI STUDI DI FIRENZE
Facoltà di Scienze M.F.N.
Corso di Laurea in Matematica
Prof. Andrea Stefanini
Appunti aggiuntivi al corso di
LABORATORIO DI FISICA 2
CIRCUITI IN CORRENTE CONTINUA
Anno Accademico 2009-2010
1
1
Introduzione
Si definisce circuito elettrico un insieme di elementi collegati tra loro allo scopo di
trasferire energia elettrica. Gli elementi ideali fondamentali che possono contribuire a
formare un circuito si dividono in due categorie: elementi passivi ed elementi attivi. Appartengono alla prima categoria quegli elementi, come i resistori, i condensatori e gli
induttori, che dissipano o immagazzinano energia. Fanno invece parte della seconda i
generatori di tensione e quelli di corrente che forniscono energia agli elementi passivi inseriti nei circuiti di cui fanno parte.
Il generatore ideale di tensione è una sorgente di energia capace di fornire ai propri
terminali una differenza di potenziale elettrico (d.d.p. nel seguito) costante indipendentemente dalla resistenza di carico che alimenta e quindi dall’intensità della corrente che
circola nel circuito.
Il generatore ideale di corrente è una sorgente di energia capace di erogare una corrente di intensità costante, indipendentemente dalla resistenza di carico che alimenta e
quindi dalla d.d.p. presente ai capi della resistenza.
Anche gli elementi passivi verranno considerati inizialmente come elementi ideali, (per
es. con il simbolo R indicheremo elementi puramente resistivi), facendo inoltre l’ipotesi
che essi non varino né con il tempo né con l’intensità dell’impulso di tensione o corrente
applicato. Tale schematizzazione ci permetterà di ottenere delle equazioni differenziali
lineari e a coefficienti costanti per la descrizione delle intensità di corrente e delle d.d.p.
nelle varie parti del circuito, semplificandone notevolmente la soluzione.
Presenteremo nel seguito le leggi fisiche principali valide nei circuiti in corrente continua.
2
La legge di Ohm
Se ai capi di un conduttore “ohmico” viene applicata una d.d.p. V , esso viene percorso
da una corrente di intensità I. Si può verificare sperimentalmente che al variare della
d.d.p. V il rapporto VI rimane costante. A questa costante, caratteristica della natura,
dello stato fisico e delle dimensioni del conduttore, si dà il nome di resistenza elettrica
e la si indica con R. La legge di Ohm può quindi essere espressa nella forma
V = RI
(1)
Se riportiamo in grafico la corrente I che percorre il conduttore in funzione della d.d.p. V
applicata ai suoi capi, ovvero rappresentiamo la relazione I = f (V ), otteniamo quella che
viene detta “la curva caratteristica” del conduttore. Per i conduttori ohmici tale curva è
una retta che passa per l’origine e la cui pendenza rappresenta l’inverso della resistenza R
(detta “conduttanza”). Un conduttore per cui vale tale curva caratteristica viene anche
detto “lineare” (essendo I ∝ V ) e “bilaterale”, nel senso che il suo comportamento non
dipende dal verso della corrente.
2
3
Le leggi di Kirchhoff
Una rete, ovvero un insieme di più circuiti collegati tra loro, contiene elementi circuitali
attivi e passivi ed è costituita dalla combinazione di due componenti (logici e fisici) base:
i nodi e le maglie. Per nodo si intende un punto in cui convergono più di due elementi;
per maglia si intende invece una successione chiusa di elementi che partendo da un nodo
permette di tornare ad esso attraversando ogni elemento solo una volta. Viene infine
indicato con il termine ramo l’insieme di elementi che collega un nodo ad uno dei nodi
adiacenti.
Prima legge
La somma algebrica delle correnti confluenti in un nodo di un circuito elettrico è sempre nulla. La somma algebrica si intende eseguita considerando positive le correnti che
entrano nel nodo e negative quelle che ne escono, o viceversa. Tale principio deriva dal
fatto che la quantità di carica elettrica che arriva al nodo in un certo intervallo di tempo
è uguale a quella che se ne allontana nello stesso intervallo di tempo; in caso contrario si
avrebbe infatti un accumulo o una perdita di carica nel nodo.
Seconda legge
Lungo una qualsiasi maglia di un circuito elettrico la somma algebrica delle cadute
ohmiche Rj Ij è uguale alla somma algebrica delle f.e.m. Vk eventualmente presenti nella
maglia stessa. Il secondo principio può essere espresso analiticamente dalla relazione
X
k
Vk =
X
Rj Ij
(2)
j
relazione che si ottiene fissando un verso positivo arbitrario di percorrenza della maglia e
considerando positive le cadute ohmiche associate ad una corrente di ramo concorde con il
verso prefissato; le f.e.m. positive sono quelle che vengono attraversate dal polo negativo
a quello positivo percorrendo la maglia nel senso positivo prefissato.
Questo principio consegue immediatamente dall’applicazione della legge di Ohm ai singoli
rami che costituiscono la maglia.
Basandosi sulle leggi di Kirchhoff è possibile scrivere un sistema di equazioni lineari
con almeno tante equazioni quante sono le incognite (correnti) del problema. In genere
le equazioni ricavabili sono in numero maggiore delle incognite, ma alcune delle equazioni
non sono indipendenti tra loro. Esistono procedure (ad es. il metodo delle correnti di
maglia) che permettono di ricavare solo le equazioni indipendenti e portano velocemente
alla soluzione del problema.
4
Applicazioni
Vediamo subito alcune applicazioni delle leggi sopra enunciate.
Circuito serie
Quando un certo numero di componenti elettrici sono collegati in un circuito in modo da
3
essere attraversati dalla stessa corrente si dice che sono disposti in serie. Consideriamo ad
esempio un circuito, come quello di Fig.1, costituito da un generatore di tensione con tre
resistori in serie. Applicando la legge di Ohm ai
capi delle tre resistenze si ha:
V1 = R1 I
V2 = R2 I
V3 = R3 I (3)
dove I è la corrente che circola nel circuito. Essendo V la tensione ai capi del generatore deve
risultare
V = V1 + V2 + V3
(4)
Dalle 3 e 4 si ottiene
Figura 1: Circuito serie
V = R1 I + R2 I + R3 I = (R1 + R2 + R3 )I = Req I
(5)
dove si è introdotta la resistenza equivalente Req pari alla somma delle resistenze connesse
in serie.
Circuito parallelo
Quando un certo numero di componenti elettrici sono collegati in un circuito in modo che
ad essi sia applicata la stessa d.d.p. si dice che sono disposti in parallelo. In Fig.2 è
riportato l’esempio di un circuito costituito da un generatore e da tre resistori in parallelo.
Indicando con V tale d.d.p., la corrente in
ogni resistore si ottiene mediante la legge di
Ohm
V
V
V
I1 =
I2 =
I3 =
(6)
R1
R2
R3
Indicando con I la corrente erogata dal
generatore, la prima legge di Kirchhoff ci dice
che
Figura 2: Circuito parallelo
I = I1 + I2 + I3
(7)
Introducendo le eq.5 nella eq.7 si ricava quindi
V
V
V
I=
+
+
=V
R1 R2 R3
1
1
1
+
+
R1 R2 R3
=
V
R
(8)
dove si è introdotta la resistenza equivalente R definita da
1
1
1
1
=
+
+
R
R1 R2 R3
(9)
cioè il reciproco della resistenza equivalente è uguale alla somma dei reciproci delle resistenza presenti nel circuito parallelo. Da tale definizione segue immediatamente che
la resistenza equivalente di un circuito costituito da un numero qualsiasi di resistori in
parallelo è sempre minore di ciascuna delle resistenze del circuito.
4
Rete
Una connessione di circuiti serie e parallelo si
chiama rete. L’esempio che segue mostra una
rete con un solo generatore nella quale, utilizzando le relazioni ottenute per i circuiti serie e parallelo, è possibile ricavare la resistenza equivalente
dell’intera rete vista ai capi del generatore. Nella
fig.3 sono riportati i singoli passaggi che permettono di arrivare alla relazione che definisce la resistenza equivalente. Lo studente è invitato a
seguirli e ad applicare la stessa procedura anche
per altre reti.
Figura 3: Rete
5
5
Il teorema di sovrapposizione
Se in un circuito lineare agiscono simultaneamente diversi generatori, la corrente totale
prodotta in un generico ramo è la somma delle correnti che sarebbero prodotte dai singoli
generatori se ciascuno di essi agisse isolatamente. Nel seguito è riportato un esempio di
una rete con due generatori di tensione alla quale l’applicazione del teorema permette
velocemente di determinare la corrente che scorre sulla resistenza R3 . Nell’esempio la
Figura 4:
corrente che scorre in R3 viene determinata come somma delle correnti prodotte su R3
dai circuiti a) e b), ottenendo
I3 = I3′ + I3′′ =
6
R2
R1
V1
V2
·
·
R2 R3 +
R3
R2 + R3 R1 + R2 +R3
R1 + R3 R2 + RR11+R
3
(10)
Circuiti equivalenti, teoremi di Thévenin e di Norton
L’analisi dei circuiti elettrici può essere facilitata sostituendo interamente o parzialmente
una rete con un circuito equivalente che, per lo scopo che ci si propone, ha le stesse caratteristiche dell’originale. Tale procedura, peraltro già vista per i circuiti serie e parallelo,
può essere estesa al caso di un intero circuito lineare comunque complesso riducendolo a
due soli elementi finali.
Teorema di Thévenin
Qualsiasi circuito elettrico lineare attivo può essere schematizzato con un circuito
costituito da un generatore ideale di tensione Veq e da una resistenza Req in serie
con esso. Fissati due
punti A e B del circuito
dato, Veq è la d.d.p. esistente tra A e B e
Req è la resistenza che
il circuito presenta tra
A e B nelle condizioni
Figura 5: Teorema di Thévenin
6
in cui tutti i generatori ideali di tensione sono sostituiti con tratti di corto circuito e i
generatori ideali di corrente sono aperti. Ne segue che se tra i punti A e B si inserisce un
nuovo ramo di resistenza R, in esso passa una corrente
I=
Veq
.
R + Req
(11)
Per dimostrare la (11), che è l’espressione algebrica del teorema di Thévenin, si può ricorrere al teorema di sovrapposizione: si supponga infatti di porre in serie alla resistenza
R del ramo aggiunto tra A e B un generatore la cui tensione sia uguale a quella esistente
a vuoto tra A e B. La corrente circolante in tali condizioni, che è nulla, deve uguagliare,
per il teorema di sovrapposizione, la somma di quella, I, circolante per effetto del solo
generatore di d.d.p. Veq e di quella, −I, circolante per effetto del nuovo generatore aggiunto. Da tale uguaglianza segue immediatamente la (11).
La resistenza Req può essere determinata come rapporto tra la d.d.p. Veq (detta anche
tensione a vuoto per rimarcare il fatto che essa è la d.d.p. esistente tra A e B nel circuito
originario, senza l’inserimento di alcun nuovo ramo) e la corrente I0 (detta corrente di
corto circuito) che circola in un ramo di resistenza nulla mediante il quale A viene connesso con B.
Vediamo subito un esempio di applicazione di questo teorema. Dato il circuito mostrato in figura (ponte di Wheatstone) si determini l’intensità della corrente I5 che circola nella
resistenza R5 del ramo aggiunto tra A
e B. Per il teorema di Thévenin I5 =
Veq
. Si tratta di determinare Veq e
R5 +Req
Req . Per trovare Req basta notare che la
sostituzione di un corto circuito al posto del generatore di d.d.p. V porta ad
avere che la resistenza vista tra A e B
non è altro che la serie delle resistenze
parallelo R1 //R3 e R2 //R4 e quindi
Req =
Figura 6: Ponte di Wheatstone
R1 R3
R2 R4
+
.
R1 + R3 R2 + R4
(12)
Per trovare Veq , ovvero la d.d.p. VA −VB
esistente tra A e B nel circuito originario, si osservi che essa è data dalla differenza tra
(VA − VC ) e (VB − VC ). Dette quindi I1 e I2 le correnti in R1 (ed R3 ) e in R2 (ed R4 ) si ha
Veq = I1 R1 − I2 R2 =
V
V
R1 −
R2 .
R1 + R3
R2 + R4
(13)
Teorema di Norton
Qualsiasi circuito elettrico lineare attivo può essere schematizzato con un circuito costituito da un generatore ideale di corrente Ieq e da una resistenza Req in parallelo ad esso.
7
Fissati due punti A e B del circuito dato, Ieq è la corrente di corto circuito tra A e B e
Req è la resistenza già definita nel teorema di Thévenin. Questa seconda forma di circuito
equivalente è utile quando ha interesse considerare generatori di corrente ed è coerente
con la schematizzazione di Thévenin.
7
Trasferimento di potenza da un generatore ad un
carico
Dato il circuito in figura, dove V0 è un generatore di tensione, caratterizzato da una
resistenza interna R0 , ed R rappresenta la resistenza di carico, la massima
potenza che il generatore può erogare
Wmax è quella che corrisponde alla massima corrente, ottenibile chiudendo il
generatore stesso su un corto circuito
(R = 0). In tali condizioni I = V0 /R0 e
quindi Wmax = I 2 · R0 = V02 /R0 .
Se invece R 6= 0, la potenza W dissiV0
Figura 7:
pata dall’intero circuito è W = V0 R+R
0
mentre la potenza Wu effettivamente utilizzata è quella dissipata dal carico R:
Wu =
V0
R + R0
2
R=
V02 R
(R + R0 )2
Wu è quindi funzione della resistenza di carico R ed in particolare presenta un massimo
per R = R0 che è uguale alla metà della potenza dissipata in totale. Infatti
∂Wu
=0
∂R
→
R = R0
→
(Wu )max =
V02
1
1 V02
= WR=R0 =
4R0
2
2 2R0
In tal caso (R = R0 ) la potenza erogata dal generatore, che è la metà di quella massima
Wmax , viene equamente ripartita tra R e R0 .
8
Elementi reali di circuito elettrico
8.1
Resistori
Un resistore è un elemento di circuito dotato di uno specifico valore di resistenza. Questi
valori vanno da pochi ohm (Ω) o frazione di ohm a migliaia di ohm (kΩ) e milioni di ohm
(MΩ). I simboli convenzionali usati per una resistenza sono quelli mostrati in fig.8. I
resistori possono essere costruiti in diversi modi:
• resistori a filo
per un filo conduttore vale la seguente legge (seconda legge di Ohm)
R=ρ
8
l
S
(14)
Figura 8: Simboli dei resistori
dove ρ è una costante caratteristica del materiale di cui è fatto il filo, che prende
il nome di resistenza specifica o resistività, l la lunghezza e S la sezione del filo.
Avvolgendo in spire il filo di lunghezza l e sezione S costante è possibile realizzare
delle resistenze ad alta precisione purché la sostanza usata abbia una ρ abbastanza indipendente dalla temperatura; materiali molto usati sono la manganina, la
costantana e l’argentana.
• resistori a pellicola
Sono ottenuti depositando una sottile pellicola metallica oppure un sottile strato
di granuli di carbone su un supporto cilindrico isolante. La difficoltà di depositare
pellicole di spessore rigorosamente costante ha come conseguenza la scarsa precisione
delle resistenze ottenute, ma questi resistori hanno tuttavia il vantaggio di non
risentire di effetti capacitivi e induttivi come quelli a filo.
• resistori ad impasto
Sono ottenuti comprimendo il carbone in granuli in forma di cilindro insieme con
altre sostanze isolanti, ottenendo in tal modo resistenze molto elevate.
Sulla superficie esterna dei resistori a pellicola e ad impasto vengono di solito tracciate
bande colorate che permettono di conoscere il valore in ohm della resistenza mediante un
codice di colori (vedi fig.9). La banda più vicina all’estremità del resistore rappresenta la
prima cifra significativa, la seconda la seconda cifra significativa e la terza banda il numero degli zeri da aggiungere alle prime due cifre significative secondo il codice di seguito
riportato:
colore
numero
nero
0
marrone rosso
1
2
arancio giallo verde
3
4
5
azzurro
6
viola grigio bianco
7
8
9
Resistenze con valori compresi tra 1 e
10 Ω sono indicate con una terza banda dorata mentre una terza banda color
argento indica resistenze tra 0.1 e 1 Ω.
La quarta banda, che può avere colore
marrone, rosso, oro e argento, indica la
tolleranza sul valore indicato dalle prime
Figura 9: Resistore
9
tre bande. Il colore marrone indica una tolleranza di ±1%; il colore rosso una tolleranza
di ±2%, il colore oro una tolleranza di ±5% e l’argento di ±10%. Se la quarta banda è
assente la tolleranza è del ±20%. Indicando con a, b, c e d i valori numerici corrispondenti a ciascuna delle 4 bande, nel loro ordine, si può quindi determinare il valore della
resistenza e della sua incertezza tramite le seguenti semplici relazioni:
R = (10a + b) · 10c
∆R = (d/100) · R
(15)
Sui resistori di alta potenza (P ≥ 1 W ) al posto del codice di colori viene spesso
utilizzato un codice alfanumerico nel quale una lettera indica la posizione della virgola e
l’unità di misura. Sono utilizzate 3 lettere: R indica che l’unità di misura è Ω, K per kΩ e
M per MΩ. Ad esempio un resistore su cui sia riportato un codice 47R ha una resistenza
di 47 Ω, per un codice 4R7 si ha 4.7 Ω, per un codice R47 si ha 0.47 Ω. In questi casi
anche la tolleranza è indicata tramite una ulteriore lettera successiva al codice resistivo:
la lettera M corrisponde ad una tolleranza del 20%, K al 10%, J al 5%, G al 1% e F al
1%.
Le dimensioni del resistore sono legate alla potenza massima che è capace di dissipare
senza un apprezzabile aumento di temperatura causato dall’effetto Joule. Valori tipici
di questa potenza massima sono 1 W, 1/2 W e 1/4 W, ai quali corrispondono valori
decrescenti delle dimensioni del resistore.
Può essere utile inserire in un circuito elementi con valori di resistenza variabili. Si parla
allora di “potenziometri” con tre terminali e di “reostati”, che hanno due terminali (vedi
fig.8). I potenziometri sono realizzabili con un filo di lega, o con un supporto conduttore
depositato su un materiale isolante, sul quale scorre un pattino, detto cursore, che realizza
un contatto strisciante. La maniera più semplice per realizzare un reostato è quella di
collegare tra loro il cursore e un estremo del filo di lega di un potenziometro.
Nella misura di resistenze e nel loro impiego bisogna tener conto di due possibili fonti di
errore:
• resistenza delle connessioni e dei contatti, che assume importanza relativamente a
resistenze basse, e cattivo isolamento dei terminali, che può dar luogo a fenomeni
perturbativi di dispersione nel caso si vogliano realizzare resistenze elevate;
• capacità non infinita (come ci si aspetterebbe nel caso in cui siano assenti i piccoli effetti capacitivi legati alla presenza di conduttori affacciati) e induttanza non
nulla del resistore (dovuta ad effetti di induzione tra le varie parti conduttrici che
costituiscono il resistrore).
Per i motivi sopra elencati un resistore reale viene spesso schematizzato tramite la serie
di un resistore e di un induttore ideali, con in parallelo un condensatore ideale.
8.2
Condensatori
I condensatori possono avere capacità fissa o variabile. Quelli a capacità fissa più diffusamente usati sono:
10
• condensatori a carta o a mica, costituiti da due sottili fogli metallici separati da un
sottile strato di isolante, o dielettrico, come la carta o la mica. Questo insieme viene
arrotolato in modo da fargli assumere forma cilindrica, ricoperto di isolante e dotato,
per le connessioni, di due fili metallici collegati ciascuno con una delle armature. Per
aumentare la capacità il dielettrico deve essere il più sottile possibile; in tal modo
però si riduce la massima tensione che può essere applicata senza che l’isolante
sia danneggiato dall’intenso campo elettrico prodotto dalle cariche presenti sulle
armature. Inoltre, il piccolo spessore e la grande superficie dell’isolante aumentano
la resistenza di perdita tra le armature.
I condensatori a dielettrico di carta o di mica sono disponibili con capacità variabili
da 0.001 a 1 µF e possono essere usati in circuiti in cui la tensione massima è
dell’ordine delle centinaia di V;
• condensatori a ceramica ed a film di plastica, realizzati depositando le armature in
forma di sottile strato metallico direttamente sul dielettrico. I dielettrici di plastica
hanno resistività molto alta, cioè resistenza di perdita molto piccola. L’elevata
costante dielettrica di molte ceramiche consente di ottenere notevoli capacità con
piccole dimensioni del condensatore.
• condensatori elettrolitici, costituiti da un foglio metallico ossidato immerso in una
pasta o soluzione conduttrice. Il sottile strato di ossido è il dielettrico tra il foglio
metallico e la soluzione, e proprio il suo piccolo spessore consente di raggiungere
elevati valori di capacità (da 1 a 103 µ F). La tensione applicata non può tuttavia
superare qualche V, ed il foglio metallico non deve mai assumere potenziale negativo
rispetto alla soluzione, altrimenti lo strato di ossido viene danneggiato da effetti elettrolitici. Per evitare questo inconveniente, sull’involucro esterno del condensatore
è riportata la segnalazione del terminale al quale deve essere applicata la polarità
negativa.
Il valore della capacità di un condensatore è usualmente riportato in forma estesa oppure
segue un codice alfanumerico o di colori simile a quello visto per i resistori.
I condensatori a capacità variabile sono di
solito costituiti da due insiemi di strati metallici alternati, uno fisso e l’altro rotante intorno
ad un asse in modo da poter variare l’area della superficie affacciata degli strati. Poiché il
dielettrico è l’aria, è necessario lasciare tra le
armature una certa distanza affinché ruotando non si tocchino. Il valore massimo della
capacità ottenibile non supera all’incirca i 500
Figura 10: Condensatore
µF. Il valore minimo della capacità, quando gli strati non sono sovrapposti, si aggira intorno a 10 µF.
I condensatori variabili trimmer usano un dielettrico di mica; vengono di solito regolati
per mezzo di un giravite e sono comunemente usati quando la capacità deve essere variata
solo raramente. I valori di capacità ottenibili sono pressappoco gli stessi che per conden11
satori variabili che hanno come dielettrico l’aria.
I simboli convenzionalmente usati per i condensatori sono rappresentati in fig.10. Il segno
curvo rappresenta il terminale negativo nel caso di condensatori elettrolitici e l’armatura
esterna nei condensatori a carta o a mica; questa convenzione può essere utile per connettere correttamente i condensatori, anche se per i condensatori a carta e a mica la polarità
della tensione applicata è indifferente.
La schematizzazione più utilizzata per un condensatore reale, almeno fino a che non si
opera con segnali varabili nel tempo con frequenza superiore alla decina di MHz, è quella
di un condensatore ideale con in parallelo un resistore ideale, la cui resistenza è legata
agli effetti di perdita del dielettrico interposto tra le due armature del condensatore reale.
8.3
Induttori
Sono costituiti da molte spire di filo conduttore, ciascuna isolata dalle adiacenti, avvolte
su un supporto. Circuiti elettronici ad alta frequenza impiegano spesso induttori le cui
induttanze sono dell’ordine di 10−6 H che possono essere realizzate dall’avvolgimento
di poche spire su un supporto del diametro di circa 1 cm. Qualche decina di spire dà
valori di induttanza intorno a 10−3 H. Induttanze fino a parecchie centinaia di henry, da
usarsi a basse frequenze, sono ottenute avvolgendo molte centinaia di spire su un nucleo
di materiale ferromagnetico, in particolare ferro. Questo nucleo è sovente laminato allo
scopo di interrompere le correnti indotte (correnti di Foucault) da variazioni del flusso
di induzione magnetica; questo accorgimento riduce le perdite per effetto Joule. Per lo
stesso motivo, cioè per diminuire le perdite causate da correnti parassite, per frequenze
elevate vengono usati induttori con nucleo di ferrite, che è un materiale ferromagnetico ad
alta resistività. Gli induttori a ferrite non sono usati a basse frequenze perché le proprietà
magnetiche di questo materiale non sono altrettanto favorevoli quanto quelle del ferro.
Il valore dell’induttanza di un induttore è usualmente riportato in forma estesa oppure segue un codice alfanumerico o di colori simile a quello visto per i
resistori.
I simboli convenzionalmente usati per
gli induttori sono rappresentati in fig.10.
Con a) viene riportato il simbolo per un
induttore, mentre con b) quello per un
induttore con nucleo di ferro o ferrite.
Si possono ottenere induttanze variabili
Figura 11: Induttore
muovendo l’avvolgimento rispetto al nucleo, ma componenti di questo tipo sono raramente usati; la maggior parte degli induttori
sono ad induttanza fissa.
La miglior rappresentazione dal punto di vista elettrico di un induttore reale è quella di
un induttore ideale con in serie un resistore ideale (di resistenza pari a quella del filo che
costituisce l’avvolgimento) e, in parallelo a questi due componenti, un condensatore ideale
(la cui capacità è legata al fatto che si hanno dei conduttori affacciati tra loro).
12
8.4
Generatori reali
Un generatore reale di tensione può essere schematizzato mediante la serie di un generatore
ideale di tensione e di un resistore di resistenza Rint che rappresenta la resistenza interna
del generatore. A differenza di quanto accade nel caso del generatore ideale di tensione, la
d.d.p. VR ai capi A, B del generatore reale quando tra essi è inserito un carico R dipende
dal carico stesso; se IR è la corrente che circola a carico R inserito e V0 la d.d.p tra i capi
del generatore a circuito aperto si ha infatti
R
1
V0
(16)
VR = IR · R = V0 ·
= V0 ·
IR =
Rint + R
Rint + R
1 + RRint
da cui si vede che un generatore reale di tensione approssima un generatore ideale (per il
quale V = V0 = cost.) tanto meglio quanto più la resistenza di carico R è grande rispetto
alla resistenza interna Rint .
Si definisce forza elettromotrice (f.e.m.) di un generatore reale di tensione la d.d.p. presente tra i capi del generatore a circuito aperto (nella simbologia da noi adottata, V0 ). I
generatori reali di tensione sono sistemi mediante i quali si realizza la trasformazione in
energia elettrica di energia di altra natura (meccanica, chimica, termica, ecc.). Un tipico
generatore reale è rappresentato da un “alimentatore di tensione” che opera un raddrizzamento della tensione alternata fornita in un normale impianto elettrico domestico. Il
valore della resitenza interna per tali alimentatori è dell’ordine dell’ohm, ma si trovano in
commercio anche alimentatori, cosiddetti “stabilizzati”, che, grazie ad un circuito di controllo interno, forniscono in uscita una tensione continua di valore indipendente dal carico,
purché la corrente erogata si mantenga entro limiti dichiarati. In tali casi la resistenza
interna è praticamente nulla.
La pila costituisce un altro esempio di generatore reale
in cui energia chimica viene trasformata in energia elettrica; il simbolo convenzionalmente adottato per la pila è
rappresentato in fig.12, in cui il tratto più lungo e sottile
rappresenta il polo positivo e quello più corto e spesso
il polo negativo. Le resistenze interne delle comuni pile
variano da 0.1 ad alcune decine di Ω, a seconda del tipo
Figura 12: Pila
di utilizzo.
Un generatore reale di corrente può essere schematizzato mediante il parallelo di un
generatore ideale di corrente e di una resistenza Rint che è la resistenza interna del generatore.
L’intensità della corrente che un generatore reale di corrente è capace di far circolare in
una resistenza R inserita tra i suoi terminali dipende da R. Dette IRint e IR le correnti in
Rint ed R si ha infatti
I0 = IRint + IR
IRint Rint = IR R
(17)
da cui
IR = I0 ·
Rint
1
= I0 ·
Rint + R
1 + RRint
13
(18)
Come si vede, un generatore reale di corrente approssima un generatore ideale (per il
quale IR = I0 = cost.) tanto meglio quanto più la resistenza interna Rint è grande rispetto
alla resistenza di carico R.
9
9.1
Misure in corrente continua
Misure di intensità di corrente con l’amperometro
Un amperometro è uno strumento tarato con il quale si eseguono misure di intensità di
corrente. Esso è caratterizzato dalla portata, dalla resistenza interna e dalla classe:
- la portata è l’intensità di corrente massima misurabile If.s. , cioè quella per la quale
l’indice si porta al fondo scala (f.s.);
- la resistenza interna è la resistenza elettrica complessivamente presentata dallo strumento;
- la classe è un numero che convenzionalmente indica la sensibilità di lettura consentita
dall’amperometro, ed è pari a 100 volte l’errore relativo ∆I/If.s. sulla corrente di fondo
scala. Se ad esempio un amperometro è di classe 2 , l’errore relativo sulla corrente di
fondo scala è del 2%, e l’errore assoluto su quella scala è pari al 2% della corrente di
fondo scala. E’ possibile misurare con un amperometro correnti di intensità maggiore
di quella di f.s. inserendo in parallelo alla resistenza interna RA opportune resistenze.
Tali resistenze, dette resistenze di shunt, sono di solito predisposte all’interno dello strumento e la loro utilizzazione si ottiene mediante un opportuno inserimento dei puntali
oppure mediante l’utilizzo di comandi situati sul pannello frontale dello strumento stesso.
La fig.13 mostra una resistenza di shunt Rs connessa in
parallelo a RA ; con ovvi simboli si ottiene
I = Is + IA
IA RA = Is Rs
(19)
da cui
IA = I
Rs
RA + Rs
(20)
Figura 13: Misura di corPerciò si ottiene I moltiplicando l’intensità IA della corrente
s
rente misurata dall’amperometro per un fattore costante k = RAR+R
(ad es. se Rs =
s
0.1 · RA si ha k ≃ 10).
Una misura di intensità di corrente con l’amperometro si esegue interrompendo il ramo in cui scorre la corrente da misurare e richiudendolo mediante lo strumento. Nel far questo
si modifica però il circuito originario
perché vi si inserisce la resistenza interna RA , o il parallelo tra RA e Rs , dell’amperometro; al fine di eseguire una
Figura 14:
14
corretta misura di intensità di corrente è necessario valutare l’entità della perturbazione
arrecata onde poter eseguire l’eventuale correzione. In fig.14 è riportata la schematizzazione secondo Thevenin del circuito in studio, prima e dopo l’inserimento dell’amperometro.
La corrente da misurare ha intensità I = V0 /R0 . L’intensità IA letta sull’amperometro è
V
0
I
V0
= R0RA =
IA =
RA + R0
1 + R0
1 + RRA0
(21)
Come si vede l’entità della correzione da apportare al valore letto IA dipende dal rapporto
tra la resistenza interna RA dello strumento e la resistenza equivalente R0 del circuito. La
A
correzione è da ritenersi trascurabile se RRA0 = I−I
è molto minore dell’errore percentuale
IA
commesso nella lettura di IA . Il valore di RA è indicato nel libretto di istruzioni che di
solito correda l’amperometro.
9.2
Misure di differenza di potenziale con il voltmetro
Il voltmetro è uno strumento tarato con il quale si eseguono misure di differenze di potenziale mediante la misura dell’intensità di corrente che fluisce in un resistore di resistenza
nota. In pratica basterebbe utilizzare un misuratore di corrente collegato in serie con un
resistore di resistenza RV nota e avente la scala moltiplicata per il valore di RV .
Per misurare la d.d.p. tra due punti A e B il voltmetro, che è sostanzialmente un
amperometro con un’elevata resistenza interna RV , si dispone tra A e B, in parallelo
al ramo o ai rami di circuito preesistenti tra A e B.
Anche la portata di un voltmetro, definita come la massima
d.d.p., misurabile, cioè quella per la quale l’indice va al fondo
scala, come quella di un amperometro può essere aumentata; in
questo caso però la resistenza di shunt Rs deve essere messa in
serie alla resistenza interna. Infatti (vedi fig.15) se VA − VB è la
d.d.p, da misurare, IV l’intensità della corrente deviata nel ramo
dello strumento, VV e Vs le d.d.p. rispettivamente ai capi di RV
e di Rs , si ha
Figura 15: Misura di
d.d.p.
VA − VB = IV (RV + Rs ) = VV + Vs
(22)
Se Rs = (n − 1)RV avremo che Vs = (n − 1)VV ed infine VV = (1/n)(VA − VB ). Si può
allora ricavare VA − VB moltiplicando per n la d.d.p. VV misurata dal voltmetro.
L’inserimento di un voltmetro in un circuito ne perturba le condizioni di equilibrio
preesistenti perché parte della corrente continua che fluisce viene deviata attraverso la resistenza interna RV del voltmetro. Allo scopo
di valutare l’entità della perturbazione si può
considerare la schema secondo Thévenin del
Figura 16:
voltmetro
Misura di d.d.p.
con
15
circuito in studio prima e dopo l’inserimento del voltmetro (vedi fig.16). La d.d.p. da
0
misurare è V0 ; la corrente che circola in RV ha intensità IV = RVV+R
per cui la d.d.p. ai
0
capi del voltmetro (che è quella che lo strumento misura) è quindi
1
V0
RV = V0
VV = IV RV =
RV + R0
1 + RRV0
→
V0 = Vv
R0
1+
RV
(23)
Come si vede l’entità della correzione da apportare al valore letto Vv dipende dal rapporto
R0
tra la resistenza equivalente R0 del circuito e la resistenza interna RV del voltmetro.
RV
V
La correzione è da ritenersi trascurabile se il rapporto V0V−V
è minore dell’errore perV
centuale commesso nella lettura di VV .
1
Il valore di RV si calcola a partire dall’inverso If.s.
della corrente di fondo scala del mil1
liamperometro base del voltmetro. Il valore di If.s. , espresso in Ω/V e detto impropriamente sensibilità voltmetrica, uguaglia, per la legge di Ohm, il rapporto tra la resistenza
1
interna RV e la d.d.p. di fondo scala Vf.s. . Per ottenere RV basta quindi moltiplicare If.s.
1
per Vf.s. . Se, ad esempio, If.s.
= 20.000 Ω/V , la resistenza interna del voltmetro, quando
lo si usi con il fondo scala 50 V , è RV = 20.000 Ω/V · 50 V = 1MΩ.
9.3
9.3.1
Misure di resistenza
Metodo voltamperometrico
Dopo aver connesso la resistenza incognita ad un opportuno generatore, questo metodo
consiste nel misurare la d.d.p. ai suoi capi e l’intensità della corrente che vi fluisce,
applicando poi la prima legge di Ohm.
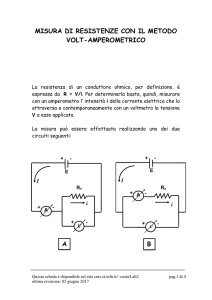
Nel realizzare tali misure si possono presentare i due casi illustrati in fig.17, in
cui amperometro e voltmetro sono disposti diversamente.
Caso a) - Il voltmetro misura una d.d.p.
VV uguale a quella VR ai capi di R, ma
l’amperometro misura una corrente IA
diversa dalla corrente IR che percorre R.
Figura 17: Metodo voltamperometrico
Per trovare come il rapporto tra le letture effettuate sia legato al valore vero della resistenza R si può utilizzare le leggi di
Kirchhoff per ottenere
IA ·
RV R
= IR R
RV + R
IR = IA ·
→
RV
RV + R
(24)
da cui
VV
VR
=
R=
IR
IA
R
1+
RV
16
(25)
Caso b) - L’amperometro misura una corrente IA uguale a quella IR che scorre in R,
ma il voltmetro misura una d.d.p. VV diversa dalla d.d.p. VR ai capi di R. Partendo
nuovamente dalle leggi di Kirchhoff si ricava
RA
RA
VV = IR (R + RA ) = IR R 1 +
= VR 1 +
(26)
R
R
e si ottiene
VV
1
VR
=
R=
(27)
IR
IA 1 + RA
R
Come si vede, nel caso a) il valore di R è tanto meglio approssimato dal rapporto VIAV quanto
più piccolo rispetto a 1 è il rapporto RRV ; nel caso b) quanto più piccolo rispetto a 1 è
il rapporto RRA . In ambedue i casi l’approssimazione introdotta dovrà essere confrontata
con l’incertezza di misura, al fine di valutarne la significatività.
9.3.2
Ponte di Wheatstone
Questo metodo si presta a misure notevolmente precise di resistenze in un vasto intervallo
di valori (≃ 10−2 ÷ 106 Ω). Il circuito usato è rappresentato in fig.18, dove Rx è la
resistenza incognita, R1 , R2 ed R3 sono resistenze note, delle quali almeno una variabile,
R un reostato per regolare l’intensità della corrente totale, P un generatore di tensione, G
un milliamperometro, Rs una resistenza di shunt,
T e T1 due tasti. Chiuso T1 e regolata opportunamente R col tasto T inizialmente chiuso, in modo
che il milliamperometro sia protetto dalla resistenza
di shunt, e successivamente aperto, per realizzare le
condizioni di massima sensibilità, si varia R finché
si realizza la condizione VB = VD per cui il ponte si
dice bilanciato. In tali condizioni nel ramo BD non
passa corrente e ciò viene controllato mediante il
milliamperometro, usato in questo caso come strumento di zero.
Nelle resistenze R1 ed Rx scorre dunque la stessa corrente I1 e nelle resistenze R2 ed R3 la stessa
corrente I3 . Valgono quindi le relazioni
Figura 18: Ponte di Wheatstone
R1 R3
R1 I1 = R2 I3
Rx I1 = R3 I3
→
Rx =
(28)
R2
9.3.3
Ohmetro
L’ohmetro è uno strumento tarato con il quale si eseguono misure di resistenza in modo
semplice e rapido anche se non con elevata sensibilità e precisione. Un ohmetro è costituito essenzialmente da una pila P e da un milliamperometro A ai quali viene connessa la
resistenza Rx da misurare. Evidentemente la corrente che passa nel milliamperometro
è funzione della resistenza Rx e, se la scala del milliamperometro è tarata in ohm,
17
Figura 19:
IA = I
Rs
P
=
RA + Rs
Rint + Rx +
l’indicazione dello strumento permette di leggere direttamente il valore di Rx . In realtà il semplice
schema sopra riportato non permette di variare la
sensibilità dello strumento né di tener conto di eventuali variazioni della f.e.m. del generatore. Occorre
quindi ricorrere ad uno schema del tipo di quello
riportato in fig.19. Indicando con I la corrente che
percorre la resistenza Rx , con IA quella che passa
nel milliamperometro, con Rs la sua resistenza di
shunt, con P la f.e.m. del generatore e con RA ed
Rint le resistenze interne del milliamperometro e del
generatore si ha
RA Rs
RA +Rs
Rs
P
=
RA + Rs
(Rint + Rx ) 1 +
RA
Rs
+ RA
(29)
Considerati costanti gli altri parametri, l’andamento della funzione IA = IA (Rx ) (ovvero
la funzione che permette la trasformazione della scala milliamperometrica in scala ohmmetrica) è di tipo iperbolico ed ha come conseguenza un progressivo peggioramento dell’incertezza relativa di misura di Rx man mano che ci si avvicina agli estremi (corrispondenti
a IA = If ondoscala per Rx = 0 e a IA = 0 per Rx → ∞). Per tale motivo la misura di
Rx con il multimetro ha massima sensibilità se ci si mantiene tra il 20% e l’80% della
scala; per mantenersi in questo ambito ottimale di misura si dovrà operare cambiando
opportunamente la resistenza di shunt Rs .
La forza elettromotrice P , essendo il generatore realizzato di solito mediante una pila, può
subire variazioni; per compensare tali variazioni si usa regolare finemente la resistenza di
shunt Rs del milliamperometro in modo che lo strumento risulti azzerato quando i puntali
sono in contatto tra loro.
18