Calcolo delle Probabilità 2014/15 – Foglio di esercizi 2†
Calcolo combinatorio.
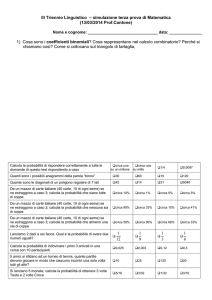
Esercizio 1. In un mazzo di 52 carte da Poker ogni carta è identificata da un seme (cuori
♥, quadri ♦, fiori ♣, picche ♠) e da un tipo (un numero da 1 a 10 oppure J, Q, K). Quindi
il mazzo di carte può essere identificato con l’insieme
M := {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K} × {♥, ♦, ♣, ♠} .
Una “mano” consiste di 5 carte estratte dal mazzo, ossia un elemento dell’insieme
Ω := {A ⊆ M : |A| = 5} .
Munendo Ω della probabilità uniforme, si calcoli la probabilità di ottenere i seguenti punti
(in ordine decrescente di valore):
(a) scala reale (5 carte dello stesso seme e con tipi crescenti in progressione aritmetica di passo 1, per es. {5♥, 6♥, 7♥, 8♥, 9♥}, {8♦, 9♦, 10♦, J♦, Q♦}; le progressioni ammissibili
sono {1, 2, 3, 4, 5}, {2, 3, 4, 5, 6}, . . . , {9, 10, J, Q, K} e infine {10, J, Q, K, 1});
(b) poker (4 carte dello stesso tipo, la quinta arbitraria);
(c) full (3 carte dello stesso tipo, le altre 2 carte dello stesso tipo, ovviamente diverso dal
precedente);
(d) colore (5 carte dello stesso seme, ma non sono in progressione aritmetica di passo 1);
(e) scala semplice (5 carte con tipi crescenti in progressione aritmetica di passo 1, cf. la
scala reale, ma non tutte dello stesso seme);
(f) tris (3 carte dello stesso tipo, le altre 2 arbitrarie, ma tali da non produrre un poker
né un full);
(g) doppia coppia (2 carte dello stesso tipo, 2 altre carte dello stesso tipo diverso dal
precedente, la quinta carta arbitraria, ma tale da non produrre un full);
(h) coppia (2 carte dello stesso tipo, le altre 3 arbitrarie, ma tali da non produrre un tris
né un poker né un full).
Esercizio 2. In una estrazione del Lotto su una determinata ruota vengono estratti a caso
5 numeri tra 1 e 90. Si calcoli la probabilità di fare:
(a) ambata giocando un numero n (cioè n è tra i 5 numeri estratti);
(b) ambo giocando due numeri n, m (cioè n e m sono tra i 5 numeri estratti);
(c) terno giocando tre numeri n, m, k (cioè n, m e k sono tra i 5 numeri estratti);
[Nella realtà che le vincite vengono pagate molto meno di quanto sarebbe “equo”: per
l’ambata si oggiene 11.23 volte la giocata (invece di 18), per l’ambo 250 volte (invece di
400.5), per il terno 4500 volte (invece di 11748).]
Esercizio 3. Si lanciano 12 dadi. Qual è la probabilità che ognuno dei numeri 1, 2, 3, 4, 5, 6
compaia esattamente 2 volte?
†
Ultima modifica: 8 ottobre 2014.
2
Esercizio 4. 21 passeggeri salgono su un treno della metropolitana vuoto formato da 3
vagoni, e ognuno sceglie a caso il vagone su cui viaggiare. Si calcoli la probabilità che
(a) ci siano 4 passeggeri nel primo vagone;
(b) ci siano 7 passeggeri in ciascun vagone;
(c) 5 persone siano su un vagone, 6 su un altro e 10 sul rimanente.
Esercizio 5. Quattro coppie di sposi salgono su un minibus con otto posti a sedere, disposti
in quattro coppie di sedili adiacenti.
Se le otto persone scelgono i posti in modo casuale, qual è la probabilità che ciascuno sposo
sieda accanto alla propria consorte?
Esercizio 6. Una lotteria emette n biglietti, di cui m < n sono vincenti. Qual è la probabilità
che un possessore di r biglietti ne abbia almeno uno di vincente?
Esercizio 7. Si supponga di avere un mazzo di n chiavi diverse. Dovendo aprire una
serratura di cui si ha la chiave, si provano a caso le n chiavi, mettendo da parte quello già
provate, fino a che non si è trovata la chiave giusta. Qual è la probabilità di trovare la chiave
giusta al k-esimo tentativo, con 1 ≤ k ≤ n?
Esercizio 8. Si eseguano n estrazioni casuali con reimmissione da un’urna contenente 2n
oggetti distinti. Sia pn la probabilità che gli n oggetti estratti siano tutti diversi.
(a) Determinare pn .
(b) Introduciamo la notazione an ∼√bn per indicare che an /bn → 1 per n → ∞. Usando la
formula di Stirling n! ∼ nn e−n 2πn, si mostri che pn ∼ c%n , determinando c e %.
Esercizio 9. n paia di guanti vengono mescolate, e poi distribuite a caso a n persone (due
guanti per persona).
(a) Qual è la probabilità pn che ognuno riceva un guanto per la mano destra e uno per la
sinistra?
(b) Si determini√
il comportamento asintotico pn per n → ∞ usando la formula di Stirling
n
−n
n! ∼ n e
2πn.