Sezione Aurea
Aureo
(nombre'dor)
Rapporto
SEZIONE AUREA (Termine GEOMETRICO)
Ripartizione di un segmento in due parti che stanno tra loro (FB':AF) come la maggiore
(AF) sta la segmento intero (AB')
FB' : AF = AF : AB' ma anche per l'invertibilità dei termini della propor zione
RAPPORTO AUREO (Termine MATEMATICO)
AB' : AF = AF : FB' qundi la maggiore (AF) è media propor zionale tra il segmento (AB') e la minore (FB')
Il rapporto aureo è definito quindi come il rapporto tra le parti AF e FB'
Storicamen te è significativo l'uso fatto dai Greci come canone estetico (canone di
Policleto)
poi applicato nel disegno di alcune opere architettoniche (Partenone) e artistiche.
Usata come chiave di lettura delle propor zioni del corpo umano (Fra Pacioli e Leonardo da
Vinci)
riprese in epoca moderna da Le Corbusier come base del suo Modulor.
Sempre più frequenti sono le scoperte legate alla natura basate su tale propor zionalità:
La spirale logaritmica come traiettoria seguita dagli anelli di sviluppo di tante conchiglie
fossili
e gusci di piccoli crostacei.
Ipotesi astrofisica di movimento degli universi secondo traiettorie simili.
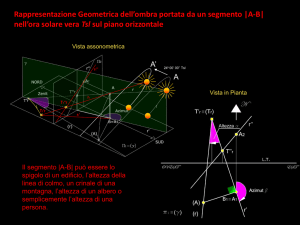
COSTRUZIONE
Dato un segmento AB' si determini sulla perpendicolare in B' un segmento B'C' di
lunghezza pari alla metà del segmento AB'
B'C'=AB' / 2
si disegni la circonferenza di centro C' e raggio B'C' , sulla semiretta C'A si individui il
punto E di intersezione
si riB'alti il segmento AE sul segmento AB' costruendo il segmento AF si otterrà così la
ripartizione del segmento AB'
nelle due parti cercate AF = g e FB'= h tali che AB' : AF = AF : FB'
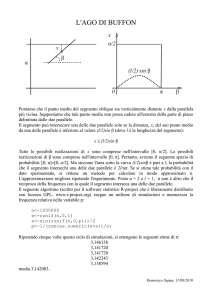
DIMOSTRAZIONE
Per il Teorema di Pitagora
AB'² + AB'² = (AE + AB')²
4
2
sviluppan d o
AB'² + AB'² = AE² + AE·AB' + AB'²
4
4
e semplificando
AB'·(AB' - AE) = AE²
ovvero AB' : AE = AE : (AB' - AE)
e poichè
AE=AF e FB'=(AB' - AE) si ha
AB' : AF = AF : FB' c.v.d.