Corso di Elettrotecnica

Luciano De Menna
Corso di Elettrotecnica
Le motivazioni di tale terminologia si comprendono
facilmente se si considera la seguente situazione. Si
immagini che la tensione del generatore non sia sinusoidale ma semplicemente periodica. Come si è visto,
una tale tensione può essere scomposta in una somma
di infiniti termini sinusoidali di frequenza diversa (le
armoniche della serie di Fourier). Vediamo il circuito
come un doppio bipolo che abbia in ingresso il generatore a frequenza variabile e dal quale si prelevi in uscita la tensione sul resistore R. Evidentemente, per la
sovrapponibilità degli effetti, anche la tensione in uscita può essere vista come somma delle risposte alle singole armoniche. D'altra parte ogni armonica della tensione in ingresso vede una diversa impedenza del circuito a causa della diversa frequenza. Se ne conclude
che le ampiezze delle armoniche con frequenze vicine a
quella di risonanza risulteranno amplificate rispetto
alle altre.
Per questo motivo si dice che il circuito si è comportato come un filtro, lasciando "passare" di preferenza un
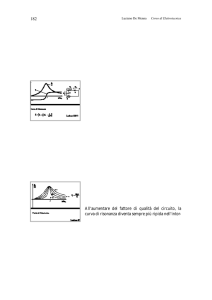
determinato intervallo di frequenze (banda), e attenuando le altre. Così, per esempio, se in ingresso abbiamo una onda quadra, il cui sviluppo in serie di Fourier
abbiamo già visto, in uscita avremo un andamento temporale che sarà tanto più vicino ad una sinusoide quanto più alto è il fattore di qualità (curva di risonanza più
ripida!). Se la frequenza di risonanza del circuito è pari
a quella della fondamentale armonica dell'onda quadra, in uscita si avrà una sinusoide a quella frequenza;
essa sarà leggermente deformata per la presenza delle
armoniche di ordine superiore che, seppur attenuate,
sono sempre presenti. Ma se la frequenza di risonanza
del circuito è uguale a quella della succesiva armonica
(di frequenza tripla di quella fondamentale, nel nostro
183
Luciano De Menna
184
Corso di Elettrotecnica
caso) ecco che in uscita comparirà la terza armonica.
Coerentemente con tutto ciò, se il circuito è sintonizza to sulla seconda armonica - se cioè la sua frequenza di
risonanza è pari al doppio di quella della fondamentale dell'ingresso - in uscita si avrà un segnale nullo. Lo
sviluppo in serie di Fourier dell'onda quadra, infatti,
non prevede armoniche pari!
Le applicazioni che sfruttano il fenomeno della risonanza nelle reti elettriche sono numerosissime e tutte di
importanza eccezionale; a titolo di puro esempio citiamo quello del circuito di sintonia di un apparecchio
radiofonico o televisivo: quando ruotiamo la manopola
della sintonia di un ricevitore possiamo immaginare di
non fare altro che modificare la capacità di un circuito
risonante, variando quindi la sua frequenza di risonanza, in modo tale da selezionare l'opportuna banda che
desideriamo filtrare.
È interessante notare che l'introduzione del concetto di
potenza media ci consente di dare una interpretazione
del fattore di qualità di un circuito risonante in termini
di energie in gioco. Alla risonanza infatti l'energia totale immagazzinata nel condensatore e nell'induttore è
pari a:
2
2
W t = 1 Li t + Cv2 t = 1 L IM sen2 ωt +
2
2
2
2
+ 1 C VM sen2 ωt + π = 1 L IM sen2 ωt +
2
2 2
(VI.32)
2
I
2
+ 1 C M cos2 ωt = 1 L IM sen2 ωt +
2 2
2
2
ωC
0
2
2
+ 1 L IM cos2 ωt = 1 L IM .
2
2
Essa è dunque costante ed uguale all'energia massima
immagazzinata nell'induttore (o nel condensatore).
D'altra parte l'energia dissipata nel resistore in un
Luciano De Menna
Corso di Elettrotecnica
periodo è pari a R I2T per cui si ha:
2
2
Q = ω0 L = ω0 LI T = 2πLI .
R
RI2 T
RI2 T
185
(VI.33)
Se ne deduce dunque:
energia immagazzinata
Q=2π
. (VI.34)
energia dissipata in un periodo
Esercizi
Le potenze richieste, nell'esercizio proposto in precedenza sono:
Pa = 5 W; Qc = 10 VAr; QL = - 5 VAr .
Per l'esercizio successivo ci limitiamo a mostrare alcuni passi della soluzione.
186
Luciano De Menna
Corso di Elettrotecnica
La stessa soluzione può anche essere ottenuta applicando la regola del partitore di corrente.
Ancora un esercizio sulla verifica della conservazione
delle potenze nella prima immagine in colonna.
Nei due esercizi successivi si chiede il calcolo delle
impedenze equivalenti dei bipoli mostrati.
Infine l'ultimo esercizio richiede la soluzione della rete
con il metodo dei fasori.
Luciano De Menna
Corso di Elettrotecnica
Daremo ora un rapido cenno agli strumenti di misura
di tensione e corrente in regime dinamico. Come nel
regime continuo, voltmetri e amperometri vanno inseriti il primo in parallelo al carico ed il secondo in serie
allo stesso. Trattandosi però di grandezze che variano
nel tempo occorrerà stabilire cosa intendiamo in effetti misurare. Per il regime sinusoidale, o più in generale
alternativo, abbiamo diverse scelte: possiamo avere
voltmetri o amperometri che forniscono il valor massimo della tensione o della corrente nella loro evoluzione temporale, o strumenti che forniscano il valor medio
in un periodo od in un semiperiodo della grandezza da
misurare. Per quanto detto in precedenza sulla potenza nei regimi sinusoidali, è chiaro però che il caso più
interessante è quello del voltmetro e dell'amperometro
che forniscono il valore efficace della tensione o della
corrente.
Naturalmente, per gli stessi motivi descritti per gli analoghi strumenti in continua, occorrerà che il voltmetro
abbia una elevata impedenza interna, mentre l'amperometro dovrà presentare una bassa impedenza interna.
Uno strumento molto diffuso nei laboratori o, comunque, nella pratica operativa, è il multimetro. Si tratta di
un dispositivo molto duttile che può essere voltmetro,
amperometro ed altro ancora, semplicemente variando
la posizione di opportuni commutatori.
In regime dinamico, però, può sorgere la necessità di
misurare, istante per istante, l'andamento temporale di
una grandezza elettrica; gli oscilloscopi, o anche oscillografi, siano essi digitali o analogici, svolgono appunto una tale funzione. Il risultato della misura è un gra-
205
206
Luciano De Menna
Corso di Elettrotecnica
fico, evidenziato su di uno schermo o tracciato su di un
foglio, che rappresenta appunto l'andamento nel
tempo della grandezza. Particolare complessità e raffinatezza richiedevano, un tempo, gli oscilloscopi in
grado di rilevare anche grandezze non periodiche.
Oggi un tale problema è brillantemente risolto con
l'uso del calcolatore come strumento di misura o,
comunque, di sistemi di acquisizione dati sotto forma
digitale. In pratica il segnale viene misurato automaticamente, utilizzando un opportuno trasduttore, in un
gran numero di istanti egualmente distanziati nel
tempo; i risultati delle misure vengono memorizzati
come dati e possono successivamente essere visionati
nella modalità desiderata. È chiaro che una volta
memorizzato il risultato della misura sotto forma di
sequenza di numeri, è possibile immaginare ogni sorta
di successiva elaborazione degli stessi mediante calcolatore. Ciò ha fatto oggi del calcolatore - o di dispositivi digitali progettati per scopi specifici - lo strumento
principe di ogni sistema di misura in laboratorio.
Esistono in commercio software molto raffinati ai quali
è possibile demandare, con estrema semplicità, tutta la
gestione di un esperimento o di un processo.
Un strumento di cui non si sentiva particolare necessità
in continua, ma che è di interesse in regime sinusoidale, è il wattmetro: lo strumento che misura la potenza
attiva. In continua infatti, la potenza è data dal prodotto VI, e può essere facilmente ottenuta con due misure,
rispettivamente, di tensione e di corrente. In alternata
invece la potenza attiva è VIcosϕ, e sarebbero quindi
necessarie tre misurazioni, avendo però a disposizione
uno strumento in grado di misurare lo sfasamento tra
tensione e corrente. Fortunatamente esistono strumenti in grado di fornire direttamente il prodotto VIcosϕ
con una sola misura. Nel wattmetro dovremo distin-
Luciano De Menna
Corso di Elettrotecnica
guere due coppie di morsetti: i morsetti voltmetrici,
che verranno collegati ai punti tra i quali insiste la
d.d.p., e quelli amperometrici che dovranno essere
attraversati dalla corrente, così come mostrato nelle
immagini a lato. Si parlerà di circuito amperometrico e
circuito voltmetrico del wattmetro.
Il wattmetro dunque è, per sua natura intrinseca, un
doppio bipolo ed è facile convincersi in base a ragionamenti simili a quelli già sviluppati per il voltmetro e per
l'amperometro, che esso deve presentare, per essere
ideale, una impedenza infinita ai suoi morsetti voltmetrici ed una impedenza nulla a quelli amperometrici.
Esistono anche strumenti che misurano la potenza reattiva assorbita da un carico: essi vengono detti Varmetri
dal nome della unità di misura che abitualmente si utilizza per le potenze reattive, i volt-ampere reattivi.
Esercizi
Per la rete di figura, già proposta, la tensione ai morsetti A e B, ottenuta applicando il teorema del generatore equivalente di corrente, è:
vAB t = 200 sen ωt - π 4 .
Nell'esercizio successivo è presente un accoppiamento
mutuo; non sarà difficile risolverlo se si utilizzerà il circuito equivalente dell'accoppiamento e si ricondurrà
l'impedenza secondaria al primario.
L'ultimo esercizio proposto richiede di rifasare un carico, di cui sono date le caratteristiche, a cosϕ = 1. È un
caso puramente teorico, scelto per semplificare i calcoli, in quanto, per motivi che sarebbe lungo spiegare in
questa sede, non si richiede mai un rifasamento totale.
207