Concetto di pH: soluzioni di acidi e di basi

Elettrochimica
Una cella elettrochimica è costituita da due elettrodi chiamati CATODO e
ANODO.
CATODO → avviene la RIDUZIONE es. Na+ + e- → Na
ANODO → avviene l’ OSSIDAZIONE
es. Cl- → 1/2Cl2 + e-
FORZA ELETTROMOTRICE (f.e.m) = differenza di potenziale tra i
due elettrodi.
Misura la tendenza ad avvenire della reazione redox; misura la facilità con
cui gli elettroni vengono ceduti dal riducente all’ossidante.
Per convenzione alla semireazione di ossidazione dell’H3O+ si assegna
potenziale zero (in condizioni di attività di H3O+ e H2 unitarie):
H2 +2H2O → 2H3O+ + 2e-
(semireazione di ossidazione di riferimento)
Costruendo una cella in cui una delle due semireazioni è quella di
ossidazione di H3O+ a H2 (E° = 0) e l’altra è quella di riduzione di
qualsiasi coppia redox è possibile per differenza calcolare il potenziale di
riduzione della seconda semicella.
f.e.m della cella è sempre > 0
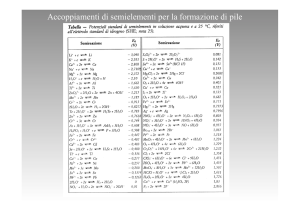
POTENZIALI STANDARD (E°) →
unitarie di tutte le specie coinvolte.
misurati a 298K e con attività
Il potenziale non dipende dal numero di elettroni ceduti o acquistati quindi
rimane uguale anche quando tutti i coefficienti vengono moltiplicati per
uno stesso numero ma cambia segno quando la reazione avviene nel verso
opposto.
Es.
Al3+ + 3e- → Al
2Al3+ + 6e- → 2Al
Al → Al3+ + 3e-
E°= -1.66V
E°= -1.66V
E°= +1.66V
Es.1
Calcolare la f.e.m. di una cella in cui una semicella è costituita da un
elettrodo di Zn immerso in una soluzione 1M di ZnSO4 e la seconda di
un elettrodo di Cu immerso in una soluzione 1M di CuSO4. Dire quale
dei due elettrodi funge da anodo.
(E°(Cu2+/Cu) = 0.34V ; E°(Zn2+/Zn) = -0.76V )
Scriviamo entrambe le semireazioni come riduzioni:
Zn2+ + 2e- → Zn
Cu2+ + 2e- → Cu
E° = -0.76V
E° = 0.34V
Perché la f.e.m. sia positiva devo necessariamente invertire la prima
reazione:
ox
red
Zn → Zn2+ + 2eCu2+ + 2e- → Cu
E° = 0.76V
E° = 0.34V
Zn + Cu2+ → Zn2+ + Cu
f.e.m = 1.1V
L’anodo è l’elettrodo di Zn perchè è quello a cui avviene l’ossidazione.
Se si usano i potenziali di riduzione è sempre:
f.e.m. = Eridcatodo - Eridanodo
Notazione convenzionale per una cella elettrochimica:
Zn|Zn2+(1M)║ Cu2+(1M)|Cu
ANODO
CATODO
Equazione di Nernst
Quando le attività (concentrazioni delle specie in soluzione e pressioni
delle specie gassose) non sono unitarie ([ ] ≠1M; P≠ 1 atm):
aA + bB ↔ cC + dD(g)
E = E°- 0.0591/n · log([C]c·P(D)d/[A]a·[B]b)
Dove n= numero di elettroni scambiati
Es.2
Calcolare la f.e.m. di una cella costituita da una barretta di Zn
immersa in una soluzione contenente Zn2+ in concentrazione 1.8M e
una sbarretta di Cu immersa in una soluzione di Cu2+ 0.2M.
(E°(Cu2+/Cu) = 0.34V ; E°(Zn2+/Zn) = -0.76V )
Applichiamo l’equazione di Nernst alle singole semireazioni di riduzione:
Zn2+ + 2e- → Zn
E° = -0.76V
E = E° - 0.0591/2·log[Zn]/[Zn2+] = -0.76 -0.0591/2·log(1/1.8) = -0.75V
Cu2+ + 2e- → Cu
E° = 0.34V
E = E° - 0.0591/2·log[Cu]/[Cu2+] = 0.34 -0.0591/2·log(1/0.2) = 0.32V
f.e.m. = 0.32 – (-0.76) = 1.07V
oppure:
Zn2+ + 2e- → Zn
Cu2+ + 2e- → Cu
Quindi:
E° = -0.76V
E° = 0.34V
Zn → Zn2+ + 2eCu2+ + 2e- → Cu
E° = 0.76V
E° = 0.34V
Zn + Cu2+ → Zn2+ + Cu
1.1V
E = E° - 0.0591/2·log[Zn2+]/[Cu2+] = 1.1 -0.0591/2·log(1.8/0.2) = 1.07V
Es.3
Calcolare la f.e.m. della cella:
Fe2+(8×10-2M)|Fe3+(5×10-3M)║ MnO4-(1M), H3O+ (1M)|Mn2+(5×10-2M)
(E°(MnO4-/Mn2+) = 1.51V; E°(Fe3+/Fe2+= 0.77V)
Semireazione catodica:
MnO4- + 5e- + 8H3O+ → Mn2+ + 12H2O
E° = 1.51V
Semireazione anodica:
Fe2+ → Fe3+ + e-
E° = -0.77V
MnO4- + 5e- + 8H3O+ → Mn2+ + 12H2O
5Fe2+ → 5Fe3+ + 5e-
E° = 1.51V
E° = -0.77V
MnO4- + 5Fe2+ + 8H3O+ → Mn2+ + 12H2O + 5Fe3+ E° = 0.74
E = 0.74 – 0.0591/5·log(0.05)(0.005)3/(1)(0.08)5(1) = 0.81V
×5
Celle a Concentrazione
L’anodo e il catodo sono costituiti dalla stessa coppia redox ma in
concentrazioni diverse.
Es.1
Calcolare la f.e.m. di una cella costituita dalle due semicelle:
1) Ag|Ag+ (0.05M)
2) Ag|Ag+ (0.8M)
e scrivere la notazione convenzionale per la cella. (E°(Ag+/Ag) = 0.80V)
Ag+ + e- → Ag
0.80V
1) E = 0.80 – 0.0591/1·log(1/0.05) = 0.7231
2) E = 0.80 – 0.0591/1·log(1/0.8) = 0.7943
perché f.e.m. si >0 : 1) deve essere l’anodo e 2) deve essere il catodo
f.e.m. = 0.7943 – 0.7231 = 0.0712V
notazione convenzionale: Ag|Ag+(0.05M)║ Ag+(0.8M)|Ag
Es.2
Una cella a concentrazione è costituita da una semicella in cui un
elettrodo di Pt è immerso in una soluzione di HCl 1M e da una
seconda semicella in cui l’elettrodo di platino è immerso in una
soluzione di CH3COOH 1M. Su entrambi gli elettrodi viene fatto
gorgogliare H2 alla pressione di 1 atm. Calcolare la f.e.m.
(Ka(CH3COOH) = 1.76×10-5)
Ox
H2 +2H2O → 2H3O+ + 2e-
1) HCl 1M → [H3O+] = 1M
E = 0 – 0.0591/2·log[H3O+]2/1 = 0
E° = 0
2) CH3COOH 1M
CH3COOH + H2O ↔ CH3COO- + H3O+
1
-x
x
x
1-x
x
1.76×10-5 = x2/(1-x)
x
x= 4.2×10-3 = [H3O+]
E = 0 – 0.0591/2·log[4.2×10-3]2/1 = 0.140V
Perché la f.e.m. sia positiva:
1) catodo (red)
2) anodo (ox)
E = Eox(anodo) – Eox(catodo) = 0.140-0 = 0.140
Il catodo è sempre quello in cui la concentrazione è maggiore.
Es.3
Una cella a concentrazione è costituita da:
a) una semicella in cui un elettrodo di Ag è immerso in una
soluzione 1M di AgNO3.
b) Una semicella in cui un elettrodo di Ag è immerso in una
soluzione satura di AgCl.
La f.e.m. della cella è 0.29V. Calcolare Kps di AgCl.
Rid
Ag+ + e- → Ag
b) anodo
a) catodo
E° = 0.8
Ag → Ag+ + eAg+ + e- → Ag
E = 0.29 = -0.0591/1·log[Ag+]sat/1
[Ag+]sat = 1.24×10-5M
Kps= (1.24×10-5)2 = 1.54×10-10
Es.4
Una cella a concentrazione è costituita da una semicella con un
elettrodo di Pt immerso in una soluzione 1M di HCl su cui viene
inviato H2 alla pressione di 1 atm ed una semicella con un elettrodo di
Pt immerso in una soluzione 1M di acido formico (HCOOH) su cui
viene inviato H2 alla pressione di 1 atm. Calcolare la costante
dell’acido formico (Ka) sapendo che f.e.m.= 0.111V.
HCl catodo rid
2H3O+ + 2e- → H2 + 2H2O
HCOOH anodo ox
H2 +2H2O → 2H3O+ + 2e-
0.111= -0.0591/2·log[H3O+]2/1
[H3O+]=1.32×10-2M
HCOOH + H2O ↔ HCOO- + H3O+
1
-1.32×10-2
1.32×10-2 1.32×10-2
1- 1.32×10-2
1.32×10-2
Ka = (1.32×10-2)2/(1-1.32×10-2) = 1.77×10-4
1.32×10-2
Relazione tra E° e costante di equilibrio:
aA + bB → cC + dD
E = E° - 0.0591/n·log[C]c[D]d/[A]a[B]b
298K
È uguale alla KC quando siamo all’equilibrio
La reazione non procede
E=0
E° = 0.0591/n·logKc
Es.
Calcolare la Kc a 298K per la reazione:
I2 + H2S + 2H2O → 2I- + S + 2H3O+
(E°(I2/I-) = 0.54V; E°(S/H2S)= 0.14V)
E° = E°(I2/I-)- E°(S/H2S) = 0.54-0.14 = 0.40
Kc = 3.4×1013
0.40 = 0.0591/2·logKc
I2 + 2e- 2I-
2
S= → S + 2e-
2