Sezione aurea - Università di Pavia

LA SEZIONE AUREA
GIUSEPPE FEDERICO ROSSI ([email protected])
1 – Introduzione
La sezione aurea è un concetto che di norma viene associato in via pressoché esclusiva alle cosiddette
arti figurative, quali la pittura, il disegno, la scultura, l’architettura (Figura 1).
Tale fatto, se da un lato mette in evidenza il campo di applicazione comunemente conosciuto dal grande
pubblico, dall’altro rischia di risultare notevolmente riduttivo.
Infatti prendendo in considerazione alcune discipline che, almeno in apparenza, poco o nulla hanno a che
vedere con le tradizionali arti figurative appena richiamate, si scopre con non poca sorpresa che il concetto di
rapporto aureo viene ad avere una ben più ampia portata, tanto da elevarlo a pieno titolo (assieme a e, π e
pochi altri) a numero “magico” ( … e per molti versi misterioso) della Matematica1.
L’obiettivo del presente scritto sarà quello di illustrare, con finalità didattiche, alcune di queste singolari
proprietà del rapporto aureo.
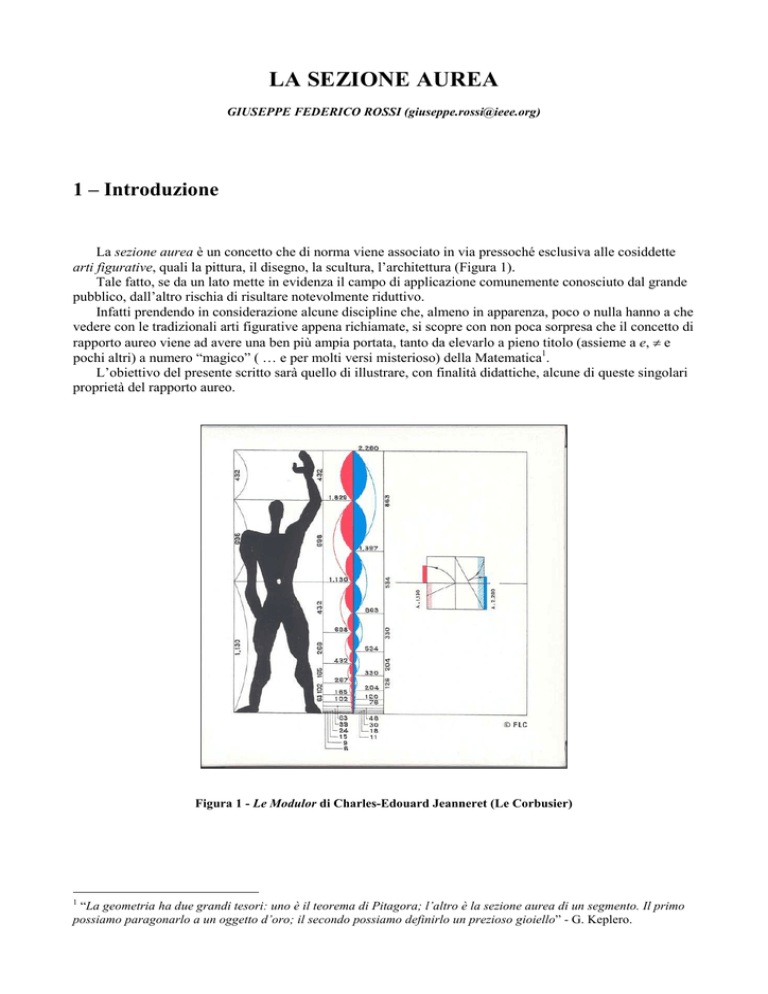
Figura 1 - Le Modulor di Charles-Edouard Jeanneret (Le Corbusier)
1
“La geometria ha due grandi tesori: uno è il teorema di Pitagora; l’altro è la sezione aurea di un segmento. Il primo
possiamo paragonarlo a un oggetto d’oro; il secondo possiamo definirlo un prezioso gioiello” - G. Keplero.
2 – Definizione e calcolo del rapporto aureo
Iniziamo la nostra esposizione fornendo innanzitutto la definizione di rapporto aureo. Visto l’obiettivo
della presente trattazione, al fine di sganciare il concetto generale dalla tradizionale proporzione tra
segmenti, definiremo il rapporto aureo in generale come una proprietà tra numeri reali positivi e non (solo)
tra lunghezze di segmenti non nulli.
Una volta fissata la relazione matematica che definisce il rapporto aureo tra due numeri appartenenti
all’insieme R+-{0}, attraverso lo sviluppo di semplici passaggi algebrici, scopriremo che essa ci condurrà
all’identificazione di un valore numerico ben preciso.
2.1 – La definizione
Definizione 2.1 – Siano dati due numeri a e b che soddisfano alle seguenti proprietà:
a , b ∈ R+-{0}
a<b
Si dice che a e b sono in rapporto aureo quando sussiste la seguente condizione: il numero maggiore (b) è
medio proporzionale tra la somma dei due numeri (a+b) ed il numero minore (a). In formule:
a+b b
=
b
a
(2.1.1)
Il rapporto tra il numero maggiore (b) ed il numero minore (a) prende il nome di rapporto aureo2 e si indica
con la lettera greca Φ, in onore dell’architetto/scultore ateniese Fidia:
Def
Φ=
b a+b
=
a
b
(2.1.2)
Applicando la Def. 2.1 al caso di due segmenti (Figura 2), si perviene alla tradizionale definizione di sezione
aurea fornita dalla Geometria elementare (2.1.3):
A
a
b
B
C
Figura 2
AB + BC BC
=
BC
AB
ove la 2.1.3 esprime il fatto che i segmenti AB e BC sono in rapporto aureo.
2
Oppure, per la 2.1.1, “il rapporto tra la somma dei due numeri ed il maggiore”.
(2.1.3)
2.2 – Calcolo del rapporto aureo Φ
Come enunciato nella Def. 2.1, la relazione fondamentale che definisce il vincolo aureo tra due numeri
reali positivi a e b è l’Eq. 2.1.1. A questa si aggiunge l’Eq. 2.1.2, la quale altro non è che la mera definizione
della quantità chiamata Φ.
In formule si ha:
b a + b
a = b



b
Φ = a

(2.2.1)
Ora, risolvendo il sistema 2.2.1, dimostreremo che Φ risulterà essere un numero indipendente da a e b
(o, detto in modo del tutto equivalente, risolvendo l’equazione che esprime il vincolo aureo, dimostreremo
che b/a risulterà essere un numero).
Consideriamo innanzitutto la prima delle 2.2.1 (vincolo aureo tra a e b):
b a+b
=
a
b
(2.2.2)
b a
= +1
a b
(2.2.3)
Sostituendo ora la seconda delle 2.2.1 (definizione di Φ) nella 2.2.3 otteniamo:
Φ=
1
+1
Φ
(2.2.4)
Prima di proseguire con lo sviluppo della 2.2.4 riteniamo opportuno far notare un dettaglio piuttosto
singolare che, a prima vista, potrebbe essere sfuggito: partendo da un sistema (2.2.1) di due equazioni in tre
variabili (a, b, Φ) siamo pervenuti ad una equazione risolvente (2.2.4) nella una sola incognita Φ.
Questa circostanza, che a prima vista potrebbe apparire piuttosto inusuale, verrà approfondita nel prossimo
paragrafo.
A questo punto risolviamo la 2.2.4 e ricaviamo Φ:
Φ=
1+ Φ
Φ
(2.2.5)
da cui si ottiene la seguente equazione risolvente di 2° grado:
Φ2 − Φ −1 = 0
(2.2.6)
1± 1+ 4
2
(2.2.7)
Φ=
e quindi le due soluzioni sono:
1+ 5
>0
2
1− 5
Φ2 =
<0
2
Φ1 =
(2.2.8)
(2.2.9)
Le soluzioni 2.2.8 e 2.2.9 indicano che la funzione di due variabili Φ = f(a, b) = b/a, quando le sue variabili
indipendenti a e b sono vincolate dalla 2.2.2, assume solo due valori, Φ1 o Φ2 (il fatto che sia Φ=Φ1 oppure
Φ=Φ2 è determinato dai segni di a e b).
Rimandando l’approfondimento di tale singolare circostanza al prossimo paragrafo, completiamo questa
parte con alcune precisazioni in relazione alle due radici Φ1 e Φ2.
Pur essendo Φ2 a tutti gli effetti una soluzione della 2.2.4 (e quindi del sistema 2.2.1) essa deve tuttavia
essere scartata, in virtù delle ipotesi iniziali relativamente ai numeri a e b. Infatti essendo stato fissato
inizialmente per ipotesi (Def. 2.1):
a>0
b>0
a<b
il rapporto Φ=b/a non potrà chiaramente mai essere pari ad un numero negativo (Φ2 = -0,618033988 ……),
né tanto meno avere un valore assoluto strettamente minore di 1 (essendo a < b).
In conclusione l’unica soluzione accettabile è Φ1, secondo la quale il rapporto aureo Φ è un numero
irrazionale positivo indipendente da a e b, pari a:
Φ=
1+ 5
= 1,6180339887498948482045868343656....
2
Q.E.D.
(2.2.10)
2.3 – Perché Φ non dipende da a e b?
Ora approfondiamo la questione lasciata in sospeso nel paragrafo precedente. Il fatto che il sistema 2.2.1
conduca ad un valore di Φ indipendente da a e b non è a prima vista così scontato (…almeno fin tanto che
non si procede a sviluppare algebricamente tale sistema), dal momento che, come evidenziato nel paragrafo
precedente, siamo pur sempre in presenza di un sistema di due equazioni in tre variabili.
Le giustificazioni di tale singolare risultato, chiaramente dovuto alla particolare forma delle equazioni
costituenti il sistema 2.2.1, possono essere molteplici (ripetiamo, oltre alla mera risoluzione algebrica del
2.2.1 riportata nel paragrafo precedente). Vediamone alcune.
Dimostrazione n. 1
Consideriamo l’equazione che definisce il vincolo aureo tra i due numeri reali positivi a e b:
b a+b
=
a
b
(2.3.1)
Moltiplicando ambo i membri per a⋅b si ottiene:
b 2 = a ( a + b)
(2.3.2)
b 2 − ab − a 2 = 0
(2.3.3)
Già a questo punto si intravede una prima giustificazione del fatto che b/a sia pari ad un numero. Infatti la
2.3.3 è una equazione polinomiale omogenea3 nelle variabili a e b. Tale caratteristica fa sì4 che essa, tramite
una divisione per il termine di grado massimo a2, possa essere trasformata in una equazione polinomiale di
secondo grado nell’unica variabile b/a (il rapporto aureo):
2
b b
  −   −1 = 0
a a
(2.3.4)
La 2.3.4, presentando un ∆ > 0, conduce alle due soluzioni Φ1 e Φ2 numeriche calcolate nel paragrafo
precedente, indipendenti da a e b.
Q.E.D.
3
4
Un polinomio si dice omogeneo quando tutti i monomi che lo compongono hanno lo stesso grado.
Sia f(x,y)=0 un’equazione polinomiale omogenea di grado n nelle due variabili x e y:
α0⋅xn + … + αk⋅xn-k yk + … + αn⋅yn = 0
Ora, dividendo ambo i membri per la potenza di grado n (massimo) si ottiene sempre un’equazione:
nella variabile (y/x), se si è diviso per xn
nella variabile (x/y), se si è diviso per yn
Dimostrazione n. 2
Una seconda via per comprendere le motivazioni dell’indipendenza di Φ da a e b si basa sull’analisi del
luogo geometrico rappresentato dall’equazione che esprime il vincolo aureo (2.3.3).
La forma della 2.3.3 indica che la curva in questione è una conica5, anche se, come verrà mostrato tra poco,
di tipo molto particolare.
Risolviamo innanzitutto tale equazione rispetto ad una delle due variabili (ad esempio rispetto a b):
b1 =
a + a 2 + 4a 2 a(1 + 5 )
=
2
2
(2.3.5)
b2 =
a − a 2 + 4a 2 a(1 − 5 )
=
2
2
(2.3.6)
Ora, utilizzando le radici b1 e b2 appena trovate, riscriviamo la 2.3.3 attraverso la ben nota6 formula di
fattorizzazione delle forme polinomiali di secondo grado:

a (1 + 5 )  
a (1 − 5 ) 
b −
 ⋅ b −
=0




2
2

 

(2.3.7)
La 2.3.7, che non è altro che la 2.3.3 semplicemente riscritta, a questo punto ci svela la vera essenza della
conica individuata dal vincolo aureo.
Essa è costituita dall’unione di due rette r ed s (Figura 3) passanti per l’origine, aventi rispettivamente
coefficienti angolari:
mr =
1+ 5
2
(2.3.8)
ms =
1− 5
2
(2.3.9)
La ragione per la quale il luogo di punti r ∪ s, dal punto di vista analitico, risulta essere una conica risiede
semplicemente nel fatto che esso è una conica degenere7.
5
Ricordiamo che si chiamano coniche le curve che si ottengono intersecando una superficie conica con un piano.
Tali curve, in funzione della posizione del piano rispetto alla superficie conica, possono essere di quattro tipi: parabola,
iperbole, ellisse, circonferenza.
Nel piano cartesiano l’equazione generale di una conica è della forma: f(x, y) = αx2 + βy2 + γxy + δx + εy + ζ = 0.
6
7
La formula in questione è: αx2 + βx + γ = α(x-x1)(x-x2) ove x1 e x2 sono le radici di αx2 + βx + γ = 0.
Si chiamano coniche degeneri le curve che si ottengono intersecando una superficie conica con un piano passante per
il vertice del cono. Per contro, si definiscono coniche non degeneri le curve che si ottengono intersecando una
superficie conica con un piano non passante per il vertice del cono (le tradizionali ellisse, iperbole, parabola,
circonferenza).
Più precisamente, essendo la 2.3.3 scomponibile nel prodotto di due polinomi di 1° grado diversi tra loro, il
luogo geometrico r ∪ s è una iperbole degenere8.
A questo punto il motivo per il quale il vincolo aureo (rappresentato dai punti dell’iperbole degenere di
Figura 3) conduce ad un Φ costante pari a Φ1 o a Φ2 (quest’ultimo scartato per le ipotesi iniziali sul segno di
a e b) risulta spiegato.
L’appartenenza del punto (a, b) ad r o ad s fa sì che il rapporto b/a tra le sue coordinate sia rispettivamente
pari a mr o ms e pertanto Φ, che per definizione (2.1.2) è proprio uguale a b/a, in quel caso non può che
essere costante e pari all’uno o all’altro coefficiente angolare (a seconda dell’appartenenza del punto (a, b)
ad r o s).
Q.E.D.
r
s
Luogo dei punti
tali che b/a = Φ 1
Luogo dei punti
tali che b/a = Φ 2
Con il tratteggio sono stati esclusi i valori
non ammessi per le variabili a e b.
Figura 3 – La rappresentazione cartesiana del vincolo aureo (Iperbole degenere)
8
Data una conica degenere, si distinguono i tre seguenti casi:
• Iperbole degenere (coppia di rette passanti per il vertice del cono)
L’angolo formato dal piano con l’asse del cono è strettamente minore dell’angolo di apertura del cono.
Riconoscimento analitico della curva: l’equazione f(x, y)=0 della conica si scompone nel prodotto di due
polinomi di 1° grado diversi tra loro.
• Parabola degenere (retta generatrice passante per il vertice del cono)
L’angolo formato dal piano con l’asse del cono è uguale all’angolo di apertura del cono.
Riconoscimento analitico della curva: l’equazione f(x, y)=0 della conica è il quadrato di un polinomio di 1°
grado (o, detto in modo equivalente, l’equazione f(x, y)=0 della conica si scompone nel prodotto di due
polinomi di 1° grado uguali tra loro).
• Ellisse degenere (un punto, cioè il solo vertice del cono)
L’angolo formato dal piano con l’asse del cono è strettamente maggiore dell’angolo di apertura del cono.
Riconoscimento analitico della curva: l’equazione f(x, y)=0 della conica ammette, in R, solo una soluzione
(un punto).
Dimostrazione n. 3
Per concludere ora illustriamo una terza ed ultima dimostrazione dell’indipendenza di Φ da a e b.
Diversamente dalle considerazioni fatte in precedenza, stavolta le argomentazioni non si baseranno su
strumenti algebrici, bensì su di una semplicissima costruzione geometrica (Figura 4):
P
u’
A’
u
A
B’
B
C’
C
u”
r
A”
B”
C”
t
s
Figura 4
Siano dati due segmenti AB e BC adiacenti (con AB < BC ), le cui lunghezze sono legate dal vincolo aureo.
In tal caso, per definizione, vale la relazione:
AB + BC BC
=
BC
AB
(2.3.10)
Fissiamo un punto P esterno alla retta u passante per A, B e C e da esso tracciamo le rette r, s e t, passanti
rispettivamente per A, B, e C.
Ora tracciamo una (qualunque) retta u’ parallela a u giacente nel semipiano (delimitato da u) al quale
appartiene P: essa interseca r, s, e t rispettivamente nei punti A’, B’ e C’.
Indicato con α il rapporto tra la lunghezza di B’P e la lunghezza di BP, per i criteri di similitudine si ha che il
triangolo ABP è simile a A’B’P, così come BCP è simile a B’C’P. Pertanto:
A' B ' B ' P
=
=α
AB
BP
(2.3.11)
B' C ' B ' P
=
=α
BC
BP
(2.3.12)
A questo punto verifichiamo se anche i segmenti A’B’ e B’C’ sono legati dal rapporto aureo:
A' B ' + B ' C ' ? B ' C '
=
B' C '
A' B '
(2.3.13)
Sostituendo le 2.3.11 e 2.3.12 nella 2.3.13 si ottiene:
α ⋅ AB + α ⋅ BC ? α ⋅ BC
=
α ⋅ BC
α ⋅ AB
(2.3.14)
La 2.3.14 è verificata in quanto, una volta semplificati numeratore e denominatore di ambo i membri per α,
si ottiene la 2.3.10 (che è vera per ipotesi).
Il ragionamento appena esposto può chiaramente essere replicato anche nel caso di una qualunque altra retta
u” parallela a u appartenente al semipiano opposto rispetto a quello cui appartiene P.
In conclusione il rapporto aureo è una relazione tra lunghezze di segmenti, indipendente dalle unità di misura
adottate.
Q.E.D.
3 – Alcune proprietà matematiche del rapporto aureo
Il rapporto aureo presenta un’interessante serie di proprietà matematiche, alcune delle quali vengono
analizzate qui di seguito.
3.1 – Proprietà di base
Vediamo ora un paio di proprietà di base del rapporto Φ, che risultano conseguenza diretta ed immediata
della sua definizione.
Proprietà 1 – Siano dati due numeri reali positivi non nulli a e b (con a < b) in rapporto aureo.
In tale ipotesi il numero minore è medio proporzionale tra la differenza (positiva) dei numeri ed il numero
maggiore. Inoltre il rapporto tra il numero minore e la differenza dei numeri vale Φ.
Dimostrazione
Essendo a e b in rapporto aureo, per ipotesi si ha che (2.1.1 e 2.1.2):
a+b b
=
b
a
(3.1.1)
e
b
=Φ
a
(3.1.2)
Consideriamo la 3.1.1 e sottraiamo 1 membro a membro:
a+b
b
−1 = −1
b
a
(3.1.3)
a+b−b b−a
=
b
a
(3.1.4)
da cui
b−a a
=
a
b
(3.1.5)
Quindi è dimostrata la media proporzionalità del numero minore a.
Capovolgendo numeratore e denominatore della 3.1.5, vista la 3.1.2, si dimostra infine la veridicità
dell’ultima parte della proprietà 1:
a
b
= =Φ
b−a a
(3.1.6)
Q.E.D.
Proprietà 2 – Sia dato il rapporto aureo Φ. Allora i numeri 1/Φ e Φ2 hanno le medesime parti decimali del
numero Φ.
Dimostrazione
Questa proprietà è immediatamente dimostrabile partendo dall’equazione risolvente (2.2.4) utilizzata per
determinare il valore di Φ:
Φ=
1
+1
Φ
(3.1.7)
da cui:
1
= Φ −1
Φ
(3.1.8)
che dimostra che 1/Φ ha la medesima parte decimale di Φ (essendo ottenibile tramite sottrazione di un’unità
da Φ).
Tornando alla 3.1.7 e moltiplicando stavolta ambo i membri per Φ si ottiene:
Φ2 = Φ +1
(3.1.9)
che dimostra che anche Φ2 ha la medesima parte decimale di Φ (essendo ottenibile tramite somma di
un’unità a Φ).
Q.E.D.
3.2 – Espressioni aritmetiche con struttura autosomigliante
Il rapporto aureo presenta un sorprendente legame con alcune espressioni aritmetiche aventi struttura
autosomigliante, ottenute attraverso la composizione di funzioni f con sé stesse per un numero infinito di
volte.
Frazione continua infinita
Vogliamo calcolare il valore α della espressione riportata qui sotto:
1
1+
1+
(3.2.1)
1
1+
1
1+
1
1
1+
1+
1
1+
1
1 + ....
La 3.2.1 è un caso particolare di una ben nota entità matematica chiamata frazione continua9 (in questo caso
frazione continua infinita).
Volendo essere formali, la 3.2.1 può essere equivalentemente espressa anche come segue:
Si consideri la successione fn: N→R così ricorsivamente definita:
1

fn = 
1
1 +

f n −1
se n = 1
se n > 1
con n∈N-{0}
(3.2.2)
La 3.2.1, e quindi il valore α cercato, non è altro che il valore del limite per n→∞ della successione definita
nella 3.2.2:
α = lim f n
n →∞
9
Si definisce frazione continua (semplice) l’espressione della forma:
1
a0 +
1
a1 +
1
a2 +
a3 + ...
con a0 intero e a1, a2, a3, … interi positivi.
(3.2.3)
Ora passiamo a calcolare il valore α. Per fare ciò possiamo seguire vari approcci; ad esempio:
1. La via “tradizionale” potrebbe essere quella di partire dalla definizione della successione 3.2.2 per
poi calcolarne il limite per n→∞.
A tal riguardo va precisato che un simile approccio richiederebbe innanzitutto di determinare
l’espressione α(n), cosa che a prima vista non sembra essere particolarmente agevole.
2. Una via alternativa alla precedente può essere quella che sfrutta la proprietà dell’autosomiglianza
dell’espressione 3.2.1: il valore del denominatore della prima frazione, essendo formato anch’esso da
infinite frazioni annidate, deve essere pari ad α (Eq. 3.2.4).
Viste le complessità dei due approcci appena citati, è evidente che conviene seguire il secondo:
α = 1+
1
1+
(3.2.4)
1
1+
1
1+
1
1
1+
1
1+
1
1+
1 +4....
144442444
3
α
Partendo dalla 3.2.4, è quindi possibile formulare l’equazione che permette di calcolare α:
α = 1+
1
(3.2.5)
α
L'equazione 3.2.5, avendo la stessa forma della 2.2.4, ha quindi le stesse soluzioni:
α1 =
1+ 5
2
(3.2.6)
α2 =
1− 5
2
(3.2.7)
ove la soluzione α2 (negativa) risulta essere non accettabile, e quindi da scartare, in quanto somme e
quozienti di numeri positivi (3.2.1) non possono fornire un risultato negativo.
Pertanto il valore cui tende la frazione continua infinita 3.2.1 è pari al rapporto aureo Φ:
1
1+
1+
=Φ
1
1+
1
1+
1
1
1+
1+
1
1+
1
1 + ....
(3.2.8)
Per completezza vale la pena osservare che si sarebbe chiaramente ottenuto lo stesso risultato se la
considerazione riportata nella 3.2.4 fosse stata applicata in relazione alla seconda ( … o alla terza, o alla
quarta, …) linea di frazione anziché alla prima, in quanto sia sotto la prima linea che sotto la seconda (o la
terza, o la quarta, …) il numero di frazioni è comunque infinito.
Ad esempio, applicando quanto appena detto alla seconda linea di frazione si ottiene:
α = 1+
1
1+
(3.2.9)
1
α
1
α +1
α = 1+
(3.2.10)
α
α = 1+
α
(3.2.11)
α +1
2α + 1
α +1
(3.2.12)
α 2 + α = 2α + 1
(3.2.13)
α=
da cui riotteniamo l’Eq. 3.2.8:
α 2 −α −1 = 0
(3.2.14)
Radice continua infinita
Ora vogliamo calcolare il valore dell’espressione α qui sotto, ottenuta stavolta come radice continua infinita
nella quale si ripete la medesima struttura:
1 + 1 + 1 + 1 + 1 + .....
(3.2.16)
Come nel caso della frazione infinita, anche la radice infinita può essere riformulata in maniera formale
attraverso la seguente successione fn: N→R così ricorsivamente definita:
1

fn = 
 1+ f
n −1

se n = 1
con n∈N-{0}
(3.2.17)
se n > 1
Il valore di α nella 3.2.16 non è altro che il limite di tale successione per n→∞:
α = lim f n
n →∞
(3.2.18)
Procedendo ora in modo del tutto analogo al caso precedente, vista la struttura autosomigliante
dell’espressione 3.2.16, il valore del radicando della radice più esterna deve chiaramente essere pari ad
(1+α):
α = 1 + 1 + 1 + 1 + 1 + .....
1444
424444
3
(3.2.19)
α
A questo punto, alla luce della considerazione appena fatta, dalla 3.2.19 è quindi possibile derivare
l’equazione che consente di determinare α:
α = 1+α
(3.2.20)
da cui elevando al quadrato:
α 2 = 1+α
(3.2.21)
α 2 −α −1 = 0
(3.2.22)
1+ 5
, in quanto il valore
2
di una radice quadrata in R (3.2.16), per definizione, non può mai essere negativo.
e quindi si riottene la solita Eq. 2.2.6 che ha come unica soluzione accettabile α =
Pertanto il valore cui tende la radice continua infinita 3.2.16 è pari al rapporto aureo Φ:
1 + 1 + 1 + 1 + 1 + ..... = Φ
(3.2.23)
3.3 – Reti elettriche: scala infinita di resistori lineari
Nella Teoria delle reti elettriche una struttura circuitale concettualmente interessante (anche se non
realizzabile in pratica) è quella costituita da una scala infinita di resistori lineari tutti uguali, connessi tra loro
secondo lo schema di Figura 5.
Il problema che ci poniamo qui è quello di calcolare la resistenza R tot vista all’ingresso della rete, al fine
di constatare se vi sono delle relazioni con il rapporto aureo Φ.
R
Rtot
R
R
R
R
R
R
.........
Figura 5 - Scala infinita di resistori lineari uguali
Come si può notare il problema è formalmente simile ai due visti nel par. 3.2, in quanto anche in questo
caso il sistema in questione gode della proprietà dell’autosomiglianza.
Infatti immaginando di sezionare la rete nel punto in cui è connessa la prima maglia da sinistra (Figura
6), si ha che la resistenza di ingresso osservata ai morsetti esterni guardando la porzione di destra, proprio
perché anch’essa costituita da infiniti elementi, deve essere ancora pari a R tot:
R
R
R
Rtot
R
R
R
R
.........
Figura 6 - La rete sezionata dopo il primo elemento
Alla luce di quest’ultima considerazione (concettualmente identica a quanto osservato nelle risoluzioni
delle 3.2.4 e 3.2.19) il circuito di Figura 5 può pertanto essere trasformato nel seguente circuito equivalente
(Figura 7):
R
Rtot
R
Rtot
Figura 7 - Circuito equivalente
Applicando le leggi di riduzione delle resistenze serie-parallelo al circuito di Figura 7, si ottiene la
seguente equazione:
Rtot = R +
1
1
1
+
R Rtot
(3.3.1)
ove Rtot è la nostra incognita ed R è un parametro del problema. Sviluppando la 3.3.1:
Rtot = R +
RRtot
Rtot + R
(3.3.2)
2
Rtot
+ RRtot = RRtot + R 2 + RRtot
(3.3.3)
2
Rtot
− RRtot − R 2 = 0
(3.3.4)
Rtot
R ± R 2 + 4R 2
1± 5
=
=R
2
2
(3.3.5)
Sapendo che R tot<0 è una soluzione priva di significato fisico, e quindi va scartata, il risultato cercato è:
Rtot = R
1+ 5
= ΦR
2
(3.3.6)
da cui risulta che la resistenza R tot osservata ai morsetti esterni è direttamente proporzionale alla resistenza R
dei singoli elementi secondo un coefficiente pari al rapporto aureo Φ.
Questo risultato non deve sorprendere, in quanto già l’Eq. 3.3.1 presentava una forma piuttosto famigliare:
Rtot = R +
1
1
1
+
R Rtot
(3.3.7)
Dividendo ambo i membri per R:
1
Rtot
R


1
1
=
R+

1
1
R
+

R Rtot







(3.3.8)
da cui:
Rtot
1
= 1+
R
1
1 

R +
 R Rtot 
(3.3.9)
e quindi:
Rtot
= 1+
R
1
1
1+
Rtot
R
(3.3.10)
La 3.3.10 appena ottenuta non è altro che l’Eq. 3.2.9 stavolta espressa nell’incognita Rtot/R, la quale ha come
soluzione (positiva e quindi accettabile) il rapporto aureo Φ:
Rtot
=Φ
R
(3.3.11)
da cui si ottiene nuovamente la 3.3.6:
Rtot = ΦR
(3.3.12)
3.4 – Figure geometriche: diagonali di un pentagono regolare
Sia dato un pentagono regolare, cioè un poligono regolare10 formato da 5 lati (Figura 8), avente lato di
lunghezza l.
D
E
C
O
F
72°
36°
36°
36°
A
90°
H
72°
B
G
Figura 8 - Il pentagono regolare
In questa sezione il nostro obiettivo sarà quello di dimostrare che in un pentagono regolare valgono le due
seguenti proprietà:
1. Ogni diagonale che connette due vertici divide le altre diagonali (che connettono una diversa coppia
di vertici) in due segmenti legati tra loro dal rapporto aureo.
2. La lunghezza delle diagonali è pari a Φ volte la lunghezza del lato del pentagono.
10
Si definisce regolare un poligono avente tutti i lati tra loro congruenti e tutti gli angoli interni tra loro congruenti.
Dimostrazione
Per definizione di pentagono regolare sappiamo che valgono queste relazioni:
AB = BC = CD = DE = EA = l
(congruenza tra i lati)
(3.4.1)
EAˆ B = ABˆ C = BCˆ D = CDˆ E = DEˆ A
(congruenza tra gli angoli interni)
(3.4.2)
Sapendo che in un qualsivoglia poligono formato da n lati la somma S delle ampiezze degli angoli interni
(espresse in gradi sessagesimali) è data da:
S = 180°(n − 2)
(3.4.3)
l’ampiezza di ciascuno degli angoli interni (tutti tra loro congruenti) del nostro pentagono regolare è data da:
S 180°(5 − 2)
EAˆ B = ABˆ C = BCˆ D = CDˆ E = DEˆ A = =
= 108°
5
5
(3.4.4)
Ora consideriamo il triangolo ADE. Esso è isoscele in E in quanto i segmenti EA ed ED sono congruenti (per
la 3.4.1) e quindi anche gli angoli alla base AD (diagonale del pentagono) risultano tra loro congruenti.
Pertanto la loro ampiezza può essere calcolata per differenza da 180° (che è la somma delle ampiezze degli
angoli in un qualsivoglia triangolo):
EAˆ D = EDˆ A =
180° − DEˆ A 180° − 108°
=
= 36°
2
2
(3.4.5)
Questo ragionamento può essere ripetuto per tutti i triangoli (CAB, DBC, … ) aventi come base una
diagonale e come lati obliqui due lati consecutivi del pentagono. Tali triangoli:
sono isosceli e tutti tra loro congruenti;
l’ampiezza dell’angolo al vertice è pari a 108°
l’ampiezza di ciascun angolo alla base è pari a 36°
Osservando gli angoli aventi vertice in A, si ha che:
DAˆ C = EAˆ B − ( EAˆ D + CAˆ B ) = 108° − (36° + 36°) = 36°
(3.4.6)
Analogamente, osservando gli angoli aventi vertice in D, si ha che:
ADˆ B = CDˆ E − ( EDˆ A + CDˆ B ) = 108° − (36° + 36°) = 36°
(3.4.7)
Quindi il triangolo ABD:
è isoscele poiché i lati obliqui sono tra loro congruenti (sono diagonali del pentagono);
l’ampiezza dell’angolo alla base in A vale 36° + 36° = 72° quindi stessa cosa dicasi per l’angolo in
B.
Consideriamo il triangolo BFA:
AFˆB = 180° − CAˆ B − DBˆ A = 72°
(3.4.8)
quindi tale triangolo è isoscele (con angolo al vertice in A) ed è pure congruente al triangolo isoscele FCD
(hanno tutti gli angoli ed un lato obliquo uguali)
Pertanto i triangoli isosceli ABD (tratteggiato in rosso) e BFA (tratteggiato in verde), avendo tutti gli angoli
tra loro congruenti, sono simili e quindi il lato obliquo di ABD sta al lato obliquo di BFA come la base di
ABD sta alla base di BFA. In formule:
DB AB
=
AB FB
(3.4.9)
ma per le proprietà del triangolo FCD richiamate appena sopra:
AB = DF
(3.4.10)
quindi sostituendo la 3.4.10 nella 3.4.9 si ottiene:
DB DF
=
DF FB
(3.4.11)
o equivalentemente:
DF + FB DF
=
DF
FB
(3.4.12)
che quindi esprime il fatto che in un pentagono regolare ogni diagonale divide le altre diagonali (che
connettono una diversa coppia di vertici) in due segmenti legati tra loro dalla relazione che definisce il
rapporto aureo (nel nostro caso DF è il medio proporzionale).
Ma, in virtù di quanto visto nel cap. 2, sapendo che se vale la 3.4.12 si ha anche che:
DF + FB DF
=
=Φ
DF
FB
(3.4.13)
ed essendo
DF = CD = l
(3.4.14)
si ha:
DF + FB = Φ ⋅ l
(3.4.15)
che esprime il fatto che in un pentagono regolare la lunghezza delle diagonali è Φ volte la lunghezza del lato.
Notare che la stessa proporzione si ha anche tra i lati obliqui e le basi dei triangoli isosceli quali ABD, ecc., i
quali per tale motivo vengono chiamati triangoli aurei.
Q.E.D.
3.5 – La successione di Fibonacci
Un altro interessante legame con il rapporto aureo lo si trova all’interno della cosiddetta successione di
Fibonacci, che prende il nome dal matematico italiano Leonardo da Pisa detto il Fibonacci (∼ 1170 – 1240).
Per approfondire questo tema iniziamo innanzitutto col richiamare la definizione della successione di
Fibonacci.
Definizione – Si chiama successione di Fibonacci la successione Fn: N→N di numeri interi così
ricorsivamente definita11:
1

Fn =  1
F + F
n −1
 n−2
Def
se n = 1
se n = 2
se n ≥ 3
con n∈N-{0}
(3.5.1)
Applicando ripetutamente la definizione ricorsiva 3.5.1 si ottengono gli elementi della successione di
Fibonacci:
1
1
2
3
5
8
13
21
34
55
……
Ora, volendo determinare l’n-esimo numero della successione, come si deve procedere? Le vie possibili
sono fondamentalmente due.
1. Applicare per n volte la definizione ricorsiva 3.5.1, fino al raggiungimento del termine Fn cercato
(via non certo agevole per n grandi).
2. Utilizzare la cosiddetta formula di Binet12 riportata qui di seguito (3.5.2), la quale fornisce
direttamente l’n-esimo termine della successione di Fibonacci, senza la necessità di calcolare gli n-1
termini precedenti:
n
1+ 5  1− 5 

 

 2  − 2 
 

Fn = 
5
n
(3.5.2)
Richiamati i concetti di base sulla successione di Fibonacci, ora il nostro obiettivo sarà ora quello di
dimostrare un’importante proprietà: il rapporto tra due numeri consecutivi della successione, per n→∞,
tende al rapporto aureo Φ. Più precisamente in formule:
Fn+1
=Φ
n →∞ F
n
lim
(3.5.3)
La 3.5.3 costituisce una delle innumerevoli e spesso sorprendenti proprietà matematiche della successione di
Fibonacci. Per dimostrare tale proprietà si possono seguire vari approcci; qui di seguito ne mostreremo due.
11
Talvolta, anche se raramente, il dominio della successione di Fibonacci viene esteso anche al naturale n=0. In tal caso
si pone per definizione F0 = 0.
In questa trattazione ci atterremo alla definizione più comunemente utilizzata (3.5.1), la quale esclude tale caso.
12
In onore del matematico ed astronomo francese Jacques Philippe Marie Binet (1786 – 1856).
1a dimostrazione
La via più tradizionale per dimostrare la 3.5.3 si basa chiaramente sull’applicazione della formula di Binet
riportata in precedenza (3.5.2):
1+ 5 


 2 


n +1
1− 5 

− 

 2 
5
n +1
1+ 5 


 2 


= lim
Fn +1
= lim
n
n
n →∞ F
n →∞
1+ 5  1− 5 
n

 

 2  − 2 

 

5
lim
(1 + 5 )
n +1
2 n +1
= lim
n→∞
1+ 5
2n
(
(1 − 5 )
−
n +1
2 n +1
1− 5
−
2n
) (
n
n→∞
(
)
n +1
n
1+ 5  1− 5 

 

 2  − 2 

 

(
) (
 1 1 + 5 n +1 − 1 − 5
= lim  ⋅
n
n→∞ 2

1+ 5 − 1− 5
)
n
(
1− 5 

− 

 2 
)
)
n +1
n
n +1
n
=



(3.5.4)
Ora, dividendo numeratore e denominatore dell’argomento del limite per (1+√5)n, la 3.5.4 si trasforma in:
(
)
(
)
n

 1 − 5 1 − 5 n 


1− 5  
1
+
5
 
 
 1+ 5 − 1− 5 ⋅



⋅ 
1+ 5  
1


 2
1 + 5  



2
lim  ⋅
− lim 
 = nlim


n
n 
n
n →∞ 2
→∞
1− 5 
 1 − 5   n→∞ 
1− 5 





 

1 − 


1 − 
 1 − 




1+ 5 
1+ 5 

 1+ 5  



(
) (
)
(3.5.5)
Ma sapendo che |(1-√5)/(1+√5)| è un numero costante13 strettamente < 1 e quindi che
n
1− 5 
 =0
lim

n →∞
1
+
5


(3.5.6)
di conseguenza la 3.5.5 diviene:
(1 + 5 ) (1 − 5 ) ⋅ 0
2
−
1− 0
2
1− 0
=
(1 + 5 ) = Φ
2
Q.E.D.
13
Nel senso che è un numero indipendente dal processo di limite. Esso vale 0,3819660… .
(3.5.7)
2a dimostrazione
Una seconda via per dimostrare la 3.5.3 si basa sul calcolo del rapporto tra due consecutivi numeri di
Fibonacci utilizzando direttamente la definizione 3.5.1:
Fn +1
Fn
F
1
 Fn + Fn −1
= 1 + n −1 = 1 +
 F
Fn
Fn
n

Fn −1

=

 F2 1
F = 1 =1
 1
se n > 1
con n∈N-{0}
(3.5.8)
se n = 1
Ora ponendo:
Fn +1
= fn
Fn
(3.5.9)
e sapendo che di conseguenza sarà
Fn
F
= f n−1 ; n −1 = f n − 2 ; …
Fn −1
Fn − 2
(3.5.10)
la 3.5.8 può essere così riscritta:
1

fn = 
1
1 +

f n −1
se n = 1
se n > 1
con n∈N-{0}
(3.5.11)
La 3.5.11 definisce una successione fn: N→R (la successione avente come elementi i rapporti tra due
numeri di Fibonacci consecutivi).
Come si può notare essa è esattamente uguale alla 3.2.2 vista nel caso delle frazioni continue e pertanto, in
virtù del risultato ottenuto nel par. 3.2, si ha:
lim f n = Φ
n →∞
In conclusione per n→∞ il rapporto tra due numeri consecutivi di Fibonacci tende a Φ:
Q.E.D.
F(n+1)/Fn
A completamento di questo paragrafo, riportiamo infine il grafico (Figura 9) che mostra l’andamento del
rapporto tra due numeri di Fibonacci Fn e Fn+1 consecutivi al variare di n.
Come è possibile osservare, i valori del rapporto Fn+1/Fn si collocano molto vicino a Φ (rappresentato
dalla linea rossa) fin dalle “prime battute” cioè fin dalle prime coppie di numeri, fatto che conferma
ulteriormente lo stretto legame esistente tra il numero aureo e la successione di Fibonacci.
n
Figura 9 – Andamento del rapporto tra due numeri di Fibonacci consecutivi
3.6 – L’albero aureo
I casi analizzati in precedenza hanno mostrato che il numero Φ presenta frequentemente stretti legami
con entità aventi come caratteristica di base l’autosomiglianza (basti pensare alle formule analizzate nel par.
3.2 o alla scala infinita di resistori illustrata nel par. 3.3).
In quest’ultimo paragrafo vogliamo dimostrare una sorprendente relazione esistente tra Φ ed una figura
molto comune della geometria frattale: l’albero.
Consideriamo la figura geometrica rappresentata qui sotto (Figura 10), costituita da un segmento
verticale (che chiameremo “tronco”) di lunghezza non nulla pari ad a:
Figura 10
Applichiamo al segmento di Figura 10 una trasformazione T così definita:
Dato un “tronco”, aggiungiamo due nuovi segmenti che chiameremo “rami”, tali che (Figura 11):
ogni ramo misuri f⋅a (ove f∈R e 0<f<1)
i tre segmenti (tronco + i 2 rami) formino tra loro angoli di 120°.
In buona sostanza, utilizzando la terminologia della Botanica, in cima ad un tronco lungo a vengono fatti
spuntare due nuovi rami (più corti del tronco) lunghi f⋅a, tali che i tre formino angoli di 120°.
Ciascuno dei due nuovi segmenti obliqui generati dalla trasformazione T risulta essere omotetico rispetto al
segmento verticale (tronco), con un rapporto di omotetia pari ad f.
120°
120°
120°
I rami generati applicando la
trasformazione T al tronco
iniziale
Figura 11
A questo punto applichiamo nuovamente la trasformazione T, considerando stavolta come “tronco” ciascuno
dei due segmenti obliqui generati alla prima iterazione:
Ogni segmento obliquo di Figura 11 genererà quindi una nuova coppia di segmenti (Figura 12):
aventi lunghezze pari a f volte la lunghezza del segmento che li ha generati
formanti tra loro e con il segmento che li ha generati angoli di 120°
Facciamo notare che i quattro nuovi segmenti, in virtù del rapporto di omotetia e delle ipotesi iniziali su f,
risulteranno avere lunghezza pari a f 2⋅a < f⋅a < a.
120° 120°
120° 120°
120°
120°
Nuovi rami
Figura 12
Ora applichiamo per la terza volta la nostra trasformazione T considerando come “tronchi” gli ultimi quattro
segmenti appena generati. Ciò che otteniamo è riportato in Figura 13.
Utilizzando il solito colore verde per evidenziare i nuovi rami, osserviamo che in quest’ultima iterazione
sono comparsi 8 nuovi segmenti14.
In generale applicando ripetutamente la trasformazione T per n volte si ottiene una struttura ad albero che, al
crescere di n, aggiunge nuovi rami di lunghezza via via decrescente.
14
Chiaramente all’n-esima iterazione il numero di nuovi segmenti è pari a 2n.
Figura 13
Applicando la trasformazione T per n→∞ si ottiene un’immagine frattale tipo quella riportata in Figura 14:
Figura 14
Quesito
Ci poniamo la seguente domanda: esiste un particolare valore del rapporto di omotetia f tale per cui le due
porzioni di destra e di sinistra della Figura 14 si toccano senza sovrapporsi?
Per poter dare una risposta al quesito posto è necessario individuare una condizione, espressa in forma di
equazione, affinché le porzioni di destra e sinistra dell’immagine frattale di Figura 14 si tocchino al centro.
Per fare ciò dobbiamo prima premettere (e dimostrare) due semplici proprietà relative all’albero costruito
attraverso l’applicazione ripetuta della trasformazione T.
Proprietà 1
Dato il segmento iniziale di Figura 10 (tronco), il valore α (Figura 15) dell’angolo di inclinazione (rispetto
all’orizzontale)15 di qualunque segmento dell’albero ottenuto applicando n volte la trasformazione T, è tale
che: α∈{–30° , +30° , +90°} ∀n
α
Figura 15
In altre parole il nostro albero, qualunque sia il numero di iterazioni n che lo ha generato, non presenta mai
segmenti con inclinazione diversa da –30°,+30°,+90° (Figura 16):
+30°
+90°
–30°
Figura 16 - Le possibili inclinazioni dei segmenti costituenti l’albero
Dimostrazione
Visto che la veridicità della Proprietà 1 va dimostrata per qualunque n (numero di iterazioni), è naturale
utilizzare una dimostrazione per induzione.
Dimostrazione della base induttiva (n=1)16:
La dimostrazione del fatto che la Proprietà 1 sia vera per n=1 è immediata: basta osservare l’albero di Figura
11, ottenuto dall’applicazione del 1° passo iterativo.
15
Per esprimere univocamente l’inclinazione dei vari segmenti (non orientati) costituenti l’albero abbiamo scelto di
utilizzare angoli (rispetto all’orizzontale) appartenenti all’intervallo semichiuso ]–90°,+90°].
16
In alternativa ad n=1 come base induttiva avremmo potuto benissimo scegliere n=0. In tal caso saremmo stati nel caso
particolare α∈{+90°}.
Dimostrazione del passo induttivo:
Per ipotesi la Proprietà 1 vale per un dato n* (che vuol dire: l’albero ottenuto applicando n* volte la
trasformazione T è costituito solo da segmenti con inclinazione –30°, +30°, +90°).
Ora dimostriamo che, sotto tale ipotesi, la Proprietà 1 vale anche per l’albero ottenuto applicando una
ulteriore trasformazione T, cioè per (n*+1). Per fare ciò è sufficiente dimostrare che:
segmenti inclinati di –30°, a seguito dell’applicazione di una trasformazione T, non possono
generare nuovi segmenti con inclinazione diversa da –30°, +30°, +90°;
segmenti inclinati di +30°, a seguito dell’applicazione di una trasformazione T, non possono
generare nuovi segmenti con inclinazione diversa da –30°, +30°, +90°;
segmenti inclinati di +90°, a seguito dell’applicazione di una trasformazione T, non possono
generare nuovi segmenti con inclinazione diversa da –30°, +30°, +90°;
La dimostrazione del passo induttivo, esposta direttamente in forma grafica nella Figura 17, è immediata
conseguenza del fatto che ogni segmento genera sempre una coppia di rami formanti angoli di 120°.
Tutti i possibili risultati dell’iterazione (n*+1), nei casi in cui i segmenti generatori sono inclinati di –30°,
+30° e +90°, sono riportati in Figura 17 (come al solito i nuovi segmenti generati da T sono evidenziati in
verde).
In tale figura viene altresì mostrato che le inclinazioni dei rami generati sono indipendenti dall’estremo di
applicazione del segmento generatore scelto per il loro innesto, poiché scegliere l’uno o l’altro estremo
comporta solo una rotazione di 180° della coppia generata.
Q.E.D.
–30°
30°
90°
30°
90°
–30°
30°
Rami generati
Tronco generatore
90°
30°
90°
30°
–30°
90°
Figura 17
–30°
–30°
Proprietà 2
Ogni segmento inclinato di +30° genera sempre, attraverso una applicazione della trasformazione T, un
segmento inclinato di –30° e viceversa.
Dimostrazione
Per la dimostrazione basta osservare i risultati riportati in Figura 17.
Q.E.D.
Giunti a questo punto affrontiamo il quesito posto inizialmente. Riprendiamo la Figura 13 ed effettuiamo un
paio di ulteriori trasformazioni che ci saranno utili per evidenziare la condizione cercata (Figura 18).
A tal riguardo precisiamo che, per vincoli/comodità di disegno, in Figura 18 non sono stati riportati tutti i
segmenti originati dalle ultime due iterazioni, ma solo quelli che interessano i due sottoalberi evidenziati in
blu, essendo quella la porzione di figura coinvolta nella soluzione del quesito.
Si toccheranno??
Per esigenze d i spazio non vengono riportati i rami
generati dalle u ltime 2 iterazioni a part ire da questi
punti
Figura 18
Consideriamo l’estremo a quota maggiore del segmento verticale sinistro generato alla 2a iterazione, indicato
con P nella Figura 19:
t
–30°
+30°
P
–30°
somma delle proiezioni
dei segmenti verdi
proiezione del
segmento rosso
Figura 19
In virtù della Proprietà 1 appena dimostrata possiamo affermare che:
L’intero sottoalbero con radice in P, che si sviluppa con rami di lunghezze via via decrescenti, è
costituito solo da segmenti inclinati di –30°, +30°, +90°.
Visto che il nostro obiettivo è quello di individuare la sequenza di rami che massimizza lo spostamento
orizzontale da P verso destra, le sequenze che, tra tutte quelle possibili, rendono massimo tale spostamento
sono tutte e sole quelle costituite esclusivamente da segmenti inclinati di –30° o +30° (che forniscono il
medesimo spostamento orizzontale non nullo verso destra) e che quindi non presentano alcun segmento
inclinato di +90° (che, al contrario, fornirebbe uno spostamento orizzontale nullo).
Ci poniamo allora la domanda: esiste nel nostro albero, a partire dal punto P, almeno una sequenza di rami
costituita esclusivamente da segmenti inclinati di –30° o +30°?
La risposta è sì. Infatti una volta che si parte da P e si considera il segmento di destra inclinato di +30° (per
intenderci, quello generato alla 3a iterazione ed evidenziato in Figura 19 con la freccia blu), in virtù della
Proprietà 2, esiste sicuramente un successivo segmento inclinato di –30°, il quale (sempre per la Proprietà 2)
sarà seguito da un segmento inclinato di +30° e così via.
Quindi, a partire da P, esiste una sequenza di successivi segmenti inclinati alternativamente solo di –30° e
+30° che si sposta verso destra, che quindi massimizza lo spostamento verso quella direzione.
Riassumendo, la condizione che deve essere verificata affinché le porzioni di destra e sinistra si tocchino è la
seguente (Figura 19):
La somma delle lunghezze delle proiezioni sull’orizzontale di tutti i rami inclinati +30°, –30°, +30°,
–30°, +30°, –30°, … , generati a partire dal punto P dalla 3a iterazione in poi (evidenziati in verde)
deve coincidere con la lunghezza della proiezione sull’orizzontale del ramo, inclinato di –30°,
generato alla 1a iterazione (evidenziato in rosso).
Precisiamo che la condizione appena enunciata è sufficiente per affermare che le porzioni di destra e di
sinistra del nostro albero si toccheranno in un punto, in quanto non sono ammessi disallineamenti di quota.
Infatti, qualunque sia l’iterazione n, il ramo più sporgente della parte sinistra sarà sempre alla stessa altezza
del ramo più sporgente della parte destra, in quanto le parti destra e sinistra della figura sono simmetriche
secondo l’asse t (Figura 19) qualunque sia il numero n di iterazioni effettuate.
Traducendo in formule la condizione espressa sopra, si ottiene:
f 3 ⋅ a ⋅ cos(30°) + f 4 ⋅ a ⋅ cos(−30°) + f 5 ⋅ a ⋅ cos(30°) + ... = f ⋅ a ⋅ cos(−30°)
(3.6.1)
Dividendo ambo i membri per i fattori comuni (tutti diversi da zero), sapendo che cos(30°) = cos(–30°) e
scrivendo il primo membro in forma compatta, l’Eq. 3.6.1 diviene:
∞
∑f
i
=1
(3.6.2)
i=2
Il primo membro della 3.6.2 altro non è che una somma di infiniti termini di una progressione geometrica di
ragione f avente f 2 come primo termine. Pertanto, nota la formula17 delle progressioni geometriche, l’Eq.
3.6.2 diviene:
f2
=1
1− f
(3.6.3)
da cui:
f 2 = 1− f
(3.6.4)
f 2 + f −1 = 0
(3.6.5)
17
Ricordiamo che la somma dei primi n termini di una progressione geometrica [a1, a2, … , an] con ragione q≠1 è data
dalla formula:
1− q n
S n = a1
1− q
Pertanto, quando 0 < q < 1, la somma di infiniti termini di una progressione geometrica è data da:
a
1 − qn
S ∞ = lim S n = lim a1
= 1
n →∞
n→∞
1− q 1− q
Risolvendo:
f =
−1± 1+ 4 −1± 5
=
2
2
(3.6.6)
Scartando la soluzione negativa in quanto non ha significato nel problema dato, se ne conclude che, affinché
le porzioni di destra e di sinistra della Figura 14 si tocchino, il valore del rapporto di omotetia f deve essere
pari al reciproco del numero aureo Φ:
f =
(
)(
)
−1+ 5
−1+ 5 ⋅ 1+ 5
1
1
=
=
= = 0,61803398874989484820......
2
2 ⋅ 1+ 5
1+ 5 Φ
2
(
)
(3.6.7)
In tal caso la figura frattale che si ottiene prende il nome di albero aureo (in Figura 20 viene riportato un
esempio di albero aureo).
Figura 20 - Esempio di albero aureo
Naturalmente va osservato che nell’albero aureo non solo si toccano le parti destra e sinistra dell’intera
figura, ma anche le parti destra e sinistra di ogni sottoalbero avente come tronco uno qualunque dei segmenti
costituenti l’albero dato.
4 – Ringraziamenti
Un ringraziamento particolare all’Ing. Giovanni Cherubin, dottorando di ricerca presso la Royal
Holloway University of London nonché al caro amico Prof. Ledo Stefanini dell’Università di Pavia, per i
preziosi consigli e l’infinita pazienza nell’opera di revisione delle bozze del presente documento.
5 – Bibliografia
•
•
•
•
Mario Livio, La sezione aurea, Milano, Rizzoli 2003.
Rocco Panzarino, Dio Sezione Aurea Bellezza, Collana di Filosofia Sapientia 10, Fasano, Schena
editore 2005.
Cornelis Jacobus Snijders, La sezione aurea: arte, natura, matematica, architettura e musica, 2ª ed.
Padova, Muzzio 1985.
Aldo Scimone, La Sezione Aurea. Storia culturale di un leitmotiv della Matematica, Palermo, Sigma
Edizioni, 1997.