sintesi

Circonferenza e Cerchio – sintesi – gen.2012
CIRCONFERENZA E CERCHIO
Pag. 1
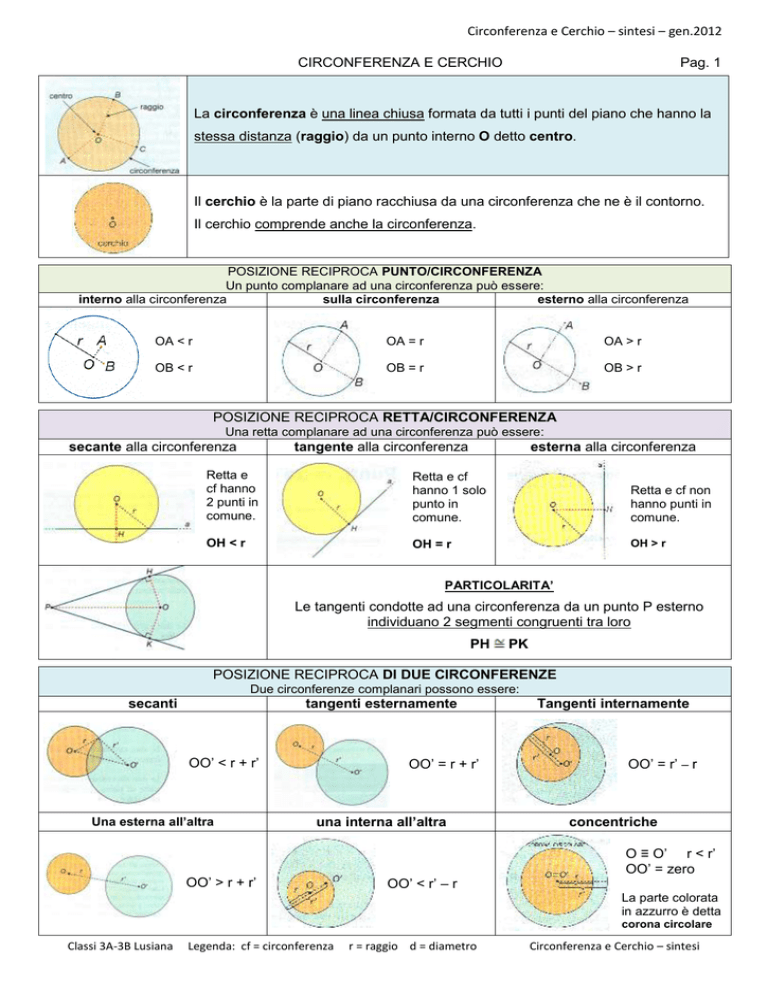
La circonferenza è una linea chiusa formata da tutti i punti del piano che hanno la
stessa distanza (raggio) da un punto interno O detto centro.
Il cerchio è la parte di piano racchiusa da una circonferenza che ne è il contorno.
Il cerchio comprende anche la circonferenza.
POSIZIONE RECIPROCA PUNTO/CIRCONFERENZA
Un punto complanare ad una circonferenza può essere:
interno alla circonferenza
sulla circonferenza
esterno alla circonferenza
OA < r
OA = r
OA > r
OB < r
OB = r
OB > r
POSIZIONE RECIPROCA RETTA/CIRCONFERENZA
Una retta complanare ad una circonferenza può essere:
secante alla circonferenza
tangente alla circonferenza
esterna alla circonferenza
Retta e
cf hanno
2 punti in
comune.
Retta e cf
hanno 1 solo
punto in
comune.
Retta e cf non
hanno punti in
comune.
OH < r
OH = r
OH > r
PARTICOLARITA’
Le tangenti condotte ad una circonferenza da un punto P esterno
individuano 2 segmenti congruenti tra loro
PH
PK
POSIZIONE RECIPROCA DI DUE CIRCONFERENZE
Due circonferenze complanari possono essere:
secanti
tangenti esternamente
OO’ < r + r’
Una esterna all’altra
OO’ = r + r’
una interna all’altra
OO’ > r + r’
Tangenti internamente
OO’ = r’ – r
concentriche
O ≡ O’ r < r’
OO’ = zero
OO’ < r’ – r
La parte colorata
in azzurro è detta
corona circolare
Classi 3A-3B Lusiana
Legenda: cf = circonferenza
r = raggio d = diametro
Circonferenza e Cerchio – sintesi
Pag. 2
Parti di una circonferenza
Arco: parte di circonferenza limitata da 2 punti A e B detti estremi dell’arco.
Corda: segmento che unisce 2 punti della circonferenza.
Diametro: ogni corda passante per il centro.
Ogni diametro divide la circonferenza in 2 semicirconferenze.
Ogni diametro divide il cerchio in 2 semicerchi.
La perpendicolare OH condotta dal centro ad una qualsiasi corda (ad es. AB),
divide tale corda in 2 parti congruenti; essa è quindi asse della corda.
AH
HB
Corde di una stessa circonferenza (ad es. AB e CD) tra loro congruenti
hanno uguale distanza dal centro.
OH
Settore circolare
OK
PARTI DI UN CERCHIO
Segmento circolare ad 1 base
Segmento circolare a 2 basi
ANGOLI AL CENTRO - ANGOLI ALLA CIRCONFERENZA
Si chiama angolo al centro di una
circonferenza ogni angolo avente il
vertice coincidente con il centro della
circonferenza.
Angoli al centro che insistono
su archi congruenti sono tra
loro congruenti.
Si chiama angolo alla circonferenza
un angolo che ha il vertice sulla
circonferenza e I cui lati possono
essere entrambi secanti oppure uno
secante e l’altro tangente alla cf.
In una qualsiasi circonferenza ogni
angolo alla circonferenza è la ½
dell’angolo al centro che insiste
sullo stesso arco.
Circonferenza e Cerchio – sintesi – gen.2012
Tutti gli angoli alla circonferenza
che insistono sullo stesso arco
sono tra loro congruenti.
Angoli alla circonferenza che
insistono su archi congruenti
sono tra loro congruenti.
In una circonferenza ogni angolo alla circonferenza che insiste su una semicirconferenza è un
angolo retto.
Tutti i triangoli aventi un vertice appartenente a una circonferenza e un lato coincidente con un diametro
della circonferenza stessa sono triangoli rettangoli.
TEOREMA DI PITAGORA E CIRCONFERENZA
Il triangolo inscritto in una circonferenza, con un lato coincidente con il diametro,
è un triangolo rettangolo.
In base al Teorema di Pitagora si avrà:
d=
C=
c=
Il triangolo, colorato in azzurro, è rettangolo avente l’ipotenusa uguale al raggio
r, un cateto c uguale alla distanza della corda dal centro O e l’altro cateto
uguale a ½ corda.
In base al Teorema di Pitagora si avrà:
r=
c=
=
Il triangolo, colorato in azzurro, è rettangolo perchè ha i due cateti r e TP
perpendicolari tra loro, in quanto TP è tangente alla circonferenza: OP ne
rappresenta l’ipotenusa i.
In base al Teorema di Pitagora si avrà:
=
Classi 3A-3B Lusiana
Legenda: cf = circonferenza
r =
r = raggio d = diametro
TP =
Circonferenza e Cerchio – sintesi