esami ed esercizi

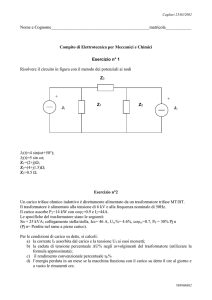
Esercizio 1
Un motore asincrono ha le seguenti caratteristiche: tensione nominale 400 V, frequenza nominale
50 Hz, 4 poli, resistenza equivalente di rotore 0,04 Ω (nella rete equivalente con il rotore riportato a
statore), reattanza equivalente di rotore 0,2 Ω. Determinare la coppia meccanica prodotta dal
motore, alimentato a tensione nominale, quando gira alla velocità di 1450 giri al minuto (assumere
nella formula della coppia Es come la tensione stellata nominale).
Svolgimento proposto:
La rete equivalente semplificata del generatore asincrono con la parte rotorica riportata a statore è:
RS
IS
E
.
I S0
.
I S0
E S
X Rτ 2
RR τ 2
XS
.
I
I SR = R
τ
ZS 0
1 − s 
RR τ 2 

 s 
Per prima cosa si determina lo scorrimento:
la velocità di sincronismo è data da:
ns =
s=
60 ⋅ f 60 ⋅ 50
=
= 1500 rpm
p
2
ns − nm 1500 − 1450
=
= 0.03
ns
1500
l’espressione analitica della caratteristica meccanica è:
C=
3 pRR
E R2
3 pR R
ES2
3 pτ 2 R R
ES2
=
=
ω RR2
τ 2ω RR2
ω ( τ 2R ) 2
2
R
+ s X R2
+ sX R
+ s(τ 2 XR )
s
s
s
perciò, la coppia è:
2
 400 
3 ⋅ 2 ⋅ 0.04 ⋅ 

3 

C=
= 747 Nm
 ( 0.04) 2
2 
2π ⋅ 50 ⋅ 
+ 0.03 ⋅ ( 0.2) 
0
.
03


Esercizio 2
Per il motore precedente, disegnare la caratteristica meccanica per valori di scorrimento 0<s<1.
Svolgimento proposto:
abbiamo già visto che l’espressione analitica della caratteristica meccanica è:
3 pRR
E R2
3 pR R
ES2
3 pτ 2 R R
ES2
C=
= 2
=
ω RR2
τ ω RR2
ω ( τ 2R ) 2
2
2
R
+ s XR
+ sX R
+ s(τ 2 XR )
s
s
s
cerchiamo ora di ricostruire la curva per punti. Il valore della coppia per lo scorrimento pari a 0.03 è
già stato determinato nell’esercizio precedente.
La coppia è massima per un valore dello scorrimento vicino al rapporto:
s=
RR
= 0 .2
XR
per tale valore dello scorrimento si ottiene una coppia pari a 2548 Nm
Calcolando ora vari punti per valori di scorrimento 0<s<1, si ottiene:
3000
2500
C (Nm)
2000
1500
1000
500
0
0
100
200
300
400
500
s/1000
600
700
800
900
1000
Esercizio 3
Per il motore asincrono precedente, determinare la corrente assorbita alla velocità di 1410 rpm per
una tensione di alimentazione uguale al valore nominale (assumere la corrente pari a quella che
scorre nel circuito del rotore riportato a statore).
Svolgimento proposto:
La corrente rotorica della macchina è:
IR =
ER
2
 RR 

 + X R2
 s 
=
ES
2
R 
τ  R  + X R2
 s 
mentre lo scorrimento sarà dato da:
s=
ns − nm 1500 − 1410
=
= 0.06
ns
1500
Rifacendosi alla rete equivalente dell’esercizio 1, si ha:
I SR =
IR
τ
=
ES
2
 τ RR 

 + τ 2 X R
s


2
(
)
=
2
400
3
2
 0.02 
2

 + ( 0 .2 )
 0.06 
= 476 A
Esercizio 4
Per il motore asincrono precedente, determinare il rendimento elettrico sapendo che le perdite nel
circuito magnetico sono pari a 5 kW. Disegnare inoltre per punti la curva del rendimento in
funzione dello scorrimento
Svolgimento proposto:
il rendimento elettrico è dato da:
ηe =
Pu
Pu
=
Pe Pu + Pmagn + Pavv
dove Pu è la potenza all’asse, mentre Pmagn e le Pavv comprendono rispettivamente tutti i tipi di
perdite nel circuito magnetico e nei conduttori (ad esempio le perdite nelle spazzole, quelle negli
avvolgimenti ausiliari, ecc.).
Rifacendoci sempre alla rete equivalente dell’esercizio 1, si può scrivere:
1 − s  2
 1 − 0.03 
2
3 ⋅ τ 2 RR ⋅ 
3 ⋅ 0.04 ⋅ 
 I SR
 ⋅ (127)
 s 
 0.03 
ηe =
=
= 0.859
1 − s  2
 1 − 0.03 
2
2
2
2
2
3 ⋅ τ RR ⋅ 
 I SR + Pmagn + 3 ⋅ τ RR I SR 3 ⋅ 0.04 ⋅ 
(127 ) + Pmagn + 3 ⋅ 0.04 ⋅ ( 127)
 s 
 0.03 
Andando ora a disegnare la curva η e ( s ) per punti, ricordando che:
I SR =
ES
2
τ 2 R R 

 + τ 2 X R
s


si ottiene:
(
)
2
0.9
0.8
0.7
rendimento
0.6
0.5
0.4
0.3
0.2
0.1
0
0
100
200
300
400
500
s/1000
600
700
800
900
1000
Esercizio 1
Per una dinamo con eccitazione in derivazione con tensione di rete 48 V, resistenza di indotto e di
spazzole 2,5 Ω, resistenza di eccitazione 120 Ω, determinare la tensione generata quando la corrente
erogata alla rete è pari a 3 A
Svolgimento proposto:
La rete equivalente semplificata della dinamo con eccitazione in derivazione è la seguente:
Ie
Is
Rs
Ri
Re
E0
l’equilibrio elettrico della rete può essere scritto come segue:
Is =
V − E0
R i + Rs
con
Ie =
V
48
=
= 0 .4 A
Re 120
dall’equilibrio al nodo si ha:
I s = I + I e = 3 + 0.4 = 3.4 A
quindi:
E 0 = V + ( Ri + Rs ) ⋅ I s = 48 + (2.5 ⋅ 3.4) = 56.5 V
I
V
Esercizio 2
Per la dinamo precedente determinare la coppia che deve essere applicata per ottenere il
funzionamento da generatore descritto prima, con una velocità di rotazione pari a 900 giri al minuto.
Svolgimento proposto:
Rifacendoci alla rete equivalente dell’esercizio precedente, l’equilibrio meccanico è espresso dalla:
Cω = E 0 I s
e quindi:
C=
E0 I s
56.5 ⋅ 3.4
=
= 2.04
n
900
Nm
2π ⋅
2π ⋅
60
60
Esercizio 3
Considerando la caratteristica meccanica della coppia di un motore in corrente continua con
eccitazione in derivazione e sapendo che esso assorbe una corrente di 12 A e produce una coppia di
40 Nm, che corrente necessita per avere una coppia di 36 Nm?
Svolgimento proposto:
la coppia per un motore a corrente continua con eccitazione in derivazione può essere espressa
tramite la:
C=
E0 I
30kφ M
=
I
n
π
2π ⋅
60
ed essendo φ M è praticamente costante, si ha:
C
= cos t
I
che graficamente diventa:
C
motore
generatore
I
perciò:
C1 C 2
=
I1
I2
dalla quale:
I2 =
C2 ⋅ I 1 36 ⋅ 12
=
= 10.8 A
C1
40
Esercizio 4
Un motore in corrente continua con eccitazione in derivazione ha le seguenti caratteristiche:
Potenza nominale 7,5 kW, tensione nominale 230 V, rendimento a pieno carico 0,88, la somma
della resistenza di indotto e resistenza di spazzole pari a 0,28 Ω. Calcolare, a pieno carico, la
potenza assorbita, la corrente assorbita, la corrente d’indotto e la forza elettromotrice sapendo che in
questa condizione la corrente di eccitazione è pari a 1 A.
Svolgimento proposto:
La potenza assorbita sarà:
Pass =
Pn 7500
=
= 8.5 kW
η
0.88
la corrente assorbita è data da:
I ass =
Pass 8500
=
= 37 A
Vn
230
lo schema equivalente del motore è:
Ie
Ii
Rs
Ri
Re
E0
dall’equilibrio al nodo posso ricavare la corrente d’indotto:
I i = I ass − I e = 37 − 1 = 36 A
dall’equilibrio elettrico della rete si ricava:
E 0 = V − ( Ri + Rs ) ⋅ I s = 230 − (0.28 ⋅ 36) = 220 V
Iass
V
Esercizio 1
Un generatore sincrono trifase ha le seguenti caratteristiche: potenza nominale 16000 kVA,
frequenza nominale 50 Hz, 2 poli, tensione nominale 3250 V, corrente di eccitazione al sincronismo
per avere una tensione a vuoto pari a quella nominale 18 A, corrente nello statore durante la prova
in corto circuito al sincronismo (quando la corrente di eccitazione è 18 A) 4000 A. Determinare la
rete equivalente della macchina.
Svolgimento proposto:
La rete equivalente semplificata del generatore sincrono trifase è la seguente:
Xs
.
E0
+
_
.
I
+
_
.
E
Dal funzionamento in corto circuito, si ha:
E 0 = Z s Icc
essendo inoltre RS << X S si ottiene:
Xs =
E 0 3250
=
= 0.8125 Ω
I cc 4000
dove la tensione di fase a vuoto E0 e la corrente di corto circuito Icc sono ottenute con lo stesso
valore della corrente di eccitazione.
Esercizio 2
Per il generatore precedente, determinare l’espressione matematica e disegnare la caratteristica
esterna al sincronismo per un fattore di potenza (cosφ) pari a 0,8 (carico ohmico-induttivo).
Svolgimento proposto:
Il comportamento di un alternatore chiuso su di un carico è descritto dalla:
E 02 = E 2 + X s2 I 2 + 2 E X s I senϕ s
che con i valori dati e ricavati nell’esercizio 1 diventa:
3250 2 = E 2 + 0,8125 2 ⋅ I 2 + 2 ⋅ E ⋅ 0,8125 ⋅ I ⋅ 0,6
Inserendo nell’espressione precedente dei valori di I (con 0 ≤ I ≤ I cc ) si ottiene la caratteristica
esterna E(I):
E
0
10
100
500
1000
1500
2000
2500
3000
3500
3900
3990
4000
[V]
3250
3245
3200
2990
2697
2369
2004
1596
1137
614
132
13
0
3500
3000
2500
2000
E (V)
I
[A]
1500
1000
500
0
0
500
1000
1500
2000
I (A)
2500
3000
3500
4000
Esercizio 3
Una macchina sincrona, di cui è riportata la caratteristica a vuoto, è collegata come alternatore ad
una rete prevalente.
Noti i valori della Reattanza Sincrona Xs = 0.375Ω, della Tensione di Rete E = 220 V, e della
Potenza Erogata P = 400 W, e ipotizzando le condizioni di funzionamento lineare, si tracci, in
maniera approssimata (calcolando almeno 3 punti di cui uno sia il minimo) il diagramma della
Curva a V relativa alle condizioni suddette.
Eo
[V]
217.96
218.42
218.88
219.35
220
220.64
221.11
221.57
222.03
Iecc
[A]
78.36
78.73
79.1
79.48
80
80.64
81.11
81.57
82.03
Svolgimento proposto:
Rifacendosi alla rete equivalente dell’esercizio 1, la potenza attiva erogata dalla macchina è:
P=3EIcosϕ
Il comportamento di un alternatore chiuso su un carico è dato da:
E 02 = E 2 + X s2 I 2 + 2 E X s I senϕ
Dalla prima equazione e dalla trigonometria si ottiene:
P2
Isenϕ = ± I −
9E 2
2
ovvero:
E0 =
E + X I ± 2EX S
2
2
S
2
2
P
I −
9E 2
2
Conoscendo l’andamento di E0 con Iecc, posso costruire le curve a V date da I(Iecc). Invece di
esplicitare la I, posso dare io arbitrariamente dei valori alla I e, tramite interpolazione lineare,
P
ricostruire la curva, sapendo che il valore minimo della curva è I =
.
3E
Quello che troverò sarà un grafico del tipo:
I
P = 400W
P
3E
Ie
Esercizio 1
Determinare la rete equivalente di un trasformatore trifase con le seguenti caratteristiche: potenza
nominale 800 kVA, frequenza nominale 50 Hz, rapporto di trasformazione a vuoto
20000
, potenza
400
assorbita nella prova a vuoto eseguita a tensione nominale 3200 W, corrente del primario nella prova a
vuoto 0,17 A, tensione di alimentazione del primario nella prova in corto circuito Vcc% = 4,5%,
potenza assorbita in corto circuito 7500 W. Calcolare inoltre il rendimento convenzionale del
trasformatore.
Svolgimento proposto:
La rete equivalente semplificata della macchina monofase, con il secondario riportato a primario, è la
seguente:
Z cc
Z0
V1n
τ V2
Per determinare la rete equivalente si devono calcolare le due impedenze equivalenti Z 0 e Z cc .
Dalla prova a vuoto, tenendo conto che il trasformatore in esame è trifase, si ricava:
cosψ 10 =
P0
3 ⋅ V1 n ⋅ I 10
V1 n
Z0 =
3 ⋅ I 10
=
=
3200
= 0.54
3 ⋅ 20000 ⋅ 0.17
20000
= 67.92 kΩ
3 ⋅ 0.17
da cui:
R0 = Z 0 cosψ 10 = 36.68 kΩ
X 0 = Z 0 senψ 10 = 57.17 kΩ
Dalla prova in corto circuito si ha:
Vcc =
4.5
⋅ 20000 = 900 V
100
I cc = I 1n =
P1 n
3 ⋅ V1 n
800000
= 23.1 A
3 ⋅ 20000
=
per cui
cosψ cc =
Pcc
3 ⋅ Vcc ⋅ I cc
Vcc
Z cc =
3 ⋅ I cc
=
=
7500
= 0.21
3 ⋅ 900 ⋅ 23.1
900
= 22.49 Ω
3 ⋅ 23.1
da cui
Rcc = Z cc cosψ cc = 4.72 Ω
X cc = Z cc senψ cc = 22.39 Ω
il rendimento convenzionale sarà
ηc =
Pn
800000
=
= 0.987
Pn + P0 + Pcc 800000 + 3200 + 7500
Esercizio 2
Dato il trasformatore dell’esercizio 1, calcolare le perdite negli avvolgimenti (tramite la Rcc) quando la
corrente nel primario è pari all’80% della corrente nominale
Svolgimento proposto:
Dal valore I1n dell’esercizio 1 si ricava la nuova corrente al primario:
I = 0.80 ⋅ I1n = 0.85 ⋅ 23.1 = 18.48 A
Considerando il valore Rcc dell’esercizio 1, la potenza persa negli avvolgimenti, essendo il
trasformatore trifase, non è altro che
Pavv = 3 ⋅ Rcc ⋅ I 2 = 3 ⋅ 4.72 ⋅ (18.48) 2 = 4.84 kW
Esercizio 3
Calcolare la caduta di tensione da vuoto a carico del trasformatore dell’esercizio 1, considerando un
fattore di potenza del carico pari a 0,8 e una corrente assorbita dal carico I12 (secondario riportato al
primario) pari all’80% della corrente nominale
Svolgimento proposto:
Riportando tutto al primario, la rete equivalente del trasformatore è:
Z 1cc
I10
V1
I12
Z0
Dall’esercizio 1, si ha:
V1 = 20000 V
V2 = 400 V
R1cc = 4.72 Ω
X 1cc = 22.39 Ω
I n = 23.1 A
mentre
I 12 = 0.8 ⋅ I n = 0.8 ⋅ 23.1 = 18.48 A
La caduta di tensione da vuoto a carico viene calcolata con:
∆V % =
( R1 cc ⋅ cosψ c + X 1cc sen ψ c ) ⋅ I 12
⋅ 100
V10
ed essendo dai dati cosψ c = 0.8 si ha:
∆V % =
(3.72 + 13.43) ⋅ 18.48
⋅ 100 = 1.6%
20000
τ V2
Per verificare il risultato, riportiamo tutto il sistema al secondario:
Z 2cc
I20
V1
τ
I2
Z0
τ2
V2
In questo caso si ha:
Z 2 cc =
Z1 cc
τ2
e quindi
R2cc =
R1cc 4.72
=
= 1.89 mΩ
τ2
50 2
X 2 cc =
X 1cc 22.39
=
= 8.96 mΩ
τ2
50 2
mentre
I 2 = τ ⋅ I 12 = 50 ⋅ 18.48 = 924
La caduta di tensione è così:
( R2 cc ⋅ cosψ c + X 2cc senψ c ) ⋅ I 2
(1.51 ⋅10 −3 + 5.38 ⋅ 10 −3 ) ⋅ 924
∆V % =
⋅ 100 =
⋅ 100 = 1.6%
V20
400
Esercizio 4
Calcolare la e disegnare la curva di rendimento del trasformatore dell’esercizio 1, considerando un
fattore di potenza del carico pari a 1 e una corrente assorbita dal carico I12 (secondario riportato al
primario) pari al 120%,100%, 80%, 60%, 40% e 20% della corrente nominale
Svolgimento proposto:
Riportando tutto al primario, la rete equivalente del trasformatore è:
Z 1cc
I12
I10
V1
η=
Z0
Pu
Pu + Pavv + Pmagn
dove:
Pu = 3 ⋅ V1n ⋅ I 12 ⋅ cos ϕ
Pavv ≅ 3 ⋅ Rcc ⋅ I 122
Pmagn ≅ P0
Dall’esercizio 1 si ha che Rcc = 4,74 Ω, mentre P0 = 3200 W.
Ponendo cosφ = 1 e I12 = 120% I1n = 27.72 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 27.72 = 960221 W
Pavv ≅ 3 ⋅ 4.74 ⋅ (27.72) 2 = 10880 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9855
Ponendo cosφ = 1 e I12 = I1n = 23.1 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 23.1 = 800 kW
Pavv ≅ 3 ⋅ 4.74 ⋅ (21.3) 2 = 7587 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9867
Zc
Ponendo cosφ = 1 e I12 = 80% I1n = 18.48 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 18.48 = 639408 W
Pavv ≅ 3 ⋅ 4.74 ⋅ (18.48) 2 = 4836 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9876
Ponendo cosφ = 1 e I12 = 60% I1n = 13.86 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 13.86 = 479556 W
Pavv ≅ 3 ⋅ 4.74 ⋅ (13.86) 2 = 2720 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9878
Ponendo cosφ = 1 e I12 = 40% I1n = 9.24 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 9.24 = 320074 W
Pavv ≅ 3 ⋅ 4.74 ⋅ (9.24) 2 = 1209 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9864
Ponendo cosφ = 1 e I12 = 20% I1n = 4.62 A, si ha:
Pu = 3 ⋅ 20000 ⋅ 4.62 = 160037 W
Pavv ≅ 3 ⋅ 4.74 ⋅ (4.62) 2 = 456 W
Pmagn ≅ 3200 W
η=
Pu
Pu + Pavv + Pmagn
= 0.9777
La curva disegnata diviene così:
η
rendimento
0.99
0.988
0.986
0.984
0.982
0.98
0.978
0.976
0.974
0.972
20
40
60
80
I 12 /I 1n %
100
120
Elettrotecnica II
Terni, 28 gennaio 2013
Allievo………………………
Rispondere in modo sintetico alle seguenti domande teoriche
1. Funzionamento a carico di un trasformatore trifase, disegnare inoltre la
rete equivalente in tale caso
2. Trasformatori di misura
3.Caratteristica a vuoto di una macchina sincrona
4. Diagrammi polari e curve a V macchina sincrona
5. Disegnare i grafici degli andamenti della coppia meccanica di una
macchina asincrona in funzione dello scorrimento, della resistenza
addizionale e della velocità di rotazione
6. Schema della rete di un motore asincrono a doppia gabbia, e
diagramma della caratteristica meccanica del motore in funzione delle
gabbie
7. Eccitazione delle macchine a corrente continua
8. Curve caratteristiche della macchina a corrente continua: tensione in
funzione della corrente, velocità di rotazione in funzione della corrente,
coppia in funzione della velocità, velocità di rotazione in funzione della
coppia
9. Diodi a giunzione
10. Schema di convertitore AC/DC trifase a ponte di Graetz
11. Schema di inverter trifase
Elettrotecnica II
Terni, 28 gennaio 2013
Allievo………………………
Rispondere in modo sintetico alle seguenti domande teoriche
1. Schema delle reti equivalenti del trasformatore funzionante a vuoto, a
carico e in cortocircuito
2. Schema e rete equivalente di trasformatori in parallelo, e requisiti per
messa in parallelo
3. Funzionamento in corto circuito macchina sincrona
4. Comportamento dell’alternatore libero macchina sincrona, completo
di disegno del grafico tensione-corrente
5. Funzionamento a vuoto macchina asincrona
6. Reti equivalenti delle macchine asincrone trifasi
7. Caratteristiche esterne della macchina con eccitazione separata e con
eccitazione in derivazione
8. Funzionamento a carico macchina a corrente continua
9. Schema e andamento di tensione e corrente di un raddrizzatore
controllato monofase a semplice semionda
10. Schema di inverter monofase
11. Regolazione dei carichi in AC: tecnica ad impulsi ad ampiezza
modulata (PWM)