Caratteristiche fisiche dell`occhio umano

Caratteristiche fisiche dell’occhio umano
Con gli strumenti dell’Ottica geometrica è possibile analizzare le proprietà fisiche ed il
funzionamento dell’occhio umano. Esso, infatti, è schematizzabile come sistema ottico
approssimativamente centrato: una sequenza di vari elementi diottrici, organizzati in modo da
ricevere raggi da oggetti esterni e formarne immagini reali su di un sensore ad alta risoluzione
spaziale (retina), i cui segnali sono inviati al cervello attraverso il nervo ottico.
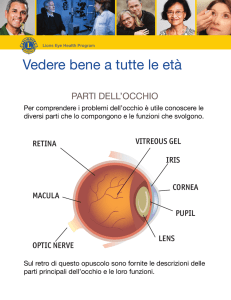
La struttura ottica dell’occhio è visibile nella
figura a lato. Principalmente, si distinguono:
∼
∼
∼
∼
∼
cornea: sottile membrana trasparente,
funzionante come una lente avente
raggi di curvatura praticamente uguali
tra loro, nella quale si realizza la
rifrazione dei raggi luminosi
dall’ambiente esterno all’umore
acqueo; in pratica, un diottro sferico di raggio 𝑅1 ≅ 8𝑚𝑚;
umore acqueo: sostanza che riempie la camera anteriore, spessa 𝑠1 ≅ 3𝑚𝑚, avente indice
di rifrazione 𝑛𝑈𝐴 ≅ 1.33 come quello dell’acqua, di cui è composto al 98%;
cristallino: mezzo trasparente ed elastico indispensabile affinché l’immagine si formi sulla
retina, con indice di rifrazione 𝑛𝐶 non uniforme (variabile al suo interno da 1.40 a 1.45),
assimilabile ad una lente biconvessa, quasi simmetrica ed avente raggio di curvatura 𝑅2
variabile insieme alla sua focale per azione di un sistema di muscoli, detti ciliari;
iride: diaframma circolare, posto tra cornea e cristallino, al cui centro c’è un’apertura
variabile (pupilla) utile a limitare opportunamente il fascio luminoso entrante; esso può
accomodarsi su raggi tra 1𝑚𝑚 e 4𝑚𝑚 a seconda delle condizioni di illuminazione;
umore vitreo: sostanza che riempie buona parte del bulbo oculare, spesso 𝑠2 ≅ 19𝑚𝑚,
avente indice di rifrazione 𝑛𝑈𝑉 ≅ 1.34 vicino a quello dell’acqua e dell’umore acqueo.
Il processo per cui varia la focale del cristallino (unica, nell’approssimazione di lente simmetrica), al
fine di dare immagini reali e capovolte poste esattamente sulla retina, viene usualmente detto di
accomodamento; quello per cui la pupilla sia più o meno dilatata è invece detto di adattamento.
Per un occhio normale (emmetrope) è possibile accomodare immagini di oggetti situati tra il punto
remoto (posto idealmente all’infinito) ed il punto prossimo, a distanza di circa 15𝑐𝑚 dall’occhio.
Tuttavia, il punto prossimo varia da individuo a individuo ed in base all’età. Esiste, inoltre, una
distanza che massimizza l’acuità visiva, ossia la capacità dell’occhio di distinguere i dettagli di un
oggetto: essa è pertanto detta distanza della visione distinta e dista circa 25𝑐𝑚 dall’occhio.
Frequenti disfunzioni dell’occhio sono la miopia, per la quale l’immagine di un oggetto lontano si
forma prima della retina a causa di una eccessiva convergenza del cristallino; e l’ipermetropia, per
cui l’immagine si forma aldilà della retina a causa di un difetto di convergenza del cristallino. Il
primo difetto visivo si corregge con lenti divergenti, mentre il secondo con lenti convergenti.
Un altro possibile difetto è l’astigmatismo, dovuto al fatto che la cornea non è esattamente sferica
Caratteristiche fisiche dell’occhio umano
1
e quindi risulta più convergente nel piano orizzontale che in quello verticale o viceversa; tale
problema si corregge per mezzo di lenti cilindriche.
Sempre nell’approssimazione che vuole le proprietà del cristallino essere ben approssimate da
quelle di una lente sottile simmetrica, è possibile stimare dei limiti nella gamma di variabilità del
raggio di curvatura del cristallino di un occhio normale, ovvero quando questo sia accomodato al
punto remoto o al punto prossimo. Infatti, per la trasmissione attraverso la cornea vale
l’equazione del diottro sferico, che si scrive
𝑛1 𝑛𝑈𝐴 𝑛𝑈𝐴 − 𝑛1
+
=
,
𝑝1
𝑞1
𝑅1
essendo 𝑛1 ≅ 1.00 l’indice di rifrazione dell’aria, 𝑝1 la distanza dell’oggetto dal vertice della
cornea e 𝑞1 la distanza dell’immagine dallo stesso vertice. L’effetto convergente del cristallino,
invece, si quantifica mediante l’equazione
𝑛𝑈𝐴 𝑛𝑈𝑉 𝑛𝐶 − 𝑛𝑈𝐴 𝑛𝑈𝑉 − 𝑛𝐶 2𝑛𝐶 − 𝑛𝑈𝐴 − 𝑛𝑈𝑉
+
=
−
=
,
𝑝2
𝑞2
𝑅2
𝑅2
𝑅2
laddove si intende essere 𝑝2 = 𝑠1 − 𝑞1 la distanza dell’oggetto (immagine prodotta dal diottro –
cornea) dal vertice del cristallino e 𝑞2 = 𝑠2 la distanza della sua immagine dallo stesso vertice, pari
allo spessore del bulbo oculare per la condizione che l’immagine debba formarsi sulla retina.
Allora, in caso di occhio accomodante un oggetto posto nel punto remoto, si ricava
(1)
𝑝1 ~
+ ∞,
(1)
𝑞1
(1)
𝑝2
≅ 32𝑚𝑚,
≅ −29𝑚𝑚 ⇒
(1)
𝑅2
≅ 8.5𝑚𝑚;
mentre, in caso di occhio accomodante un oggetto posto nel punto prossimo, si ottiene
(2)
𝑝1 ≅ 150𝑚𝑚,
(2)
𝑞1 ≅ 38𝑚𝑚,
(2)
(2)
𝑝2 ≅ −35𝑚𝑚 ⇒ 𝑅2 ≅ 6.5𝑚𝑚.
La variazione relativa del raggio del cristallino è circa del 30%. Risulta pure evidente che le
immagini date dalla cornea si formerebbero (in assenza dell’azione convergente del cristallino)
oltre la retina, essendo persino
(1)
𝑞1 > 𝑠1 + 𝑠2 ≅ 22𝑚𝑚
Immaginando, ora, di avere un oggetto 𝐴𝐵 esteso di lunghezza 𝑦, osservato da un occhio normale
in condizioni di luminosità adeguate, ad una distanza pressappoco coincidente con quella della
visione distinta 𝛿 ≅ 25𝑐𝑚, esso si presenta sotto un angolo 𝛼 tale che
𝑦 = tg(𝛼 )𝛿
Ricordato che la maggiore acuità visiva si ottiene posizionando
l’oggetto alla distanza 𝛿, per aiutare l’occhio a distinguere
maggiormente dei dettagli si è soliti ricorrere ad una lente sottile
convergente: la lente di ingrandimento. Infatti, ponendo l’oggetto
tra il primo fuoco della lente e la lente stessa, mentre l’occhio è
Caratteristiche fisiche dell’occhio umano
2
situato in prossimità del secondo fuoco, una lente di ingrandimento migliora la capacità di
percezione di dettagli; essa, in altre parole, fa aumentare l’angolo sotto cui è visto l’oggetto 𝐴𝐵.
L’occhio percepisce l’immagine dell’oggetto sotto un angolo 𝛽 > 𝛼 tale che
𝑦 = tg(𝛽 )𝑓,
essendo 𝑓 la distanza focale della lente. Detto, allora, ingrandimento visuale il rapporto
𝐼𝑉 =
tg(𝛽 ) 𝛿
= ,
tg(𝛼 ) 𝑓
si vede semplicemente che, per funzionare da lente di ingrandimento, è necessario che la lente in
esame abbia distanza focale 𝑓 sufficientemente piccola rispetto a 𝛿.
Tralasciando ora il campo dell’Ottica geometrica e passando a valutare l’incidenza del diametro
della pupilla sulla qualità della visione, è necessario soffermarsi sul fenomeno della diffrazione, il
quale risulta significativo qualora la radiazione incidente abbia lunghezza d’onda 𝜆 paragonabile
alle dimensioni di un ostacolo incontrato sul suo percorso; questo fenomeno, essendo legato alla
natura ondulatoria delle onde elettromagnetiche, è ovviamente ineliminabile. Nel caso dell’occhio
umano, la restrizione posta dalla pupilla (il cui diametro varia tra i limiti 𝐷1 ≅ 8𝑚𝑚 e 𝐷2 ≅ 2𝑚𝑚 a
seconda delle condizioni di illuminazione ambientale) è quella che si conosce studiando la
diffrazione da un foro circolare di diametro 𝐷. Sfruttando il teorema di Kirchhoff ed il principio di
Huygens-Fresnel, si può calcolare che l’angolo 𝜃 a cui cade il primo minimo di intensità della figura
di diffrazione(♣) è tale da soddisfare la relazione
sen(𝜃) = 1.22
𝜆
𝐷
In molte applicazioni tuttavia accade che 𝜆 ≪ 𝐷, per cui la precedente relazione può essere
riscritta in maniera linearizzata come
𝜃 ≈ 1.22
𝜆
,
𝐷
𝜆
→0
𝐷
2𝜃, allora, rappresenta la larghezza angolare del massimo centrale della figura di diffrazione.
Un aspetto notevole, che di fatto limita la risoluzione degli strumenti ottici in generale, è che
l’immagine di un punto data da una lente sia un dischetto. Questa osservazione è fondamentale
quando si vogliano distinguere due oggetti puntiformi, visti dalla lente sotto un angolo 𝛼 piccolo.
Se 𝛼 ≫ 𝜃 (oggetti molto spaziati angolarmente), allora non c’è sovrapposizione tra i due dischetti
che rappresentano le immagini degli oggetti: le due sorgenti si dicono risolte. Al diminuire di 𝛼,
invece, le figure di diffrazione cominciano a sovrapporsi. Esiste un angolo 𝛼𝑅 tale che il primo
minimo di diffrazione di una sorgente coincide col massimo principale dell’altra sorgente.
(♣)
N.B. Vale la pena di ricordare che, per ragioni di simmetria, la figura di diffrazione consta di un
disco luminoso centrale e di una serie di corone circolari alternativamente scure e chiare.
Caratteristiche fisiche dell’occhio umano
3
In questa situazione, le sorgenti si dicono appena risolte ed 𝛼𝑅 è detto angolo minimo risolvibile; il
suo reciproco,
𝜆 −1
𝐷
𝜌 = (𝛼𝑅 )−1 = �1.22 � =
,
𝐷
1.22𝜆
si dice potere risolutivo o separatore della lente.
Fatta questa necessaria digressione, si supponga di avere luce incidente di lunghezza d’onda nel
vuoto 𝜆 = 0.55𝜇𝑚 (luce gialla); è possibile calcolare i limiti di variabilità di 𝛼𝑅 in funzione del
diametro variabile 𝐷 della pupilla, ossia
(1)
(𝑖)
(2)
𝛼𝑅 ≅ 0.84 × 10−4 𝑟𝑎𝑑 < 𝛼𝑅 < 3.36 × 10−4 𝑟𝑎𝑑 ≅ 𝛼𝑅 ,
essendo 𝛼𝑅 = 𝛼𝑅 (𝐷𝑖 ), 𝑖 = 1, 2.
Posto un oggetto alla distanza 𝛿 ≅ 25𝑐𝑚 di visione distinta, la minima distanza 𝑠 tra due punti
ancora distinguibili dall’occhio nel caso più sfavorevole (𝐷 = 𝐷2 ≅ 2𝑚𝑚) vale
(2)
𝑠2 ≈ 𝛿𝛼𝑅 ≅ 84𝜇𝑚;
con 𝐷 = 𝐷1 ≅ 8𝑚𝑚, si trova 𝑠1 ≅ 21𝜇𝑚.
I fatti sperimentali, tuttavia, mostrano che l’angolo minimo risolvibile dall’occhio umano è più
vicino a 4 × 10−4 𝑟𝑎𝑑, per cui la minima distanza 𝑠 tra due punti distinguibili si attesta intorno al
valore di 100𝜇𝑚. Questa sovrastima del potere risolutivo discende da una carenza del modello
fisico adottato per spiegare il funzionamento dell’organo: infatti, non si tiene in alcun modo conto
della struttura granulare della retina, costituita da vari strati di cellule diverse che ricoprono la
parte posteriore del bulbo oculare, ricevono l’immagine formata dal cristallino e la inviano al
cervello mediante il nervo ottico. Tra le cellule della retina gli elementi sensibili alla luce sono di
due tipi: i coni ed i bastoncelli. Alla luce che attraversa il bulbo la retina si presenta dunque come
una sorta di superficie piastrellata dalle terminazioni di coni e bastoncelli, che in totale
assommano in un occhio a qualcosa come 125 milioni e le cui sezioni hanno diametri dell’ordine di
2𝜇𝑚. Pertanto, due punti sono visti come distinti qualora la luce da essi emessa colpisca due
sensori diversi: allora, non è sufficiente l’assunzione che i due dischetti (immagini dei punti
mediante la diffrazione) siano appena risolvibili, piuttosto occorre che questi abbiano raggio
paragonabile alla distanza tra i sensori; è questa la condizione che fissa la risoluzione.
In prossimità del collegamento del bulbo oculare al nervo ottico, sulla retina è presente una zona,
di diametro dell’ordine di 2𝑚𝑚, detta macchia lutea, in cui i coni sono predominanti rispetto ai
bastoncelli. L’accomodamento dell’occhio, quando si fissa un oggetto, tende a portarne
l’immagine al centro della macchia lutea, in una zona più sottile del resto della retina, detta fovea
(si veda la figura a pag. 1); in essa sono presenti esclusivamente coni ed in tal modo si realizza la
miglior acuità visiva possibile. Ciò che risulta veramente notevole è che la distanza tra due coni in
questa zona vale circa 10𝜇𝑚: pressoché la stessa misura del raggio dei dischetti di diffrazione
ottenuti con la pupilla aperta con diametro 𝐷2 ≅ 2𝑚𝑚. In altri termini, la granularità della retina è
Caratteristiche fisiche dell’occhio umano
4
corrispondente al potere risolutivo del cristallino, dal momento che due punti risolvibili producono
dischetti che interessano due sensori distinti. D’altra parte, quando sia 𝐷 = 𝐷1 ≅ 8𝑚𝑚, i dischetti
di due punti ancora risolvibili sono sì ridotti, ma sono anche più vicini tra loro e non colpiscono
sensori distinti: in questa diversa condizione di illuminazione la risoluzione del cristallino non trova
adeguata corrispondenza in quella della retina, che pertanto non distingue i due punti.
Infine, per quanto riguarda la capacità dell’occhio di distinguere i colori, si ritiene che la funzione
di reagire diversamente alle varie lunghezze d’onda sia demandata ai coni, piuttosto che ai
bastoncelli. Come è noto, la possibilità di distinguere i colori dipende anche dal grado di
illuminazione dell’oggetto (al crepuscolo tutti gli oggetti diventano grigi). I bastoncelli, che
veicolano un’immagine meno nitida, risultano particolarmente adatti alla visione crepuscolare,
essendo circa 4000 volte più sensibili alla luce dei coni, i quali invece presentano tre tipologie di
terminazioni nervose con sensibilità diversa per i tre colori fondamentali (rosso, verde, violetto).
Combinando le tre eccitazioni per questi colori, pesate coi rispettivi rapporti di intensità, nascono
le sensazioni per tutti i diversi colori.
Prima di concludere l’analisi fisica delle principali caratteristiche dell’occhio umano, è bene porre
un commento alla presenza all’interno di quest’ultimo di un vero e proprio diaframma, la pupilla,
che, come si è più volte ripetuto, è necessario a variare il flusso luminoso entrante, data l’evidente
impossibilità di modifiche all’assetto dei componenti ottici del sistema oculare. In effetti, la
presenza della pupilla, oltre a limitare l’apertura angolare dei fasci luminosi uscenti da oggetti
puntiformi posti sull’asse ottico, riduce anche le zone di spazio-oggetto i cui raggi possono essere
accettati dal sistema e trasformarsi in immagini: tali zone determinano il cosiddetto campo visivo.
Trascurando gli effetti della diffrazione, tutti i raggi uscenti da un oggetto puntiforme 𝑂 disposto
sull’asse ed interni ad un cono (in asse all’asse ottico) e la cui apertura (definita dal diametro della
pupilla) sia 𝛼, vengono accettati e trasformati in una immagine 𝑂′ puntiforme. L’immagine che
l’occhio forma della pupilla (d’entrata) si chiama pupilla d’uscita: tutti i raggi entranti nella pupilla
d’entrata escono dalla pupilla d’uscita, la quale è vista sotto l’angolo 𝛼′ dall’immagine 𝑂′.
A questo punto, si possono sviluppare delle semplici considerazioni legate alle proprietà
energetiche delle immagini. Infatti, preso un oggetto di area dσ piccola (ad esempio quadrato di
lato 𝑙), disposto perpendicolarmente all’asse ottico e che emetta luce in modo uniforme su tutta la
sua superficie, indicando con dΩ l’angolo solido sotto cui è vista la pupilla da parte dell’oggetto e
con 𝛼 la semiapertura del cono a sezione retta, avente l’oggetto come vertice e la pupilla come
base, si definisce la brillanza 𝐵 della sorgente l’energia luminosa d𝐸 che questa emette per unità
della sua superficie, per unità di tempo e per unità di angolo solido; in simboli
𝐵=
d𝐸
dσd𝑡dΩ
In analogia si definisce la brillanza 𝐵′ dell’immagine (considerando ovviamente la pupilla d’uscita).
Se si suppongono trascurabili le perdite di energia per riflessione e assorbimento, si ha che la
quantità di energia che esce nell’unità di tempo dalla sorgente ed entra nella pupilla arriva
inalterata sull’immagine; ciò permette di scrivere
Caratteristiche fisiche dell’occhio umano
5
d𝐸
= 𝐵dσdΩ = 𝐵′dσ′dΩ′
d𝑡
Tenuto conto che, per quanto ipotizzato, dσ = 𝑙 2, dσ′ = 𝑙′2, dΩ ≅ 𝜋𝛼 2 , dΩ′ ≅ 𝜋𝛼′2 e che vale la
cosiddetta formula di Lagrange
𝑛𝛼𝑙 = 𝑛′ 𝛼 ′ 𝑙 ′ ,
essendo 𝑛 ed 𝑛′ gli indici di rifrazione dei mezzi che contengono le superfici dσ e dσ′
rispettivamente, si ha finalmente
𝐵𝑙 2 𝜋𝛼 2 = 𝐵′ 𝑙′2 𝜋𝛼′2 ⟺
𝐵
𝐵′
= 2
2
𝑛
𝑛′
Allora, nell’ipotesi che la trasparenza sia perfetta e che non ci siano dispersioni di energia per
assorbimento, la brillanza dell’oggetto sta in un rapporto, definito dagli indici di rifrazione 𝑛 ed 𝑛′,
con la brillanza dell’immagine. Nel caso in cui, come usualmente accade, una parte non
trascurabile dell’energia luminosa venga dispersa nel sistema ottico, l’ultima relazione scritta è da
leggersi in verità come un diseguaglianza; ovvero
2
𝑛′
𝐵′ < � � 𝐵
𝑛
Insomma, la brillanza è una quantità invariante per sistemi ottici ideali (senza dispersioni, né
riflessioni); nel caso tale approssimazione non rispecchi la realtà, si vede che la brillanza può
soltanto diminuire. Se anche si riesce a concentrare la luce su di una piccola area, si osserva
simultaneamente un aumento della divergenza angolare (e viceversa). Questa ultima osservazione
è, di fatto, coerente con il Teorema di Liouville, formulato spesso per sistemi meccanici, ma la cui
validità è tutt’altro che limitata a questi, prestandosi evidentemente a notevoli generalizzazioni.
Vincenzo Ventriglia
Caratteristiche fisiche dell’occhio umano
6