TRIGONOMETRIA
“Trigonometria” è una parola che deriva dal greco: significa “misura dei triangoli”. Studiando la
trigonometria vedremo l’utilità della goniometria in diversi campi applicativi: geometria piana e solida, fisica, topografia, ecc.
In questa lezione affronteremo i seguenti argomenti:
1) Risoluzione dei triangoli (rettangoli e qualunque)
2) Area del triangolo
3) Teorema dei seni
4) Teorema del coseno.
Risoluzione dei triangoli, per adesso rettangoli
“Risolvere un triangolo” significa determinare tutti gli elementi di un triangolo (i tre lati e i tre angoli interni) conoscendo, come dati iniziali, solo alcuni di essi.
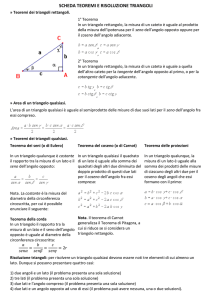
Facciamo un passo indietro e pensiamo al teorema di Pitagora. Il teorema di Pitagora riguarda solamente i triangoli rettangoli: conoscendo la lunghezza di due lati di un triangolo rettangolo, si riesce a determinare la lunghezza del terzo lato.
C
γ
a
b
α
A
β
c
B
Ad esempio, se conosciamo la lunghezza dei due cateti, AB e AC , possiamo calcolare la lunghezza
dell’ipotenusa, BC :
2
2
2
2
BC = AB + AC
oppure, conoscendo la lunghezza di un cateto, AB , e dell’ipotenusa, BC , possiamo calcolare la
lunghezza dell’altro cateto, AC :
AC = BC − AB .
Usando la trigonometria riusciremo a fare molto di più: conoscendo la lunghezza di due lati di un
triangolo rettangolo riusciremo a calcolare non solo la lunghezza del terzo lato (potremo usare benissimo di teorema di Pitagora) ma anche l’ampiezza dei due angoli acuti del triangolo. In realtà noi
già sappiamo che se i due cateti sono congruenti, allora i due angoli acuti sono di 45° dato che il
triangolo è rettangolo ma anche isoscele. Inoltre, se il rapporto tra due cateti è pari a 3 , ossia se il
secondo cateto si ottiene moltiplicando il primo per 3 , o ancora, se AB : AC = 3 : 1, allora
l’angolo acuto adiacente al cateto minore è di 60° e l’angolo acuto adiacente al maggiore è di 30°.
Questo secondo caso, dei due angoli acuti di 30° e di 60°, corrisponde anche al caso in cui uno dei
due cateti è la metà dell’ipotenusa. Ad ogni modo, è il caso della squadra (da disegno) cosiddetta
30-60. Salvo questi due casi particolari, per trovare le ampiezze degli angoli acuti occorre usare la
trigonometria.
Le regole da ricordare sono (dicendo angolo adiacente ad un cateto si intenderà l’angolo acuto, non quello retto):
cateto2 = cateto1 × tangente(angolo adiacente a cateto1) È la regola del campanile
cateto2 = cateto1 × cotangente(angolo adiacente a cateto2)
cateto = ipotenusa × cos(angolo tra ipotenusa e cateto)
cateto = ipotenusa × sen(angolo opposto al cateto)
Queste regole si possono scrivere così:
b = c ⋅ tgβ
c = b ⋅ tgα
c = a ⋅ cos β
b = a ⋅ cos γ
1
c = a ⋅ senγ
b = a ⋅ senβ
Si noti che la tangente e la cotangente entrano in gioco quando si lavora con i due cateti mentre il coseno e il seno entrano in gioco quando si lavora con un cateto e l’ipotenusa.
Occorre imparare bene le precedenti 6 relazioni: se non si conoscono bene a memoria è inutile procedere nello studio! N.B.: non abbiamo riscritto in simboli quella della cotangente perché se si imparano bene quelle della tangente si è a posto in quanto si possono sempre ricavare quelle della
cotangente ricordando che:
la tangente di β è uguale alla cotangente di γ e viceversa
Per utilizzare in modo proficuo le 6 relazioni precedenti, occorre anche saperle invertire. Ad esempio, invertendo la prima relazione, possiamo calcolare l’ampiezza dell’angolo β , una volta note le
b
b
lunghezze dei lati b e c. Infatti: tgβ = , da cui β = arctg . Come esercizio, molto importante,
c
c
prova a invertire tutte le altre cinque relazioni, determinando l’angolo utilizzando le funzioni arctg,
arcsen e arccos.
Vediamo un esercizio in cui mettiamo in pratica ciò che
C
abbiamo imparato:
γ
1) Dati: α = 30° , β = 45° , CH = 12
Si trova:
β
α
AB = AH + HB = CHcotg α +CHcotg β ; (32,78)
A
B
H
γ = 180° − 30° − 45° ; (105°)
AC = AH/cos α (o col teorema di Pitagora) (24)
BC = HB/cos β (o col teorema di Pitagora) (16,97)
2) Dati: α = 60° , HB = 9 , cos β = 1 / 3
Si trova:
2
2
CB = HB/cos β da cui CH = CB − HB quindi AH = CHcotg α . Allora AB = AH + HB
Inoltre AC = AH/cos α
E per gli angoli incogniti, si ha: β = arccos(1 / 3) γ = 180° − α − β .
3) Dati: AC = 24, β = 60° , tg α = 4/3.
Si trova: α = arctg(4 / 3) , AH = ACcos α , CH = ACsen α , HB = CH/tg β , AB = AH + HB,
CB = HB/cos β , γ = 180° − α − β .
4) Dati: CH = 8, AH = 6, β = 30° . Fai da solo: trova AB, BC, AC, α e γ .
Imparando bene le relazioni precedenti potremo “risolvere” non solo i triangoli rettangoli ma anche
i triangoli qualunque. Per fare ciò avremo però bisogno anche di due importanti teoremi: il teorema
dei seni e il teorema del coseno, che studieremo tra poco.
Area del triangolo
Dato un triangolo qualsiasi, conoscendo la lunghezza di due lati a e b e dell’ampiezza dell’angolo
compreso tra essi, γ , possiamo calcolare l’area A del triangolo:
1
A = ab ⋅senγ
b
2
Il motivo è semplice: l’area è data da base × altezza diviso 2. Oγ
ra, la base è a, l’altezza è bsen γ , quindi: Area = a × bsen γ : 2.
a
2
Teorema dei seni
Si capisce che l’altezza si può ottenere sia con c ⋅ senα che con a ⋅ senγ , quindi:
β
a
c
γ
α
b
a
c
=
senα senγ
Considerando anche le altre altezze relative ai lati a e c si ota
b
c
b
tengono anche le relazioni:
e
=
=
senα senβ
senγ senβ
Mettendo insieme il tutto abbiamo il teorema dei seni:
a
b
c
=
=
senα senβ senγ
c ⋅ senα = a ⋅ senγ , il che vuol dire:
A cosa serve il teorema dei seni? Ne vedremo l’utilità nella “risoluzione” di un triangolo qualunque.
senβ
L’importante è capire che bisognerà sapere anche invertire le relazioni. Ad esempio: b = c ⋅
,
senγ
a ⋅ senβ
(e quindi α = arcsen(a ⋅ senβ / b)) .
oppure senα =
b
Teorema del coseno
È un teorema davvero interessante! Praticamente è l’estensione del teorema di Pitagora ad un triangolo qualunque: si può trovare un lato conoscendo gli altri due e l’angolo tra essi compreso.
Supponiamo di conoscere a e b oltre all’angolo γ . Dopo aver disegnato l’altezza h relativa al maggiore tra a e b, e suddiviso b in due parti b’ e b”,osserviamo che:
β
a
c = b '2 + h 2
c
h
Ma b’ = b – b” = b – acos γ e h = asen γ . Allora, sostituendo:
α b’
b” γ
c = (b − a cos γ )2 + (asenγ )2 = b 2 − 2ab cos γ + a 2 cos 2 γ + a 2sen 2 γ =
b
(
)
b 2 − 2ab cos γ + a 2 cos 2 γ + sen 2 γ = a 2 + b 2 − 2ab cos γ
E quindi abbiamo: c = a 2 + b 2 − 2ab cos γ
Osserva che per γ = 90°, il coseno è 0 e si ottiene il solito teorema di Pitagora!
Ovviamente abbiamo delle formule analoghe per gli altri due lati. Scrivile per esercizio! (osserva
che l’angolo sotto radice è sempre quello opposto al lato da trovare).
Se conosciamo a, b e c, invertendo le formule, possiamo trovare gli angoli:
⎛ a 2 + b2 − c2 ⎞
⎟
γ = arccos⎜
⎜
⎟
2
ab
⎝
⎠
⎛ a 2 + c2 − b2 ⎞
⎟
β = arccos⎜
⎜
⎟
2
ac
⎝
⎠
⎛ b2 + c2 − a 2 ⎞
⎟
α = arccos⎜
⎜
⎟
2
bc
⎝
⎠
Siamo quindi pronti per affrontare la
Risoluzione di un triangolo qualunque
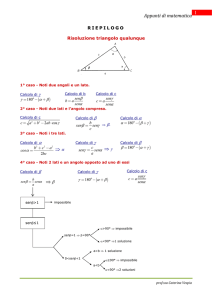
Possiamo ricavare tutti gli altri elementi se ne conosciamo tre, di cui almeno uno, deve essere un lato.
1) Noti i tre lati: a, b e c.
Invertendo
il teorema del coseno, possiamo trovare γ e, sempre col
β
a
c
teorema del coseno, oppure col teorema dei seni, possiamo trovare
γ
α
b
3
α (oppure β ). Se conosciamo due angoli, il terzo si trova sotraendo la loro somma da 180°.
2) Noti due lati e un angolo. Ci sono due casi:
1° caso) a, b e γ (due lati e l’angolo tra essi compreso):
Col teorema del coseno troviamo c e poi, conoscendo ora tutti i lati procediamo come già visto.
2° caso) a, b e α (oppure β ) (due lati e uno degli angoli non compresi tra i lati)
Col teorema dei seni posso trovare β . Ora possiamo trovare γ (= 180° − α − β ) e, col teorema del
coseno, da a, b e γ troviamo anche c.
3) Noti un lato e due angoli. Troviamo il terzo angolo per differenza da 180°. Col teorema dei seni
possiamo ora trovare un secondo lato e il terzo lato lo si trova applicando o ancora il teorema dei
seni o il teorema del coseno.
4