Equazioni di Maxwell e propagazione radio

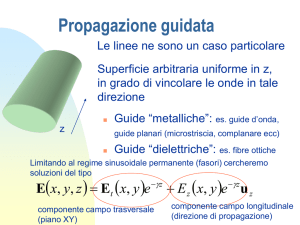
Equazioni di Maxwell, Propagazione
radio, Materiali conduttori e dielettrici
brevi note raccolte da
Davide Micheli
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
1
Agenda:
• Equazioni di Maxwell e propagazione per onde elettromagnetiche piane
nel vuoto
• Unità di misura logaritmiche nelle trasmissioni radio
• Definizione dell’attenuazione di tratta per un collegamento radio
• Propagazione dei segnali radio nella ionosfera, applicazione al caso
dei segnali provenienti da satelliti per il servizio GPS
• Superfici selettive in frequenza
• Linee di Trasmissione
• Conduttori e Dielettrici
• Conduzione elettrica dal punto di vista atomico
• Propagazione Libera
• Note sulla matrice di Scattering (Diffusione) nelle trasmissioni a
microonde
• Generalità sulle Guide D’onda Metalliche
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
2
Breve storia
James Clerk Maxwell (13 giugno 1831 - 5 novembre 1879) fu il fisico scozzese del XIX secolo elaborò la
prima teoria moderna dell'elettromagnetismo compendiando in poche equazioni tutte le nozioni di questa
scienza. Maxwell tuttavia rimase legato ad una concezione di campo elettromagnetico la cui propagazione
avviene attraverso un mezzo etereo; dapprima egli identificò l'etere luminifero con quello elettromagnetico e
poi unificò i due fenomeni, quelli ottici e quelli elettromagnetici, infatti dalle sue equazioni tali onde sono
immediatamente deducibili.
Maxwell eresse il suo monumento alla scienza partendo dalle basi gettate da illustri scienziati tra cui non
possiamo dimenticare il grande chimico-fisico sperimentale Michael Faraday e il fisico teorico Ampère.
Inoltre Maxwell è anche noto per i suoi lavori effettuati nel campo della meccanica sui criteri di resistenza, in
particolare nel 1856 propose il così detto: "Criterio della massima energia di distorsione".
Tra i 16 e i 19 anni studia letteratura e filosofia presso William Hamilton e poi si iscrive all'università di
Cambridge. Nel '50 conosce Stokes e pubblica un lavoro, Equilibrio dei solidi elastici, nel quale ricava le
equazioni di Stokes e le applica a casi concreti per conoscere le proprietà fisiche della materia, mostrando la
sua indole di uomo pratico della rivoluzione industriale. Sempre a Cambridge conosce Whewell e ne studia la
filosofia. Nello stesso anno si realizza l'incontro con William Thomson (poi Lord Kelvin) che avrà grande
rilevanza sulla formazione del giovane Maxwell e avrà importanti risvolti per la sua attività di ricerca. Tra i tanti
personaggi le cui ricerche e le cui interazioni con Maxwell hanno fornito una base e man mano un aiuto per
elaborazione dell'elettromagnetismo, due sembrano essere state le figure più luminose: Thomson e Faraday.
Le principali linee guida del pensiero di Maxwell sono identificabili in ricerca dell'unità (unificazione)
rifiuto di ipotesi microscopiche enfasi sui risultati sperimentali.
Come metodo di indagine teorica Maxwell premia quello dell'analogia come il migliore perché è in grado di
gettar luce su campi della scienza meno noti, partendo dalle leggi che governano fenomeni meglio conosciuti.
Tuttavia questo metodo, sebbene efficace, dev'essere usato con consapevolezza per non vanificare gli sforzi
trasformando utili aiuti in fuochi fatui ("useful helps into Wills of the Wisp", da "Essey for the Apostles on
Analogies in Nature").
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
3
CONCETTO DI CAMPO ELETTRICO
Fenomeni Stazionari ( grandezze nel sistema MKS)
La forza cui sono soggette due cariche elettriche puntiformi nel vuoto è:
r
r
1 q1q2
q1q2
F=
rˆ = k 2 rˆ dove F si misura in
2
4πε0 r
r
q1
r
q2
k=
1
4πε0
= 9⋅109
⎡ Nm2 ⎤
⎢ 2 ⎥
⎣C ⎦
ε0 = 8.854⋅10−12
[N]
⎡ C2 ⎤
⎢ 2⎥
⎣ Nm ⎦
Il Coulomb è definito come quella carica che attraversa in un secondo un
conduttore percorso dalla corrente di un Ampere.
Data una carica Q ferma nello spazio, allora se una seconda carica q viene posta,
ferma, in presenza della prima, essa subisce una forza dipendente dalla posizione
occupata q; ed in modulo proporzionale a q .
Il rapporto tra la forza F e la carica q viene detto Campo Elettrico generato nella
posizione r dalla carica Q:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
4
CONCETTO DI CAMPO ELETTRICO
r
r F ⎛ 1 Qq ⎞ 1
Q
⎟
ˆ
rˆ
=
r
k
E = = ⎜⎜
2
2
⎟
r
q ⎝ 4πε0 r ⎠ q
r
⎡ N ⎤ ⎡ N m ⎤ ⎡ J 1 ⎤ ⎡V ⎤
=⎢
=⎢ ⎥
dove E si misura in ⎢ ⎥ = ⎢
⎥
⎥
⎣ C ⎦ ⎣ C m ⎦ ⎣C m ⎦ ⎣ m ⎦
Il campo elettrico può avere linee di flusso entranti o uscenti a seconda del
segno della carica Q, per convenzione si pone:
Q
+
q
r
Davide Micheli
-
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
5
CONCETTO DI CAMPO ELETTRICO
Per la rappresentazione grafica dei campi è usuale l’uso delle linee di forza.
Le linee di forza sono linee di flusso tali che in ogni punto il campo elettrico è
tangenziale alle linee di forza.
In ogni regione del campo viene disegnato un numero di linee di forza tale che
la loro densità sia proporzionale all’intensità del campo.
bisogna precisare che la carica q di prova deve essere abbastanza piccola da
produrre una perturbazione trascurabile nella configurazione delle cariche Q
circostanti che generano il campo, più precisamente deve risultare:
r
rr
F
E(r ) = lim
q→0 q
Si può interpretare questa situazione supponendo che la carica Q modifichi lo
spazio ad essa circostante, producendo nel punto occupato dalla carica q,
uno stato fisico, che chiamiamo campo di forza elettrico, a causa del quale q
subisce una forza proporzionale alla sua carica e inversamente proporzionale
al quadrato della distanza.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
6
CONCETTO DI CAMPO ELETTRICO
Supponendo vera questa ipotesi si può concludere che l’intensità del campo
elettrico in un punto individuato da r è indipendente dal fatto che esista o
meno la carica q; l’esistenza del campo è infatti legata alla presenza della
sorgente Q e non a quella della carica sul quale il campo agisce.
Il concetto di campo è utile perché elimina la necessità di ricorrere all’ipotesi
di azioni a distanza fra particelle; tuttavia occorre precisare che finchè si
rimane in condizioni statiche, come quelle considerate (particelle ferme), le
due descrizioni: azione a distanza o azione locale del campo sono del tutto
equivalenti.
E’ soltanto in condizioni dinamiche che l’esistenza del campo acquista un
significato fisico indipendente dalle cariche sulle quali agisce, in quanto si
manifestano fenomeni fisici legati alla presenza del campo anche nello spazio
privo di materia.
Da notare che uno spazio privo di materia ma sede di un campo (elettrico,
magnetico, gravitazionale) non è uno spazio vuoto in quanto è possibile
associare al campo quantità fisiche misurabili come energia e quantità di
moto.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
7
CONCETTO DI CAMPO ELETTRICO
Inoltre, e questo è molto importante, poiché l’interazione tra due particelle
separate spazialmente non è mai istantanea (in quanto la velocità di
propagazione non è infinita), la forza che agisce su una particella dipende
dalla posizione dell’altra in un istante precedente;
Si osserva sempre un ritardo fra l’istante in cui cambia la forza agente su una
particella e l’istante in cui cambia la posizione dell’altra particella, ritardo che
il campo impiega a propagarsi da una particella all’altra.
Gli effetti prodotti dalle cariche sorgenti, possono manifestarsi con intensità
significativa, anche in porzioni di spazio molto lontane da quelle occupate
dalle cariche sorgenti; ed il ritardo con cui tali effetti si manifestano può
essere interpretato in termini del tempo che il campo impiega a propagarsi
nello spazio.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
8
DIPOLO ELETTRICO
La più semplice tra le configurazioni di carica è:
z
z
Q
Q
+
+
+
-
Le linee di forza nello spazio si ottengono per rotazione intorno all’asse z
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
9
DIPOLO ELETTRICO
Lo studio delle azioni elettrostatiche subite da un dipolo elettrico, è di
particolare rilievo perché ad esse sono riconducibili le interazioni
elettrostatiche più semplici cui sono soggetti i sistemi microscopici
elettronicamente neutri (atomi e molecole non ionizzati).
Ogni dipolo elettrico è caratterizzato da una grandezza detta momento di
dipolo:
v v
P = rq
q1
-
r
q2
+
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
10
CONCETTO DI CAMPO MAGNETICO
FENOMENI STAZIONARI
L’esistenza di forze magnetiche porta alla introduzione di un campo vettoriale,
detto campo magnetico, analogo al campo elettrico. Tuttavia il campo
magnetico presenta caratteristiche sostanzialmente diverse da quelle del
campo elettrico; ciò è conseguenza del fatto che mentre esistono cariche
elettriche positive separate da quelle negative, non è per contro possibile
separare monopoli magnetici.
N
N
Rompendo una calamita
si formano due calamite,
sempre con due poli
S
N
N
S
S
N
S
N
S
N
S
S
N
S
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
11
CONCETTO DI CAMPO MAGNETICO
Queste differenze hanno come conseguenza che le linee di flusso del campo
magnetico sono sempre linee chiuse, ovvero il flusso uscente da una
qualunque superficie chiusa è nullo.
Viceversa nel caso del campo elettrico le linee di forza escono dalle cariche
positive (sorgenti del campo) e finiscono sulle cariche negative (pozzi del
campo).
Tale differenza è osservabile dal momento che le forze subite dall’ago
magnetico della bussola ha l’andamento tipico dell’azione subita da un dipolo
e non da azioni subite da cariche puntiformi.
In particolare un ago magnetico si dispone all’equilibrio, parallelamente al
campo, cosicché con la sua direzione esso individua in ogni punto la tangente
alle linee di forza del campo magnetico.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
12
CONCETTO DI CAMPO MAGNETICO
Un passo decisivo per la comprensione dei fenomeni magnetici è
l’osservazione di Oestered (1820), secondo cui un filo percorso da corrente
genera, su un ago magnetico esploratore, effetti orientanti analoghi a quelli
esercitati da una calamita.
In altri termini un filo percorso da corrente elettrica genera un campo
magnetico.
Nell’ambito di uno studio sistematico ( compiuto fra gli altri da Coulomb, Biot,
F.Savart, Faraday, Lorents, Ampere, Maxwell) fu evidenziata l’esistenza di
mutue azioni meccaniche fra fili percorsi da corrente.
Poiché le correnti elettriche sono definite in termini di cariche in movimento:
I=dQ/dt
tutti i fenomeni magnetici furono così ricondotti ad una comune base secondo
cui essi sono generati in relazione al movimento di cariche; anche le azioni fra
materiali magnetici sono interpretabili in termini di movimento di cariche
microscopiche che sono le correnti atomiche.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
13
CAMPO MAGNETICO: forza do Lorents
Si può sintetizzare ipotizzando che i circuiti percorsi da corrente generino nel
loro intorno un campo B che chiameremo di induzione magnetica dipendente
dalla posizione, il quale determina sul tratto dl percorso da corrente I ed
orientato secondo il verso di circolazione di I una forza espressa dalla legge:
r r
r
dF = Id l × B
r
r
r
dF = dNq vd × B
r r r r
r r r
r
ma : Id l = j ds dl = nq vd ds dl = dNq vd
nr = particelle per unità di volume
B = campo di induzione magnetica
Ir = corrente elettrica
rj = densità di corrente
v d = velocità di deriva delle cariche elettriche r
dN = numero di portatori presenti nel tratto dl
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
14
CAMPO MAGNETICO: forza do Lorents
Pertanto ci si aspetta che una singola carica puntiforme che si muova con
velocità v nel campo di induzione magnetica B subisca una forza detta forza di
Lorents pari a:
F
r r r
F = qV × B
B
V
Secondo tale eq, una carica ferma con v=0 rispetto al riferimento del campo B,
non è soggetta ad alcuna forza ad opera di un campo magnetico, mentre
quando si muove, essa è sottoposta ad una forza ortogonale alla sua velocità
v . Le dimensioni fisiche del vettore induzione magnetica sono:
⎤
⎡
forza
⎡
⎤ ⎢ N 1 ⎥ ⎡ N m s ⎤ ⎡ J s ⎤ ⎡V s ⎤ ⎡Wb⎤
=⎢
=⎢
=⎢
=⎢
= ⎢ 2 ⎥ = [T ]
B≡⎢
⎥
⎥
⎥
⎥
⎥
⎣carica⋅ velocità⎦ ⎢ C m ⎥ ⎣ C m m⎦ ⎣Cm m⎦ ⎣ m m⎦ ⎣ m ⎦
⎣ s⎦
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
15
CAMPO MAGNETICO: forza do Lorents
Dunque un Tesla (1T) è un campo di induzione magnetica B tale che una
carica di un Coulomb, in moto con velocità di un 1m/s, è soggetta alla forza di
un N se tale velocità è ortogonale a B.
Se in una certa regione dello spazio agisce oltre al campo di induzione
magnetica B (le cui sorgenti sono correnti elettriche) anche un campo elettrico
E (le cui sorgenti sono cariche elettriche)
Allora una particella carica q è sottoposta alla forza:
r r r r
F = qE + qv × B
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
16
CAMPO MAGNETICO: forza do Lorents
Considerando un circuito filiforme l’ percorso da corrente I; allora si trova
sperimentalmente che il campo di induzione magnetica B generato nello
spazio circostante è dato dalla 1° eq di Laplace:
r µ0 dl ' × ∆rr
dB0 =
I
r3
4π
∆r
⎡Ω⋅ s ⎤
−7 ⎡ Henry⎤
con µ0 = 4π ⋅10 ⎢
= 4π ⋅10 ⎢
⎥
⎣ m ⎥⎦
⎣ m ⎦
−7
è la permeabilità magneticadel vuoto
dl’
z
∆r=r-r’
dB0(P)
r’
I
P(x,y,z)
r
y
x
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
17
CAMPO MAGNETICO: forza do Lorents
In particolare in base alla precedente si può trovare che una spira circolare di
raggio R percorsa da corrente I stazionaria, genera in un punto P del suo asse
un campo di induzione magnetica B0 pari a:
r µ0I
B0 =
nˆ
2R
I
n
R
y
x
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
18
Induzione elettromagnetica Legge Faraday Neumann
Consideriamo un circuito (a) costituito da una linea chiusa l realizzata mediante
un filo conduttore.
Disponiamo in serie al circuito un galvanometro G mediante il quale è possibile
constatare l’eventuale passaggio di corrente in (a).
Si riscontra sperimentalmente che il galvanometro indica passaggio di corrente
nei seguenti casi:
1) chiusura del tasto T
L
G Ia≠0
(a)
f
Davide Micheli
I
T
(b)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
19
Induzione elettromagnetica Legge Faraday Neumann
2) ll circuito (b) si sposta dal circuito (a) con velocità vb per esempio in modo
armonico
L
G Ia≠0
I
Vb
(a)
(b)
f
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
20
Induzione elettromagnetica Legge Faraday Neumann
3) Il magnete permanente (b) si sposta dal circuito (a) con velocità vb per
esempio in modo armonico
N
L
G Ia≠0
Vb
(a)
S
(b)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
21
Induzione elettromagnetica Legge Faraday Neumann
Faraday spiegò queste ed altre analoghe osservazioni sperimentali dicendo:
Se un circuito è immerso in un campo di induzione magnetica il cui flusso Ф(B)
concatenato con il circuito stesso sia variabile nel tempo, allora in esso si
genera una forza elettromotrice indotta data da:
r
dΦ(B)
d r r
findotta= −
= − ∫ B⋅ ds
dt
dt S
B(t)
Ii(t)
Bi(t)
Quando nel circuito si genera una forza elettromotrice indotta da un campo di
induzione magnetica B variabile, concatenato con il circuito stesso, allora in
esso circola corrente.
Questa corrente genera a sua volta un campo magnetico indotto Bi il cui flusso
concatenato con il circuito è diverso da zero.
Il segno meno davanti al secondo membro indica che il flusso del campo
magnetico indotto Bi, concatenato con il circuito, tende a compensare la
variazione di flusso responsabile del fenomeno di induzione stesso.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
22
Induzione elettromagnetica: Legge di Lents
Questa legge conosciuta come legge di Lents afferma che: il verso della forza
elettromotrice indotta, è tale da opporsi alla variazione di flusso che la genera
Si consideri un circuito elettrico in condizioni stazionarie; cioè tale che il
tempo impiegato dai segnali elettromagnetici per attraversarlo sia molto
piccolo rispetto al tempo che caratterizza le variazioni di densità carica ρ e
densità di corrente j. Ovvero all’istante (t) la correnti I(t) è la stessa in tutti i
punti del circuito.
B
I(t)
B
≈ f
I(t)
Iai(t) ≈ f
Bai
Tale corrente genera nello spazio circostante un campo di induzione magnetica
B diverso da zero.
Se I(t) varia nel tempo vara parimenti B(t) e quindi anche Ф(B): si genera
pertanto una forza elettromotrice autoindotta che si oppone alla forza
elettromotirce responabile di B(t)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
23
Induzione elettromagnetica: Induttanza L
r
'
r
µ0 dl × ∆r
dB0 =
I
r3
4π
∆r
⇒
r
'
r
µ0
dl × ∆r
B0 =
I (t )
r3
∫
4π l
∆r
Osservando la I formula di Laplace scritta sopra si nota che:
B è proporzionale ad I(t);
Ф(t) concatenato con il circuito è proporzionale a B
Pertanto segue che Ф(t) è proporzionale a I(t):
r⎤
r⎤ ⎫
'
'
⎧
⎡
⎡µ
r
r r
r ⎪ µ0 dl × ∆r
r⎪
dl × ∆r
0
Φ( B) = L ⋅ I = ∫ B ⋅ ds = ∫ ⎢ ∫ I (t )
⎥ ⋅ ds ⎬I (t )
⎥ ⋅ ds = ⎨∫ ⎢ ∫
r
r
3
3
∆r ⎥⎦
⎪⎩ S ⎢⎣ 4π l ∆r ⎥⎦ ⎪⎭
S
S ⎢
⎣ 4π l
Il coefficiente di poporzionalità L è definito coefficiente di autoinduzione o
induttanza del circuito stesso
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
24
Induzione elettromagnetica: Induttanza L
Il valore dell’induttanza L è determinato unicamente dalla geometria del
circuito e dal materiale utilizzato.
Nel sistema internazionale si misura in:
⎡ Weber ⎤ ⎡V ⋅ s ⎤
L=⎢
=⎢
= [Ω ⋅ s ] = [Henry ]
⎥
⎥
⎣ Ampere ⎦ ⎣ A ⎦
Dalla legge di Faraday segue che:
f indotta
r
dΦ( B)
d (L ⋅ I (t ) )
dI
=−
=−
= −L
dt
dt
dt
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
25
I) equazione di Maxwell
Consideriamo il teorema di GAUS:
Il flusso del campo elettrostatico E0 attraverso una qualunque superficie
chiusa S, è pari alla somma algebrica delle cariche contenute all’interno di S,
divisa per la costante ε0. Eventuali cariche disposte esternamente alla
superficie non portano alcun contributo al flusso di E0 .
S
ds
n
r
r v 1
1
Φ(E0 ) = ∫ E0 ⋅ ds = ∑qint. = ∫ ρ(x, y, z, t)dτ
ε0
S
ε0 τ
La sommatoria si riferisce ad una distribuzione di carica discreta; mentre
l’integrale di volume su τ si riferisce a duna distribuzione di carica continua
con densità:
ρ=
Davide Micheli
nq
τ
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
26
I) equazione di Maxwell
Dal
teorema
divergenza:
della
(
)
r v
r
∫ E0 ⋅ ds = ∫ ∇ ⋅ E0 dτ
τ
S
⇓
r
r v
r
1
Φ( E0 ) = ∫ E0 ⋅ ds = ∫ ∇ ⋅ E0 dτ = ∫ ρ ( x, y, z)dτ
(
τ
S
)
ε0 τ
⇓
r
1
∇ ⋅ E0 = ρ ( x, y, z)
ε0
L’eguaglianza degli integrandi segue dal teorema di Gaus che vale per
qualunque superficie chiusa S di integrazione e dunque anche per qualunque
volume di integrazione in essa racchiuso.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
27
I) equazione di Maxwell
Per la validità è necessario che le grandezze siano continue ed il campo
derivabile in ogni punto con continuità altrimenti occorre applicare tale
equazione locale in ogni punto usando eventualmente le condizioni di
raccordo:
Et1=Et2 ; Dn1=Dn2 con D=εE
cioè ε1E1= ε2E2
Si osserva che il teorema di Gauss collega tra loro grandezze fisiche calcolate
in posizioni diverse: il campo elettrico sulla superficie S alla densità di carica
ρ in punti interni alla superficie S stessa.
Questo non è un problema fino a che le grandezze in gioco sono costanti nel
tempo; tuttavia la generalizzazione al caso non stazionario non è immediata,
considerato che una eventuale variazione di carica nel tempo, ad esempio
della densità ρ(x,y,z) dentro la superficie non può tradursi in una simultanea
variazione del campo elettrico sulla superficie in quanto nessun fenomeno
fisico si propaga con velocità infinita.
Al contrario la 1° equazione di Maxwell lega fra loro grandezze fisiche diverse
calcolate nella stessa posizione.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
28
I) equazione di Maxwell
Essa si presta pertanto alla immediata generalizzazione al caso non
stazionario introducendo semplicemente la dipendenza dal tempo delle
grandezze che il essa compaiono:
I)
Davide Micheli
r 1
∇⋅ E0 = ρ(x, y, z, t)
ε0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
29
II) equazione di Maxwell
Applicando l’operatore divergenza alla formula di Laplace:
r
'
r µ0
dl ×∆r
B0 = ∫ I (t) r 3
4π l
∆r
Si trova che:
II)
r
∇⋅ B = 0
Che si enuncia dicendo che il vettore B0 è solenoidale, come conseguenza si
ricava la proprietà di B0 :
Sia S una qualunque superficie chiusa, e sia τ il volume in essa racchiuso,
allora il flusso del campo di induzione magnetica B0 attraverso una qualunque
superficie chiusa è nullo;
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
30
II) equazione di Maxwell
r r
r
Φ s ( B0 ) = ∫ B0 ⋅ ds = ∫ (∇ ⋅ B0 )dτ = 0
S
ds
τ
S
n
Si è applicato il teorema della divergenza:
l
r r
r
∫ B0 ⋅ ds = ∫ (∇⋅ B0)dτ
S
τ
Ovvero sia anche il flusso di B0 attraverso due superfici S e S’ aventi lo
stesso contorno l e orientamento discorde è uguale ed opposto.
ds
n
l
n1
ds1
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
31
II) equazione di Maxwell
Tenendo conto che cambiando il verso di orientamento delle superfici il
flusso cambia segno si ottiene allora immediatamente l’altra proprietà spesso
usata:
ds
n
n1
ds1
l
Il flusso di B0 attraverso due superfici qualunque aventi lo stesso contorno ed
orientamento concorde è uguale, per cui si può parlare semplicemente di
flusso concatenato con quel contorno;
Se il contorno l rappresenta una spira allora il flusso Ф(B) si dice concatenato
con quella spira.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
32
II) equazione di Maxwell
Si consideri per semplicità una superficie come quella indicata in figura:
n1
v r
v r
v r
v r
Φ( B) = ∫ B ⋅ ds = ∫ B ⋅ ds1 + ∫ B ⋅ ds2 + ∫ B ⋅ ds3 = 0
s1
S
s3
S2
S3
n3
ds3
s2
S1
Poiché in un circuito magnetico il vettore induzione
magnetica si dispone parallelamente alla superficie
ne consegue che:
v
v r
Φ3(B) = ∫ B⋅ ds3 = 0
S3
n2
Pertanto:
v r v r
v r
Φ(B) = ∫ B⋅ ds = ∫ B⋅ ds1 + ∫ B⋅ ds2 = 0
S
Davide Micheli
S1
S2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
33
II) equazione di Maxwell
Impostando quindi il verso di n2 come quello negativo entrante si ottiene:
n1
v r
v r
v r
Φ( B) = ∫ B ⋅ ds = ∫ B ⋅ ds1 − ∫ B ⋅ ds2 = 0
s1
S
S1
S2
v r
v r
∫ B ⋅ ds1 = ∫ B ⋅ ds2
S1
S2
se la sezione S è costante allora
B1S1 = B2 S2
s2
n2
B1S = B2 S
B1 = B2
Φ( B) = BS = cost
Ovvero il flusso entrante attraverso una superficie s1 del circuito è uguale al
flusso uscente attraverso la superficie s2=s1 del circuito
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
34
III) equazione di Maxwell
Come è noto il campo elettrostatico è, in condizioni stazionarie, un campo
conservativo ovvero esiste una funzione potenziale V tale che:
r
E0 = −∇V
r r
V0 (a)- V0 (b)= ∫ E0 ⋅ dl
b
⇒
b
l
a
a
Se il campo è conservativo tale integrale non dipende dal cammino di
integrazione “l” ma soltanto dal punto iniziale “a” e dal punto finale “b”;
ovvero l’equazione rimane identicamente soddisfatta qualunque sia il
percorso “l” che porta dal punto “a” al punto “b” purchè “l” non passi per i
punti di singolarità di E0.
Il particolare se “a” coincide con “b”, qualunque sia la linea chiusa l di
integrazione si ha:
r r
V0 (a)- V0 (b)= ∫ E0 ⋅ dl = 0
b
l
a
b
a
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
35
III) equazione di Maxwell
Questa è una condizione necessaria e sufficiente affinché il campo E0 sia
conservativo e cioè che la circuitazione di E0 sia nulla.
Applicando il teorema di Stokes si ha:
r r
r r
0 = ∫ E0 ⋅ dl = ∫ (∇× E0 )ds
l
S
Dal momento che tale relazione vale per ogni linea chiusa l e per ogni
superficie S che abbia l come contorno, segue che deve essere nullo
l’integrando.
r
∇× E0 = 0
Questa esprime la III) equazione di Maxwell nel caso stazionario, ovvero
esprime in forma locale la conservatività del campo elettrostatico; si dice
anche che il campo elettrostatico è irrotazionale.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
36
III) equazione di Maxwell
Applicando tale osservazione al campo elettrico generato da una carica Q
puntiforme si ha:
r
1 Qv
E0 (r ) =
r
3
4πε0 r
con
v
r = rrˆ
allora integrandotra due punti
b
b
b
r r b 1 Qv r
1
1
Q
Q
Q
E
d
r
r
d
r
rdr
dr
⋅
=
⋅
=
=
=
∫a 0
∫a 4πε0 r 3
4πε0 ∫a r 3
4πε0 ∫a r 2
4πε0
⎡1 1⎤
⎢ − ⎥
⎣ ra rb ⎦
• Questo risultato mostra che il campo elettrico generato da una carica
puntiforme è un campo conservativo in quanto il suo integrale di linea fra due
posizioni non dipende dalla particolare traiettoria.
• Il potenziale elettrostatico in un punto (x,y,z) della curva di integrazione
generato dalla carica puntiforme Q è:
( x, y , x )
r r
V0(x,y,z) = ∫ E0 ⋅ dl + V0(a)
a
Davide Micheli
⎡N ⎤ ⎡ J ⎤
⎢⎣ C m⎥⎦ = ⎢⎣ C ⎥⎦ = [V ]
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
37
III) equazione di Maxwell
Il potenziale V0(x,y,z) corrisponde all’energia potenziale già introdotta per i
campi conservativi con la precisazione che ci si riferisca ad una carica unitaria
Dalla legge di Faraday Newmann segue per un circuito chiuso:
r
r v
r
r
dΦ ( B )
d r r
= − ∫ B ⋅ ds
f =−
risulta anche : f = ∫ E ⋅ dl = (per Stokes ) = ∫ (∇ × E ) ⋅ ds
dt
dt S
l
S
eguagliand o le due espression i :
⇓
r
r
d r r
− ∫ B ⋅ d s = ∫ (∇ × E ) ⋅ d s
dt S
S
⇒
r
r
r
dB r
−∫
⋅ d s = ∫ (∇ × E ) ⋅ d s
dt
S
S
eguagliand o gli itegrandi si ottienela III) equazione di Maxwell nel caso non stazionari o :
se il campo magnetico non è stazionari o allora è presente un campo elettrico non conservati vo
r
r
dB
III) ∇× E = −
dt
Davide Micheli
III) eq. Maxwell
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
38
IV) equazione di Maxwell
Una proprietà fondamentale di B riguarda la sua circuitazione: ovvero in
termini differenziali locali si dimostra che la circuitazione di B è in generale
diversa da zero: è detto Teorema della circuitazione di Ampere
r v
∫ B⋅ dl = nµ0I
l
l
L
• La circuitazione di B lungo una qualunque linea chiusa orientata L è pari alla
corrente I con la quale la linea chiusa si concatena moltiplicata per µ0
moltiplicata a sua volta per il numero di concatenazioni n.
• Se il campo B è generato da più di un solo circuito allora tenendo presente
che per le sue proprietà il campo B così come E è additivo, allora si ha:
r v
∫ B⋅ dl = µ0 ∑(Iini ) = µ0(1⋅ I1 −1⋅ I3 −2⋅ I2 +0⋅ I4)
l1
l3
l2
l
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
L
l4
39
IV) equazione di Maxwell
Le correnti vanno prese con il segno positivo o negativo a seconda che esse
vedano circolare intorno a se la linea orientata L in senso antiorario o in senso
orario. Poiché la corrente I è pari a:
r r
r
∑Ii = ∫ J ⋅ ds = Φ(J)
⇒
S
r v
r r
∫ B⋅ dl = µ0 ∑Ii = µ0 ∫ J ⋅ ds
l
S
ds
n
Dal teorema del rotore segue:
r v
r v
∫ B⋅ dl = ∫(∇×B)⋅ ds ⇒
l
S
r v
r v
∫ (∇×B)⋅ ds = µ0 ∫ J ⋅ ds
S
S
L
Poiché questa relazione deve valere qualunque sia la linea chiusa L e
qualunque sia la superficie aperta avente L come contorno, allora l’eguaglianza
degli integrali implica quella degli integrandi:
r
r
∇× B = µ0J
Questa è la Quarta equazione di Maxwell nel caso stazionario
la Quarta equazione di Maxwell nel caso stazionario mostra che ameno che
sia J=0, il campo B non è conservativo, e dunque non è possibile introdurre, in
analogia col potenziale elettrostatico, un potenziale scalare magnetostatico.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
40
IV) equazione di Maxwell
Per una proprietà matematica generale si ha che la divergenza di un rotore è
r r
r r
r
r
nulla:
∇ ⋅ ( A × B) = B ⋅ ∇ × A − A ⋅ ∇ × B
r
r⇓
r
∇ ⋅ (∇ × B) = B ⋅ (∇ × ∇) − ∇ ⋅ ∇ × B = 0
r ⇓
r
0 = ∇ ⋅ (∇ × B) = ∇ ⋅ (µ0 J )
⇓
r
∇⋅ J = 0
Questa è l’equazione di continuità nel caso stazionario:
(
)
(
(
)
)
Questa è l’equazione di continuità ne caso non stazionario:
r ∂ρ
∇⋅ J + = 0
∂t
La dimostrazione di questa equazione è riportata più avanti. Per ora la si applica
per determinare le correnti.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
41
IV) equazione di Maxwell
Il teorema della circuitazione di Ampere ovvero la sua espressione locale
rappresentata dalla quarta equazione di Maxwell può essere adattata al caso non
stazionario. Si parte dalla equazione di continuità delle correnti:
r ∂ρ
∇⋅ J + = 0
∂t
Sostituendo al posto della densità di carica ρ la sua espressione locale fornita
dalla I eq. Di Maxwell si ottiene:
r ρ
∇⋅ E =
ε
r
⇒ ρ = ε∇⋅ E
( )
r
v ∂ ∇⋅ E
=0
⇒ ∇⋅ J +ε
∂t
Invertendo l’ordine di derivazione come consentito dal teorema di Schwartz:
r
v
⎛ ∂E ⎞
∇⋅ J +ε∇⋅ ⎜⎜ ⎟⎟ = 0
⎝ ∂t ⎠
⇒
Davide Micheli
r
⎛ v ∂E ⎞
∇⋅ ⎜⎜ J +ε ⎟⎟ = 0
∂t ⎠
⎝
Densità di corrente di
spostamento
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
42
IV) equazione di Maxwell
Confrontando le equazioni nei casi stazionario e non stazionario si vede che la
divergenza di una certa quantità vettoriale è sempre nulla:
r
∇⋅ J = 0
r
⎛v
∂E ⎞
⎜
⎟=0
∇⋅⎜ J + ε
⎟
∂
t
⎝
⎠
• Si deduce che la quantità dentro parentesi è ancora una densità di corrente,
data dalla somma di due termini, il primo è la corrente di conduzione e il
secondo è chiamato corrente di spostamento è dovuta alla variazione nel
tempo del campo elettrico che è nulla nel caso stazionario.
• Partendo da questo ragionamento si può sostituire in termine comprensivo
della densità di corrente generalizzata nella quarta equazione di Maxwell già
vista, ottenendone la generalizzazione al caso non stazionario:
IV)
r
r
r
v
⎛ v ∂E ⎞
∂E
∇× B = µ0⎜⎜ J +ε ⎟⎟ = µ0J + µ0ε
∂t
∂t ⎠
⎝
Davide Micheli
IV eq Maxwell
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
43
IV) equazione di Maxwell
Integrando entrambi i membri di questa equazione su una superficie S
delimitata dalla linea chiusa L si ottiene il teorema della circuitazione di
Ampere nel caso non stazionario:
r
Teorema della
r r
v r
∂E r
∇ × B ⋅ ds = µ0 ∫ J ⋅ ds + µ0 ∫ ε
⋅ ds = µ0 I conduzione + µ0 I spostamento circuitazione di
∂t
S
S
Ampere
∫(
S
)
per il teoremadi Stokessi ottiene:
r r
∫ B ⋅ dL = µ0 Iconduzione + µ0 I spostamento
L
Dal teorema della divergenza segue il principio di Kirchoff per le correnti :
∫
S
v r
v
f ⋅ ds = ∫ (∇ ⋅ f )dτ
τ = volume definito dalla supericie S
τ
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
44
Legge di Hopkinson: circuiti elettrici e magnetici
So consideri un tubo di flusso per il campo di induzione magnetica B , e le due
r v
equazioni:
∫ B ⋅ dl = µNI
l
r
r r
Φ(B) = ∫ B ⋅ ds
n
S
S
Poiché B è parallelo a dl e a ds allora i rispettivi
prodotti scalari forniscono le seguenti:
dl
ds
B
r v r r
B⋅ dl = B⋅ n dl = Bdl
e
r
r r r r
⎡ Φ⎤
Φ(B) = ∫ B⋅ ds =∫ B⋅ n ds = B∫ ds = BS ⇒ ⎢B = ⎥
⎣ S⎦
S
S
S
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
45
Legge di Hopkinson: circuiti elettrici e magnetici
Sostituendo nel primo integrale si ottiene:
r v
1
Φ
⋅
=
=
=
dl
Φ
B
d
l
Bdl
∫l
∫l
∫l S
∫l S dl =µNI
⇓
NI = Φ ∫
l
1
dl
µS
ponendo :
F = NI
R=∫
si
ottinene :
l
1
dl
µS
= Forza magnetotri ce misurata
[Ampere spi re ]
= Riluttanza magnetica misurata
⎡ Ampere spi re ⎤
⎢
⎥
Weber
⎣
⎦
F = RΦ
detta legge di Hopkinson analoga alla
V = RI
detta legge di Ohm
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
46
Continuità della carica
Si consideri l’equazione di Maxwell:
r
r
r
ϑE
∇ ∧ B = µ J + µε
ϑt
Applicando l’operatore divergenza ad entrambi i membri si ottiene:
r
r
r
⎛
ϑE ⎞
⎟
∇ ⋅ ∇ ∧ B = ∇ ⋅ ⎜⎜ µ J + µε
ϑt ⎟⎠
⎝
r
r
⎛ ϑE ⎞
⎟
0 = µ∇ ⋅ J + µε∇ ⋅ ⎜⎜
⎟
⎝ ϑt ⎠
(
)
ma la divergenza di un rotore è nulla pertanto
L’operazione di divergenza è un’operazione di derivata nello spazio (x,y,z). Il
tempo è la quarta variabile indipendente, pertanto è possibile invertire l’ordine
di derivazione:
r
r
ϑ
0 = µ∇ ⋅ J + µε ∇ ⋅ E
ϑt
Davide Micheli
ma dalla
I) eq. Maxwell
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
r ρ
∇⋅E =
ε
47
Continuità della carica
dove ρ è la densità di carica misurata in C/m3
l’equazione di continuità della carica:
r
ϑρ 1
0 = µ∇ ⋅ J + µε
ϑt ε
⇒
sostituendo si ottiene
r ϑρ
∇⋅ J +
=0
ϑt
È importante perché completa il SECONDO PRINCIPIO DI KIRCHOFF: la somma
delle correnti entranti in un volume chiuso non è uguale a 0; lo è solo se non vi
è variazione temporale di carica in questo volume
I1
I2
Per comprendere il significato di tale
equazione, si consideri un volume τ
chiuso da una superficie S, corredato da
una serie di conduttori metallici in esso
entranti:
Davide Micheli
S
Q=0=costante ?
I4
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
I3
48
Continuità della carica
Calcolando l’integrale di volume della divergenza di J si ottiene (per il teorema
della divergenza) la somma delle correnti:
∫(
τ
)
r
r r
∇ ⋅ J dτ = ∫ J ⋅ ds =I
s
Se la corrente arrivasse esclusivamente attraverso i conduttori, integrando
ogni volta la densità di corrente nella sezione del conduttore risulterebbe che
l’integrale di volume della divergenza di J sarebbe la somma delle correnti
uscenti:
∫(
τ
)
r
r r
r r
r r
r r
r r
∇ ⋅ J dτ = ∫ J ⋅ ds = ∫ J ⋅ ds1 + ∫ J ⋅ ds2 + ∫ J ⋅ ds3 + ∫ J ⋅ ds4 =I1 + I 2 + I 3 + I 4 = I
S
S1
S2
S3
S4
a sua volta uguale a “meno” la derivata nel tempo della carica totale ( in quanto
l’integrale di volume della densità di carica restituisce la carica totale contenuta
all’interno del volume) e questo deriva direttamene dall’equazione di continuità:
∫(
τ
)
r
∂
∂Q 4
⎛ ∂ρ ⎞
= ∑ I i =I
∇ ⋅ J dτ = ∫ ⎜ − ⎟dτ = − ∫ ρ dτ = −
∂t τ
∂t i =1
∂t ⎠
τ ⎝
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
49
Continuità della carica
Si immagini una sfera dalla quale escano diversi conduttori:
Se si integra la relazione precedente su questo volume la corrente è zero, tranne
dove ci sono i conduttori.
Integrando la densità di corrente attraverso la sezione dei conduttori si
ottengono le varie correnti.
Domanda: all’interno del volume c’è una carica Q che è 0, o quantomeno
costante ?
Risposta: Non è affatto detto.
Se la carica contenuta in un certo volume è costante, non ci sono complicazioni.
Prima di applicare Kirchoff alle correnti, quindi, occorre ricordare che Maxwell
afferma che la somma delle correnti è uguale a “meno” la derivata nel tempo
della carica, e non afferma che è uguale a zero!
∂Q
I = ∑ Ii = −
∂t
i =1
4
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
50
Equazione delle onde elettromagnetiche
Si consideri un mezzo dielettrico illimitato, isotropo e omogeneo, e tale che il
dielettrico sia ovunque elettricamente neutro (assenza di cariche localizzate
ρ=0 ; se si tratta di un dielettrico perfetto (e dunque in particolare
perfettamente isolante, dotato cioè di resistenza elettrica infinita) sappiamo
che è parimenti j=0 (assenza di correnti macrosopiche).
Le equazioni di Maxwell nel dielettrico perfetto divengono quindi:
I) ∇• E =
ρ
=0
ε
III ) ∇ ∧ E = −
II) ∇ • B = 0
ϑB
ϑt
IV) ∇ ∧ B = µ j + µε
ϑE
ϑE
= µε
ϑt
ϑt
Applichiamo l’operatore rotore alla III di tali equazioni. Ricordando l’identità
matematica:
(
) (
)
r
r
r
2
∇× ∇× E = ∇ ∇⋅ E − ∇ E
Davide Micheli
r ρ
ma ∇ ⋅ E = = 0
ε
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
51
Equazione delle onde elettromagnetiche
si ricava l’equazione delle onde:
r
r
r
r
⎛ ∂B ⎞
∂
2
∇ × ∇ × E = −∇ E = ∇ × ⎜⎜ − ⎟⎟ = − ∇ × B
∂t
⎝ ∂t ⎠
⇓
r
r
2
r
∂ ⎛ ∂E ⎞
∂ E
⎟ = − µε 2
ovvero
− ∇ 2 E = − ⎜⎜ µε
⎟
∂t ⎝
∂t ⎠
∂t
(
)
(
)
r
r
∂E
ma ∇ × B = µε
∂t
r
2
r
∂ E
∇ 2 E − µε 2 = 0
∂t
Un equazione del tutto analoga vale per B, applicando il rotore alla quarta eq. e
confrontando con la derivata temporale della terza.
r
r
∂ B
2
∇ B − µε 2 = 0
∂t
2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
52
Equazione delle onde elettromagnetiche
• Prima di proseguire si ricordano alcune definizioni e nomenclature relative alle
onde.
• Una funzione f(x,t) rappresenta un’onda di ampiezza costante che si propaga
lungo l’asse x se in essa la dipendenza dalla coordinata x e dal tempo t
compare solo nella combinazione ε = (x⎯± vt) con v costante positiva.
• L’onda si dice progressiva o regressiva a seconda che compare il segno – o il
segno +.
f ( x, t ) = f ( x m vt )
Tale equazione rappresenta un onda infatti la f(x⎯+ vt) definisce un profilo; tale
profilo trasla senza cambiare forma lungo l’asse x con velocità ±v. infatti
consideriamo un certo valore ε1 = (x1⎯+ vt1), allora all’istante t2=(t1+∆t) , lo
stesso valore ε1 si presenta non più in x1 ma in x2= (x1+ ∆x) purchè ∆x sia legato
a ∆t dalla relazione:
x1 m vt1 = ( x1 + ∆x ) m v(t1 + ∆t ) = x1 m vt1 + ∆x m v∆t
∆x
= ±v
⇒
∆t
⇓
f ( x2 m vt2 ) = f [( x1 + ∆x ) m (vt1 + v∆t )] = f [x1 m vt1 + ∆x m v∆t ] =
= f [x1 m vt1 + (± v∆t m v∆t )] = f [x1 m vt1 + (0)] = f ( x2 m vt2 )
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
53
Equazione delle onde elettromagnetiche
f
f
∆x
t
ε= x⎯+ vt
t+ ∆t
x
• Nella maggior parte dei fenomeni fisici (ad esclusione di una corda vibrante)
la propagazione ondosa è un fenomeno tridimensionale.
• Si chiama allora fronte d’onda il luogo dei punti in cui, ad un fissato istante, la
variabile ε assume lo stesso valore.
• Un onda bidimensionale si dice rettilinea o circolare (ad esempio) se i suoi
fronti d’onda sono rettilinei o circolari, analogamente un onda tridimensionale
si dice piana se i suoi fronti d’onda sono superfici piane; si dice sferica se i
suoi fronti d’onda sono superfici sferiche; ecc.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
54
Equazione delle onde elettromagnetiche
Per esempio, se considerata come un onda nello spazio la:
f ( x, t ) = f ( x m vt )
Rappresenta un onda piana: l’argomento ε, essendo indipendente da y e z,
fissati x e t assume infatti lo stesso valore su tutto il piano perpendicolare
all’asse x passante per il valore di x considerato.
y
x
Fronte d’onda piano
z
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
55
Equazione delle onde elettromagnetiche
Se la f(ε) è una funzione periodica del suo argomento, l’onda è detta onda
periodica. In particolare sono periodiche le onde sinusoidali, cui per rendere
adimensionale l’argomento si da usualmente una delle seguenti espressioni
tra loro equivalenti:
⎤
⎡
⎥
⎢ 2π
⎡ 2π ⎛ x − vt ⎞ ⎤
⎡ 2π ⎛ x ⎞ ⎤
⎤
⎡ 2π
f ( x, t ) = A sin ⎢ ( x − vt ) + ϕ ⎥ = A sin ⎢ ( x − vt ) + ϕ ⎥ = A sin ⎢ v⎜
⎟ + ϕ ⎥ = A sin ⎢ ⎜ − t ⎟ + ϕ ⎥ =
⎦
⎣λ
⎥
⎢ v
⎣ vT ⎝ v ⎠ ⎦
⎣ T ⎝v ⎠ ⎦
⎥⎦
⎣⎢ f
⎡ ⎛
⎞ ⎤
⎜
⎟ ⎥
⎢
⎡ ⎛ x vt ⎞ ⎤
⎡ ⎛x t ⎞ ⎤
x
vt
⎡ 2π
⎤
f ( x, t ) = A sin ⎢ ( x − vt ) + ϕ ⎥ = A sin ⎢2π ⎜ − ⎟ + ϕ ⎥ = A sin ⎢2π ⎜ − ⎟ + ϕ ⎥ = A sin ⎢2π ⎜ − ⎟ + ϕ ⎥ =
⎢ ⎜λ v ⎟ ⎥
⎣λ
⎦
⎣ ⎝λ λ ⎠ ⎦
⎣ ⎝λ T ⎠ ⎦
⎜
⎟
⎢⎣ ⎝
f ⎠ ⎥⎦
⎡
⎤
⎢
⎥
2π
2π
⎡ 2π
⎤
⎡ 2π
⎤
f ( x, t ) = A sin ⎢ ( x − vt ) + ϕ ⎥ = A sin ⎢ x −
vt + ϕ ⎥ = A sin ⎢kx −
vt + ϕ ⎥ = A sin[kx − 2πft + ϕ ] = A sin[kx − ωt + ϕ ]
v
λ
λ
λ
⎣
⎦
⎣
⎦
⎢
⎥
⎢⎣
⎥⎦
f
dove
ϕ = fase iniziale dell'onda
ε = kx − ωt + ϕ = fase dell'onda
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
56
Equazione delle onde elettromagnetiche
Un onda periodica è tale sia nella variabile x che nella variabile t. Il periodo
temporale T e quello spaziale λ sono legati dalla relazione:
v=
λ
T
= λf = λ
ω ω
=
2π k
Per come è stata definita, la
velocità ovvero, la velocità di
un qualunque fronte d’onda,
non è altro che la velocità con
cui si muove la fase dell’onda.
dove :
ω = 2πf =
f = 1/ T
k=
2π
λ
2π
T
è la pulsazione
Tale velocità è appunto detta
velocità di fase
è la frequenza
è il numero d' onda
λ
è la lunghezza d' onda
∆x
= ±v
∆t
è la velocità di fase d' onda
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
57
Onde elettromagnetiche piane
L’equazione delle onde è una equazione differenziale alle derivate parziali;
come tale le sue soluzioni sono determinate a meno di funzioni arbitrarie, che
possono essere ricavate solo imponendo le condizioni al contorno e le
condizioni iniziali. La configurazione cui corrisponde l’espressione più
semplice per le soluzioni è una configurazione piana (esempio ortogonale
all’asse x). In questo caso (caso di onda piana) tutte le componenti dei campi E
e B sono indipendenti da y e da z:
Ad ogni istante, E e B hanno lo stesso valore in tutti i punti di ogni piano
ortogonale all’asse x.
y
r
r
∂ E
2
∇ E − µε 2 = 0
∂t
2
x
z
r
r
∂ B
2
∇ B − µε 2 = 0
∂t
2
Fronte d’onda piano
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
58
Onde elettromagnetiche piane
Fisicamente, questa condizione non si verifica mai esattamente nella pratica;
tuttavia ad essa ci si approssima in molti casi (approssimazione di onda piana)
in particolare quando si sia interessati ad una porzione di spazio piccola, molto
lontana dalla sorgente (approssimazione di sorgente puntiforme).
Dal momento che tutte le componenti dei campi E e B sono indipendenti da y e
da z tutte le derivate dei campi rispetto ad y e z sono nulle ed il laplaciano si
riduce alla sola derivata seconda rispetto ad x. Ciascuna delle sei componenti
del campo elettromagnetico E e B soddisfa la stessa equazione; del tipo
equazione di d’Alambert):
2
f
∂
∇ 2 f − µε 2 = 0
∂t
2
2
2
2
f
f
f
f
∂
∂
∂
∂
dove ∇ 2 f = 2 + 2 + 2 = 2
∂x
∂z
∂y
∂x
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
59
Onde elettromagnetiche piane
La soluzione generale di questa equazione è del tipo:
ϕ (x, t ) = f1 (x − vt ) + f 2 (x + vt )
con :
v=
1
µε
Dove f1 ef f2 sono due funzioni arbitrarie che ammettono derivata seconda
rispetto all’argomento ε = x±vt, cioè la soluzione generale è la somma di un
onda progressiva e di un onda regressiva propagantesi con velocità v lungo
l’asse x.
Se ci troviamo nel vuoto, la velocità v delle onde elettromagnetiche viene
indicata con c:
c=
1
µ0ε 0
Davide Micheli
≅ 2,998 ⋅108 m / s
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
60
Onde elettromagnetiche piane
In un dielettrico perfetto qualunque, avremo:
v=
1
µε
=
1
1
µ0ε 0
µrε r
Il rapporto:
n=
≅
c
µrε r
m/ s
c
v
fra la velocità della luce nel vuoto e la velocità della luce nel mezzo materiale
trasparente è detto indice di rifrazione di quel materiale; poiché in un
dielettrico perfetto la permeabilità magnetica relativa è µr=1 allora segue che:
1
c
n= =
v
µ0ε 0
1
1
µ0ε 0
µrε r
Davide Micheli
= µ r ε r = 1⋅ ε r = ε r
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
61
Onde elettromagnetiche piane
Ricaviamo ulteriori proprietà delle onde elettromagnetiche piane utilizzando le
equazioni di Maxwell cui devono soddisfare. Ricordiamo che tutte le
componenti dei campi sono indipendenti da y e z e dunque sono nulle le
rispettive derivate parziali rispetto a y e z :
I)
II )
III )
r
∇⋅E = 0
v
∇⋅B = 0
⇒
⇒
v
r
∂B
∇×E = −
∂t
∂E y
ˆi ⎛⎜ ∂ E z −
⎜ ∂y
∂z
⎝
⎞
⎟⎟ +
⎠
∂E x
∂E x ∂E y ∂E z
=0
=0 ⇒
+
+
∂x
∂y
∂z
∂x
∂B x ∂B y ∂B z
∂B x
+
+
=0 ⇒
=0
∂x
∂z
∂x
∂y
ˆj
iˆ
kˆ
∂B y
∂
∂
∂
∂B
ˆj − ∂B z kˆ
⇒
= − x iˆ −
∂x ∂y ∂z
∂t
∂t
∂t
Ex E y Ez
∂E
ˆj ⎛⎜ ∂ E x − ∂ E z ⎞⎟ + kˆ ⎛⎜ y − ∂ E x
⎜ ∂x
∂x ⎠
∂y
⎝ ∂z
⎝
[a ]
[b ]
⎞
∂B x ˆ ∂B y ˆ ∂B z ˆ
⎟⎟ = − ∂t i − ∂t j − ∂ t k
⎠
∂E
∂B y
ˆi (0 − 0 ) + ˆj ⎛⎜ 0 − ∂E z ⎞⎟ + kˆ ⎛⎜ y − 0 ⎞⎟ = − ∂B x iˆ −
ˆj − ∂B z kˆ
⎜ ∂x
⎟
∂x ⎠
∂t
∂t
∂t
⎝
⎝
⎠
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
62
Onde elettromagnetiche piane
Ricaviamo ulteriori proprietà delle onde elettromagnetiche piane utilizzando le
equazioni di Maxwell cui devono soddisfare. Ricordiamo che tutte le
componenti dei campi sono indipendenti da y e z e dunque sono nulle le
rispettive derivate parziali rispetto a y e z :
III )
IV )
v
r
∂B
∇× E = −
∂t
r
v
∂E
∇ × B = µε
∂t
⇒
∂Bx
⎧
=
0
⎪
∂t
⎪ ∂E
∂By
⎪
z
=−
⎨−
∂t
⎪ ∂x
⎪ ∂E y = − ∂Bz
⎪⎩ ∂x
∂t
∂Ex
⎧
=
0
⎪
∂t
⎪ ∂B
∂E y
⎪
⇒ ⎨ z = − µε
∂t
⎪ ∂x
⎪ ∂By = µε ∂Ez
⎪⎩ ∂x
∂t
Davide Micheli
[c]⎫⎪
⎪
[d]⎪⎬
⎪
[e]⎪⎪
⎭
[f ]⎫⎪
⎪
[g]⎪⎬
⎪
[h ]⎪⎪
⎭
Dalla [a] e [f] e dalla [b] e [c]
vediamo che Ex e Bx sono
costanti nel tempo ed uniformi
nello spazio. Esse pertanto non
contribuiscono al fenomeno
della propagazione del campo,
in altri termini le onde
elettromagnetiche
sono
puramente
trasversali,
la
componente
longitudinale
parallela alla direzione di
propagazione non contribuisce
alla propagazione stessa.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
63
Onde elettromagnetiche piane
Ricaviamo ulteriori proprietà delle onde elettromagnetiche piane utilizzando le
equazioni di Maxwell cui devono soddisfare. Ricordiamo che tutte le
componenti dei campi sono indipendenti da y e z e dunque sono nulle le
rispettive derivate parziali rispetto a y e z :
III )
IV )
v
r
∂B
∇× E = −
∂t
r
v
∂E
∇ × B = µε
∂t
⇒
∂Bx
⎧
⎪0 = ∂t
⎪ ∂E
∂By
⎪
z
=−
⎨−
∂t
⎪ ∂x
⎪ ∂E y = − ∂Bz
⎪⎩ ∂x
∂t
∂Ex
⎧
0
=
⎪
∂t
⎪ ∂B
∂E y
⎪ z
⇒ ⎨
= −µε
∂t
⎪ ∂x
⎪ ∂By = µε ∂Ez
⎪⎩ ∂x
∂t
Davide Micheli
[c]⎫⎪
⎪
[d]⎪⎬
⎪
[e]⎪⎪
⎭
[f ]⎫⎪
Dalla [d] e [e] e dalla [g] e [h]
vediamo che se l’onda ha una
componente Ey deve avere
anche una componente Bz (e
viceversa); e se ha una
componente Ez
deve avere
anche una componente By (e
viceversa)
⎪
[g]⎪⎬
⎪
[h ]⎪⎪
⎭
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
64
Onde elettromagnetiche piane: polarizzazione
Per la linearità delle equazioni di Maxwell, ogni combinazione lineare di
soluzioni è soluzione; e se si sovrappongono due soluzioni, una con E diretto
secondo l’asse y ed una con E diretto secondo l’asse z, si può ottenere
qualunque soluzione (con e E diretto in una direzione n qualunque del piano yz),
eventualmente variabile con x e t: n=n(x,t).
Non si ha dunque alcuna perdita di generalità se si considera un onda il cui
campo E sia orientato in direzione fissa ad esempio secondo l’asse y(Ez=0): una
tale onda si dice possedere polarizzazione piana o lineare ( secondo l‘asse y).
La più generale delle onde potrà essere ottenuta come sovrapposizione di un
onda polarizzata secondo y e di un onda polarizzata secondo z.
y
Ey
Ey x Bz
x
Bz
z
Fronte d’onda piano
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
65
Onde elettromagnetiche piane
Se Ez=0 le relazioni [d] e [h] divengono:
III )
IV )
v
r
∂B
∇× E = −
∂t
r
v
∂E
∇ × B = µε
∂t
⇒
∂Bx
⎧
=
0
⎪
∂t
⎪
∂By
⎪
=
−
0
⎨
∂t
⎪
⎪ ∂E y = − ∂Bz
⎪⎩ ∂x
∂t
∂Ex
⎧
=
0
⎪
∂t
⎪ ∂B
∂E y
⎪
⇒ ⎨ z = − µε
∂t
⎪ ∂x
⎪ ∂By = 0
⎪⎩ ∂x
Davide Micheli
[c]⎫⎪
⎪
[d]⎪⎬
⎪
[e]⎪⎪
⎭
[f ] ⎫⎪
⎪
[g]⎪⎬
⎪
[h ]⎪⎪
⎭
Dunque la componente By non
dipende ne da x ne da t: essa è
uniforme e costante, così come
già visto per Ex e Bx
Se il campo elettrico è diretto
secondo y, il campo magnetico è
diretto secondo z: in un onda
elettromagnetica,
campo
elettrico e magnetico sono fra
loro
ortogonali
(oltrechè
trasversali, cioè ortogonali alla
direzione di propagazione)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
66
Onde elettromagnetiche piane
Se Ez=0 dalle relazioni [e] e [g] si ha::
⎧ ∂Bx
⎪0 = ∂t
⎪
∂By
⎪
⎨0 = −
∂t
⎪
⎪ ∂Ey = − ∂Bz
⎪⎩ ∂x
∂t
III )
v
r
∂B
∇× E = −
∂t
IV )
∂Ex
⎧
=
0
⎪
∂t
r
⎪
v
∂Ey
∂E
⎪ ∂Bz
∇ × B = µε
⇒ ⎨
= −µε
∂t
∂t
⎪ ∂x
⎪ ∂By = 0
⎪⎩ ∂x
⇒
[c]⎫⎪
⎪
[d]⎪⎬
⎪
[e]⎪⎪
⎭
[f ] ⎫⎪
⎪
[g]⎪⎬
⎪
[h]⎪⎪
⎭
Le relazioni [e] e [g] contengono
una
rilevante
informazione
concernente le ampiezze relative
dei campi E e B. Ricordando
infatti che E e B sono vettori
diretti rispettivamente come y e
come
z
allora
ponendo
ε =(x⎯+ vt) si ha:
E y = E y ( x m vt ) = E y (ε )
Bz = Bz ( x m vt ) = Bz (ε )
L’equazione [e] diviene pertanto:
∂E y
∂E y ∂ε ∂E y
=
=
1
∂x
∂ε ∂x ∂ε
e
Davide Micheli
∂Bz
∂B ∂ε
∂B
=- z
= - z (m v )
∂t
∂ε ∂t
∂ε
⇒
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
∂E y
∂ε
= ±v
∂Bz
∂ε
67
Onde elettromagnetiche piane
La precedente è una equazione differenziale ordinaria del primo ordine, che
integrata per quadratura restituisce Ey= ±vBz+cost; dove la costante può
essere posta uguale a zero:
r r r
E = B×v
E
1
=v=
B
µε
Ricordando che E è diretto secondo y e B secondo z, allora il modulo del
rapporto Ey/Bz, rappresenta il rapporto dei moduli E e B di E e B. Tenuto conto
di ciò, e del risultato più sopra stabilito a proposito delle direzioni relative di E
e B e v, possiamo sintetizzare i risultati da noi ottenuti a proposito dei campi E
e B in un onda piana nelle relazioni:
Ey
Bz
= ±v
La seconda viene usualmente espressa in termini di E e di H anziché in termini di
E e B. Sostituendo in essa B=µH si ha:
E
µ
=
=Z
H
ε
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
68
Onde elettromagnetiche piane
La quantità Z ha le dimensioni di una impedenza e viene detta impedenza
caratteristica del materiale
µ
E
=
=Z
ε
H
Nel caso di onde elettromagnetiche nel vuoto l’impedenza caratteristica vale:
µ0
E
=
= Z 0 = 377
ε0
H
⎡ V/m ⎤ ⎡ V ⎤
⎢⎣ A/m ⎥⎦ = ⎢⎣ A ⎥⎦ = [Ω]
In un onda piana non solo il campo elettrico ed il campo magnetico devono
essere ortogonali, ma devono essere in fase ed inoltre il loro rapporto non
dipende dalla frequenza, ma dipende esclusivamente da µ e ε, cioè da come è
fatto il mezzo in cui l’onda si sta propagando.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
69
Unità logaritmiche
Applicazione ai segnali radioelettrici
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
70
Unità Logaritmiche per esprimere le potenze
L’unità adimensionale dB esprime il rapporto in maniera logaritmica tra due
grandezze, per esempio per i livelli di potenza P(W); di solito si sceglie un
riferimento:
⎛P⎞
dB = 10 Log ⎜⎜ ⎟⎟
⎝ P0 ⎠
Usando misure di
tensione è necessario tenere conto dell’impedenza
attraverso cui ciascuna tensione viene misurata:
⎛V2
⎜
⎛P⎞
10Log⎜⎜ ⎟⎟ = 10Log⎜⎜ R2
V0
⎝ P0 ⎠
⎜⎜
⎝ R0
⇓
⎞
⎟
⎟ = 20Log⎛⎜ V ⎞⎟ + 10Log⎛⎜ R ⎞⎟ =
⎜R ⎟
⎜V ⎟
⎟
0 ⎠
⎝
⎝ 0⎠
⎟⎟
⎠
⎛P⎞
⎛V ⎞
10Log⎜⎜ ⎟⎟ = 20Log⎜⎜ ⎟⎟
⎝ P0 ⎠
⎝ V0 ⎠
Davide Micheli
se :
R = R0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
71
Unità Logaritmiche dBm e dBµV
Considerando come grandezze di riferimento le seguenti:
P0 = 1 [mW ]
V0 = 1 [µV ]
⎛ P[W ] ⎞
P[dBmW ] = P[dBm ] = 10Log⎜⎜ −3
⎟⎟ = 10Log(P[W ]) + 10Log 103 =
⎝ 10 [W ] ⎠
( )
= 10Log(P[W ]) + 30Log(10) = 10Log(P[W ]) + 30
dove : 10Log(P[W ]) = P[dBW ]
⎛ V ⎞
P[dBµV ] = 20Log⎜⎜ −6 ⎟⎟ = 20Log(V ) + 20Log 106 =
⎝ 10 [V ] ⎠
( )
= 20Log(V ) + 120Log(10) = 20Log(V ) + 120
dove :
20Log(V ) = P[dBV ]
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
72
Unità Logaritmiche dBm e dBµV
Le relazioni reciproche sono :
P[dBm ] − 30 = 10Log(P[W ])
10
= 10 (
P [dBm ]−30
Log P [W ]10
P[W ] = 10
( P[dBm ]−30 )1 / 10
) = P[W ]10
= 10
P [dBm ]−30
10
= 10
P [dBm ]
−3
10
=
P [dBm ]
10
10
103
P[dBµV ] − 120 = 20Log(V )
10
[
]
P dBµV −120
= 10
Log (V )20
(P[dBµV ]−120)1 / 20
P[V ] = 10
[
= 10
Davide Micheli
]
P dBµV −120
20
[
= 10
P dBµV
20
[
P dBµV
]
10 20
−6
10 =
106
]
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
73
Unità Logaritmiche: passaggio da dBµV a dBm
V2
da : P =
R
⇒ V = PR
⎛ PR ⎞
⎛ V ⎞
1/ 2
P[dBµV ] = 20Log⎜ −6 ⎟ = 20Log⎜⎜ −6 ⎟⎟ = 20Log(PR) + 20Log 106
⎝ 10 ⎠
⎝ 10 ⎠
( )
= 10Log(PR) + 120 = 10Log(P[W ]) + 10Log(R ) + 120 =
⎛ P[W ]⋅10−3 ⎞
⎛ P[W ] ⎞
−3
⎟
(
)
(
)
= 10Log⎜⎜
+
+
=
10
120
10
+
10
+
120
+
10
(
10
)
Log
R
Log
Log
R
Log
⎜
⎟
−3
−3
⎟
⎝ 10 ⎠
⎝ 10
⎠
= P[dBm] + 10Log(R ) + 120 − 30
se
R = 50Ω
allora si ottiene:
P[dBµV ] = P[dBm] + 10Log(50) + 120 − 30 = P[dBm] + 17 + 120 − 30
⇓
P[dBµV ] = P[dBm] + 107
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
74
Unità Logaritmiche: passaggio da dBµV a dBµV/m
È necessario introdurre il fattore di antenna K pertanto considerando un onda
incidente su un antenna collegata ad un carico zL come in figura si ha:
Dipolo
Ei (µV/m)
zL(Ω)
VL(µV)
Carico
Ei
campo elettrico incidente
VL
tensione ai morsetti di
antenna chiusa su un carico
specifico
Per definizione l’Antenna Factor (AF) che si misura in [m-1] è dato da:
AF =
Ei
VL
[m ]
-1
⇒
(
−1
AF dBm
⇓
(
)
⎛ Ei [µV / m] ⎞
⎟ = Ei [dBµV / m] − VL [dBµV ]
= 20Log⎜⎜
⎟
[
]
µ
V
V
L
⎝
⎠
Ei [dBµV / m] = VL [dBµV ] + AF dBm−1
Davide Micheli
)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
75
Unità Logaritmiche: passaggio da dBm a dBµV/m
Il passaggio è immediato utilizzando le relazioni già viste:
(
Ei [dBµV / m] = P[dBm] + 107 + AF dBm−1
10
10
Ei [dBµV / m ]
⎛⎡ V ⎤⎞
⎜ ⎢ −6 ⎥ ⎟
Log ⎜ ⎣ 10 ⎦ ⎟
⎜ m ⎟
⎜
⎟
⎝
⎠
= 10
⎛⎡ V ⎤⎞
⎜ ⎢ −6 ⎥ ⎟
20 Log ⎜ ⎣ 10 ⎦ ⎟
⎜ m ⎟
⎟
⎜
⎠
⎝
= 10
)
(
P [dBm]+107+ AF dBm−1
)
20
20
⎛⎡ V ⎤⎞
⎜ ⎢ −6 ⎥ ⎟
10 ⎦ ⎟
⎣
P [dBm]+107+ AF (dBm−1 )
⎜
=
= 10
⎜ m ⎟
⎜
⎟
⎝
⎠
⎡ V ⎤
P [dBm]+107+ AF (dBm−1 )
⎢⎣10−6 ⎥⎦
−1 1 / 20
= 10 P[dBm]+107+ AF (dBm )
= 10
m
20
(
)
Ei [V / m] = 10−6 ⋅10
Davide Micheli
(
P [dBm]+107+ AF dBm−1
20
)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
76
Unità Logaritmiche: passaggio da dBm a dBµV/m
Alla relazione precedente si arriva anche mediante i seguenti passaggi:
sia δ è la densità di potenza generata dall’antenna trasmittente in un punto a
distanza d
δ=
Pt × Gt
4×π × d 2
In condizioni di campo lontano cioè per un onda piana tale densità di potenza
è anche uguale a:
δ=
E2
η
•η è l’impedenza caratteristica del vuoto,
•λ è la lunghezza d’onda del segnale utile,
•Pr è la potenza ricevuta dal ricevitore nel punto considerato (W),
•Gr è il guadagno del ricevitore,
•freq è la frequenza in Hz
moltiplicando la densità di potenza per l’area efficace dell’antenna ricevente
si ottiene si ottiene la potenza ricevuta:
Pr = δ × Aeff .
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
77
Unità Logaritmiche: passaggio da dBm a dBµV/m
si sa che l’area efficace di un’antenna è legata al suo guadagno attraverso la
seguente relazione:
Aeff .
λ2
=
× Gr
4 ×π
sostituendo tale valore nell’espressione della potenza ricevuta si ha
E2
λ2
λ2
Pr = δ ×
× Gr =
×
× Gr
4×π
η 4×π
invertendo la relazione si ottiene:
η × Pr× 4 × π
Er =
λ 2 × Gr
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
78
Unità Logaritmiche: passaggio da dBm a dBµV/m
Dal momento che esiste una relazione che lega l’Antenna Factor al guadagno
si può scrivere:
AF =
η 4π
λ2 RradiazioneGRX
⇒
GRX =
sostituendo GRX nell' espressione del
E=
η ⋅ Pr⋅ 4π
η ⋅ Pr⋅ 4 ⋅ π
=
=
2
η 4π
λ ⋅ Gr
λ2 ⋅ 2
λ Rradiazione AF 2
= AF Pr⋅ Rradiazione
η 4π
λ2 Rradiazione AF 2
campo elettrico si ha :
Pr
1
=
Rradiazione AF 2
⎡ W ⋅V / A ⎤ ⎡ V ⋅ A ⋅V / A ⎤
miurato in ⎢
⎥=⎢
⎥ = [V / m]
m
m
⎣
⎦ ⎣
⎦
⎡V / 10−6 ⎤
⎡ µV ⎤ AF Pr⋅ Rradiazione
E⎢
E
=
=
⎥
⎢
⎥
10−6
⎣ m ⎦
⎣ m ⎦
⎧ ⎡V / 10−6 ⎤ ⎫
AF Pr⋅ Rradiazione
=
Log
20 Log ⎨ E ⎢
20
⎥⎬
−6
10
m
⎣
⎦
⎩
⎭
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
79
Unità Logaritmiche: passaggio da dBm a dBµV/m
E[dBµV / m] = 20Log( AF ) + 10Log(Pr[W ]) + 10Log( Rradiazione) + 20Log106 =
10−3
= 20Log( AF ) + 10Log(Pr[W ] ⋅ −3 ) + 10Log( Rradiazione) + 120 =
10
= 20Log( AF ) + P[dBm] + 10Log(10−3 ) + 10Log( Rradiazione) + 120 =
= 20Log( AF ) + P[dBm] − 30 + 10Log(50) + 120 =
= 20Log( AF ) + P[dBm] + 107
[
]
= AF dBm−1 + P[dBm] + 107
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
80
Tratta radio
Una trasmissione radio può essere schematizzata mediante i seguenti blocchi
fondamentali:
TRATTA RADIO
G1
Mu
Mo
AF
AL1
Tx
G2
AL2
Rx
De
Mu
A0
A
AT
Mu:
Mo:
T:
R:
De:
multiplex
modulatore RF
trasmettitore
ricevitore
demodulatore
AT: attenuazione complessiva di tratta hertziana
A: attenuazione di tratta
A0: attenuazione fondamentale di trasmissione
AL: attenuazione delle connessioni di antenna
AF: attenuazione aggiuntiva di fading
G1,2: guadagno di antenna
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
81
Tratta radio: trasmissione in spazio libero
Per la parte radio, l’attenuazione complessiva di tratta hertziana si trova
mediante la seguente:
AT = A0 −(G1 −G2 ) + AL1 + AL2 + AF
(dB)
La parte di tratta che comprende antenna trasmittente ed antenna ricevente
caratterizza la trasmissione nello spazio che ipotizziamo essere “spazio libero”
ricevitore
trasmettitore
WTA
Tx(A)
r
WRB
)
(B
x
R
ΘB,ФB
ΘA,ФA
WTA:
potenza trasmessa in ingresso all’antenna A
WTB:
potenza ricevuta in uscita dall’antenna B
G(Θ,Ф): guadango delle antenne rispetto alla direzione di massima radiazione
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
82
Tratta radio: trasmissione in spazio libero
Su suppongono soddisfatte le seguenti ipotesi:
–
–
–
Campo lontano (cioè distanza r > 2d2/λ con d=dimensione maggiore lineare
dell’antenna)
Adattamento dei carichi ( in quanto si vuole il max trasferimento di potenza
senza effetti di potenza riflessa)
Adattamento di polarizzazione (per evitare perdite di potenza dovute a
polarizzazione diversa delle tra trasmissione e ricezione)
PB =
[
WTA
G A(ΘA ,ΦA )
2
4π r
WRB = PB ⋅ Aeff B (Θ
]
densità di potenza W/m 2 ricevuta a distanza " r" da A
potenza [W ] ai morsetti dalla antenna B
B ,ΦB )
dalla relazione che lega area efficace al guadagno di antenna si ha :
Aeff B (Θ
B ,ΦB
)
=
GB (ΘB ,ΦB )
4π
λ2
di conseguenza la potenza ricevuta ai morsetti dell' antenna B è :
WRB = PB ⋅
GB (ΘB ,ΦB )
4π
GB (ΘB ,ΦB ) 2
WTA
GA
λ
λ =
⋅
4π r 2 (ΘA,ΦA )
4π
2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
83
Tratta radio: attenuazione fondamentale di tratta
Pertanto si ottiene l’equazione di FRIIS:
2
WRB ⎛ λ ⎞
⎟⎟ GA(ΘA,ΦA )GB(ΘB,ΦB )
= ⎜⎜
WTA ⎝ 4π r ⎠
l’attenuazione fondamentale di tratta A0 di spazio libero è:
2
W ⎛ 4π rf ⎞ 1
A0 = TA = ⎜
⎟
WRB ⎝ c ⎠ GAGB
2
WTA ⎛ rc⎞
1
⎜
⎟
A0 =
=
WRB ⎜⎝ f ⎟⎠ Aeff A Aeff B
per antenneadapertural'areaeffettivaè
Aeff = η⋅ Ageometrica 0.5≤ η ≤ 0.75
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
84
Tratta radio: attenuazione fondamentale di tratta
Esprimendo l’equazione di Friis in decibel si ottiene:
⎛ λ ⎞
⎟⎟ + G A(Θ A ,Φ A ) (dB ) + GB (ΘB ,ΦB ) ( dB ) =
∆W ( dB ) = WRB ( dBm) − WTA (dBm) = 2 ⋅10 Log ⎜⎜
⎝ 4π r ⎠
⎛c⎞
= 2 ⋅10 Log ⎜⎜ ⎟⎟ − 2 ⋅10 Log (4π r ) + G A(ΘA ,Φ A ) ( dB ) + GB (ΘB ,ΦB ) (dB ) =
⎝f ⎠
= 20 Log (c ) − 20 Log ( f ) − 20 Log (4π ) + 20 Log (r ) + G A(Θ A ,Φ A ) ( dB ) + GB (ΘB ,ΦB ) (dB ) =
≅ 147,6 − 20 Log ( f ) + 20 Log (r ) + G A(Θ A ,Φ A ) ( dB ) + GB (ΘB ,ΦB ) (dB )
con :
r ≡ [m]
f ≡ [Hz ]
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
85
Tratta radio: attenuazione fondamentale di tratta
In condizioni reali all’attenuazione fondamentale di tratta A0 va aggiunta
l’attenuazione dovuta a fading (evanescenza) AF :
A = A0 + AF (dB)
Davide Micheli
riflessione
⎫
⎧
⎪
⎪
rifrazione
⎪
⎪
con : AF ⎨
difrazioneda ostacoli⎬
⎪
⎪ assorbimento
⎪ depolarizzazione ⎪
⎭
⎩
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
86
Ionosfera
Note sulla propagazione dei segnali radio
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
87
ionosfera
La ionosfera è uno strato (con caratteristiche dispersive per i segnali radio)
dell’atmosfera localizzato nella regione compresa tra 70Km e 1000 Km sopra la superficie
terrestre. Tale strato è così chiamato a causa dell’elevato numero di elettroni liberi e di
molecole ionizzate (cariche positivamente) formatesi a causa della radiazione proveniente
dal sole; tali particelle finiscono per ricombinarsi, con velocità di ricombinazione tanto
maggiore quanto più è denso il gas ionizzato. Il risultato è all’equilibrio, la presenza di un
certo numero di elettroni liberi e ioni.
All’aumentare della densità dell’atmosfera, penetrando quest’ultima a partire dalle quote
più elevate, la densità di ionizzazione N (numero di elettroni liberi per metro cubo)
aumenta fino a raggiungere un massimo per poi diminuire, sia per la diminuzione
dell’intensità delle radiazioni dovuta all’assorbimento nell’attraversare l’atmosfera, sia per
l’aumento della velocità di ricombinazione provocato dalla maggiore densità atmosferica.
La regione in cui il valore di N è apprezzabile è detta appunto ionosfera.
La densità di ionizzazione N in funzione della quota non presenta un solo massimo ma
più massimi relativi in corrispondenza dei quali si dice esistere uno strato ionosferico
Sia la quota che i valori dei massimi di N, come il loro numero, dipendono da vari fattori,
come la latitudine, l’ora del giorno, la stagione, il ciclo solare (con periodo di 11 anni).
Si può comunque stabilire l’esistenza durante il giorno di almeno quattro strati: strato
D(h=80 Km), strato E (h=110 Km), strato F1 (h=220 Km), strato F2(h=300 Km)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
88
Propagazione ionosferica
Si assumano le seguenti ipotesi:
Plasma:
Particelle negative:
Particelle positive:
Particelle neutre:
è costituito da un insieme di particelle cariche e
neutre; cariche + e cariche – ;
elettroni prodotti per ionizzazione dalla radiazione
ultravioletta , dai raggi X del sole e dai raggi cosmici
atomi ionizzati
atomi non ionizzati
La ionosfera è caratterizzata dalla densità N di elettroni liberi in funzione
dell’altezza sul livello del mare. Viene studiata per strati (C,D,E,F1,F2):
•Quota elevata: la radiazione ionizzante è elevata, il gas è molto rarefatto (il
valore di N è basso)
•Quota intermedia: vi è il migliore rapporto radiazione pressione atmosferica
(il valore di N è massimo)
•Quota bassa: radiazione minima ( N diminuisce)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
89
Propagazione di un onda E.M. nel plasma
Si assume un modello FLUIDODINAMICO: il plasma non più visto come un
insieme discreto di particelle, ma un continuo di particelle caratterizzato da
grandezze medie (N: numero di particelle per unità di volume)
Ipotesi:
1. Plasma freddo: cioè si trascurano gli effetti della pressione;
2. Assenza di attrito: non vi sono perdite dovute a collisioni, il tal caso la
costante dielettrica ε è reale, altrimenti dovremmo considerare un
coefficiente che tiene conto del numero di collisioni per unità di volume e per
unità di tempo e la costante dielettrica ε sarebbe complessa com ein un
mezzo con perdite.
3. Forze trascurabili: gravità, in quanto le forze di tipo elettrico sulle cariche
stesse dovuta alla presenza dell’onda E.M nel plasma è sicuramente molto
più grande rispetto alla forza di gravità che agisce sulla carica stessa. Inoltre
si trascura la mutua attrazione tra le cariche, nel senso che si suppongono
sufficientemente lontane da trascurare questo tipo di forza columbiana.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
90
Propagazione di un onda E.M. nel plasma
1. Solo gli elettroni si muovono: cioè gli ioni positivi molto più pesanti non si
muovono sotto l’effetto del campo E.M. infatti il rapporto tra massa di un
protone e di un elettrone è 1836. Una molecola essendo costituita da tanti
protoni e neutroni è sicuramente più pesante rispetto all’elettrone stesso
ed allora l’accellerazione che subisce un elettrone sarà ordini di grandezza
più elevata rispetto a quella subita dalla molecola stessa, tale da
considerare praticamente ferme le molecole rispetto all’elettrone stesso.
mprotone 1.67⋅10−27 Kg
=
=1836
−31
melettrone 9.1⋅10 Kg
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
91
Caratterizzazione del plasma
Si considerino le seguenti:
• N
cariche per unità di volume
• q
carica della particella
velocità della particella
• v
• m
massa della particella
• Nq
densità di carica
• j=NqV
densità di corrente
[C]
[m/s]
[Kg]
[C/m3]
[A/m2] : elettroni messi in
movimento dalla presenza delle onde ettromagnetiche e pertanto il
fenomeno è quantificabile tramite una densità di corrente.
•
Nm
densità di massa delle particelle [Kg/m3]
Consideriamo la terza e quarta
v equazione di Maxwell:
v
∂H
III ) ∇ × E = − µ 0
∂t
r
r
r
v
∂E
∂E
∇ × H = j + ε0
= Nq V + ε 0
∂t
∂t
IV )
Consideriamo la legge di Newton cioè forza uguale massa per accelerazione:
(
)
r
r
r v
v d NmV
F=
= Nq E + µ0V × H → densità di
dt
(
Davide Micheli
)
forza di Lorenz
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
92
Caratterizzazione del plasma
Consideriamo l’equazione di continuità della carica che non è utilizzata ma è
riportata per completezza:
(
)
r ∂ρ
r ∂Nq
= ∇ ⋅ NqV +
∇⋅ J +
=0
∂t
∂t
Sono equazioni non lineari in N,V,H !!!
Nel senso che vi sono prodotti di variabili dipendenti, ad esempio H è
moltiplicato per la velocità che a sua volta dipende dal cmpo e.m. indotto
dall’onda esterna.
per risolvere tali equazioni si può ricorrere ad una linearizzazione facendo
l’ipotesi di piccoli segnali ovvero ad una situazione di equilibrio con piccole
variazioni dovute all’interazione del plasma con il campo elettromagnetico
E.M.
Sostanzialmente il criterio di linearizzazione si basa su uno sviluppo in serie di
queste grandezze:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
93
Caratterizzazione del plasma
N0
∆N
è la densità media di particelle in assenza di campo elettromangetico
è la perturbazione dovuta alla presenza del campo elettromagnetico
Lo stesso per le altre grandezze:
N → N 0 + ∆N
r
r
r
V → V0 + ∆ V
v
v
v
H → H 0 + ∆H
con : N 0 = densità media delle particelle ;
con : V0 = eventuale velocità impressa
da un movimento iniziale delle cariche;
v
con : H 0 = campo magnetico statico impresso
( campo magnetico terrestre );
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
94
Caratterizzazione del plasma
Segue che sostituendo i termini alle variazioni si possono semplificare in
quanto sono piccoli rispetto agli altri; supponiamo inoltre che siamo in uno
stato di quiete cioè che non ci sia velocità di dirift delle particelle cioè V0=0 e
che H0 sia il campo magnetico terrestre costante:
r
r
r
r
r
r
r
r
NV ≅ ( N 0 + ∆N ) V0 + ∆V = N 0V0 + N 0 ∆V + ∆N V0 + ∆N ∆V ≅ N 0 ∆V
v
v
v
v
N E ≅ N 0 E + ∆N E ≅ N 0 E
r v
r
r
r
r
v
v
NV × H = N 0rV0 + N 0 ∆V + ∆
r N Vv0 + ∆N ∆rV ×v H 0 + ∆H r = v
v
N 0Vr0 × H 0 + N 0 ∆Vr × H 0 + ∆N Vr0 × H 0 + ∆N∆V r× H 0 +
v
v
v
v
N 0V0 r× ∆H + N 0 ∆V × ∆H + ∆NV0 × ∆H + ∆N∆V × ∆H
v
≅ N 0 ∆V × H 0
con
v
N 0 , H 0 costanti in tutto lo spazio
r
V0 = 0
r
∆N , ∆V piccole variazioni
(
)
(
)(
Davide Micheli
)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
95
Caratterizzazione del plasma
Inoltre dall’ipotesi di linearizzazione risulta che la variazione di V funzione
dello spazio e del tempo si riduce ad una funzione solo del tempo:
v r
V = V ( x, y, z, t )
v ⇓v
v
v
v
v
dV ∂V ∂V
∂V
∂V
∂V
=
+
Vx +
Vy +
Vz ≅
∂y
∂z
∂t
dt
∂t ∂x
Trascurabile per linearizzazione
Alla luce della linearizzazione le equazioni dell’interazione Campo-Plasma
sono:
r
r
r
v
r
r
v
v
∂H
∂E
∂E
∂E
∇× H = j + ε0
= NqV + ε 0
= N 0 q∆V + ε 0
III ) ∇ × E = − µ0
IV )
∂t
∂t
∂t
∂t
r
r
r
r
v d NmV
d ( N 0 + ∆N )m V0 + ∆V
N m ⋅ d ∆V
F=
=
= 0
=
dt
dt
dt
r
r v
r
r v
r
r v
= Nq E + µ0V × H = N 0 q E + µ0 ∆V × H 0 = N 0 qE + qN 0 µ0 ∆V × H 0
(
) (
(
(
)
(
Davide Micheli
))
( )
)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
96
Caratterizzazione del plasma
Rapportandoci ai fasori per un onda sinusoidale, ovvero ricordando che :
d jωt
e = jω ⋅ e jωt
dt
Allora le equazioni dell’interazione Campo-Plasma sono:
v
v
v
∂H
III ) ∇ × E = − µ 0
= − jωµ0 H
∂t
r
r
r
r
v
∂E
IV ) ∇ × H = N 0 q∆V + ε 0
= N 0 q∆V + jωε 0 E
∂t
Legge di Newton )
r
r
r v
jω m∆V = qE + qµ 0 ∆V × H 0
Dalla eq di Newton si ricava ∆V che sostituito nelle altre equazioni dei rotori
permette di ricavare E e H.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
97
Caratterizzazione del plasma
Ipotesi :
r
r
B B
H 0 = 0 = 0 zˆ
µ0
µ0
Cioè il campo magnetico terrestre è costante ed è diretto lungo l’asse z;
segue che:
Legge di Newton )
r
r
r v
r
r
qE = jω m∆V − qµ0 ∆V × H 0 = jω m∆V + qB0 zˆ × ∆V
Annotazione:
⎡ xˆ
yˆ
zˆ ⎤
⎡0 −1 0⎤ ⎡∆Vx ⎤
r ⎢
⎥
zˆ ×∆V = ⎢ 0
0
1 ⎥ = xˆ(− ∆Vy ) + yˆ(∆Vx ) = [xˆ yˆ zˆ]⋅ ⎢⎢1 0 0⎥⎥ ⋅ ⎢⎢∆Vy ⎥⎥
⎢∆Vx ∆Vy ∆Vz ⎥
⎢⎣0 0 0⎥⎦ ⎢⎣∆Vz ⎥⎦
⎣
⎦
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
98
Caratterizzazione del plasma
Segue che la legge di Newton può essere riscritta come:
⎡1 0 0⎤ ⎡ ∆Vx ⎤
⎡ Ex ⎤
q ⎢⎢ E y ⎥⎥ = jω m ⎢⎢0 1 0⎥⎥ ⎢⎢∆V y ⎥⎥ + qB0 [xˆ
⎢⎣0 0 1⎥⎦ ⎢⎣ ∆Vz ⎥⎦
⎢⎣ E z ⎥⎦
yˆ
⎡0 − 1 0⎤ ⎡ ∆Vx ⎤
zˆ ]⋅ ⎢⎢1 0 0⎥⎥ ⋅ ⎢⎢∆V y ⎥⎥
⎢⎣0 0 0⎥⎦ ⎢⎣ ∆Vz ⎥⎦
⎧
⎡0 −1 0⎤⎫ ⎡∆Vx ⎤
⎡1 0 0⎤
⎪⎢ ⎥
⎪
⎥
⎢
⎥
⎢
⎥
⎢
ˆ
ˆ
ˆ
[
]
q⎢Ey ⎥ = ⎨ jω m⎢0 1 0⎥ + qB0 x y z ⋅ ⎢1 0 0⎥⎬⋅ ⎢∆Vy ⎥ =
⎢⎣0 0 0⎥⎦⎪⎭ ⎢⎣∆Vz ⎥⎦
⎢⎣0 0 1⎥⎦
⎢⎣Ez ⎥⎦ ⎪⎩
Ovvero:⎡Ex ⎤
0 ⎤ ⎡ 0 − qB0 0⎤⎫ ⎡∆Vx ⎤
⎡Ex ⎤ ⎧⎡ jω m 0
⎪⎢
⎪⎢ ⎥
⎢
⎥
⎥
⎢
⎥
q⎢Ey ⎥ = ⎨⎢ 0 jω m 0 ⎥ + ⎢qB0
0 0⎥⎬⋅ ⎢∆Vy ⎥ =
⎢⎣Ez ⎥⎦ ⎪⎩⎢⎣ 0
0 jω m⎥⎦ ⎢⎣ 0
0 0⎥⎦⎪⎭ ⎢⎣∆Vz ⎥⎦
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
99
Caratterizzazione del plasma
Segue che la legge di Newton può essere riscritta come:
⎡ Ex ⎤ ⎡ jω m − qB0
q ⎢⎢ E y ⎥⎥ = ⎢⎢ qB0
jω m
⎢⎣ Ez ⎥⎦ ⎢⎣ 0
0
0 ⎤ ⎡∆Vx ⎤ ⎡∆Vx ⎤ ⎡ jω m − qB0
0 ⎥⎥ ⋅ ⎢⎢∆Vy ⎥⎥ ⇒ ⎢⎢∆Vy ⎥⎥ = ⎢⎢ qB0
jω m
jω m⎥⎦ ⎢⎣ ∆Vz ⎥⎦ ⎢⎣ ∆Vz ⎥⎦ ⎢⎣ 0
0
−1
0 ⎤ ⎡ Ex ⎤
0 ⎥⎥ q ⎢⎢ E y ⎥⎥
jω m⎥⎦ ⎢⎣ Ez ⎥⎦
r
v
−1
∆V = q[A] E
Ovvero:
Annotazione:
⎡a
⎢b
⎢
⎢⎣ 0
⎡a
⎢b
⎢
⎢⎣ 0
−b
a
0
−b
a
0
0⎤
0 ⎥⎥
a ⎥⎦
−1
⎡ a2
1
⎢
= 3
⋅
− ab
2 ⎢
a + ab
⎢ 0
⎣
⎡
1
−1
⎢
0⎤
⎢ b
1
⎥
⋅ ⎢−
0⎥ =
2
⎛ b ⎞ ⎢ a
a ⎜⎜1 + 2 ⎟⎟ ⎢
a ⎥⎦
⎝ a ⎠ ⎢ 0
⎣
−b
a2
0
−
⎡ a2
⎤
1
⎢
⎥
⋅
− ab
0 ⎥=
⎢
2
⎛ b ⎞
a 2 + b 2 ⎥⎦ a 3 ⎜⎜1 + 2 ⎟⎟ ⎢⎣ 0
⎝ a ⎠
⎤
0 ⎥
⎥
0 ⎥
con : a = jωm
⎥
2
b ⎥
1+ 2 ⎥
a ⎦
0
b
a
1
0
Davide Micheli
−b
a2
0
⎤
⎥
0 ⎥
a 2 + b 2 ⎥⎦
0
b = qB0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
ω
b qB0
=
=−j c
ω
a jω m
100
Caratterizzazione del plasma
qB0
ωc =
m
La quantità :
è la pulsazione di ciclotrone
Alla luce delle annotazioni fatte il vettore velocità diviene:
r
v
−1
∆V = q[A] E
⎡∆Vx ⎤
⎡ jω m − qB0
⎢∆V ⎥ = q ⎢ qB
⎢ y⎥
⎢ 0 jω m
⎢⎣∆Vz ⎥⎦
⎢⎣ 0
0
⎡
⎢ 1
−1
⎢
0 ⎤ ⎡Ex ⎤
⎢ ωc
1
⎥
⎢
⎥
j
0 ⎥ ⎢ Ey ⎥ = q
2 ⎢
⎛ ⎛ ωc ⎞ ⎞ ⎢ ω
⎥
⎢
⎥
jω m⎦ ⎣ Ez ⎦
jω m⎜1− ⎜ ⎟ ⎟ ⎢
⎜ ⎝ω⎠ ⎟
⎝
⎠⎢ 0
⎣
Davide Micheli
−j
ωc
ω
1
0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
⎤
⎥
0
⎥ ⎡ Ex ⎤
⎥ ⎢ ⎥
0
⎥ ⋅ ⎢ Ey ⎥
⎥ ⎢E ⎥
2
⎛ ⎛ ωc ⎞ ⎞⎥ ⎣ z ⎦
⎜1− ⎜ ⎟ ⎟
⎜ ⎝ ω ⎠ ⎟⎥
⎝
⎠⎦
101
Caratterizzazione del plasma
Poiché dalle eq di Maxwell si ha:
r
r
v
IV ) ∇ × H = N 0 q∆V + jωε 0 E
Allora sostituendo il termine trovato per la velocità si ottiene:
⎤
⎡
⎥
⎢ 1 − j ωc
0
⎥
⎢
ω
r
v
⎥ r
⎢ ωc
N0q2
IV) ∇× H = jωε0E − j
j
1
0
⎥⋅ E
2 ⎢
⎛ ⎛ ωc ⎞ ⎞ ⎢ ω
⎥
2
ω m⎜1−⎜ ⎟ ⎟ ⎢
⎛ ⎛ ωc ⎞ ⎞⎥
⎜ ⎝ω⎠ ⎟
⎜1−⎜ ⎟ ⎟
0
⎠⎢ 0
⎝
⎜ ⎝ ω ⎠ ⎟⎥
⎝
⎠⎦
⎣
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
102
Caratterizzazione del plasma
Allora sostituendo il termine trovato per la velocità si ottiene:
⎡
⎢ 1
N0q 2
⎢
⎡1 0 0⎤
2
r
v
ω mε 0 ⎢ ωc
IV ) ∇ × H = jωε 0 ⎢⎢0 1 0⎥⎥ E − jωε 0
⎢j
⎛ ⎛ ωc ⎞ 2 ⎞ ⎢ ω
⎜1 − ⎜ ⎟ ⎟
⎢⎣0 0 1⎥⎦
⎜ ⎝ ω ⎠ ⎟⎢
⎝
⎠⎢ 0
⎣
⎡
2
N
q
0
⎢
ω 2 mε 0
⎢
⎢ 1− ⎛
2
⎞
ω
⎞
⎛
⎢
⎜1 − ⎜ c ⎟ ⎟
⎜ ⎝ω⎠ ⎟
⎢
⎝
⎠
⎢
2
N0q
⎢
⎢
ω 2 mε 0 ωc
= jωε 0 ⎢− j
2
⎢ ⎛⎜ ⎛ ωc ⎞ ⎞⎟ ω
⎢ ⎜1 − ⎜⎝ ω ⎟⎠ ⎟
⎠
⎢ ⎝
⎢
⎢
⎢
0
⎢
⎢
⎣⎢
Davide Micheli
j
N0q 2
ω 2 mε 0
ωc
⎛ ⎛ ωc ⎞ 2 ⎞ ω
⎜1 − ⎜ ⎟ ⎟
⎜ ⎝ω⎠ ⎟
⎝
⎠
1−
N0q 2
ω 2 mε 0
⎛ ⎛ ωc ⎞ 2 ⎞
⎜1 − ⎜ ⎟ ⎟
⎜ ⎝ω⎠ ⎟
⎝
⎠
0
ω
−j c
ω
1
0
⎤
⎥
0
⎥
⎥ r
0
⎥⋅E
⎥
⎛ ⎛ ωc ⎞ 2 ⎞⎥
⎜1 − ⎜ ⎟ ⎟
⎜ ⎝ ω ⎠ ⎟⎥
⎠⎦
⎝
⎤
⎥
⎥
0
⎥
⎥
⎥
⎥
⎥
⎥ r
0
⎥⋅E
⎥
⎥
⎥
2
N0q
⎥
2
ω 2 mε 0 ⎛⎜ ⎛ ωc ⎞ ⎞⎟⎥
1−
1− ⎜ ⎟ ⎥
2 ⎜
⎛ ⎛ ωc ⎞ ⎞ ⎝ ⎝ ω ⎠ ⎟⎠⎥
⎜1 − ⎜ ⎟ ⎟
⎥
⎜ ⎝ω⎠ ⎟
⎝
⎠
⎦⎥
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
103
Caratterizzazione del plasma
Ponendo:
N0q 2
ωp =
mε 0
come la pulsazionedi plasma allora si ha :
2
⎡
ω
⎛ p⎞
⎜⎜ ⎟⎟
⎢
⎢ 1− ⎝ ω ⎠
2
⎢
⎛ω ⎞
⎢
1− ⎜ c ⎟
⎢
⎝ω⎠
2
⎢
ω
⎛ p⎞
⎢
⎜⎜ ⎟⎟
v
ω
⎢
ω
IV ) ∇ × H = jωε 0 ⎢− j ⎝ ⎠ 2 c
⎢ 1 − ⎛⎜ ωc ⎞⎟ ω
⎢
⎝ω⎠
⎢
⎢
0
⎢
⎢
⎢
Tensore di permittività
⎢
⎣
Davide Micheli
⎛ ωp ⎞
⎜⎜ ⎟⎟
⎝ω ⎠
2
ωc
j
2
⎛ ωc ⎞ ω
1− ⎜ ⎟
⎝ω⎠
2
ω
⎛ p⎞
⎜⎜ ⎟⎟
⎝ω ⎠
1−
⎛ω ⎞
1− ⎜ c ⎟
⎝ω⎠
2
0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
⎤
⎥
⎥
0
⎥
⎥
⎥
⎥
⎥
⎥ r
0
⎥⋅E
⎥
⎥
2⎥
⎛ ωp ⎞ ⎥
1 − ⎜⎜ ⎟⎟
⎝ω ⎠ ⎥
⎥
⎥
⎥
⎦
104
Caratterizzazione del plasma
Pertanto l’equazione di Maxwell diviene:
r
r
~
∇ × H = jωε 0ε ⋅ E
con ε~
tensore di permittività.
Gli elementi fuori dalla diagonale principale del tensore permittività non sono
nulli e si dimostra in tal caso che il mezzo (plasma) è anisotropo, l’anisotropia
nasce dal fatto che vi è la presenza di un campo magnetico esterno quello
terrestre.
Poste le quantità:
⎛ ωp ⎞
⎛ ωp ⎞
⎜⎜ ⎟⎟
⎜⎜ ⎟⎟
ω⎠
ω ⎠ ωc
⎝
⎝
ε1 =1−
; ε2 =
;
2
2
⎛ ωc ⎞ ω
⎛ ωc ⎞
1−⎜ ⎟
1−⎜ ⎟
⎝ω⎠
⎝ω⎠
2
Davide Micheli
2
⎛ ωp ⎞
ε3 =1−⎜⎜ ⎟⎟ ;
⎝ω⎠
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
105
Caratterizzazione del plasma
Allora le equazioni di Maxwell nel plasma divengono:
⎛ ⎡ ε1
⎜⎢
r
r
~
I)
∇ ⋅ D = ∇ ⋅ ε E = ∇ ⋅ ⎜ ⎢ − jε 2
⎜⎢ 0
⎝⎣
r
r
II ) ∇ ⋅ B = ∇ ⋅ H = 0
r
r
III ) ∇ × E = − jωµ 0 H
⎡ ε1
r
IV ) ∇ × H = jωε 0 ⎢⎢ − jε 2
⎢⎣ 0
Davide Micheli
jε 2
ε1
0
jε 2
ε1
0
0⎤ ⎞
r⎟
⎥
0 ⎥E⎟ = ρ = 0
ε 3 ⎥⎦ ⎟⎠
0⎤
r
⎥
0⎥E
ε 3 ⎥⎦
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
106
Caratterizzazione del plasma
Frequenza di ciclotrone:
qB 0
≅ 1 .3
fc =
2π m
MHz
q = 1 .6 ⋅ 10 −19 C
B0 ≅ 0 .46 ⋅ 10 − 4 Wb / m 2
m = 9 .1 ⋅ 10 − 31 Kg
(nostra
latitudine
)
Frequenza di plasma:
1
fp =
2π
N0 q 2
≅ 9 N0 ≅ 10 MHz (se l ' angolo d ' incidenza è di 0°)
mε 0
N0 ≅ 1012 elettroni/ m3
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
107
Caratterizzazione del plasma
Facendo l’ipotesi di lavorare a frequenze f >> fc il tensore di permittività si può
approssimare ad una matrice diagonale in cui tutti i termini sono uguali.
L’onda E.M. vede pertanto un mezzo isotropo caratterizzato da una certa
frequenza di taglio che è detta frequenza di plamsa ed il tensore di permittività
diviene uno scalare che è la costante dielettrica relativa ε.
2
⎡
ω
⎛ p⎞
⎜⎜ ⎟⎟
⎢
⎢ 1− ⎝ ω ⎠
2
⎢
ω
⎛
⎞
⎢
1− ⎜ c ⎟
⎢
⎝ω⎠
2
⎢
⎛ ωp ⎞
⎢
⎜⎜ ⎟⎟
v
ω
⎢
ω
IV) ∇× H = jωε0 ⎢− j ⎝ ⎠ 2 c
⎢ 1− ⎛⎜ ωc ⎞⎟ ω
⎢
⎝ω⎠
⎢
⎢
0
⎢
⎢
⎢
⎢
⎣
⎛ ωp ⎞
⎜⎜ ⎟⎟
ω ⎠ ωc
⎝
j
2
⎛ ωc ⎞ ω
1− ⎜ ⎟
⎝ω⎠
2
⎛ ωp ⎞
⎜⎜ ⎟⎟
⎝ω⎠
2
1−
⎛ω ⎞
1− ⎜ c ⎟
⎝ω⎠
2
0
Davide Micheli
⎤
⎥
0 ⎥⎥
⎥
2
⎡
⎤
f
⎛
⎞
p
⎥
⎢1− ⎜⎜ ⎟⎟
0
0 ⎥
⎥
⎢ ⎝ f ⎠
⎥
⎥
2
⎢
⎥ r
fp ⎞
⎛
⎥ r
0 ⎥ ⋅ E = jωε0 ⎢ 0
1− ⎜⎜ ⎟⎟
0 ⎥⋅ E
⎢
⎥
⎝ f ⎠
⎥
2⎥
⎢
⎥
f
⎛
⎞
p
⎢ 0
0
1− ⎜⎜ ⎟⎟ ⎥
2⎥
⎢
⎛ ωp ⎞ ⎥
f ⎠⎥
⎝
⎣
⎦
1− ⎜⎜ ⎟⎟
⎥
⎝ω⎠
⎥
⎥
⎥
⎦
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
108
Caratterizzazione del plasma
L’equazione di Maxwell pertanto è:
⎡ ⎛ f p ⎞2 ⎤ r
r
v
IV ) ∇ × H = jωε 0 ⎢1 − ⎜⎜ ⎟⎟ ⎥ E = jωε 0ε r E
⎢⎣ ⎝ f ⎠ ⎥⎦
La costante di fase per la propagazione delle onde piane nel plasma uniforme
dipende dalla frequenza in modo non lineare ed il mezzo ionosferico è
pertanto dispersivo.
β≡
ω
u
=
2πf 2π
2πf
=
= 2πf n ε 0 µ0 = 2πf ε r ε 0 µ0 = ω ε µ0
n = β0 n =
c
1
λ0
n
n ε 0 µ0
⎛ fp ⎞
= 2πf 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
⎛ fp ⎞
ε 0 µ0 = K0 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
u = velocitàdi fase
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
109
Caratterizzazione del plasma
Se f < fp β diviene immaginaria e non si ha propagazione attraverso la
ionosfera: l’onda elettromagnetica riflessa dalla ionosfera ritorna a terra
attenuata.
e− j ( jβ )z = e− βz
⇓
attenuazione del segnalelungo la direzione di propagazione ẑ
Se f > fp β diviene reale e l’onda perfora la ionosfera e non rientra a terra:
e− j ( β )z = e− jβz
⇓
propagazione del segnalelungo la direzionedi propagazione ẑ
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
110
Caratterizzazione del plasma
Se f < fp , l’onda E.M. vede un carico reattivo e viene riflessa, non si tratta di
perdite in quanto si è esclusa la presenza di collisioni, la collisione tra
elettroni e molecole è un meccanismo di perdita perché l’energia cinetica
acquistata viene persa come energia assorbita. Nel caso di riflessione, il
rapporto tra campo elettrico e campo magnetico da un impedenza
immaginaria, come un una guida d’onda sotto la frequenza di taglio che nella
ionosfera è la frequenza di plasma.
Se f > fp β diviene reale e l’onda perfora la ionosfera e non rientra a terra:
Se f=fp l’indice di rifrazione si annulla è la
Velocità di fase tende ad infinito
Vfase
c=
1
µ0ε0
fplasma
Davide Micheli
f
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
111
Caratterizzazione del plasma
ionosfera
Nel caso si voglia sfruttare la riflessione ionosferica allora f < fp.
Il grafico è riportato per un onda che viene lanciata verticalmente,
normalmente tuttavia l’onda viene lanciata ad una certa inclinazione che è
funzione della distanza che si vuole raggiungere. Il lancio obliquo riduce il
limite stringente sulla massima frequenza usabile che diviene circa 3 o 4 volte
la fp
f < fp
f > fp
Terra
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
112
Caratterizzazione del plasma
per le velocità di fase e di gruppo si ha:
up =
ω
=
β
2πf
⎛f ⎞
2πf 1 − ⎜⎜ p ⎟⎟
⎝ f ⎠
=
2
ε 0 µ0
c
⎛f ⎞
1 − ⎜⎜ p ⎟⎟
⎝ f ⎠
2
and u p =
1
µε
=
1
1
µ0ε 0
µrε r
=c
1
µrε r
=
c
εr
=
c
n
µr = 1
⎛ω ⎞
1 − ⎜⎜ p ⎟⎟
2
⎛ ωp ⎞
⎝ω ⎠
=c
= c 1 − ⎜⎜ ⎟⎟
2
2
⎡ ⎛ ωp ⎞ ⎤ ⎛ ωp ⎞
⎝ω ⎠
⎢1 − ⎜⎜ ⎟⎟ ⎥ + ⎜⎜ ⎟⎟
⎢⎣ ⎝ ω ⎠ ⎥⎦ ⎝ ω ⎠
2
ug =
•
•
1
1
c
dω
=
=
=
2
2
dβ dβ
⎡
⎤
⎡
ωp ⎞ ⎤
⎛ fp ⎞
⎛
d
d ⎢
⎢ω 1 − ⎜ ⎟ ⎥
2πf 1 − ⎜⎜ ⎟⎟ ε 0 µ0 ⎥
dω
⎜ω ⎟ ⎥
⎥ dω ⎢
dω ⎢
f ⎠
⎝
⎝ ⎠ ⎦
⎣
⎦
⎣
La velocità di fase non ha un significato fisico in quanto ad essa non è associato nessun trasporto
di energia o contenuto informativo del segnale, dalla formula si nota che può essere anche
superiore alla velocità della luce c.
La velocità di gruppo non è mai maggiore della velocità della luce ed è con tale velocità che si
propaga il segnale associato all’onda E.M. Dall’equazione si nota che all’aumentare di ω la velocità
di gruppo ug aumenta. Di conseguenza le frequenze più alte viaggiano più velocemente nella
ionosfera.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
113
Caratterizzazione del plasma
Ipotesi:
1. Direzione di propagazione lungo l’asse z longitudinale, cioè parallela alla
direzione del campo di induzione magnetica esterno B . Le proprietà di
propagazione ionosferica vengono rappresentate bene da questa ipotesi.
scopo:
1. Determinare la costante di propagazione β cioè vedere come un onda
elettromagnetica si propaga all’interno della ionosfera
r r − jβz
E = Et e
r r − jβz
H = Ht e
con
con
r
Et = Ex xˆ + Ey yˆ
r
Ht = Hx xˆ + Hy yˆ
y
Ex
dove
te ano
n
i
o
Fr a p
nd
o
d’
Et
Ey
z
Ex , Ey , Hx , Hy = cost
Ht
x
Davide Micheli
Hy
Hx
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
114
Caratterizzazione del plasma
Sostituendo nelle equazioni di Maxwell si ha:
(
)
(
)
r
r − jβz
∇× E = ∇× Et e
⎡ xˆ
yˆ
zˆ ⎤
⎥
⎢
r
∂
∂
∂
j
z
−
β
⎥ = jβe (Ey xˆ − Ex yˆ ) = jβ Et × zˆ e− jβz
=⎢
∂y
∂z ⎥
⎢ ∂x
⎢E e− jβz E e− jβz 0 ⎥
y
⎦
⎣ x
(
)
r
r
∇× H = jβ Ht × zˆ e− jβz
Sostituendo nelle equazioni di Maxwell trovate per il plasma:
r
r
III) ∇× E = − jωµ0H
⎡ ε1 jε2 0 ⎤
r
r
⎢
⎥
IV) ∇× H = jωε0 ⎢− jε2 ε1 0 ⎥ E
⎢⎣ 0
0 ε3 ⎥⎦
Davide Micheli
r r − jβz
Er = Ert e
H = Ht e− jβz
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
115
Caratterizzazione del plasma
(
)
r
r
r − jβ z
− jβ z
= − j ωµ 0 H t e
III ) ∇ × E = j β E t × zˆ e
(
)
r
r
IV ) ∇ × H = j β H t × zˆ e − j β z
⎡ ε1
= j ωε 0 ⎢⎢ − j ε 2
⎢⎣ 0
jε 2
ε1
0
0⎤
r − jβ z
⎥
0 ⎥ Ete
ε 3 ⎥⎦
Considerando le componenti trasversali ( ONDA T.E.M.) e sostituendo la III
nella IV equazione si ha:
(
)
(
ωµ
)
r −β r
⇒ Ht =
Et × zˆ
r
r
III) β Et × zˆ = −ωµ0Ht
0
⇓
r
⎛ −β r
⎞
⎡ ε1 jε2 ⎤ r
IV) β Ht × zˆ = β ⎜⎜
Et × zˆ × zˆ ⎟⎟ = ωε0 ⎢
Et
⎥
⎣− jε2 ε1 ⎦
⎝ ωµ0
⎠
(
)
(
)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
116
Caratterizzazione del plasma
IV ) - β
2
⇓
r
⎡ ε1
2
Et × zˆ × zˆ = ω µ0ε 0 ⎢
⎣− jε 2
⇓
[(
) ]
r
ε1
2⎡
IV ) - β − Et = K0 ⎢
⎣− jε 2
2
[ ]
jε 2 ⎤ r
Et
⎥
ε1 ⎦
jε 2 ⎤ r
Et
⎥
ε1 ⎦
K0 = ω µ0ε 0
ma
⎡1 0⎤ ⎡β 2
ma lo scalareè β = β ⎢
=⎢
⎥
⎣0 1⎦ ⎣ 0
2
2
0⎤
2⎥
β ⎦
⇓
⎡β 2
IV ) ⎢
⎣0
0 ⎤ r ⎡ K02ε1
E =⎢
2
2⎥ t
jK
−
β ⎦
0ε2
⎣
jK02ε 2 ⎤ r
⎥ Et
2
K 0 ε1 ⎦
⇓
⎡β 2 − K02ε1 − jK02ε 2 ⎤ r
IV ) ⎢
E =0
2
2
2 ⎥ t
β − K 0 ε1 ⎦
⎣ jK0 ε 2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
117
Caratterizzazione del plasma
Una soluzione mediante gli autovalori della matrice si trova ponendo il
determinante della matrice uguale a zero:
⎡β 2 − K02ε1 − jK02ε 2 ⎤
=0
det⎢
2
2
2 ⎥
β − K 0 ε1 ⎦
⎣ jK0 ε 2
β 2 − K02ε1 = ± K02ε 2
⇒
⇒
(β
β 2 = K02 (ε1 ± ε 2
2
−K ε
) − (K ε )
2
2
0 1
2
2
0 2
=0
)
Pertanto si hanno due possibili costanti di propagazione.
⎧β + = K0 ε1 + ε 2 ⎫
⎪
⎪
⎨
⎬
⎪⎩β − = K0 ε1 − ε 2 ⎪⎭
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
118
Caratterizzazione del plasma
Per determinare il tipo di polarizzazione che l’onda che attraversa il plasma
ottiene, è sufficiente trovare le relazione tra le componenti trasverse del
campo elettrico ovvero gli autovettori della matrice:
⎡β 2 − K02ε1 − jK02ε2 ⎤ r ⎡β 2 − K02ε1 − jK02ε2 ⎤⎡Ex ⎤
=0
IV) ⎢
E =⎢
2
2
2 ⎥ t
2
2
2 ⎥⎢ ⎥
⎣ jK0ε2 β − K0ε1⎦
⎣ jK0ε2 β − K0 ε1⎦⎣Ey ⎦
⇓
(β
)
jK ε E + (β
2
− K02ε1 Ex − jK02ε2Ey = 0
2
0 2 x
2
)
− K02ε1 Ey = 0
Considerando per esempio la prima delle 2 eq. ottenute e sostituendo le due
costanti di propagazione β+ e β- trovate si ottiene:
(β
(β
2
+
2
−
)
− K ε )E
− K 02ε1 Ex − jK 02ε 2 E y = 0
2
0 1
Davide Micheli
x
− jK 02ε 2 E y = 0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
119
Caratterizzazione del plasma
Segue che:
β +2 Ex − K02ε1Ex − jK02ε 2 E y = 0
β −2 Ex − K02ε1Ex − jK02ε 2 E y = 0
⇓
In un caso le componenti
2
2
2
K0 (ε1 + ε 2 )Ex − K0 ε1Ex − jK0 ε 2 E y = 0
del campo sono uguali in
ampiezza e sfasate di 90°,
K02 (ε1 − ε 2 )Ex − K02ε1Ex − jK02ε 2 E y = 0
nell’altro caso sono uguali
⇓
in ampiezza e sfasate di 2
2
2
2
K0 ε1Ex + K0 ε 2 Ex − K0 ε1Ex − jK0 ε 2 E y = 0
90°
K02ε1Ex − K02ε 2 Ex − K02ε1Ex − jK02ε 2 E y = 0
⇓
Polarizzazione
E
⎧
⎫
2
2
circolare
x
+
−
=
⇒
=
K
ε
E
jK
ε
E
0
j
0 2 y
⎪⎪ 0 2 x
⎪⎪
Ey
⎨
⎬
Ex
2
2
⎪− K0 ε 2 Ex − jK0 ε 2 E y = 0
⇒
= − j⎪
Ey
⎪⎩
⎪⎭
Pertanto un campo elettromagnetico trasverso che si propaga nel plasma è
caratterizzato dall’avere una polarizzazione circolare in un senso o nell’altro a
seconda dell’autovalore β con la quale si propaga
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
120
propagazione onda T.E.M. nel Plasma
qualitativamente la polarizzazione circolare che vede la rotazione dei vettori
campo elettrico E e di quello magnetico H si può immaginare come disegnato:
y
Ey
te no
n
o pia
r
F a
nd
o
d’
Hx
z
x
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
121
Onda polarizzata linearmente nel Plasma
Un campo E.M. polarizzato linearmente sul piano z=0 può essere lanciato da
un’antenna filiforme. Si supponga che il campo elettrico sia polarizzato su tale
piano lungo la direzione x , questo campo può essere visto come la somma di
due onde polarizzate circolarmente in modo tale che le due componenti lungo
la direzione y si elidano.
E0 pertanto si può immaginare come la somma di due vettori controrotanti e
tali che la loro composizione vettoriale dia un campo elettrico sempre
polarizzato lungo l’asse x con delle componenti orizzontali che si elidono e
delle componenti verticali che si sommano lungo la direzione x .
r
E0 − jβz
E0 − jβz
ˆ
ˆ
ˆ
ˆ
ˆ
E = E0 x = (x + jy ) e + (x − jy ) e
2
2
sul piano z = 0
x
E0/2
β-
E0/2
z
β+
y
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
122
Onda polarizzata linearmente nel Plasma
Nel plasma ionosferico è stato detto nelle ipotesi iniziali che si considerano
solo le cariche rapprentate dagli elettroni q=1.6*10-19 C,
1. quando l’onda elettromagnetica investe la ionosfera, la carica q è
sottoposta al campo elettrico Ex, pertanto esisterà una forza di Lorentz che
agisce sulla carica nella direzione x del campo:
r
F = qEx xˆ
2. è presente anche il campo magnetico B0 terrestre, e dal momento che la
carica è accellerata ed acquista una veloctà V allora sulla carica stessa si
eserciterà anche la forza di Lorentz dovuta al campo magnetico esterno:
r1 v r
F = qV × B0
che è un forza diretta ortogonalmente sia ad F (prodotta da Ex) sia a B0 ,
pertanto il movimento risultante sul piano trasverso sarà rotatorio mentre
più in generale descriverà una spirale
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
123
Onda polarizzata linearmente nel Plasma
x
r
F = qE x xˆ
z
B0
r1
v r
F = q V × B0
y
Moto a spirale
lungo l’asse z
In un caso la rotazione della carica sarà solidale con la rotazione del campo
elettrico in una delle due polarizzazioni, e nell’altro caso sarà controrotante.
Prendiamo in considerazione solo il campo magnetico terrestre in quanto nella
linearizzazione si è fatta l’ipotesi di piccoli segnali, pertanto le forze di Lorentz
dovute al campo magnetico dell’onda incidente sono trascurabili.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
124
Onda polarizzata linearmente nel Plasma
Dopo un tratto di lunghezza z=l di cammino percorso dall’onda linearmente
polarizzata si ha:
r
E
E
E = ( xˆ + jyˆ ) 0 e− jβ −l + (xˆ − jyˆ ) 0 e− jβ +l
2
2
= xˆ
dopo un tratto z = l
E0 − jβ−l
E
E
E
+ jyˆ 0 e− jβ−l + xˆ 0 e− jβ+l - jyˆ 0 e− jβ+l =
e
2
2
2
2
E0 ⎛ e− jβ−l + e− jβ+l ⎞
E0 ⎛ e− jβ−l − e− jβ+l ⎞
⎟⎟ =
⎟⎟ + yˆ ⎜⎜ j
= xˆ ⎜⎜
2 ⎝
1
2 ⎝
1
⎠
⎠
=
l
j (β+ +β− ) ⎤
E0 − j ( β+ + β− ) 2l ⎡ − jβ−l − jβ+l j ( β + + β− ) 2l
− jβ −l
− jβ +l
2
= e
+e
+ jyˆ e
−e
e
e
⎢ xˆ e
⎥=
2
⎣
⎦
(
)
(
)
l
l
l
l
l
l
− jβ + l + jβ + + jβ − ⎞
− jβ −l + jβ + + jβ −
− jβ +l + jβ + + jβ − ⎞⎤
⎛
E0 − j ( β+ + β− ) 2l ⎡ ⎛ − jβ−l + jβ+ 2l + jβ− 2l
2
2⎟
2
2
2
2⎟
⎜e
ˆ
= e
+e
+
−
j
y
e
⎢ xˆ⎜⎜ e
⎥=
⎟
⎜
⎟
2
⎢⎣ ⎝
⎠
⎝
⎠⎥⎦
= E0e
− j (β+ +β− )
l
2
⎡
l⎞
l ⎞⎤
⎛
⎛
− jΦ1
ˆ
ˆ
(
)
(
)
[xˆ cos Φ2 − yˆ sin Φ2 ]
−
−
−
x
cos
β
β
y
sin
β
β
=
E
e
⎜
⎟
⎜
⎟
+
−
+
−
0
⎢
⎥
2⎠
2 ⎠⎦
⎝
⎝
⎣
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
125
Onda polarizzata linearmente nel Plasma
Dopo un tratto di lunghezza z=l di cammino percorso dall’onda linearmente
polarizzata si ha:
E0 e
− j (β + + β − )
l
2
= E 0 e − jΦ 1 = E 0 e − jβ z
l
Φ 2 = (β + − β − )
2
→ Φ 1 è il ritardo di fase lungo zˆ
varia in funzione della distanza l percorsa
Dopo un tratto z=l si ha ancora un onda polarizzata linearmente in quanto le
componenti in x e y sono in fase (non compare il j davanti al seno) ma hanno
ampiezze differenti date dal valore del coseno e
del seno di Ф2
rispettivamente.
Il ritardo di fase è la media delle costanti di propagazione per la lunghezza z=l
percorsa
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
126
Onda polarizzata linearmente nel Plasma
Si è ottenuto che il campo elettromagnetico si trova ad oscillare su un nuovo
piano di polarizzazione che forma con l’asse x un angolo pari a:
⎛ Ey
θ = arctg ⎜⎜
⎝ Ex
⎞
⎧
l ⎫
l
⎟⎟ = arctg ⎨ - tg ⎡⎢ (β + − β − ) ⎤⎥ ⎬ = − (β + − β − )
2 ⎦⎭
2
⎩ ⎣
⎠
Pertanto l’onda E.M. mentre si propaga lungo z all’interno del plasma
ionosferico, cambia il piano di polarizzazione. Tale rotazione che si ha anche
in altri mezzi anisotropi come le ferriti, è chiamata Rotazione di Faraday.
Tale rotazione non esisterebbe se non fosse presente il campo magnetico
terrestre.
x
E
E
θ
z
θ
E
y
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
127
Onda polarizzata linearmente nel Plasma
Conseguenze della Rotazione di Faraday:
L’onda polarizzata linearmente si divide in due onde polarizzate
circolarmente (raggio ordinario e raggio straordinario) con traiettorie
differenti e diversi indici di rifrazione:
•
•
•
•
•
Se il plasma avesse delle proprietà tutte costanti allora l’onda E.M. cambierebbe
semplicemente il piano di polarizzazione
Purtroppo la ionosfera non è una struttura a densità di carica costante, i due indici di
rifrazione e le due costanti di propagazione variano in modo diverso in funzione della
quota, come conseguenza l’onda polarizzata linearmente si suddivide in due onde
polarizzate circolarmente ognuna della quali subisce un proprio destino
Gli indici di rifrazione sono n+ = (ε1+ ε2)0.5 e n- = (ε1- ε2)0.5.
Tali indici di rifrazione sono funzione della quota, ovvero si ha una stratificazione
dell’indice di rifrazione che provoca la curvatura del raggio singolo, i due raggi hanno
cammini e destini differenti in funzione della quota.
Di conseguenza l’onda è completamene alterata nella propagazione all’interno della
ionosfera e generalmente perde completamente le caratteristiche di polarizzazione lineare
L’onda polarizzata linearmente, dopo rifrazione ionosferica presenta in
generale una polarizzazione ellittica :
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
128
Onda polarizzata linearmente nel Plasma
Conseguenze della Rotazione di Faraday:
Raggio ordinario
N(h)
Raggio straordinario
Polarizzazione
iniziale lineare
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
129
Onda E.M. nel plasma, condizione di rientro a terra
•
•
•
Si vuole analizzare la condizione per il rientro a terra di un onda E.M. lanciata
obliquamente, rispetto al piano tangente alla sup. terrestre, nella ionosfera.
Si supponga che la ionosfera sia un mezzo stratificato in cui ogni strato è
caratterizzato da un indice di rifrazione variabile con la quota.
Negli strati bassi dell’atmosfera si suppone un indice di rifrazione unitario, l’indice di
rifrazione per gli altri strati, trovato precedentemente è funzione della quota (h) e
quindi dello strato preso in considerazione:
2
⎛ N0q 2 ⎞
⎜
⎟
2
⎛ fp ⎞
mε 0 ⎟
N0q 2
c
N ( h)
⎜
= ε r = 1 − 80.6 2 = 1 − ⎜⎜ ⎟⎟ = 1 − ⎜
= 1−
n( h) =
⎟
f
mε 0 f 2
v fase
f
⎝f ⎠
⎜⎜
⎟⎟
⎝
⎠
•
•
•
la velocità di fase cresce all’aumentare della densità N0
per ogni frequenza f, l’indice di rifrazione n decresce all’aumentare della densità N0
quando n si annulla l’onda viene riflessa per disadattamento del carico
Per ogni quota z a cui corrisponde una certa densità N si ha che maggiore è la
frequenza f, più è prossimo ad 1 l’indice di rifrazione n, cioè l’onda elettromagnetica
tende a propagarsi come se fosse nel vuoto, cioè perfora la ionosfera.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
130
Onda E.M. nel plasma, condizione di rientro a terra
•
•
Immaginando di inviare un segnale da terra verso il satellite, e supponendo che la
traiettoria iniziale sia verticale, allora inizialmente il segnale incontrerà strati
dell’atmosfera nei quali N≈0 e quindi la propagazione avverrà come nel vuoto in
modo rettilineo. All’aumentare della concentrazione N con la quota, si avrà che la
velocità di fase vf cresce ed n decresce, quindi il segnale passa attraverso regioni
con indice di rifrazione più piccolo e ciò produce un aumento dell’angolo formato
tra la verticale e la direzione di propagazione.
L’indice di rifrazione si annulla quando:
N0q 2
=1
2
mε 0 f
⇒
f = fp
⇒
n=0
questa esprime la condizione di riflessione del segnale che non si propaga in
avanti, di conseguenza per ogni N e quindi per ogni quota z, esiste una frequenza fc
o frequenza critica che esprime la massima frequenza che può essere riflessa, per
esempio
regione D dove N≈103 /cm3 si ha fc=280 KHz
regione F dove N≈2x106 /cm3 si ha fc=13 Mhz
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
131
Onda E.M. nel plasma, condizione di rientro a terra
•
Un modello stratificato di indice di rifrazione è adatto per applicare la legge di
Snell, supponendo la propagazione per raggi si ha pertanto:
n(h) ⋅ senΦ(h) = n(0) ⋅ senΦ(0)
hp : n(0) = 1
⇓
n(h) ⋅ senΦ(h) = 1⋅ senΦ(0) ⇒ Φ(h) = arcsen
Davide Micheli
1⋅ senΦ(0)
n( h)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
132
Onda E.M. nel plasma, condizione di rientro a terra
Aumentando la quota h aumenta la densità N di elettroni fino a raggiungere
una quota hmax in corrispondenza della quale si ha la massima densità Nmax,
dopodichè N tende di nuovo a diminuire.
Se N aumenta, allora dalla espressione dell’indice di rifrazione si vede che
l’indice di rifrazione n si riduce, cioè si passa da un mezzo più denso ad uno
meno denso di conseguenza l’angolo Ф con la verticale aumenta e la traiettoria
del raggio si inclina verso il basso.
Ф(hn)
h
Ф(hi)
Ф(0)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
133
Onda E.M. nel plasma, condizione di rientro a terra
Si possono analizzare ora due casi:
f < fp e f > fp
1) f < fp
allora l’onda e.m. vede sempre un carico puramente reattivo e quindi
l’onda comunque ritorna verso terra. Il valore dell’indice di rifrazione n(h)
pertanto raggiunge sempre il valore zero ad una quota inferiore a quella
per cui si ha il massimo valore di N(h)=Nmax cioè n=nmin. Di conseguenza
esisterà sicuramente una quota dove il raggio è orizzontale cioè Ф=π/2.
L’onda in corrispondenza di tale punto viaggia orizzontalmente per poi
rientrare a terra in quanto continuando a salire tale angolo aumenta
ancora.
Se rientra verso terra un onda lanciata verticalmente a maggior ragione
rientra un onda lanciata obliquamente.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
134
Onda E.M. nel plasma, condizione di rientro a terra
2) f >fp
Se l’onda fosse lanciata verticalmente perforerebbe la ionosfera. Dal
momento che l’onda viene lanciata obliquamente allora la condizione di
rientro a terra cioè onda viaggiante orizzontalmente Ф=π/2 deve verificarsi
ad una quota minore alla quota dove si raggiunge la massima densità N
ovvero il minimo indice di rifrazione n.
Infatti in ogni strato l’onda subisce una deflessione in quanto l’indice di
rifrazione è via via decrescente, e quindi aumenta l’angolo di
propagazione, si hanno i seguenti casi:
–
Se non raggiungo la propagazione orizzontale prima che n divenga minimo
allora in corrispondenza di strati superiori a quello con n minimo, l’angolo di
deflessione si riduce di nuovo perché si inverte la tendenza di n, ed in tal caso
l’onda non rientra più a terra.
nminimo
Ф(hn)
h
Ф(hi)
nmassimo
Ф(0)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
135
Onda E.M. nel plasma, condizione di rientro a terra
–
Se l’onda raggiunge la propagazione orizzontale prima che si
raggiunga la quota dello strato con n minimo allora, continuando a
salire, l’indice di rifrazione si ridurrebbe ulteriormente perchè lo strato
superiore è maggiore densità e quindi l’angolo aumenta ancora e
l’onda rientra verso il basso.
nminimo
Ф(hn)
h
Ф(hi)
Ф(h) aumenta
Ф(0)
nmassimo
modello a raggi delle onde elettromangetiche
ed applicazione della legge di Snell
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
136
Onda E.M. nel plasma, condizione di rientro a terra
Dalla legge di Snell segue :
n(h) ⋅ senΦ(h) = n(0) ⋅ senΦ(0)
hp : n(0) = 1
hM deve essere inferiore
alla quota per cui n=nmin
Φ(hM ) = π / 2
⇓
n(hM ) ⋅ sen(π / 2) = 1⋅ senΦ(0)
⇓
n(hM ) = senΦ(0) ≥ nmin
Essendo nmin pari a:
n min
fp
81 N max
≅ 1−
= 1− 2
2
f
f
Davide Micheli
⇒
sen Φ (0) ≥ 1 −
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
fp
f
2
137
Onda E.M. nel plasma, condizione di rientro a terra: massima
frequenza usabile
La massima frequenza usabile è pari a:
senΦ(0) ≥ 1 −
cos Φ(0) ≥
2
fp
f
2
fp
f
⇒
2
⇒
sen Φ(0) ≥ 1 −
2
f max ≤
fp
f
fp
cos Φ(0)
2
2
⇒
1 - sen Φ(0) ≥
2
fp
f2
= Maximum Usable Frequency
La frequenza di lavoro deve essere minore della fmax al fine di ottenere il
rientro a terra.
La fmax dipende dalla frequenza di plasma e dall’angolo di incidenza, quando
l’angolo di incidenza è nullo la massima frequenza usabile diviene minore di
quella di plasma, qualora invece l’onda e.m. incida obliquamente la
frequenza usabile può essere maggiore della frequenza di plasma
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
138
Onda E.M. nel plasma, condizione di rientro a terra: massima
frequenza usabile
La frequenza di lavoro deve essere la più elevata possibile per :
–
–
–
ridurre le perdite
Ridurre la dispersione
Ridurre l’anisotropia che dipende dalla frequenza di ciclotrone,
pertanto più la frequenza è maggiore della frequenza di ciclotrone
tanto più ridotta è l’anisotropia del plasma.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
139
Onda E.M. nel plasma, condizione di rientro a terra: massima
frequenza usabile: esempio di onda radente
Si supponga di lanciare un onda elettromagnetica tangenzialmente rispetto
alla superficie terrestre;
Si deve tenere presente la curvatura della superficie terrestre;
Si supponga che la stratificazione ionosferica sia concentrica rispetto alla
curvatura terrestre
L’angolo di incidenza è formato tra la direzione di propagazione dell’onda e
la verticale della terra e vale:
Ф
r = (r + h )sen Φ = (6370 Km + 300 Km )sen Φ
Tx
90
⇓
⎛ r ⎞
Φ = arcsen ⎜
⎟ ≅ 73 ° ⇒
⎝r+h⎠
MUF =
fp
cos Φ
arcoT x R x = 2 ⋅ α ⋅ r = 2 ⋅ (180 − 90 − Φ ) ⋅ r
≅ 2 ⋅ (180 − 90 − 73 ° ) ⋅ 6370 = 4000 Km
Davide Micheli
≅ 3 .5 f p
Rx
r+h
r
α
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
140
Onda E.M. nel plasma, condizione di rientro a terra: massima
frequenza usabile: esempio di onda radente
Questo è il motivo perché Marconi fu fortunato nel suo esperimento di
comunicazione tra l’Inghilterra e l’isola di terranova: lavorò a frequenze
sufficientemente basse per sfruttare questo fenomeno di rifrazione ionosferica.
La cosa non sarebbe avvenuta se avesse utilizzato delle frequenze dell’ordine
di quelle usate da Hertz nei suoi esperimenti in cui dimostro la veridicità delle
equazioni di Maxwell verificando l’esistenza delle onde elettromagnetiche.
L’esperimento di Marconi getto in subbuglio il mondo scientifico di allora in
quanto Hertz aveva dimostrato che l’onda elettromangetica esisteva e si
propagava in linea retta; Marconi con il suo esperimento mostrò che le onde
elettromagnetiche apparentemente seguivano la superficie terrestre in quanto
lanciate con un certo angolo erano arrivate, seguendo la ionosfera in un altro
punto della terra rispettando la curvatura terrestre invece di proseguire in
modo rettilineo.
Heaviside fu uno dei primi a supporre che ci fosse qualche cosa nell’atmosfera
che spiegasse il comportamento delle onde elettromagnetiche che vi si
propagavano
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
141
Onda E.M. nel plasma, ionogrammi
Può essere comodo definire anziché una curvatura ad opera della rifrazione
degli strati della ionosfera, una curvatura dovuta alla riflessione totale degli
strati.
Senza ulteriormente approfondire tale metodo di calcolo di tratta, si mette
tuttavia in evidenza la possibilità di definire l’altezza virtuale di ogni strato.
Si immagini di lanciare l’onda verticalmente con angolo Ф=0° allora se τg è il
tempo di ritardo di gruppo, la quota virtuale hvirt e la densità degli elettroni
N(hvirt) si determina nel modo sotto:
c ⋅τ g
c ⋅τ g
c ⋅τ g
=
hvirt =
=
2 cos(Φ 0 ) 2 cos(0)
2
⇓
fp
fp
M .U .F =
=
= fp
cos(Φ 0 ) cos(0)
⇓
f p ≅ 9 N (hvirt )
⇓
⎛ fp ⎞
N (hvirt ) ≅ ⎜⎜ ⎟⎟
⎝ 9 ⎠
Davide Micheli
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
142
Onda E.M. nel plasma, ionogrammi
Utilizzando varie frequenza da lanciare verticalmente si può risalire dal tempo
di ritardo τg di riflessione per ogni frequenza, corrispondenti alla quota alla
quale si trovano gli strati riflettenti.
Dal momento che oltre la frequenza di plasma l’onda perfora la ionosfera e
non rientra più a terra, allora è possibile determinare la frequenza di plasma
come la massima frequenza trasmessa oltre la quale il segnale non è più
ricevuto a terra.
Una volta nota fp si può poi studiare la densità N di elettroni presenti nei vari
strati della ionosfera (ionogrammi)
In tale studio si fa l’ipotesi che la velocità di propagazione nella ionosfera sia
pari a quella della luce nel vuoto “c”, in realtà tale velocità è più bassa.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
143
Ionospheres
The vertical structure of the
Earth ionosphere.
The figure shows the main source
of ionizing radiation at each layer
(D, E, F1,F2), the main ionized
species and the plasma density n.
Max density
Typical temperatures of the
ionospheric plasma:
E=KT=0.1 -- 0.3 eV
T=0.1 x 11600=1600 K
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
144
Vertical Incidence Soundings (Ionograms)
•
•
•
•
Ionograms are recorded tracings of reflected high frequency radio pulses generated by an ionosonde.
Unique relationships exist between the sounding frequency and the ionization densities which can
reflect it. As the sounder sweeps from lower to higher frequencies, the signal rises above the noise of
commercial radio sources and records the return signal reflected from the different layers of the
ionosphere.
These echoes form characteristic patterns of "traces" that comprise the ionogram. Radio pulses travel
more slowly within the ionosphere than in free space, therefore, the apparent or "virtual" height is
recorded instead of a true height. For frequencies approaching the level of maximum plasma frequency
in a layer, the virtual height tends to infinity, because the pulse crosses the ionosphere and does not
come back. The frequencies at which this occurs are called the critical frequencies
Characteristic values of virtual heights (designated as h'E, h'F1, and h'F2, etc.) and critical frequencies
(designated as foE, foF1, and foF2, etc.) of each layer are scaled, manually or by computer, from these
ionograms. Typically, an ionosonde station obtains one ionogram recording every 15 minutes..
The resulting numerical values, along with the original ionograms and station reports, are archived at
five World Data Centers (WDCs) for Ionosphere. The National Geophysical Data Center (NGDC),
which is co-located with the World Data Center for Solar-Terrestrial Physics, Boulder (WDC for STP,
Boulder), has assembled some 40,000 station-months of scaled digital Ionospheric vertical incidence
parameters from about 130 sites worldwide and offers them on CD-ROM
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
145
Definition of the Ionospheric Regions (Structures)
For convenience, we divide the Ionosphere into four broad regions called D, E, F, and topside. These
regions may be further divided into several regularly occurring layers, such as F1 or F2.
•D-Region:
The region between about 75 and 95km above the Earth in which the (relatively weak) ionization is
mainly responsible for absorption of high-frequency radio waves.
•E-Region:
The region between about 95 and 150km above the Earth that marks the height of the regular daytime Elayer. Other subdivisions, isolating separate layers of irregular occurrence within this region, are also
labeled with an E prefix, such as the thick layer, E2, and a highly variable thin layer, Sporadic E. Ions in
this region are mainly O2+.
•F-Region:
The region above about 150km in which the important reflecting layer, F2, is found. Other layers in this
region are also described using the prefix F, such as a temperate-latitude regular stratification, F1, and a
low-latitude, semi-regular stratification, F1.5. Ions in the lower part of the F-layer are mainly NO+ and
are predominantly O+ in the upper part. The F-layer is the region of primary interest to radio
communications.
•Topside:
This part of the Ionosphere starts at the height of the maximum density of the F2 layer of the Ionosphere
and extends upward with decreasing density to a transition height where O+ ions become less numerous
than H+ and He+. The transition height varies but seldom drops below 500km at night or 800km in the
daytime, although it may lie as high as 1100km. Above the transition height, the weak ionization has little
influence on radio signals.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
146
ionograms
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
147
ionograms
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
148
Ionosfera ritardo di propagazione nei segnali GPS
Da Maxwell si ha nel caso di segnali
sinusoidali si ha:
E.M. nel plasma ionosferico
ρ
I) ∇• E =
ε
II) ∇ • B = 0
ϑB
III ) ∇ ∧ E = −
= -jωµ H
ϑt
ϑE
IV) ∇ ∧ B = µ j + µε
= µ j + jωµε E
ϑt
ϑ jωt
ϑ
jωt
dove e = jω ⋅ e ⇒ = jω
ϑt
ϑt
⇓
ϑE
∇ ∧ H = j +ε
= j + jωε E
ϑt
l’equazione del moto per un elettrone libero è:
r
r
r
F = ma = qE + qu × B
r
⎧ F = forza a cui e soggetta la particella in moto ⎫
⎪ q = − 1.6 ⋅ 10 −19 Coulomb carica elettrone
⎪
⎪⎪ m = 9 .1 ⋅ 10 − 31 Kg massa elettrone
⎪⎪
con : ⎨
⎬
u = velocità della particella
⎪
⎪
=
E
campo
elettrico
⎪r
⎪
⎪⎩ B = campo di induzione magnetica
⎪⎭
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
149
Ionosfera ritardo di propagazione nei segnali GPS
Si consideri un gas ionizzato o plasma in cui si propaghi un onda piana di
pulsazione ω polarizzata circolarmente. Trascurando l’effetto del campo
magnetico terrestre, cosa possibile facendo l’approssimazione di
propagazione QL (quasi longitudinale) ovvero propagazione parallela al
campo magnetico terrestre, allora l’equazione del moto per un elettrone libero
si semplifica e diviene dipendente dal solo campo elettrico:
r
r
r
du
ma = m
= jω u m = qE
dt
r q E
⇒ u=
m jω
Se N è il numero di elettroni per metro cubo (densità di elettroni), si ha
dunque la seguente densità di corrente J:
q E
Nq 2 E
J = Nq u = Nq
=
m jω
m jω
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
150
Ionosfera ritardo di propagazione nei segnali GPS
La IV eq di Maxwell diviene allora:
⎛ Nq2 1 ⎞
⎛ Nq2 1 ⎞
Nq2 E
~E
⎟
⎜
⎟
+ jωε 0 E = jωε 0 ⎜⎜1 +
=
−
E
j
ωε
1
E
=
j
ωε
ε
IV) ∇ ∧ H = j + jωε 0 E =
r
0
0
2 ⎟
⎜ mε ω 2 ⎟
m
ε
m jω
(
)
j
ω
0
0
⎝
⎠
⎝
⎠
ε 0 = 8.86 ⋅10−12 [Farad / m] = c.dielettrica vuoto
ε~r = tensore di permittività (è una matrice che indica un mezzo anisotropo)
Definita la frequenza di ciclotrone fc e la frequenza di plasma fp come:
fc =
qB0
2π m
f c = 1.3
1
fp =
2π
f p = 10
con : q = 1.6 ⋅10 -19
B0 = 0.46 ⋅10 − 4
m = 9.1 ⋅10 −31
[C ]
[Wb / m ]
2
[Kg ]
(alla nostra latitudine)
[MHz ]
Nq 2
≅9 N
mε 0
con N = 1012
[e
−
/ m3
]
[MHz ]
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
151
Ionosfera ritardo di propagazione nei segnali GPS
Se la frequenza f è maggiore di fc allora il tensore di permettività (matrice) diviene uno
scalare dipendente dalla frequenza, ed il plasma da mezzo anisotropo diventa un mezzo
isotropo:
⎛ 1 Nq
⎜
2
⎜ 2π mε 0
Nq 1
ε~r = ε r = 1 −
1
=
−
⎜
mε 0 ω 2
f
⎜
⎜
⎝
2
2
⎞
⎟
2
⎡⎛ q ⎞ 2 1 ⎤ N
⎟
⎛ fp ⎞
N
⎟
⎜
1
1
=
1
−
80
.
6
=
−
=
−
⎟
⎢⎜
⎥ 2
⎟
2
⎜ f ⎟
π
ε
2
m
f
f
⎝
⎠
⎢
⎥
⎠
⎝
0
⎟
⎣
⎦
⎟
⎠
l’indice di rifrazione è pertanto:
n = ε r = 1− 80.6
N
N
≅
1
−
81
f2
f2
Il plasma ionosferico è dunque un mezzo dispersivo con indice di rifrazione n variabile
con la frequenza
la frequenza di plasma è appunto quella frequenza per cui l’indice di rifrazione si
annulla:
[
]
f p ≅ 81N = 9 N ≅ 9 1012 e − / m 3 ≈ 10 MHz
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
152
Ionosfera ritardo di propagazione nei segnali GPS
L’indice di rifrazione n può essere espresso come si è visto:
n = ε r = 1 − 80.6
N
f2
⇔
n 2 = 1 − X = 1 − 80.6 ⋅
N
f2
dove N è la densità di elettroni.
Nel caso dell’approssimazione QL (Quasi Longitidinal) X << 1, quindi si
può assumere ( primo termine dello sviluppo in serie ):
np ≅ 1−
X
N
= 1 − 40.3 ⋅ 2
2
f
Allora la differenza di percorso dovuto a ritardo ionosferico è ottenuta da:
ricevitore
∆R
phase
iono
ricevitore
40.3 ⋅ N
(n p −1)dr = ∫ (1 −
=
−1)dr =
2
∫
f
Satellite
Satellite
3
ricevitore
ricevitore
40.3 ⋅ N elettroni/ m
40.3
40.3
elettroni/ m3
= ∫ −
dr = − 2 ∫ N
dr = − 2 TEC
2
f
f Satellite
f
Satellite
Davide Micheli
elettroni/ m3
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
153
Ionosfera ritardo di propagazione nei segnali GPS
dove N è la densità di elettroni (e-/m3), e TEC (Totale Electron Content) è il
contenuto di elettroni in una colonna di sezione pari a 1 m2
In realtà andrebbe considerato il ritardo di gruppo con il corrispondente
indice di rifrazione di gruppo ng , si dimostra che questo è:
X
N
ng = 1 + = 1 + 40.3 ⋅ 2
2
f
Quindi la differenza di percorso risulta:
gruppo
∆Riono
=
40.3
(TEC )
2
f
Che si traduce in una variazione di fase data da
2π
2πf
− 7 (TEC )
∆φ = ∆R ⋅ β = ∆R ⋅
= ∆R ⋅
= 8.44 ⋅10 ⋅
λ
c
f
Davide Micheli
rad
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
154
Ionosfera ritardo di propagazione nei segnali GPS
L’errore di distanza dovuto all’effetto ionosferico è preponderante rispetto a
quello troposferico ed è dell’ordine dei 10 m sulla misura di distanza.
L’attraversamento della ionosfera da parte del segnale GPS comporta sullo
pseudorange basato sulla correlazione di codici, un ritardo di gruppo,
mentre le misure di fase sono caratterizzate da un anticipo di fase. In
entrambi i casi si rappresenta il ritardo ionosferico come una correzione
della misura di distanza che va sommata nel caso dello pseudorange oppure
sottratta nel caso della fase al range geometrico nelle equazioni delle
osservabili.
∆R
fase
iono
1 40.3
1 40.3
=−
N dl = −
TEC
2 ∫ el
2
sinΦ f
sinΦ f
[m]
TEC = Totale elettroni contati
1
= Fattore di obliquità
sin Φ
f = frequenza
utilizzata
[Hz]
TEC (Totale Electron Content) è il contenuto di elettroni in una colonna di
sezione pari a 1 m2 lungo il cammino di propagazione
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
155
Ionosfera ritardo di propagazione nei segnali GPS
Il fattore di obliquità (1/sen Ф) tiene conto dell’incremento di cammino di
propagazione del segnale all’interno della ionosfera qualora la direzione di
propagazione non sia verticale rispetto alla superficie terrestre (zenit). L’angolo
Ф viene normalmente preso alla quota geografica dove il cammino di
propagazione Path Lenght interseca l’altezza media della ionosfera circa 350
Km.
GPS satellite
Direzione
verticale
Ф
io
no
sf
er
a
Rterra
Davide Micheli
Altezza media
Ionosfera= 350 Km
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
156
Ionosfera ritardo di propagazione nei segnali GPS
Effettuando una coppia di misure su due distinte frequenze L1 e L2 si ottiene
la differenza di range (m) causata dal ritardo ionosferico sui segnali a
frequenze L1 e L2:
(
∆ ∆R
)
fase
iono
⎡ 1 40.3
⎤
⎛ 1 ⎞
1 40.3
1
N dr- ⎢−
N dr = −
40.3⋅TEC⋅ ⎜⎜ 2 2 ⎟⎟
=−
2 ∫ el
2 ∫ el ⎥
sinΦ f1
sinΦ
⎣ sinΦ f2
⎦
⎝ f1 − f2 ⎠
Quanto più le frequenze sono differenti tra loro tanto è più apprezzabile la
misura di ritardo.
Dividendo per la velocità media di propagazione, all’interno del plasma
ionosferico, alle due frequenze L1 e L2, si ottiene l’errore sul tempo di ritardo
causato dalla ionosfera.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
157
Ionosfera ritardo di propagazione nei segnali GPS
Alla frequenza di L1 =1575 MHz la ionosfera può ritardare l’onda radio anche
per più di 300 ns rispetto alla propagazione nello spazio libero, tale ritardo si
traduce in 100 m di range error.
Al fine di ridurre tali effetti è stata introdotta come visto una seconda
frequenza L2=1227 MHz che permette al ricevitore di calcolare il ritardo
ionosferico relativo e quindi di correggere gli errori introdotti nelle misure di
range e range rate.
Alcuni ricevitori tuttavia non hanno la possibilità di fare misure su entrambe le
frequenze e quindi per la stima del ritardo ionosferico utilizzano un modello
che si serve di 8 coefficienti trasmessi come parte di un messaggio satellitare.
Tale sistema consente di correggere approssimativamente il 50 % del range
error causato dalla ionosfera. Correzioni sul range rate error viceversa non
sono possibili a causa dell’impossibilità di predire se non in modo statistico le
scintillazioni della ionosfera che causano errori di rate range su finestre
temporali da pochi secondi a qualche minuto.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
158
Ionosfera ritardo di propagazione nei segnali GPS
la percentuale del 50 % di correzione del valore quadratico medio dell’errore
ionosferico è stato un compromesso con il numero dei coefficienti che devono
essere trasmessi dal satellite. Per ottenere infatti una correzione superiore fino al
70% occorrerebbero molti coefficienti.
Tale compromesso dipende più precisamente da:
– Complessità computazionale del ricevitore;
– Conoscenza attuale della variazione temporale, diurna, e geografica del
TEC (Total Electron Content); in particolare si è tenuto conto della
conoscenza del TEC a latitudini medie escluse cioè le zone polari ed
equatoriali dove i ricevitori GPS a singola frequenza sono meno diffusi,
e dove la conoscenza della distribuzione TEC è meno conosciuta. Per
esempio si è constato che il TEC max non si ha all’equatore ma a
latitudini di ± 15° dall’equatore, inoltre il ritardo a 5°di elevazione diviene
3 volte quello allo zenith. Si è visto anche che mediando i dati diurni di
diverse parti della terra si ha un valore medio massimo per il TEC alle
ore 14.00 ora locale con una deviazione standard dalla media mensile
compresa tra il 20% e il 25% per ogni ora del giorno.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
159
Ionosfera ritardo di propagazione nei segnali GPS
–
Numero dei coefficienti disponibili nel messaggio di navigazione per la
correzione del ritardo ionosferico
L’algoritmo incorporato nel sistema GPS per ricevitori a singola frequenza,
consiste in una rappresentazione a coseno della curva diurna del TIME DELAY
la cui ampiezza è larghezza(periodo) dipendono dalla latitudine.
TIME DELAY (ns at 1.6 GHz)
COSINE MODEL
DC term
ACTUAL DATA
35
30
AMPLITUDE
25
20
15
10
PHASE
5
PERIOD / 2
0
0
2
4
6
8
10
12
14
16
18
20
22
24
LOCAL TIME
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
160
Ionosfera ritardo di propagazione nei segnali GPS
La curva a coseno per ricevitori a singola frequenza presenta 4 principali
parametri:
–
–
–
–
Il termine continuo è costante durante la notte (DC term)
L’ampiezza del termine coseno
La fase del termine coseno
Il periodo del termine coseno
Lo studio del termine continuo e della fase ha mostrato che entrambi i termini
possono essere considerati costanti con un piccolo incremento dell’errore
quadratico medio commesso dall’algoritmo.
Così il temine continuo è stato fissato a 5 ns e la fase alle ore 14.00 ora locale.
I rimanenti parametri di ampiezza e periodo sono funzione della latitudine e
sono rappresentati nell’algoritmo da un polinomio di terzo grado. I coefficienti
di tale polinomio sono trasmessi come parte del messaggio satellitare.
Tali coefficienti sono calcolati tramite un modello empirico del comportamento
ionosferico su scala mondiale per ciascun periodo di 10 giorni dell’anno e per
diversi valori di condizioni di flusso solare. Questi coefficienti sono trasmessi
dal satellite GPS e sono aggiornati ogni 10 giorni o a volte più frequentemente
in funzione del flusso solare.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
161
Superfici selettive in frequenza
Applicazione ai segnali RF
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
162
Note su filtri RF: Introduzione
• Supponiamo che un elettrone giaccia su un piano.
• Supponiamo che un onda EM piana con una polarizzazione lineare incida su tale
particella.
• La particella, se libera, inizierà a muoversi secondo la forza esercitata dal Campo
EM. L’equazione che lega il Campo EM in forza agente sulla particella è quella
della forza di Lorents
r
r
r r
F = qE + qv × B
Ipotizziamo due casi di analisi iniziali:
a) l’elettrone all’interno del filtro è libero di muoversi secondo la direzione del
campo elettrico incidente
b) L’elettrone all’interno del filtro si può muovere solo lungo una direzione che è
perpendicolare a quella del campo elettrico incidente
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
163
Note su filtri RF: Introduzione
a)
l’elettrone è libero di muoversi nella direzione del campo elettrico agente
pertanto, l’energia dell’onda EM incidente è utilizzata per il movimento
dell’elettrone. L’elettrone muovendosi crea una corrente elettrica variabile il
quale genera a sua volta un campo EM. Se a valle del filtro il Campo EM
generato è in opposizione di fase rispetto a quello incidente, allora
l’interferenza distruttiva tenderà a cancellare il Campo EM trasmesso
complessivamente a valle del filtro. L’onda EM reirradiata a monte del filtro,
cioè verso la sorgente di emissione è chiamata Campo EM riflesso
Filtro
Filtro
E
E
B
B
Caso a)
Caso b)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
164
Note su filtri RF: Introduzione
b)
l’elettrone non è libero di muoversi nella direzione del campo elettrico agente
pertanto, l’energia dell’onda EM incidente non è utilizzata per il movimento
dell’elettrone. In questo caso tutta l’energia dell’onda incidente si trasmette
alla porta di uscita del filtro.
Filtro
Filtro
E
E
B
B
Caso a)
Caso b)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
165
Note su filtri RF: Introduzione
• Nel caso di filtri basati su superfici metalliche, alcune frequenze saranno
preferite ovvero faranno oscillare gli elettroni con una maggiore efficienza
rispetto ad altre frequenze.
• Il risultato è la frequenza di risonanza del filtro che determina la frequenza di
massima attenuazione dell’onda EM incidente e quindi determina la trasmittanza
e la riflettanza.
Questa frequenza dipende principalmente da:
–
–
–
Materiali utilizzati per la costruzione dei filtri;
Dimensioni rispetto alle lunghezze d’onda utilizzate;
Forma dei percorsi permessi agli elettroni;
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
166
Geometria dei filtri e circuiti equivalenti
• A livello generale vi sono principalmente tre geometrie che di base possono
essere utilizzate per comprendere il funzionamento dei filtri:
–
–
–
STRIP GRATING FILTERS
MASH FILTERS
CROSS-MASH FILTERS
• Il primo tipo di filtri sono efficaci solo su una polarizzazione del campo EM
incidente.
• Gli altri sono efficaci su qualunque polarizzazione lineare e sono usati come filtri
passa banda ed elimina banda.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
167
STRIP GRATING FILTERS
• La geometria è la seguente:
1
2
Strip Grating Induttivo
Strip Grating Capacitivo
g
2a
g
2a
I1
v1
1
I1
I2
ZL
Z L = jωL
Davide Micheli
2
v2
v1
1
I2
ZC
ZC =
2
v2
1
jωC
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
168
STRIP GRATING FILTERS
• Quando un Campo Elettrico variabile viene applicato allora:
1
Strip Grating Induttivo
2
Strip Grating Capacitivo
g
-
E0
E0
+
+
+
+
+
+
+
2a
+
+
+
E0
E0
-
-
-
Davide Micheli
+
+
+
+
+
+
+
+
+
+
-
+
+
+
+
+
+
+
+
+
+
-
+
+
+
+
+
+
+
+
+
+
-
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
+
+
+
+
+
2a
g
+
+
+
+
+
-
169
-
-
STRIP GRATING FILTERS
• Analizziamo lo Strip Grating Capacitivo.
• Consideriamo due frequenze per l’onda EM:
–
–
F1 con lunghezza d’onda λ >> 2a
F2 con lunghezza d’onda λ << 2a
• Essendo F1 sufficientemente bassa allora è
come se gli elettroni rimanessero per un tempo
abbastanza lungo in una situazione stazionaria
ovvero senza muoversi. Se non ci sono
movimenti di cariche allora non vi è neppure
assorbimento di energia e l’onda EM si
propagherà verso la porta di uscita del filtro.
• Essendo F2 sufficientemente alta allora il moto
oscillatorio delle cariche elettriche sarà molto
più veloce. Il passaggio di corrente dovuto al
veloce movimento di cariche testimonia che
l’energia dell’onda EM incidente viene
assorbita maggiormente rispetto al caso
precedente con F1
–
2
Strip Grating Capacitivo
2a
E0
g
2a
E0
g
Le alte frequenze vengono attenuate.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
170
STRIP GRATING FILTERS
• Analizziamo lo Strip Grating Induttivo.
• Consideriamo due frequenze per l’onda EM:
–
–
F1 con lunghezza d’onda λ grande
F2 con lunghezza d’onda λ piccolo
• Con F1 bassa, se il tempo che intercorre tra i
cambi di polarità di E è sufficientemente lungo,
allora gli elettroni hanno il tempo di muoversi
lungo tutto il percorso conduttivo. In questo
caso essi utilizzano l’energia dell’onda EM
incidente che viene pertanto attenuata.
• Con F2 alta, se il periodo di oscillazione è
sufficientemente breve, allora gli elettroni non
hanno il tempo di percorrere lunghe distanze.
In questo modo ad un limitato movimento è
associato un limitato assorbimento di energia.
Di conseguenza l’onda EM incidente si
propaga verso la porta di uscita del filtro.
–
1
Strip Grating Induttivo
g
E0
2a
E0
Le basse frequenze vengono attenuate
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
171
MASH FILTERS
• I Mash Filters sono filtri che possono utilizzare qualunque polarizzazione
lineare dell’onda incidente.
• Lo scheda di questo tipo di filtri è il seguente:
1
2
Mash filter Induttivo
Mash filter Capacitivo
g
2a
g
I1 2a
I2
I1
I2
ZC
ZC
v1
1
ZL
R
Davide Micheli
2
v2
v1
ZL
1
2
v2
R
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
172
MASH FILTERS
• Il principio di funzionamento di questi filtri è lo stesso dei filtri già visti in quanto
rappresenta la loro combinazione.
• In particolare un onda EM polarizzata linearmente in una qualunque direzione
può essere considerata come la somma vettoriale di due onde EM polarizzate
linearmente tra loro sfasate di 90°.
• Ogni componente dell’onda pertanto vedrà un sistema più semplice basato su
STRIP GRATING.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
173
Linee di trasmissione
Note sulla propagazione dei segnali radio
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
174
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Fissato un sistema di riferimento su una linea di trasmissione ( LdT ) con
impedenza caratteristica, chiusa su un generico carico, possiamo scrivere le
equazioni che descrivono l’andamento spaziale dei fasori di tensione e corrente.
Facciamo l’ipotesi che la linea sia non dispersiva (e quindi che le sue proprietà
non variano con f) e priva di perdite ( non c’è perdita di potenza lungo la linea ).
I(l)
+
Zl
Z0
V(l)
-
z
-l
0
Riprendiamo l’equazione dei telegrafisti supponendo una linea senza perdite:
⎧ V (z )z = − l = V + e − j⋅β ⋅ z + V − e + j⋅β ⋅ z
⎧ V (− l ) = V + e j⋅β ⋅l + V − e − j⋅β ⋅l
⎪
⎪
⎪
⎪
⇒
⎨
⎨
+
−
+
−
V
V
V
V
j
l
⋅
β
⋅
− j ⋅β ⋅l
j
z
j
z
−
⋅
β
⋅
+
⋅
β
⋅
⎪ I (− l ) =
⎪I (z )
e
e
−
e
e
=
−
z =−l
⎪⎩
⎪⎩
Z0
Z0
Z0
Z0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
175
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Dove:
β=
ω
v
=
2π
λ
vF
λ=
f
= ω µε
vF =
c
εR
V += fasore dell’onda di tensione incidente
V −= fasore dell’onda di tensione riflessa
Costante dielettrica
β= costante di fase
VF=velocità di fase dell’onda
•Sul piano di riferimento
(l = 0)
si ha:
I(l)
+
Zl
Z0
V(l)
-
z
-l
0
Davide Micheli
⎧V (0 ) = V + + V −
⎪
⎪
⎨
+
−
⎪ I (0 ) = V − V
⎪⎩
Z0 Z0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
176
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Il coefficiente di riflessione sul piano L=0 vale
V + ZL − Z0
ΓL (0) = − =
ZL + Z0
V
• La potenza media che transita sulla linea alla generica ascissa , sotto le
ipotesi fatte, risulta costante con L e la sua espressione valutata in L=0 è:
1
1 ⎧⎪ +
∗
PL = ℜ V ⋅ I = ℜ⎨ V + V −
2
2 ⎪
⎩
{
}
(
)
⎛ V + ∗ V − ∗ ⎞⎫⎪
1
⎜
⎟
⋅
−
⎬=
⎜ Z0
⎟
Z 0 ⎠⎪ 2 ⋅ Z 0
⎝
⎭
⎡V + 2 − V − 2 ⎤
⎥⎦
⎢⎣
• I prodotti incrociati danno un contributo nullo in quanto sono l’uno il
complesso coniugato dell’altro e la loro somma fornisce un fasore
immaginario puro.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
177
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Considerando la linea con perdite, le equazioni ai fasori dei telegrafisti
divengono
⎧ V ( z ) = V + e −γ ⋅ z + V − e + γ ⋅ z
⎪
⎪
⎨
+
−
V
V
⎪I (z ) =
e −γ ⋅z −
e +γ ⋅ z
⎪⎩
Z0
Z0
dove
γ = α + jβ è un numero complesso
• α rappresenta l’attenuazione causata dalle perdite
• β costituisce il termine di propagazione
+
V = V + e − α z e − jβ z + V − e + α z e + jβ z
dove
V
V − +αz + jβz
−αz − jβz
I=
e e
−
e e
Z0
Z0
V + e −αz e − jβz = onda progressiva di tensione
dove
V − e +αz e + jβz = onda regressiva (riflessa) di tensione
+
V
e −αz e − jβz = onda progressiva di corrente
Z0
V − +αz + jβz
−
e e
= onda regressiva (riflessa) di corrente
Z0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
178
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Per calcolare l’impedenza d’ingresso si procede facendo il rapporto
tensione su corrente nel punto z=-l
⎡V ( z ) ⎤
Zi = ⎢
⎥
⎣ I ( z ) ⎦ z =−l
⎡
⎤
V − −γ ⋅l
γ ⋅l
e + +e
⎢ V + e −γ ⋅ z + V − e + γ ⋅ z ⎥
+ γ ⋅l
− −γ ⋅l
+
V
e
V
e
V
⎥
=
=⎢ +
= Z 0 + γ ⋅l
= Z0
−
−
− −γ ⋅l
V
V e −V e
⎢ V −γ ⋅ z V + γ ⋅ z ⎥
eγ ⋅l − + e −γ ⋅l
⎢Z e −Z e ⎥
V
0
⎣ 0
⎦ z =−l
eγ ⋅l + Γ0 e −γ ⋅l
= Z 0 γ ⋅l
e − Γ0 e −γ ⋅l
[
[
Z L − Z 0 −γ ⋅l
e
Z L + Z0
Z L eγ ⋅l + Z 0 eγ ⋅l + Z L e −γ ⋅l − Z 0 e −γ ⋅l
= Z0
= Z0
=
γ ⋅l
γ ⋅l
−γ ⋅l
−γ ⋅l
−
Z
Z
Z L e + Z 0e − Z L e − Z 0e
0 −γ ⋅l
eγ ⋅l − L
e
Z L + Z0
eγ ⋅l +
]
]
[
[
]
]
Z L eγ ⋅l + e −γ ⋅l eγ ⋅l + Z 0 eγ ⋅l − e −γ ⋅l
Z L [2 cosh (γ ⋅ l )] + Z 0 [2 sinh (γ ⋅ l )]
= Z0
=
=
Z
0
Z L [2 sinh (γ ⋅ l )] + Z 0 [2 cosh (γ ⋅ l )]
Z L eγ ⋅l − e −γ ⋅l eγ ⋅l + Z 0 eγ ⋅l + e −γ ⋅l
⇓
sinh (γ ⋅ l )
Z cosh (γ ⋅ l ) + Z 0 sinh (γ ⋅ l )
Z + Z 0 tanh (γ ⋅ l )
cosh (γ ⋅ l )
= Z0
= Z0 L
Zi = Z0 L
sinh (γ ⋅ l )
Z 0 cosh (γ ⋅ l ) + Z L sinh (γ ⋅ l )
Z 0 + Z L tanh (γ ⋅ l )
Z0 + Z L
cosh (γ ⋅ l )
Z L + Z0
dove
Γ0 =
Z L − Z0
è in coefficiente di riflessione sul carico Z L
Z L + Z0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
179
RICHIAMO SULLE LINEE DI TRASMISSIONE
• Per tenere conto delle perdite una linea reale si rappresenta con:
• Una resistenza in serie ad una induttanza per tenere conto dell’effetto
pelle,
• Una conduttanza in parallelo ad una capacità per tenere conto delle
perdite nel dielettrico (tgδ)
I1
L
I2
R
dell’effetto pelle,
V1
V2
C
G
•perdite nel dielettrico (tgδ)
S
⎧
⎪G = σ d d
⎨
S
⎪C = ε d
d
⎩
⇒
S
σd
σd
G
d
=
=
= tgδ
ωC ωε S ωε d
d
d
Davide Micheli
Le perdite nel dielettrico (tgδ)
aumentano con la frequenza e
bisogna tenerne conto in
quanto la potenza dissipata sul
dielettrico aumenta con il
quadrato della frequenza
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
180
Analogia Linee di Trasmissione e Propagazione libera
•
Considerando un modo T.E.M (Trasversale Elettrico, Trasversale
Magnetico) che si può assumere quando un onda EM si propaga
partendo da una sorgente relativamente lontana, allora si possono
assumere le seguenti analogie:
1.
2.
3.
4.
1
2
Tensione V con Campo Elettrico E (V=E);
Densità di Corrente J con Campo Magnetico H (J=H);
Impedenza caratteristica della linea Z0 con Impedenza d’onda η (Z0=η);
Cortocircuito = conduttore ideale
r
r ( i ) − j ⋅k ⋅ z r ( r ) + j ⋅k ⋅ z
v
+ − j ⋅β ⋅ z
− + j ⋅β ⋅ z
⎧
⎧ V (z ) = V e
Etot _ x = E e
+E e
+V e
⎪
⎪
⎪
⎪
⇒
r
⎨r
⎨r
+
−
r ( i ) − j ⋅k ⋅ z r ( r ) + j ⋅k ⋅ z
zˆ × E 1
⎪ I ( z ) = V e − j ⋅β ⋅ z − V e + j ⋅β ⋅ z ⎪ H
= zˆ × E e
−E e
tot _ y = ±
⎪⎩
⎪
Z0
Z0
η
η
⎩
[
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
181
]
Analogia Linee di Trasmissione e Propagazione libera
3
β = ω LC ⇒
L
Z0 =
C
k = ω µε
µ
⇒ η=
ε
per un dielettrico reale con perdite
jωµ
η=
σ + jωε
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
182
Materiali isolanti o dielettrici
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
183
Materiali dielettrici o isolanti: introduzione
• I materiali si possono classificare in due categorie a seconda della loro
risposta ad un campo elettrico E (costante o variabile ma con frequenza
molto bassa)
• I solidi nei quali un campo elettrico costante produce una corrente
elettrica, fatta di ioni, nel caso di conduttori ionici, o fatta di elettroni, nel
caso di conduttori elettronici, sono chiamati conduttori elettrici.
• Al contrario, gli isolanti elettrici, in cui non può circolare corrente ionica
o elettronica, sono dielettrici, in cui la unica risposta delle cariche legate
(ioni o elettroni) ad una corrente o ad un campo elettrico, e’ uno
spostamento spaziale, statico, che causa un cambiamento in un
momento di dipolo oppure induce un momento di dipolo indotto.
• Le proprietà dielettriche dei solidi sono pertanto determinate da elettroni
localizzati o cariche legate, che formano dei momenti di dipolo
elettrostatici.
• I materiali dielettrici trovano molte applicazioni soprattutto nell’ industria
elettronica, aerospaziale, delle microonde, Infatti, i materiali dielettrici
servono per la propagazione della radiazione elettromagnetica (dalle
radio frequenze al visibile), per la dispersione della luce nei mezzi ottici,
e sono usati nei congegni basati sulla piezoelettricita’
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
184
Materiali dielettrici o isolanti: introduzione
• L’ esperimento fondamentale su un dielettrico e’ la misura della
costante dielettrica ε, che si ottiene misurando la capacita’ di un
condensatore con e senza il dielettrico inserito fra le armature
• Consideriamo un condensatore isolato ad armature piane e parallele
caricato con una certa carica q. La tensione (o differenza di potenziale)
V che si misura tra le due armature sarà pari a
q = VC
• dove C è detta capacità e dipende solo dalla geometria e dal mezzo
compreso tra le due armature.
• Nel vuoto,
A
C0 = ε 0
–
d
dove A è l’area delle armature e d la loro distanza.
• Se si infila un materiale dielettrico tra le due armature, si osserva che la
tensione tra le due armature cala. Macroscopicamente, si descrive tale
fenomeno dicendo che il mezzo ha una costante dielettrica pari a εrel
quella del vuoto.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
185
Materiali dielettrici o isolanti: introduzione
• La capacità in presenza di dielettrico diventa quindi
A
C = ε r C 0 = ε 0ε r
d
• Essendo q costante, deve calare la tensione V
• Questo comportamento si spiega dicendo che il dielettrico, in presenza
di un campo elettrico (in questo caso generato dalle cariche poste sulle
due armature), si polarizza, ossia si formano dei dipoli elettrici
microscopici come illustrato schematicamente in figura.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
186
Materiali dielettrici o isolanti: Polarizzazione
• La capacità in presenza di dielettrico diventa quindi
A
C = ε r C 0 = ε 0ε r
d
• Essendo q costante, deve calare la tensione V
• Questo comportamento si spiega dicendo che il dielettrico, in presenza
di un campo elettrico (in questo caso generato dalle cariche poste sulle
due armature), si polarizza, ossia si formano dei dipoli elettrici
microscopici come illustrato schematicamente in figura.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
187
Indice di rifrazione e costante dielettrica
• Sviluppando le equazioni di Maxwell del campo elettromagnetico si può
dimostrare che la velocità cm della radiazione elettromagnetica in un
mezzo è uguale a
cm =
•
•
•
•
•
1
µr ε r µ0ε 0
Dove
εr
ε0
µr
µ0
= costante dielettrica relativa
= costante dielettrica del vuoto
= permeabilità magnetica relativa
= permeabilità magnetica del vuot
• Nel vuoto, µr =εr =1 pertanto la velocità della luce nel vuoto risulta
c =
Davide Micheli
1
µ0ε 0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
188
Indice di rifrazione e costante dielettrica
• Se ora consideriamo un materiale non magnetico allora µr=1 e quindi il
rapporto tra la velocità della luce nel vuoto e la velocità della luce nel
mezzo diventa::
µ01ε 0ε r
c
=
= εr
cm
µ0ε 0
• Il rapporto c/cn è chiamato indice di rifrazione n
• Da questa espressione ci si aspetta che sperimentalmente si possa
confermare la relazione
c
n = = εr
cn
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
189
Indice di rifrazione e costante dielettrica
• In realtà le misure mostrano una discrepanza ovvero si trova
generalmente che
n2 ≤ ε r
• Ad esempio la costante dielettrica εr del NaCl misurata con campi
variabili di bassa frequenza è circa 5.9 mentre si trova che n2 è circa 2.5
• L’H2O è il caso più estremo, la costante dielettrica εr misurata con campi
variabili di bassa frequenza è circa 81 mentre si trova che n2 è circa 1,75
• Solo materiali come il diamante, dove l’unico meccanismo di
polarizzazione è quello elettronico, mostrano un ottimo accordo di
εr=5.68 ed n2=5.66
• la ragione di queste discrepanze è che l’indice di rifrazione è misurato a
frequenze ottiche (≈1015 Hz) mentre la costante dielettrica è misurata a
frequenze molto più basse.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
190
Espressione complessa di
ε e dipendenza in freq.
• Convenzionalmente si parla di costante dielettrica (o permittività) per
basse frequenze dello spettro elettromagnetico e si parla di indice di
rifrazione per la luce.
• Se si misura ε in funzione della frequenza, si trova che esso cala, ma
non in modo graduale.
n2
Davide Micheli
• L’andamento
mostra
una serie di brusche
variazioni (cadute), in
corrispondenza
di
precise
frequenze,
finché non si arriva al
valore di n2, idealmente
pari a 1
• Associata a ciascuna di
queste cadute c’è una
regione di dissipazione
dell’energia o perdita
dielettrica
(dielectric
Loss)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
191
Espressione complessa di
ε e dipendenza in freq.
• La figura mostra due componenti della costante dielettrica: ε’ e ε’’
• queste due quantità sono la parte reale e la parte immaginaria della
costante dielettrica che nella sua forma più generale è un numero
complesso:
ε~ = ε '+ jε ' '
• L’andamento generale delle componenti reale ed immaginaria di ε è
sempre quello mostrato in figura:
–
–
ε’ varia rapidamente in prossimità di certe frequenze;
ε’’ mostra per le stesse frequenze dei picchi
• Le diverse sorgenti di polarizzazione costituiscono alla costante
dielettrica in diverse regioni di frequenza, a seconda che siano gli
elettroni o gli atomi (ioni) responsabili.
• La massa inerziale più piccola degli elettroni implica che il meccanismo
elettronico domina alle frequenze elevate.
• Le polarizzazioni legate allo spostamento di atomi o ioni contribuiscono
solo alle frequenze più basse.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
192
Espressione complessa di
ε e dipendenza in freq.
• Si sono già anticipate almeno intuitivamente le ragioni della diminuzione
della parte reale di ε, ma come si più invece spiegare la presenza di
picchi nella parte immaginaria ?
• Interpretazione intuitiva: le molecole hanno frequenze naturali a causa
dei legami nel cristallo e trasferiranno il massimo dell’energia da un
onda elettromagnetica che abbia la stessa frequenza.
• Queste due caratteristiche della costante dielettrica, ovvero
–
–
La dipendenza dalla frequenza del campo elettrico applicato
Il fatto che a certe frequenze l’energia può essere dissipata entro il
dielettrico,
Costituiscono gli aspetti più importanti ed interessanti nella teoria dei
materiali dielettrici.
• Il rapido cambiamento nella parte reale della costante dielettrica che si
ha con l’aumentare della frequenza del campo elettrico applicato,
suggerisce che in prossimità di ciascuna delle frequenze caratteristiche,
uno dei meccanismi di polarizzazione si spegne.
• Questo accade perché la polarizzazione non riesce a seguire la
variazione di campo elettrico.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
193
Espressione complessa di
ε e dipendenza in freq.
• Esistono due possibili meccanismi che originano il fenomeno della
dipendenza della costante dielettrica dalla frequenza:
–
–
Assorbimento di risonanza
Rilassamento dei dipoli.
• Ogni volta che esiste una configurazione di equilibrio della specie
polarizzabile (cioè la polarizzazione riesce a seguire il campo elettrico
applicato), allora ha luogo l’assorbimento di risonanza.
• L’unica caso in cui questo meccanismo non è operativo è quello della
orientazione dei dipoli, perché questo coinvolge dei dipoli che sono
liberi di ruotare e che quindi non hanno una configurazione di equilibrio.
• In questo caso la dinamica orientazionale è governata da equazioni di
rilassamento ed il meccanismo che opera è il rilassamento dei dipoli.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
194
Assorbimento di risonanza
• Ogni tipo di dipolo indotto può essere pensato come costituito da due
cariche di segno opposto che sono legate tra loro da una forza elastica.
• Questo sistema avrà una frequenza angolare di oscillazione naturale
pari ad ω0.
• Se il sistema è sottoposto ad un campo elettrico alternato con frequenza
ω, allora il sistema non sarà in grado di seguire questo campo se ω > ω0.
• Questo problema è l’analogo del problema di meccanica classica di una
vibrazione forzata di un semplice sistema armonico, e la quanto
meccanica non cambia essenzialmente il risultato. Per tale motivo si
può continuare a seguire la trattazione semi-clcassica senza timore di
commettere errori gravi.
• Il problema si può esprimere in una forma matematica semplice che
porta il nome di Equazione di Lorentz per un Oscillatore Forzato
Smorzato (Driven dumped Oscillator).
m&x& + mbx& + kx = qE
m⋅a
Termine dissipativo
Davide Micheli
Termine forzante
Termine Armonico
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
195
Assorbimento di risonanza
• Dove: m è la massa della specie oscillante di carica q, e x è la
separazione tra le cariche associata con la polarizzazione.
• Nell’equazione è stato anche incluso un termine di spegnimento
(dissipativo), con coefficiente b che è proporzionale alla velocità della
particella. Questo termine è necessario in quanto affinché si abbia
dissipazione di energia del campo elettromagnetico (ovvero
assorbimento di energia nel materiale dielettrico), occorre che ci sia un
meccanismo di interazione.
• k è la costante di forza che caratterizza la risposta del sistema ad un
campo oscillante E=E0exp(jωt).
• Considerando come esempio il moto di un elettrone di massa m e carica
–e (ovvero specializzandosi nel casi di polarizzazione elettronica) si può
scrivere l’equazione di Lorentz come segue:
d 2x
dx
2
m 2 + mb + mω x = −eE0 exp(− jωt )
dt
dt
m⋅a
Termine dissipativo
Termine Armonico
Davide Micheli
Termine forzante
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
196
Assorbimento di risonanza
• La soluzione stazionaria dell’equazione precedente, dimenticando effetti
transienti, è:
x = x0 exp(− jωt )
− eE0
x0 =
m ω02 − ω 2 − jbω
{(
)
}
• Essendo x0 complesso risulta conveniente separarlo nelle componenti
reale ed immaginaria, allora moltiplicando il numeratore ed il
denominatore per il numero complesso coniugato del denominatore:
− eE0
x0 =
m
(
)
⎧⎪
⎫⎪
ω02 − ω 2
jbω
+
⎨ 2
⎬
2 2
2 2
2
2 2
2 2
⎪⎩ ω0 − ω + b ω
ω0 − ω + b ω ⎪⎭
(
)
Davide Micheli
(
)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
197
Assorbimento di risonanza
• Ora lo spostamento, x, delle cariche, è proporzionale alla polarizzabilità
α, e quindi varierà allo stesso modo:
p = qx0 = αE0
(
)
⎫⎪
qx0 e ⎧⎪
ω02 − ω 2
jbω
⇒ α=
= ⎨
+
⎬
2
2
2
2
2
2
2
2
2
2
E0 m ⎪⎩ ω0 − ω + b ω
ω0 − ω + b ω ⎪⎭
(
)
(
)
• La parte immaginaria della polarizzabilità ha un picco di forma
Lorentziano in corrispondenza della frequenza di risonanza ω0,
corrispondente all’assorbimento risonante dell’energia.
• La larghezza del picco cresce al crescere del coefficiente di
spegnimento b.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
198
Assorbimento di risonanza
• La parte reale di x0 mostra una discontinuità in corrispondenza della
frequenza di risonanza ω0.
• Infatti ha un valore molto elevato poco prima della risonanza e diventa
molto basse poco dopo la risonanza.
• Per frequenze lontane da ω0, la parte reale cambia ancora e mostra un
massimo ed un minimo ai fianchi della risonanza.
α’
α’’
• Per inciso la trattazione
quanto meccanica porta
ad una espressione della
polarizzabilità analoga a
quella vista ma dove
compaiono le transizioni
fra stati permessi del
sistema.
• (vedi espressioni usate
per
la
spettroscopia
Raman)
α’’
α’
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
199
Assorbimento di risonanza
• Gli andamenti appena descritti sono applicabili anche alla costante
dielettrica perché se ci si dimentica degli effetti del campo locale, allora
questa è proporzionale alla polarizzabilità: ε ∝ α
• se inoltre si tiene conto anche di diversi meccanismi che generano
polarizzazione dovuti ad ni specie per unità di volume allora, sommando
tutti questi meccanismi si può scrivere:
(
)
⎫⎪
ω02,i − ω 2
ni q 2 ⎧⎪
ε ' = ε (∞ ) + ∑
⎨ 2
2
2 2⎬
2
i ε 0 m ⎪ ω 0 ,i − ω
+ bi ω ⎪⎭
⎩
(
)
⎫⎪
ni q 2 ⎧⎪
bi ω
ε ''= ∑
⎨ 2
2
2 2⎬
2
i ε 0 m ⎪ ω 0 ,i − ω
+ bi ω ⎪⎭
⎩
(
)
• La sommatoria ci dice
che
per
materiali
complessi, in cui le
molecole possono avere
diverse frequenze di
risonanza, la dipendenza
di ε dalla frequenza può
essere molto complicata.
• Pertanto si è dimostrato che la espressione più completa dalla costante
dielettrica è
ε~ = ε '+ jε ' '
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
200
Assorbimento di risonanza
• Per comprendere l’importanza del termine Lorentziano, ovvero la parte
immaginaria della costante dielettrica complessa, si può dimostrare che
esso da luogo alla dissipazione di energia nel dielettrico.
• Infatti si può dimostrare che la potenza dissipata è data da:
1
ε 0ε ' ' ωE02
2
Ovvero dipende solo
parte
immaginaria
costante dielettrica
dalla
della
• Nel disegno ε1 sta per ε’ ed
ε2 sta per ε’’
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
201
Rilassamento dei dipoli
• Rilassamento dielettrico: Genericamente il termine “rilassamento”
definisce un fenomeno per mezzo del quale un sistema perturbato tende
all’equilibrio. Per un dielettrico, si definisce RILASSAMENTO
DIELETTRICO il graduale orientamento di tutti i dipoli del materiale, a
seguito della repentina applicazione di un campo elettrico (continuo o
alternato). Tale orientamento avviene durante un determinato intervallo
temporale, al termine del quale il materiale dielettrico manifesta la
massima polarizzazione e la massima permittività dielettrica.
• Tempo di rilassamento dielettrico: è la costante di tempo caratteristica τ
che quantifica il ritardo con cui la polarizzazione dielettrica P o lo
spostamento dielettrico D seguono il campo elettrico applicato.
• Osservazione: il rilassamento dielettrico può avvenire mediante
differenti “riarrangiamenti” molecolari, ciascuno caratterizzato da una
propria costante di tempo caratteristica.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
202
Rilassamento dei dipoli
• si supponga di applicare ad un dielettrico un campo elettrico statico
(costante) E=E0 in un certo istante t=0, ossia si supponga di applicare
una funzione campo elettrico E(t) a gradino:
E (t ) = E0u (t ) con
⎧0 per t < 0
u (t ) = ⎨
⎩1 per t ≥ 0
• A seguito del rilassamento dielettrico la polarizzazione del materiale
aumenterà gradatamente da un valore P∞ (polarizzazione istantanea),
posseduta dal materiale all’istante t=0, ad un valore di regime PS
(polarizzazione statica).
• Conseguentemente, la parte reale della costante dielettrica relativa
ε’r(ω), passerà da un valore ε'r,∞ istantaneo (in t=0) ad un valore ε’r,s
statico (per t→∞).
• Risulta inoltre ε'r,∞ < ε’r,s in quanto il valore istantaneo è legato solo ad
effetti di polarizzazione per deformazione e non ad effetti di
orientamento, essendo questi ultimi intrinsecamente più lenti.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
203
Rilassamento dei dipoli
E(t)
E0
t
PS
P(t)
P∞
t
ε’r s
Evoluzione temporale
qualitativa della
polarizzazione e del
valore della permittività
dielettrica, per un
dielettrico con perdite
per rilassamento
dielettrico, sollecitato da
un gradino di campo
elettrico.
ε’r ∞
1
t
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
204
Rilassamento dei dipoli
• La dipendenza dalla frequenza della costante dielettrica ε per il
meccanismo di orientazione dei dipoli, può essere calcolata con il
modello del rilassamento dipolare di Debye.
• L’applicazione improvvisa di un campo elettrico, causa una
polarizzazione P che è istantanea sulla scala dei tempi della rotazione
dipolare.
• La costante dielettrica associata è ε(∞) cioè corrispondente a frequenze
di campo elettrico infinitamente grandi (sulla scala delle frequenze
rotazionali.
P(∞ ) = ε 0 [ε (∞ ) − 1]E
• il rilassamento dei dipoli a questo punto causa un aumento della
polarizzazione con una componente dipendente dal tempo P’(t) finché
non si raggiunge il valore statico PS’ ( ε(0) o εs è il valore a campo
statico della costante dielettrica.)
PS = ε 0 [ε (0) − 1]E dove si ha : PS = P∞ + P' (t = ∞ )
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
205
Rilassamento dei dipoli
• La
crescita
istantanea
di
polarizzazione al tempo t=0 è
dovuta meccanismi elettronici e
ionici.
• La
polarizzazione
per
orientamento causa una crescita
lenta al valore statico PS.
• L’equazione di rilassamento di Debye è:
• Dove la polarizzazione totale al tempo t è:
dP ' PS − P(t )
=
dt
τD
P(t ) = P∞ + P' (t )
(1)
• τD è il tempo di rilassamento di Debye che si assume essere
indipendente dal tempo
• La dipendenza temporale di P si trova integrando l’equazione (1) e
tenendo presente l’espressione di P appena vista.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
206
Rilassamento dei dipoli
dP' PS − P(t ) PS − P∞ − P' (t )
=
=
dt
τD
τD
t
dP'
dt
=
⇒
PS − P∞ − P' (t ) τ D
if
x = PS − P∞ − P' (t )
d (ln ( x ))
dt
∫0 − dP' = ∫0 τ D
t
(1)
t
dP'
dt
=
∫0 PS − P∞ − P' (t ) ∫0 τ D
then
t
−1
d (ln ( x )) 1 dx
=
=
dP'
x dP' PS − P∞ − P' (t )
[- ln(PS − P∞ − P' (t ))]
t
0
⇒
- ln (PS − P∞ − P' (t )) + ln (PS − P∞ − P' (0 )) =
⎛ PS − P∞ − P' (t ) ⎞
t
⎟⎟ = −
ln⎜⎜
τD
⎝ PS − P∞ − P' (0) ⎠
PS − P∞ − P' (t ) = (PS − P∞ )e
t
τD
−
t
⎡ t ⎤
=⎢ ⎥
⎣τ D ⎦ 0
0
τD
dove P' (0 ) = 0
−
t
τD
Davide Micheli
⇒
t
−
⎛
P' (t ) = (PS − P∞ )⎜1 − e τ D
⎜
⎝
⎞
⎟
⎟
⎠
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
207
Rilassamento dei dipoli
t
−
⎛
P' (t ) = (PS − P∞ )⎜1 − e τ D
⎜
⎝
⎞
⎟
⎟
⎠
• Questa relazione mostra la dipendenza
temporale dalla polarizzazione, che cresce
da P∞ a PS
• Alternativamente si può dire che la polarizzazione decresce
esponenzialmente nel tempo da Ps a P∞ se il campo elettrico viene
rimosso.
• Dalla espressione della polarizzazione funzione del campo elettrico si
può ottenere la dipendenza temporale della costante dielettrica
t
−
⎛
⎞
τ
P' (t ) = (PS − P∞ )⎜1 − e D ⎟ = χ (t )ε 0 E0 exp(− jωt ) =
⎜
⎟
⎝
⎠
= (ε~rel (t ) − 1)ε 0 E0 exp(− jωt )
• εrel, è solo la componente dovuta alla orientazione dei dipoli εrel= ε∞ +εrel(t)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
208
Rilassamento dei dipoli
• La relazione funzione del tempo appenea ricavata può essere
trasformata in una relazione funzione della frequenza facendo uso della
trasformata di Fourier
∞
f (ω ) = K ∫ F (t )e jωt dt
0
• Con questa operazione si giunge alla espressione finale della costante
dielettrica complessiva che è ancora una volta espressa come un
numero complesso:
ε (0) − ε (∞ )
~
ε rel (ω ) = ε (∞ ) +
= ε '+ jε ' '
1 − jωτ D
• La parte reale ed immaginaria si ottiene moltiplicando e dividendo per il
complesso coniugato del denominatore:
ε (0) − ε (∞ )
ε ' (ω ) = ε (∞ ) +
1 + ω 2τ D2
parte reale
Davide Micheli
(
ε (0) − ε (∞ ))ωτ D
ε ' ' (ω ) =
2 2
1+ ω τ D
parte immaginaria
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
209
Rilassamento dei dipoli
• L’andamento di ε’ ed ε’’ in funzione della pulsazione ωτD è mostrata ni
grafici seguenti:
parte reale
ε (0) − ε (∞ )
ε ' (ω ) = ε (∞ ) +
1 + ω 2τ D2
ε’
parte immaginaria
(
ε (0) − ε (∞ ))ωτ D
ε ' ' (ω ) =
2 2
ε’’
1+ ω τ D
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
210
Rilassamento dei dipoli
• È da notare in particolare il
diverso andamento di ε’ rispetto
al caso dell’oscillatore smorzato
descritto in precedenza.
• In particolare si nota che
mancano il massimo e il minimo
ai fianchi della risonanza,
caratteristica che è verificata
sperimentalmente.
• La curva di ε’’, mostra un valore
centrato ad ω=1/τD, e in generale
è molto più allargato rispetto al
caso di assorbimento per
risonanza.
Davide Micheli
ε’
parte reale
ln(ωτ)
ε’’
parte immaginaria
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
ln(ωτ)
211
Costante dielettrica complessa
• Possiamo concludere osservando che i fenomeni che abbiamo appena
discusso si applicano al materiale dielettrico di piu’ grande importanza
per la nostra esistenza: l’ atmosfera terrestre
• Dello spettro elettro-magnetico quasi completo emesso dal sole, solo
poca radiazione raggiunge la terra
• Frequenze al di sotto di 108Hz sono assorbite o riflesse dalla ionosfera
• Le frequenze nell’ intervallo 1010-1014 Hz spariscono per assorbimento di
risonanza da parte di molecole come H2O, CO2, O2, N2.
• Al di sopra di 1015 Hz c’e’ un elevato scattering da parte delle molecole e
particelle di polvere
• La regione del visibile (1014-1015 Hz) e’ stata di fondamentale importanza
per l’ evoluzione della vita sulla terra
• Potremmo chiederci come sarebbe stata la vita sulla terra se, con un po’
piu’ di polveri in giro, avessimo potuto utilizzare solo la regione 108-1010
Hz della radiazione elettro-magnetica, per la nostra visione.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
212
Rigidità dielettrica
• Un’altra grandezza importante nell’uso corretto dei dielettrici è la
cosiddetta rigidità dielettrica.
• Questa corrisponde al valore massimo del campo elettrico che si può
applicare al materiale, oltre il quale si innesca una scarica distruttiva.
• Se il campo E è sufficientemente intenso, è in grado di liberare le
cariche “legate” le quali possono ionizzare atomi producendo altre
cariche con un effetto valanga devastante.
• Anche la rigidità dielettrica dipende dalla natura del materiale e si può
trovare tabulata come nella tabella seguente:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
213
DIELETTRICI CON PERDITE PER
RILASSAMENTO DIELETTRICO:
applicazione di un campo
elettrico alternato
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
214
Effetto applicazione campo elettrico alternato
• Applicando ad un dielettrico con perdite un campo elettrico E avente
una variazione temporale di tipo sinusoidale:
E = E0 cos(ωt )
• L’orientamento dei dipoli subirà un ritardo (rispetto ad E) tanto
maggiore quanto maggiore sarà la pulsazione ω (ω=2πf, f=frequenza),
che si manifesterà con uno sfasamento δ(ω) dello spostamento
dielettrico D rispetto ad E:
D = D0 cos(ωt − δ (ω ))
• Introducendo il concetto di fasore, data una grandezza sinusoidale
x(t ) = X 0 cos(ωt + Φ )
• Si definisce fasore rotante associato ad x(t) la quantità:
X& (ω , t ) = X 0 e j (ωt + Φ ) = X 0 cos(ωt + Φ ) + jX 0 sin (ωt + Φ ) dove j2 = −1
pertanto si ha : x(t ) = Re{X& (ω , t )}
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
215
Effetto applicazione campo elettrico alternato
• Pertanto i fasori associati alle grandezze Campo elettrico E e
Spostamento dielettrico D sono:
E& (ω , t ) = E0 e j (ωt ) ⇒ E = Re{E& (ω , t )}
D& (ω , t ) = D0 e j (ωt −δ (ω )) ⇒ D = Re{D& (ω , t )}
• Come è stato visto, la costante dielettrica o permittività dielettrica
relativa complessa di un dielettrico con perdite per rilassamento del
dielettrico, sottoposto ad un campo elettrico tempo-variabile è:
ε~r = ε r' (ω ) − jε r'' (ω )
• Il fasore del vettore spostamento elettrico D del dielettrico è:
~
&
(
)
D ω , t = ε 0ε r E& (ω , t )
• Questo fasore lo possiamo riscrivere tenendo conto delle relazioni viste:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
216
Effetto applicazione campo elettrico alternato
D& (ω , t ) = ε ε~ E& (ω , t ) = ε ε ' (ω ) − jε '' (ω ) E& (ω , t )
0 r
0
(
r
(
r
)
)
D0 e j (ωt −δ (ω )) = ε 0ε~r E0 e j (ωt ) = ε 0 ε r' (ω ) − jε r'' (ω ) E0 e j (ωt )
(
)
D0 e j (ωt )e − j (δ (ω )) = ε 0 ε r' (ω ) − jε r'' (ω ) E0 e j (ωt )
(
)
D0 e − j (δ (ω )) = ε 0 ε r' (ω ) − jε r'' (ω ) E0
D0 cos(δ (ω )) − jD0 sin (δ (ω )) = ε 0ε r' (ω )E0 − jε 0ε r'' (ω )E0
• Separando la parte reale da quella immaginaria abbiamo:
D0 cos(δ (ω ))
⎧
ε r (ω ) =
'
⎪
⎫⎪ ⎪
D0 cos(δ (ω )) = ε 0ε r (ω )E0
ε 0 E0
⎬⇒ ⎨
''
− jD0 sin (δ (ω )) = − jε 0ε r (ω )E0 ⎪⎭ ⎪ '' ( ) D0 sin (δ (ω ))
εr ω =
⎪⎩
ε 0 E0
• Come già detto
ε&&r
rappresenta il fattore di perdita del dielettrico
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
217
Effetto applicazione campo elettrico alternato
• Osservazioni:
δ (0) = 0
D0
⎧ '
(
)
=
ε
ω
⎪ r
ε 0 E0
⇒ ⎨
⎪ε '' (ω ) = 0
⎩ r
se il dielettrico è privo di perdite si ha : δ (ω ) = 0
D0
⎧ '
⎪ε r (ω ) = ε E
⇒ ⎨
0 0
⎪ε '' (ω ) = 0
⎩ r
per ω = 0 campo statico,
• Per confrontare le perdite di dielettrici differenti si usa la quantità tg(δ):
ε r'' (ω )
tg (δ (ω )) = '
ε r (ω )
• Per il fattore di qualità del dielettrico si usa invece la espressione Q(ω):
Q(ω ) =
Davide Micheli
1
tg (δ (ω ))
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
218
Effetto applicazione campo elettrico alternato
• Significato fisico di:
ε r' (ω ), ε r'' (ω ),
tg (δ (ω ))
• si supponga di applicare una tensione alternata ad un condensatore
planare con elettrodi aventi area A e distanza z
V = V0 cos(ωt )
Definizione:
Capacità complessa del
Condensatore planare
sollecitato in alternata
~
C (ω ) = C0ε~ (ω )
z
V V0 cos(ωt )
E= =
z
z
A
dove : C0 = ε 0
z
Condensatore planare
sollecitato in alternata
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
219
Effetto applicazione campo elettrico alternato
• Utilizzando nuovamente i fasori si ottiene:
V& (ω , t ) = V0 e jω
& (ω , t )
V
~
&I (ω , t ) =
= jωC (ω )V& (ω , t ) = jωC0ε~r (ω )V& (ω , t )
1 ~
jωC (ω )
= jωC ε ' (ω) − jε '' (ω) V& (ω , t ) = ωC ε '' (ω) + jε ' (ω) V& (ω , t ) =
0
(
r
r
)
0
(
= ωC0ε r'' (ω)V& (ω , t ) + jωC0ε r' (ω)V& (ω , t )
V = V0 cos(ωt )
R
I
IR
1
Y = + j ωC
R
C
IC
Davide Micheli
r
r
)
• Tale espressione è compatibile
con il seguente CIRCUITO
ELETTRICO
EQUIVALENTE:
un dielettrico con perdite per
rilassamento
dielettrico
è
elettricamente equivalente al
parallelo tra un resistore ed un
condensatore ideali
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
220
Effetto applicazione campo elettrico alternato
• Le correnti espresse mediante i fasori rotanti sono:
V = V0 cos(ωt )
R
I
IR
C
I&(ω , t ) = I&R (ω , t ) + I&C (ω , t )
⎧&
V& (ω , t )
⎪ I R (ω , t ) =
dove : ⎨
R
⎪ I& (ω , t ) = jωCV& (ω , t )
⎩ C
IC
• Confrontando tali espressioni con le espressioni della parte reale ed
immaginaria del fasore della corrente trovato in precedenza si ha:
I&(ω , t ) = I&R (ω , t ) + I&C (ω , t ) =
& (ω , t )
V
= ωC ε (ω)V& (ω , t ) + jωC ε (ω)V& (ω , t ) =
+ jωCV& (ω , t )
R
& (ω , t )
V
'
'
⇒ I&R (ω , t ) = ωC0ε r (ω)V& (ω , t ) =
R
⇒ I&C (ω , t ) = ωC0ε r' (ω )V& (ω , t ) = ωCV& (ω , t )
''
0 r
'
0 r
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
221
Effetto applicazione campo elettrico alternato
• Le correnti espresse mediante i fasori rotanti sono:
& (ω , t )
1
V
''
&
⇒ ωC ε (ω)V (ω , t ) =
⇒ ωC0ε r (ω) =
R
R
⇒ ωC0ε r' (ω)V& (ω , t ) = ωCV& (ω , t ) ⇒ C0ε r' (ω) = C
''
0 r
⇓
1
• R(ω) =
ωC0 ε''r (ω)
⇒
• C (ω) = C ε (ω)
⇒
'
0 r
1
ε (ω) =
⇒ Resistenza Equivalente
ωC0 R(ω)
''
r
C (ω)
ε (ω) =
C0
'
r
⇒ Capacità Equivalente
• ε'r (ω) > 1 per ogni dielettrico diverso dal vuoto, per il vuoto vale 1
1 z ε0
lunghezza
• σ ac (ω) = ρ (ω)
=
= ωε 0ε r'' (ω)
sezione
R(ω) A C0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
222
Effetto applicazione campo elettrico alternato
• Osservazioni
• La componente IR dissipa energia nel dielettrico,
• La componente IC del dielettrico accumula energia nel dielettrico,
1
1
energia dissipata/ciclo
ε''r (ω) ωC0 R(ω)
tg (δ (ω)) = '
=
=
=
C (ω)
εr (ω)
ωC (ω)R(ω) energia immagazzinata/ciclo
C0
• All’aumentare del tg(δ(ω)), aumentano pertanto le perdite di energia
dissipata nel dielettrico,
• È possibile schematizzare il circuito equivalente di un dielettrico anche
con un resistore ed una condensatore in serie e determinare poi ε’ ed ε’’
in funzione della resistenza e capacità in serie.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
223
Dielettrici con perdite ohmiche
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
224
Dielettrici con perdite ohmiche
• In un dielettrico eventuali cariche libere possono essere accelerate dal
campo elettrico applicato per essere trasportate all’interno del
dielettrico, dando luogo ad una conducibilità in regime continuo (σdc),
così chiamata perché si manifesta anche in continua (dc), e non soltanto
in regime sinusoidale (ac), a differenza di quanto accade per la
conducibilità derivante da perdite per rilassamento dielettrico (σac(ω) ).
• Ne consegue il seguente CIRCUITO ELETTRICO EQUIVALENTE: un
dielettrico con perdite puramente ohmiche è elettricamente equivalente
al parallelo tra un condensatore e un resistore avente resistenza (R0)
indipendente dalla frequenza:
R0
=
Davide Micheli
C
σ dc
ε0
1 Z
=
=
R0 A R0C0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
225
Dielettrici con perdite sia per
rilassamento dielettrico sia ohmiche
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
226
Dielettrici con perdite ohmiche
• Nel
caso
più
generale
un
dielettrico
può
presentare
contemporaneamente perdite per rilassamento dielettrico e perdite
ohmiche.
• Assumendo
un
circuito
elettrico
equivalente
di
tipo
resistore/condensatore in parallelo, il resistore deve essere ritenuto a
sua volta come il parallelo tra un resistore R, derivante dalla
schematizzazione delle perdite per puro rilassamento dielettrico, ed un
resistore R0, derivante dalla schematizzazione delle perdite puramente
ohmiche:
V = V0 cos(ωt )
R// (ω ) = R(ω ) // R0 =
R
I
IR
C
IC
1
1
1
+
R(ω ) R0
R0
IR0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
227
Dielettrici con perdite ohmiche
• Per un tale dielettrico si definisce:
• Costante (o permeabilità o permittività) dielettrica relativa complessa
efficace di un dielettrico con perdite sia per rilassamento dielettrico sia
ohmiche:
ε~r ,eff (ω ) = ε r' ,eff (ω ) − jε r'',eff (ω ) procedendo come prima si ottiene :
⎧ ''
σ dc
1
1 ⎛ 1
1 ⎞
''
''
⎜⎜
=
+ ⎟⎟ ⇒ εr,eff (ω) = εr (ω) +
⎪ε r ,eff (ω ) =
ωR// (ω )C0 ωC0 ⎝ R(ω ) R0 ⎠
ωε 0
⎪
⎨
'
'
⎪ε ' (ω ) = C
(
)
ε
ω
ε
⇒
=
r,eff
r (ω )
⎪ r ,eff
C0
⎩
⇓
⎛ ''
σ dc ⎞
⎜
⎟⎟
r ,eff (ω ) = ε (ω ) − j ⎜ ε r (ω ) +
ωε 0 ⎠
⎝
Osservazione : ConducibilitàEquivalente
ε~
'
r
z
1 ε0
=
= ωε 0ε r'',eff (ω ) = ωε 0ε r'' (ω ) + σ dc
σ ac (ω) =
R// (ω ) A R// (ω ) C0
1
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
228
Permittività dielettrica complessa di
un materiale composito costituito da
due fasi dielettriche:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
229
Permittività dielettrica complessa di un materiale
composito costituito da due fasi dielettriche:
Esistono
varie
relazioni
(derivanti da modelli diversi o
empiriche) che quantificano la
permittività complessa εr* di
una mescola ottenuta da una
fase dielettrica di permittività
dispersa εr2* con una frazione
volumetrica v2, in una matrice
dielettrica di permittività εr1* .
Esempi:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
230
Permittività dielettrica complessa di un materiale
composito costituito da due fasi dielettriche:
Esempi di materiali
dielettrico/dielettrico:
che
presentano
interfacce
di
discontinuità
Dielettrico con crepe e vuoti:
può essere schematizzato in prima approssimazione come un materiale
eterogeneo costituito da inclusioni dielettriche di permittività ε’r2=1 in una
matrice dielettrica di permittività ε’r2>1 . Dalle equazioni precedenti si ha
che la permittività di un materiale con crepe e vuoti risulta inferiore a
quella del materiale puro e omogeneo.
Dielettrico semicristallino:
può essere schematizzato tenendo conto della presenza di inclusioni
cristalline in una matrice amorfa.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
231
Permittività dielettrica complessa di un
materiale composito dielettrico contenente
sfere parzialmente conduttrici
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
232
Dielettrico contenente sfere parzialmente conduttrici
• Modello di Wagner:
supponendo che il dielettrico contenga sfere parzialmente conduttrici
(ε’r2, σdc2), con una frazione di volume v2, immerse nella matrice dielettrica
(ε’r1) con conducibilità trascurabile (σdc1<< σdc2), il modello di Wagner
prevede la seguente espressione della permittività complessa relativa del
composto:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
233
Dielettrico contenente sfere parzialmente conduttrici
• Modello di Wagner:
Da tali espressioni risulta che il composito mostra un rilassamento
dielettrico con forma indistinguibile da quello dovuto all’orientamento
dipolare. Può accadere pertanto che un dielettrico che non possegga un
accentuato rilassamento dipolare, in realtà possa presentare ugualmente
un “effetto di rilassamento” dovuto, però, a fenomeni di polarizzazione
interfacciale.
Concludendo, possiamo dire che un materiale composito che presenti al
suo interno interfacce tra due materiali dielettrici e/o conduttori presenta
in prossimità delle interfacce accumuli di carica di polarizzazione ed
eventualmente anche di carica libera.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
234
Dielettrico contenente sfere parzialmente conduttrici
• Modello di Wagner:
Le cariche di polarizzazione determinano una variazione (rispetto al
materiale puro) della polarizzazione ed una conseguente variazione della
costante dielettrica. In particolare si ha:
Per interfacce dielettrico/dielettrico:
in ragione della dielettricità delle inclusioni, la costante dielettrica del
composito può risultare diminuita (inclusioni di aria) o accresciuta
(inclusioni altamente dielettriche) rispetto a quella della matrice. Esistono
vari modelli predittivi per la costante risultante.
Per interfacce dielettrico/conduttore:
la costante dielettrica del composito risulterà tendenzialmente
accresciuta, secondo il modello di Wagner. Si noti (dalle equazioni del
modello di Wagner) che la presenza di inclusioni conduttrici accresce sia
εr’ che εr’’ : ciò significa che ad un auspicabile (in molte applicazioni)
aumento dell’energia immagazzinata, corrisponde uno svantaggioso
aumento dell’energia persa per dissipazione.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
235
Metodi di misura di proprietà dielettriche
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
236
Metodi di misura di proprietà dielettriche
Ai fini della misura della parte reale e della parte immaginaria della
costante dielettrica complessa di un dielettrico, esistono i due seguenti
metodi:
• metodi a circuito a parametri concentrati;
• metodi a circuito a parametri distribuiti.
Metodi di misura a circuito a parametri concentrati:
Tali tipi di metodi sono utilizzati sempre a “bassa” frequenza
(da 10-4 a 106 Hz circa) e consistono nella determinazione del circuito
elettrico a parametri concentrati equivalente al campione ad una
determinata frequenza. Tipicamente il campione è schematizzato con un
circuito equivalente resistore/condensatore in parallelo o in serie e,
misurando i parametri incogniti costituiti dalla resistenza Rx e dalla
capacità Cx, si risale ai valori di εr,eff’ e di εr,eff’’ , ossia alle componenti
reale ed immaginaria della permittività efficace:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
237
Metodi di misura di proprietà dielettriche
Metodi di misura a circuito a parametri concentrati:
Uno dei metodi di misura a parametri concentrati tra i più usati è il
Metodo a ponte
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
238
Metodi di misura di proprietà dielettriche
2. Metodi di misura a circuito a parametri distribuiti:
Al crescere della frequenza, la lunghezza d’onda elettromagnetica del
campo applicato diminuisce, divenendo sempre più confrontabile con le
dimensioni del campione. Risulta quindi necessario adottare una
schematizzazione del dielettrico a parametri distribuiti. Uno dei metodi a
parametri distribuiti, tipicamente usato nell’intervallo delle microonde, è il
seguente:
• Metodo a linea di trasmissione (o a trasmissione d’onda):
in tale metodo il campione costituisce il mezzo di propagazione di
un’onda elettromagnetica confinata in una linea di trasmissione coassiale
(costituita da un conduttore centrale incluso in un tubo cavo conduttore),
o, a frequenze maggiori, in una semplice guida d’onda (tubo cavo
conduttore di sezione rettangolare o circolare.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
239
Metodi di misura di proprietà dielettriche
2. Metodi di misura a circuito a parametri distribuiti:
• Metodo a linea di trasmissione (o a trasmissione d’onda):
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
240
Metodi di misura di proprietà dielettriche
2. Metodi di misura a circuito a parametri distribuiti:
• Metodo a linea di trasmissione (o a trasmissione d’onda):
• Fattore di propagazione di un’onda elettromagnetica in un materiale
dielettrico (non magnetico):
• è il seguente numero complesso, funzione della permittività
complessa del materiale:
γ~ (ω ) = jω ε~r (ω )ε 0 µ 0 = jω ε 0 µ 0 ε~r (ω ) =
= γ 0 (ω ) ε~r (ω ) = jβ 0 (ω ) ε~r (ω ) = α (ω ) + jβ (ω )
dove :
β (ω ) =
2π
λ (ω )
β 0 (ω ) =
2π
λ0 (ω )
= ω ε 0 µ0 =
ω
c
c = velocità della luce
α (ω ) = attenuazione dell' onda nel mezzo (nel vuoto α = 0)
λ (ω ) = lunghezza d' onda nel mezzo
λ0 (ω ) = lunghezza d' onda nel vuoto
µ 0 = permeabilità magnetica del vuoto
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
241
Metodi di misura di proprietà dielettriche
2. Metodi di misura a circuito a parametri distribuiti:
• Metodo a linea di trasmissione (o a trasmissione d’onda):
• Equazioni dei fasori del campo elettrico e magnetico:
• per un’onda elettromagnetica piana, che si propaga in direzione x in
un mezzo uniforme e infinito, valgono le seguenti espressioni:
jωt −γ
E& = E0 e
jωt −γ
&
H =H e
0
• Principio di misura:
• sfruttando la relazione che lega il fattore di propagazione dell’onda
nel dielettrico con la sua permittività dielettrica complessa, è
possibile ricavare la parte reale ed immaginaria di quest’ultima da
una misura (non descritta in questa sede) dei parametri di
propagazione dell’onda nel mezzo stesso:
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
242
Metodi di misura di proprietà dielettriche
2. Metodi di misura a circuito a parametri distribuiti:
• Metodo a linea di trasmissione (o a trasmissione d’onda):
• Equazioni dei fasori del campo elettrico e magnetico:
• per un’onda elettromagnetica piana, che si propaga in direzione x in
un mezzo uniforme e infinito, valgono le seguenti espressioni:
~ (ω )2
~ 2 (ω )
γ
γ
1
~
(
α 2 (ω ) − β 2 (ω ) + 2 jα (ω )β (ω ))
ε r (ω ) = 2
=− 2
=− 2
γ 0 (ω )
β 0 (ω )
β 0 (ω )
⇓
⎧ '
β 2 (ω ) − α 2 (ω ) β 2 (ω ) ⎛ α 2 (ω ) ⎞ λ20 (ω ) ⎛ α 2 (ω ) ⎞
⎜⎜1 − 2
⎟⎟
⎜⎜1 − 2
⎟⎟ = 2
= 2
⎪ε r (ω ) =
2
β 0 (ω )
β 0 (ω ) ⎝ β 0 (ω ) ⎠ λ (ω ) ⎝ β 0 (ω ) ⎠
⎪
⎨
2
(ω ) 2α (ω ) λ20 (ω ) 2α (ω )
β
2α (ω )β (ω )
⎪ ''
⎪ε r (ω ) = β 2 (ω ) = β 2 (ω ) β (ω ) = λ2 (ω ) β (ω )
0
0
⎩
• Indice di rifrazione del mezzo:
Davide Micheli
λ0 (ω )
n(ω ) =
λ (ω )
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
243
Definizione di conduzione elettrica
dal punto di vista atomico
Orbitali do Bloch
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
244
Conduzione elettrica nei metalli: orbitali di Bloch
Orbitali delocalizzati nei metalli
•
•
Le proprietà e la struttura dei metalli rivelano che gli elettroni di valenza dei
loro atomi sono delocalizzati, cioè diffusi per tutta l’esenzione del reticolo
cristallino, liberi di muoversi sotto l’azione di un campo elettrico anche molto
debole.
Quando gli orbitali atomici degli atomi componenti una molecola si
sovrappongono apprezzabilmente l’uno con l’altro, la loro combinazione
determina un sistema di orbitali molecolari delocalizzati, estendentesi cioè su
un insieme di più atomi o addirittura su tutti gli atomi della molecola.
• Orbitali 2s di un filare di atomi di litio
del suo reticolo cristallino
• Formazione di un orbitale molecolare
delocalizzato esteso su tutto il filare
medesimo
A
B
C
D
Davide Micheli
E
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
245
Conduzione elettrica nei metalli: orbitali di Bloch
Orbitali delocalizzati nei metalli
•
•
•
Un cristallo metallico, può essere considerato come una molecola gigante
formata da un numero grande di atomi per la quale vale lo stesso prinicpio.
In tal caso data la compattezza della struttura si realizza un esteso
ricoprimento degli orbitali di valenza dei singoli atomi così che gli orbitali
cristallini o reticolari sono completamente delocalizzati ed abbraciano tutto il
reticolo
Questi orbitali delocalizzati che descrivono la distribuzione degli elettroni di
valenza degli atomi nel reticolo cristallino di un metallo sono generalmente
designati come funzioni d’onda di Bloch, dal nome dell’autore che li
introdusse.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
246
Conduzione elettrica orbitali di Bloch
Bande di energia
•
•
•
•
•
•
Gli orbitali molecolari di un cristallo, cioè di un insieme di un numero
grandissimo di atomi, differiscono da quelli propri di una molecola di pochi
atomi per una caratteristica molto importante relativa ai livelli energetici ad
essi corrispondenti.
Per rendercene conto immaginiamo di costruire il reticolo di un cristallo, per
esempio di Sodio (Na), addizionando successivamente un atomo all’altro.
Quando ad un primo atomo A se ne addiziona un secondo, B, costituendo
l’aggregato biatomico A-B (Na2), i due orbitali di valenza dei due atomi si
combinano insieme determinando due orbitali molecolari, ciascuno con una
sua proprio energia.
:
ψ A +ψ B
e
ψ A −ψ B
Energia più alta di quella degli orbitali atomici originari per il primo, più bassa
per il secondo.
Se ora addizioniamo un terzo atomo, realizzando l’aggregato Na3, gli orbitali di
valenza dei tre atomi determinano tre orbitali molecolari, i cui livelli energetici
distinti si raggruppano attorno al livello originario di ψA.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
247
Conduzione elettrica: orbitali di Bloch
Bande di energia
•
•
•
L’aggiunta di ogni nuovo atomo fa aumentare di uno il numero degli orbitali
molecolari risultanti e dei corrispondenti livelli energetici.
Per un insieme di N atomi si avranno dunque N orbitali molecolari ed N livelli
energetici.
Per N molto grande, dell’ordine di 1023, i livelli sono così ravvicinati l’uno
all’altro da costituire una banda continua.
1
•
2
3
4
5
1023
Ad ogni orbitale atomico di un singolo atomo isolato corrisponde, nel cristallo,
una banda di livelli energetici (tanti quanti sono gli atomi dell’insieme).
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
248
Conduzione elettrica: orbitali di Bloch
Bande di energia
•
Le proprietà del cristallo sono determinate dalla differenza di energia fra le
successive bande e dalla distribuzione in esse degli elettroni:
–
Energia
–
La larghezza di queste bande risultanti dalla interazione tra gli atomi nel cristallo
e la separazione tra l’una e l’altra dipendono dalla distanza internucleare (r).
A mano a mano che (r) diminuisce, aumenta la Larghezza e si riduce la
separazione tra bande.
Separazione
tra bande
Banda di conduzione
Na: 1s2, 2s2, 2p6,3s1
3p
3p
3s
valenza
3s
conduzione
Banda di valenza
2p
2p
2s
1s
3.7
1
2
3
4
5
6
7
Distanza interatomica in Angstrom
Davide Micheli
2s
Bande
interne
sature
1s
Successione delle bande
per il sodio metallico (
r=3.7 Angstrom)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
249
Conduzione elettrica: orbitali di Bloch
Bande di energia
•
•
•
Quando gli atomi sono a distanza molto grande l’uno dall’altro e non
interagiscono, i livelli energetici degli elettroni sono quelli propri degli orbitali
dell’atomo isolato.
Diminuendo la distanza interatomica, ogni livello origina una banda che si
allarga con l’aumentare della reciproca interazione tra gli atomi.
Quanto più estesi sono gli orbitali atomici che si considerano, tanto maggiore
è la distanza internucleare alla quale la loro interazione trasforma i livelli
energetici degli atomi isolati in bande:
–
•
•
Per questa ragione i livelli degli orbitali 3s e 3p si allargano in bande già per valori
di r per i quali i livelli degli orbitali 2s e 2p non risultano ancora perturbati e il
livello dell’orbitale interno 1s resta inalterato fino a distanze internucleari molto
piccole.
Conseguentemente per una data distanza r fra gli atomi le bande son tanto più
allargate quanto più alta è la loro energia.
Il progressivo allargamento delle bande col dimiuire della distanza
interatomica può determinare la loro sovrapposizione:
–
Nel caso del sodio a cui si riferisce la figura, alla distanza alla quale si trovano gli
atomi del reticolo (r=3.7 Angstrom) ciò accade per le bande 3s e 3p, che si
fondono in un’unica banda
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
250
Conduzione elettrica: orbitali di Bloch
Bande di energia: distribuzione degli elettroni
•
Gli elettroni degli atomi del cristallo si distribuiscono negli orbitali
corrispondenti ai livelli energetici delle varie successive bande, secondo il
principio di Pauli, cominciando da quelli a più bassa energia.
–
•
•
Riferendoci al caso del sodio, gli elettroni interni degli orbitali 1s,2s,2p saturano
le corrispondenti (bande interne), mentre gli elettroni di valenza 3s (N in tutto)
saturano i primi N/2 livelli della banda 3s (detta perciò banda di valenza; in
chimica è la banda interessata alla cessione, acquisto, condivisione di elettroni
per formare legami chimici)
La successione delle varie bande a energia crescente è intervallata da fasce di
valori di energia proibiti per gli elettroni del cristallo, come proibiti per gli
elettroni di un atomo isolato sono i valori di energia intermedi fra quelli dei
successivi livelli quantizzati.
Gli elettroni che occupano le bande interne sono praticamente localizzati entro
gli atomi a cui appartengono; quelli della banda di valenza, invece, sono
delocalizzati, nel senso che possono muoversi per tutta l’estensione del
reticolo.
–
Per rendersene conto si può osservare l’esempio che segue, relativo ad un atomo
di sodio isolato (figura sinistra) e nel reticolo (figura destra)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
251
Conduzione elettrica: orbitali di Bloch
Bande di energia: distribuzione degli elettroni
•
Per un atomo isolato, è riportata la curva di energia potenziale di un elettrone
nel campo attrattivo del nucleo in funzione della distanza r
(ECoulomb= -Ze2/r =-11e2/r).
Sulla curva sono indicati i livelli energetici relativi agli elettroni dell’atomo:
–
quanto più alto è il livello dell’orbitale occupato, tanto più questo è esteso e
cresce la distanza media dell’elettrone dal nucleo.
E=0
Energia
•
3p
3s
2p
2s
1s
r=0
Distanza dal nucleo
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
252
Conduzione elettrica: orbitali di Bloch
Bande di energia: distribuzione degli elettroni
In figura è rappresentato l’andamento schematico dell’energia potenziale di un
elettrone nel campo periodico dei nuclei in un filare atomico
monodimensionale, e sono indicate le bande di energia permesse:
–
Tra atomo e atomo il campo determina una barriera di energia che isola soltanto
gli elettroni delle bande più interne, caratterizzati da energia troppo bassa per
valicarla, mentre gli elettroni della banda di valenza non ne sono imprigionati e
possono liberamente spostarsi attraverso il reticolo.
E=0
Banda di conduzione
Energia
•
Banda di valenza
3p
3s
barriera
di energia
2p
2s
1s
Campo periodico dei nuclei in un filare atomico monodimensionale di sodio
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
253
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori
•
•
il modello a bande si applica a tutti i solidi cristallini, metallici o no, ed è
particolarmente efficace per l’interpretazione delle loro proprietà di conduttori
o isolanti.
Consideriamo un cristallo ideale, supponendo che le bande elettroniche siano
tutte sperate, senza reciproche sovrapposizioni.
Distribuendo gli elettroni sui livelli permessi, cominciando da quelli inferiori, si
possono verificare le situazioni limite schematizzate nella figura sotto:
•caso a)
•caso b)
Banda vuota
Banda vuota
Banda
Di valenza
non satura
Energia
•
Banda
Di valenza
satura
Bande
Interne
sature
Bande
Interne
sature
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
254
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori
•
•
•
La banda di valenza del caso a) è solo in parte occupata e contiene livelli
ancora liberi, nel caso b) essa è totalmente riempita.
Gli orbitali corrispondenti ai livelli della banda di valenza sono, in entrambi i
casi, delocalizzati e gli elettroni che li occupano sono perciò liberi di spostarsi
da un atomo all’altro, in questa o in quella direzione, ma l’effetto
dell’applicazione di un campo elettrico è ben diverso nelle due situazioni.
Il campo elettrico applicato tende a convogliare gli elettroni liberi in un flusso
unidirezionale che comporta un aumento dell’energia degli elettroni che vi
partecipano:
–
–
Nel caso a) questo può essere realizzato, perché la banda di valenza ha livelli
energetici disponibili al di sopra di quelli occupati in assenza del campo elettrico.
In questi livelli liberi, un campo anche debole, può promuovere un gran numero di
elettroni, determinandone un flusso ordinato nella propria direzione.
Nel caso b) invece questa promozione è impossibile essendo la banda di valenza
del tutto satura, con un gran numero di elettroni ,in media, che si muovono in
tutte le direzioni, senza possibilità di essere trascinati preferenzialmente enlla
direzione del campo, per la mancanza di livelli più alti disponibili a cui dovrebbero
trasferirsi per seguirne la sollecitazione.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
255
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori
•
•
Nel caso a), il cristallo è un conduttore (conduttore elettronico), perché un
campo elettrico anche debole determina un flusso di elettroni attraverso la sua
massa, e quindi il passaggio di una corrente elettrica I=dQ/dt.
Nel caso b), invece, è un isolante. Infatti l’unico mdo per ottenere un flusso
unidirezionale di elettroni, sarebbe l’imposizione di un campo elettrico tanto
intenso da fornire ad una parte degli elettroni di valenza un’energia sufficiente
per trasferirli dalla banda satura alla banda successiva libera (che può essere
definita banda di conduzione perché quando gli elettroni passano ad essa si
ha un flusso di corrente:
–
•
•
Questo meccanismo spiega la tensione di rottura dei dielettrici.
Concludendo, si può dire in generale che se un cristallo è caratterizzato da
bande elettroniche solo parzialmente piene, esso è un conduttore;
Se invece è caratterizzato da bande completamente piene o bande
completamente vuote, senza reciproche sovrapposizioni, è isolante.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
256
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori: ESEMPI
•
Nel LITIO cristallino (1s2, 2s1), le bande 2s e 2p si sovrappongono
parzialmente, formando insieme una banda unica in cui se N è il numero degli
atomi del cristallo, potrebbero distribuirsi 8N elettroni (ad ogni livello della
banda 2p corrispondono infatti 3 orbitali degeneri px, py,pz).
Gli elettroni di valenza sono in tutto N e saturano i primi N/2 livelli della banda
2s, lasciando completamente vuoti gli altri N/2 livelli della banda stessa e tutti i
livelli della banda 2p:
–
Immediatamente al di sopra del più altro livello occupato ci sono dunque molti
altri livelli liberi disponibili per la conduzione sotto l’azione di un campo elettrico.
Atomo
isolato
Energia
•
2p
cristallo
2p
2s
2s
1s
1s
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
257
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori: ESEMPI
•
•
il Carbonio sottoforma di diamante, silicio e germanio, sono caratterizzati, da
un sistema di bande nel quale quella più alta occupata è satura e quella
successiva vuota è separata da un intervallo più o meno largo di valori di
energia proibiti.
Ad esempio nel caso del Diamante, gli atomi di carbonio sono legati l’uno
all’altro in un reticolo covalente, con coordinazione tetraedrica determinata da
orbitali ibridi Sp3. Gli orbitali molecolari risultano in due raggruppamenti, di
legame ed antilegame i cui livelli energetici si raccolgono in due bande
separate da un largo intervallo proibito (pari a 5.6 eV).
Energia
Cristallo di diamante
Atomi di
carbonio
isolati
2 N orbitali di
anti legame
5.6 eV
Orbitali atomici sp3
(N atomi)
2 N orbitali di
legame
Davide Micheli
• I 4N elettroni di valenza
degli atomi del reticolo
saturano completamente
la banda inferiore
lasciando vuota quella
superiore alla quale
tuttavia nessun elettrone
può essere trasferito sotto
l’azione di un campo
elettrico per la grande
distanza tra le due bande.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
258
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori: ESEMPI
•
•
Energia
•
Nel silicio e germanio, i cui cristalli sono coordinati tetraedicamente, la
situazione è simile tuttavia l’ampiezza della bandgap tra banda di valenza
piena e quella di conduzione vuota è rispettivamente di 1.1 (Si) e 0.7 eV (Ge).
La bandgap è molto più piccola di quella del diamante ed è possibile il
trasferimento di un certo numero di elettroni dall’una all’altra, o per
eccitazione termica o per irraggiamento con radiazioni di adatta lunghezza
d’onda.
In queste condizioni il cristallo diventa conduttore e nel primo caso si parla di
termoconduzione mentre nel secondo di fotoconduzione.
• Le sostanze cristalline con
queste caratteristiche sono
Cristallo
2 N orbitali di
dette
semiconduttori
anti legame
intrinseci.
• È da considerare che con il
trasferimento di elettroni
dalla banda di valenza alla
1.1 (Si) e 0.7 eV (Ge). successiva,
vengono
a
partecipare alla conduzione
gli elettroni di entrambe le
bande, perché entrambe
2 N orbitali di
vengono ad avere livelli
legame
vacanti.
Atomi di
silicio i
germanio
isolati
Orbitali atomici sp3
(N atomi)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
259
Conduzione elettrica: orbitali di Bloch
Conduttori, Isolanti, Semiconduttori: ESEMPI
•
La conduzione determinata dagli elettroni della banda che prima era vuota è
detta di tipo n, perché viene trattata come moto di cariche negative, mentre la
conduzione dovuta agli elettroni della banda di valenza non più satura è data
di tipo p, perché pur essendo conduzione anch’essa dei elettroni, è preferibile
trattarla come moto delle lacune positive lasciate dagli elettroni (eccitati)
promossi alla banda superiore di cnduzione:
–
Il movimento degli elettroni della banda di valenza sotto l’azione del campo
equivale alla migrazione, in direzione opposta, delle lacune.
Banda di
conduzione
elettrone
lacuna
Banda di
valenza
Davide Micheli
Il meccanismo della conduzione
elettronica nei semiconduttori lascia
intendere perché, a differenza dai
metalli, la loro conducibilità aumenta
con l’aumentare della temperatura
(ossia diminuisce la loro resistenza):
Infatti, crescendo la temperatura
si esalta per eccitazione termica
il numero degli elettroni che
dalla banda di valenza si
trasferiscono a quella di
conduzione.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
260
Conduzione elettrica: orbitali di Bloch
Semiconduttori drogati
•
•
•
•
•
•
La conducibilità di un cristallo semiconduttore può essere notevolmente
influenzata dall’aggiunta di piccolissime quantità (dell’ordine di qualche parte
per milione) di elementi estranei, i cosiddetti droganti.
Anche un cristallo normalmente isolante, se opportunamente drogato, può
acquisire le caratteristiche di un semiconduttore.
Il caso più comune di droganti è dato da impurezze sostituzionali, cioè di
atomi di altri elementi che vanno a sostituirsi ad atomi del reticolo cristallino
in cui sono introdotti.
Per il silicio o il germanio i droganti più tipici sono il B, Al, Ga, In, Ti e P, As,
Sb, Bi.
Con l’introduzione degli atomi del drogante nuovi livelli elettronici permessi
(livelli di impurezza) vengono ad interporsi tra la banda di valenza e quella di
conduzione nell’intervallo vietato, giocando ruoli diversi secondo la natura del
drogante.
Se gli atomi introdotti hanno più elettroni di valenza di quelli del reticolo
ospitante, (come per esempio accade drogando il silicio o il germanio con il
fosforo) essi agiscono da donatori di elettroni; se invece ne ahnno di meno
(come il boro), agiscono da accettori di elettroni.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
261
Conduzione elettrica: orbitali di Bloch
Semiconduttori drogati
•
Se il semiconduttore agisce da donatore di elettroni allora l’eccesso di
elettroni si distribuisce in livelli situati in prossimità della banda di
conduzione, dai quali possono ad essa trasferirisi per assorbimento di una
piccola quantità di energia. Il semiconduttore è in tal caso detto di tipo n.
Se il semiconduttore agisce da accettore, invece, si rendono disponibli, in
prossimità della banda di valenza, nuovi livelli vacanti, a cui possono
trasferirsi elettroni della banda medesima, determinando in essa delle lacune,
e il semiconduttore è detto di tipo p.
Semiconduttori
intrinseci.
Semiconduttore
di tipo n
energia
•
Semiconduttore
di tipo p
Banda di conduzione
Livelli energetici
degli atomi droganti
Banda di valenza
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
262
Definizione secondo Maxwell di
materiale conduttore e di materiale
dielettrico
Effetto pelle
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
263
Effetto pelle
•
•
Cosa succede al campo elettromagnetico nei conduttori ?
Per rispondere si parte dalla definizione di corrente di conduzione
mediante la legge di Ohm in un conduttore, e dalla seconda equazione
di Maxwell:
Densità Corrente di Conduzione
r
r ⎡ A⎤
⎡1⎤
Legge di OHM : J = σE ≡ ⎢ 2 ⎥ dove : σ = conducibilità [Siemens] = ⎢ ⎥
⎣m ⎦
⎣Ω⎦
r
⎧r r
∂B
r r
r
⎪⎪∇ × E = −
⎧⎪∇ × E = − jωµH
∂t
II e III eq Maxwell : ⎨
r ⇒ per segnali sinusoidali : ⎨ r r r
r
r r r
⎪⎩∇ × H = J + jωεE
∂E
⎪∇
×H = J +ε
⎪⎩
∂t
Densità Corrente di Spostamento
r
r
r
∂E ∂εE ∂D ⎡ F 1 V ⎤ ⎡ C 1 V ⎤ ⎡ C 1 ⎤ A
=
=
≡⎢
=⎢
=⎢
= 2 = Densità Corrente Spostamento
ε
2⎥
⎥
⎥
∂t
∂t
∂t ⎣ m s m ⎦ ⎣Vm s m ⎦ ⎣ s m ⎦ m
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
264
Effetto pelle
•
Sostituendo la legge di Ohm nella seconda eq di Maxwell si ottiene:
r
r
J = σE
r r r
r
r
r
r
⎡ ⎛
σ ⎞⎤ r
⎟⎟⎥ E = jωε~
∇ × H = J + jωεE = σE + jωεE = (σ + jωε 0ε r )E = jω ⎢ε 0 ⎜⎜ ε r +
jωε 0 ⎠⎦
⎣ ⎝
•
•
•
Nello spazio la corrente di conduzione e di spostamento sono
parallele,
Nel tempo corrente di conduzione e di spostamento sono sfasate di
90° infatti j=e(+jπ /2) quindi la corrente di spostamento è in anticipo di
fase di 90° rispetto alla corrente di conduzione.
DOMANDA: secondo MAXWELL che cosa è un conduttore ?
–
•
•
Il rame è sempre un conduttore oppure no ?
L’unica definizione corretta di conduttore è la seguente:
Conduttore è quel materiale per cui la corrente di conduzione è molto
grande rispetto alla corrente di spostamento:
σ >> ωε
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
265
Effetto pelle
•
Per il rame:
σ Cu
•
S
= 10 ÷10
m
10 = σ >> ω ⋅10
•
7
ε ≅ 10-11
ω = 2π ⋅ frequenza
A frequenze basse (ω piccola) il rame risulterà certamente un
conduttore e lo rimarrà fintanto che:
6
•
6
−11
cioè
ω << 10 rad / s cioè
17
1 17
f << 10 Hz
2π
Mano a mano che aumenta la frequenza f, la corrente di conduzione
resta costante, mentre la corrente di spostamento cresce con la
frequenza: dunque esiste una frequenza oltre la quale il rame non
risulta più essere conduttore. Pertanto la precedente definizione va
rettificata:
Conduttore è quel materiale per cui la corrente di conduzione è molto
grande rispetto alla corrente di spostamento, fino alla frequenza f per
cui vale ancora la relazione σ >>ωε
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
266
Effetto pelle
•
•
•
•
•
Si riportano alcuni esmpi con dei materiali diffusi in natura:
Il Rame a conducibilità σ = 5.8⋅107 S/m si comporta come conduttore
fino a frequenze ottiche.
L’acqua di mare è un buon conduttore fino a circa 890 MHz.
Un transistor di silicio che lavora a 20 GHz fa capire che a tale
frequenza il silicio non può più essere trattato come semiconduttore
ma diventa un dielettrico come tutti gli altri.
Pertanto in generale non esistono né conduttori puri, né dielettrici
puri:
–
esistono esclusivamente dielettrici con perdite, cioè dielettrici in cui c’è
una corrente di conduzione; ed allora, se prevale ωε vengono chamati
“DIELETTRICI”, mentre se prevale il termine σ, vengono chiamati
“CONDUTTORI”, altrimenti vengono definiti “DIELETTRICI con
PERDITE”.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
267
Effetto pelle
•
Data la definizione corretta di conduttore si consideri ora l’altra
equazione di Maxwell:
r
r r
∇ × E = − jωµH
•
Applicando l’operatore di rotore ad entrambi i membri si ottiene:
(
)
(
r r r
r r
∇ × ∇ × E = − jωµ ∇ × H
•
)
Ricordando che in un conduttore, la corrente di spostamento è
trascurabile rispetto alla corrente di conduzione, allora sostituendo il
secondo membro si ottiene:
(
)
(
(
) (
)
( )
r r r
r r
r
∇ × ∇ × E = − jωµ ∇ × H = − jωµ σE
ovvero :
r r r r r r
r
r
2
∇ × ∇ × E = ∇ ∇ ⋅ E − ∇ E = − jωµ σE
•
)
( )
Il rotore di un rotore è uguale al gradente della divergenza meno il laplaciano
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
268
Effetto pelle
(
r r
r r r
r ∇× H
r r r r ⎛ ∇⋅ ∇× H
ma E =
⇒ ∇ ∇ ⋅ E = ∇⎜⎜
σ
σ
⎝
r r r
r
r
2
⇒ ∇ × ∇ × E = 0 − ∇ E = − jωµ σE
r
r
2
⇒ ∇ E = jωµ σE
(
(
•
)
)
( )
( )
)⎞⎟ = 0
⎟
⎠
Nel caso di mezzi CONDUTTORI l’equazione d’onda è:
r
r
∇ E − jωµσE = 0
2
•
Nel caso delle onde piane, l’equazione d’onda nel caso di mezzi
DIELETTRICI è:
r 2r
∇ E+k E =0
2
Davide Micheli
dove k 2 = ω 2 µε
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
269
Effetto pelle
•
Moltiplicando entrambi i membri per σ, e riconoscendo che J= σE si
ha:
r
r
∇ σE − jωµσσE = 0
2
r
r
⇒ ∇ J − jωµσJ = 0
2
•
Questa è l’equazione d’onda per la densità di corrente in un
conduttore.
•
Essa è una equazione vettoriale, che dunque si compone nelle 3
componenti Jx,Jy,Jz. Il laplaciano è la somma delle derivate seconde
rispetto ad x, rispetto ad y, rispetto a z.
(
∇ 2 J xiˆ + ∇ 2 J y ˆj + ∇ 2 J z kˆ = jωµσ J xiˆ + ∇ 2 J y ˆj + ∇ 2 J z kˆ
)
⎞
⎞ˆ ⎛ ∂2
⎛ ∂2
∂2
∂2
∂2
∂2
⎜⎜ 2 J x + 2 J x + 2 J x ⎟⎟i + ⎜⎜ 2 J y + 2 J y + 2 J y ⎟⎟ ˆj +
∂y
∂z
∂y
∂z
⎠
⎠ ⎝ ∂x
⎝ ∂x
(
⎛ ∂2
⎞ˆ
∂2
∂2
+ ⎜⎜ 2 J z + 2 J z + 2 J z ⎟⎟k = jωµσ J xiˆ + ∇ 2 J y ˆj + ∇ 2 J z kˆ
∂z
∂y
⎝ ∂x
⎠
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
)
270
Effetto pelle
•
•
Studiamo un caso semplice, si supponga che il conduttore sia un
piano indefinito ovvero un semispazio in x ed y; la corrente su tale
piano, sia tutta uniforme, e diretta in una sola direzione z: questo
perché si suppone l’esistenza di una sorgente che genera una corrente
uniforme (ad esempio un onda piana che incide normalmente).
Supponiamo il caso sinusoidale ovvero;
r
r
J 0 = σE = σE0e jωt
•
Si vuole sapere cosa accade alla corrente in profondità, tenendo
presente che la corrente viene mantenuta costante e parallela a se
stessa sulla superficie di quel semispazio infinito. J ha una unica
yx z
componente Jz.
J
Davide Micheli
0
=
σ
E
=
σ
E
0
e
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
271
Effetto pelle
•
•
•
La corrente non varia né lungo z, né lungo y e si vuole vedere cosa
succede andando in profondità lungo la direzione x.
Delle tre componenti Ex,Ey,Ez l’unica non nulla è Ez; la derivata
seconda (nel Laplaciano) rispetto a z è nulla (perché è costante lungo
z), così come rispetto ad y (perché è costante rispetto ad y)
Il laplaciano diviene pertanto la derivata di Ez rispetto ad x due volte:
2
r
r
d
Ez
2
2
2
∇ E = jωµσE ⇒
=
j
ωµσ
E
=
τ
E
con
τ
∈C
z
z
2
dx
•
L’equazione differenziale della corrente è identica:
2
r
r
d
Jz
2
2
2
∇ J = jωµσJ ⇒
=
j
ωµσ
J
=
τ
J
con
τ
∈C
z
z
2
dx
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
272
Effetto pelle
•
Per trovare quanto vale τ occorre fare la radice quadrata:
jωµσ = τ 2 con τ 2 ∈ C
τ = ± jωµσ = ± j 2π fµσ = ± 2 j π fµσ
ma :
1
2
π
j
⎛ j π2 ⎞
π
π
2
2
4
j = ⎜⎜ e ⎟⎟ = e = cos + j sin =
+j
4
4
2
2
⎝
⎠
1
2
⎛ 2
2⎞
⎟ = 1+ j
⇒ 2 j = 2 ⎜⎜
+j
⎟
2
2
⎝
⎠
⇒ τ = ±(1 + j ) π fµσ
•
•
Nella relazione trovata la quantità
profondità di penetrazione.
Si misura in m.
Davide Micheli
1
δ=
π fµσ
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
è chiamata
273
Effetto pelle
•
La soluzione dell’equazione differenziale omogenea
d 2 Ez
2
=
τ
Ez
2
dx
•
È data da due esponenziali, uno positivo (esponente +τx) e l’altro
negativo (esponente - τx).
Ez = c1e
•
−τx
+ c2e
+τx
(
1+ j)
doveτ = ±
δ
Avendo deciso di prendere la radice con parte reale positiva si ha che
il temine moltiplicato per c1 all’infinito tende a zero mentre l’altro
termine risulta non essere limitato (ossia divergente per x→+∞).
− τx
c
e
lim 1 = 0
x →+∞
•
eq differenziale omogenea
+τx
c
e
lim 2 = +∞
x →+∞
La condizione di Sommerfeld dice che ogni campo elettromagnetico
fisicamente realizzabile deve andare a zero almeno come 1/r e quindi
non può divergere, ne segue che c2=0, in questo modo il termine
divergente moltiplicato per c2 è nullo e la condizione di Sommerfeld è
verificata.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
274
Effetto pelle
•
Pertanto la soluzione è
E z = c1e
•
•
•
•
−x
1+ j
δ
= E0 e
−
x
δ
⋅e
−
jx
δ
È da questa ultima relazione che si deduce che δ si misura in metri,
infatti se nell’esponenziale c’è x/δ questo implica che δ deve avere le
dimensioni di x cioè metri.
Ogni materiale conduttore, ad ogni frequenza ha una profondità di
penetrazione che è quella per la quale il campo elettrico si riduce di 1/e
di quello in superficie (cioè la corrente si riduce di 1/e)
La corrente dunque è massima in superficie, poi, man mano che si va
in profondità, essa si mantiene sempre parallela a se stessa, però
diminuisce in ampiezza come e-x/δ e si sfasa in ritardo come e-jx/δ .
Pertanto un pezzo di conduttore non è mai una resistenza pura, ma
sarà una resistenza più un induttanza che provoca la corrente in
ritardo in profondità.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
275
Effetto pelle
•
•
Interessa ora calcolare una quantità chiamata resistenza per quadro.
Per calcolare tale quantità è necessario calcolare prima la corrente
totale facendo un integrale della densità di corrente:
∞
I ( z) = ∫ J 0 e
Cioè:
−
x
δ
⋅e
−
jx
δ
dx
0
(1+ j ) x
r ∞ − (1+ j )x
r ∞⎡
−
⎤
d
δ
δ
δ
I ( z) = J 0 ∫ e
dx = J 0 ∫ ⎢−
e
⎥ dx
(1 + j ) dx
0
0⎣
⎦
∞
r − δ ∞ ⎡ − (1+ j )x ⎤ r − δ ⎡ − (1+ j ) x ⎤
r −δ ⎡ 1 1 ⎤ r δ
δ
δ
= J0
− 0 ⎥ = J0
d ⎢e
⎥ = J0
⎢e
⎥ = J0
∞
∫
⎢
(1 + j ) 0 ⎣
(1 + j ) ⎣
(1 + j ) ⎣ e e ⎦
(1 + j )
⎦
⎦0
r
r
Poiché J = σE
r
E z0 =
Si può calcolare il campo elettrico:
r
J0
σ
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
276
Effetto pelle
•
•
•
•
A questo punto si può introdurre il concetto di resistenza quadro. Si
supponga di prendere un quadrato di conduttore con le seguenti
dimensioni: 1 m lunghezza, 1 m larghezza (si parla di resistenza per
quadro proprio perché il conduttore viene preso quadrato!).
L’impedenza in una mattonella è data dalla tensione diviso per la
corrente.
La tensione è data dal campo elettrico per 1 m, ovverosia Ez0.
La corrente è l’integrale fatto in precedenza.
Facendo il rapporto tensione corrente si ha:
Zs =
•
r
E z0
r
J0
σ
1+ j
= r
=
= Rs + jωLs
I ( z) J ⋅ δ
σδ
0
1+ j
Quindi un conduttore di 1m per 1m non si comporta come una
resistenza pura, ma come una resistenza con in serie una induttanza.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
277
Effetto pelle
•
Nella equazione precedente l’impedenza non è trascurabile, la
resistenza è 1/σδ, mentre la reattanza è 1/σδ, (sono identiche!)
Zs =
1+ j
σδ
= Rs + jωLs =
RS
1
σδ
+j
1
σδ
⇒
LS
⎛ 1
⎜
−1 σδ
ϕ = tg ⎜
⎜ 1
⎜
⎝ σδ
⎞
⎟
⎟ = 45°
⎟
⎟
⎠
La parte immaginaria dell’impedenza produce uno sfasamento dell’onda
EM di 45° in ritardo
•
Ricordando che :
1
δ=
π fµσ
•
π fµσ
π fµ
1
=
=
=
Rs =
1
σδ σ
σ
σ
π fµσ
1
•
Si ha:
[Ω]
Quindi in un blocco di conduttore, la resistenza cresce con la radice
quadrata della frequenza !
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
278
Effetto pelle
•
La resistenza per quadro dipende solo dal materiale e dalla frequenza,
si consideri infatti un quadro di (1m x 1m), la resistenza vale:
l
R= ρ⋅
S
1
dove ρ =
σ
ma S = l ⋅ t
resistività e S = sezione attraversata dalla corrente.
1
l
=
R= ρ⋅
l ⋅t σ ⋅t
⇒
t
S
l
l
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
279
Effetto pelle
•
Tenendo presente che la corrente sul conduttore diminuisce come :
e
−
t
δ
•
Si hanno due casi:
•
1) se lo spessore fisico del conduttore è molto piccolo rispetto a δ
(che è funzione della frequenza ed aumenta a basse frequenze) allora
la corrente è uniformemente distribuita su tutta la sezione del
conduttore.
1
δ=
π fµσ
•
2) aumentando la frequenza, se lo spessore è grande rispetto a δ, la
corrente in definitiva si mantiene sullo spessore esterno (in profondità
non c’è più)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
280
Effetto pelle
•
Integrando la parte reale della densità di corrente in uno spessore t di
conduttore (non tra 0 e ∞) si ha:
⎛ −1 −δ
I (t ) = ∫ J 0e dx = J 0 (− δ )∫ ⎜⎜ e
δ
0
0⎝
t
−
t
x
x
δ
⎞
⎛ −
⎟dx = J 0 (− δ )∫ d ⎜ e δ
⎟
⎜
0 ⎝
⎠
t
x
t
⎞
⎡ − ⎤
⎟ = J 0 (− δ )⎢e δ ⎥ =
⎟
⎠
⎣ ⎦0
x
t
− ⎤
⎡
⎡ − δt ⎤
= J 0 (− δ )⎢e − 1⎥ = J 0δ ⎢1 − e δ ⎥
⎣
⎦
⎣
⎦
•
Pertanto la resistenza per quadro in funzione della frequenza f è:
E (t )
R[ ] = Re[Z s ] =
=
I (t )
J0
σ
⎡
⎤
J 0δ ⎢1 − e δ ⎥
⎣
⎦
−
π fµ
σ
1
=
=
t
t
− ⎤
− ⎤
⎡
σ ⎡
δ
δ
⎢1 − e ⎥ ⎢1 − e ⎥
π fµ ⎣
⎦ ⎣
⎦
t
=
1
⎡
−
t
⎤
σδ ⎢1 − e δ ⎥
⎣
⎦
1
=
σ
⎧ 1
⎪⎪ σ t
[Ω/Quadro] = ⎨
⎪1
⎪⎩σδ
Davide Micheli
1
π fµσ
⎡
⎤
δ
1
e
−
⎢
⎥
⎣
⎦
−
(per
f → 0)
(per
f → ∞)
t
=
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
281
Effetto pelle
•
•
•
Si osserva dalle precedenti che la resistenza per quadro dipende dallo
spessore t del materiale. Facendo il limite per f→∞ (alte frequenze), ci
si accorge che la resistenza per quadro tende a 1/(σδ): vuol dire che
supponendo di avere una sezione rettangolare del materiale in esame,
a frequenze molto basse esso è tutto pieno di corrente, mentre a
frequenze alte c’è solo uno spessore δ in cui la corrente è significativa.
Al crescere dalla frequenza la resistenza va come 1/(σδ) però δ è
inversamente proporzionale alla √f; quindi la resistenza del conduttore
aumenta con la radice quadrata della frequenza.
Giacché la reattanza interna è uguale ad R, allora anche la reattanza
interna delle piste conduttrici aumenta con la radice quadrata della
frequenza.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
282
Effetto pelle
•
•
•
Come esempio si riporta la resistenza per quadro al variare della
frequenza per due conduttori in rame di spessore 18 e 36 micron.
f
δ
t= 18 µm
t= 36 µm
1 kHz
2.1 mm
0.96 mΩ/□
0.48 mΩ/□
1 MHz
66 µm
1.1 mΩ/□
0.62 mΩ/□
10 MHz
21 µm
1.4 mΩ/□
1.0 mΩ/□
100 MHz
6.6 µm
2.8 mΩ/□
2.6 mΩ/□
1000 MHz
2.1 µm
4.2 mΩ/□
4.2 mΩ/□
A 100 MHz la δ è 6.6 µm, per cui grosso modo lo spessore effettivo è δ,
e non più t; dunque la pista da 18 micron oppure 36 micron
praticamente hanno la stessa resistenza,
Andando più su in frequenza ci si accorge che è perfettamente inutile
realizzare piste più spesse della profondità di penetrazione.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
283
Propagazione libera:
Onde EM in Dielettrici reali
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
284
Onde EM in Dielettrici reali
•
•
•
Per dielettrico reale si intende un dielettrico con perdite.
Tutti i dielettrici hanno una conducibilità σ non nulla
Dalle equazioni di Maxwell per segnali sinusoidali si ha:
r
r
r
⎧
∂B
r r
r
∇
×
E
=
−
⎪⎪
⎧⎪∇ × E = − jωµH
∂t
r ⇒ ⎨r r r
r
⎨
r r
r
⎪⎩∇ × H = J + jωεE
∂E
⎪∇
× H = µJ + µε
⎪⎩
∂t
r
r
J = σE
[
]
r r r
r
r
r jωε 0 r
r
σE + jω (ε 0ε r )E =
∇ × H = J + jωεE = σE + jω (ε 0ε r )E =
jωε 0
⎡ σ
⎡ σ
⎤r
⎡
jω (ε 0ε r ) ⎤ r
σ ⎤r
= jωε 0 ⎢
+
+ ε r ⎥ E = jωε 0 ⎢ε r − j
⎥ E = jωε 0 ⎢
⎥E
ωε 0 ⎦
jωε 0 ⎦
⎣ jωε 0
⎣ jωε 0
⎦
⎣
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
285
Onde EM in Dielettrici reali
Definiamo pertanto la costante dielettrica complessa:
εr = ε '
e
σ
ε ''=
ωε
r r
r
r
⎡
σ ⎤r
~
⇒ ∇ × H = jωε 0 ⎢ε r − j
⎥ E = jωε 0 [ε '− jε ' ']E = jωε E
ωε 0 ⎦
⎣
ε~ = ε 0 [ε '− jε ' '] è la costante dielettrica complessa
•
•
Ci si riconduce la caso senza perdite (σ = 0) a condizione di utilizzare nei
calcoli una ε complessa, la cui parte reale è la costante dielettrica relativa, e la
cui parte immaginaria dipende dalla conducibilità σ e dalla frequenza f.
Normalmente, per esprimere la bontà di un dielettrico si fornisce il tg δ,
espresso da:
per un buon dielettrico reale
tg δ < 10-3
Davide Micheli
σ
ε ' ' ωε 0
σ
tgδ =
=
=
ε'
ε ' ωε 0ε r
σ
cioè ε ' ' =
<< ε '
ωε
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
286
Onde EM in Dielettrici reali
• La permittività, è una quantità comunemente usata per descrivere le proprietà
elettriche che influenzano la riflessione di un’onda elettromagnetica
all’interfaccia tra due mezzi diversi e l’assorbimento dell’energia all’interno dei
materiali.
• La permittività relativa εr di un materiale (data dal rapporto tra la permittività del
materiale ε e quella del vuoto ε0) è un numero complesso espresso secondo la
relazione:
εr = ε’ - jε’’
• La parte reale ε’ (detta anche costante dielettrica) influenza la distribuzione del
campo elettrico e la fase delle onde all’interno del materiale.
• Il coefficiente della parte immaginaria, ε’’ (chiamato non a caso “fattore di
perdita”) influenza, invece, l’assorbimento da parte del materiale dell’energia
trasportata dal campo. E’ proprio ε’’ che determina la quantità di energia che
viene dissipata all’interno di un materiale e, di conseguenza, di quanto riesce ad
aumentarne la temperatura interna.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
287
Onde EM in Dielettrici reali
•
•
Per poter utilizzare la teoria delle linee di trasmissione occorre trovare
l’impedenza del mezzo.
Per determinare l’impedenza di un dielettrico reale si parte come
sempre dalla definizione:
µ
η=
=
ε
µ0 µ r
µ0 µ r
jωε 0 µ0 µr
=
=
=
ε 0 [ jωε 0ε r + σ ]
ε 0 [ jωε 0ε r + σ ]
⎡
σ ⎤
ε 0 ⎢ε r +
⎥
jωε 0
ωε
j
0⎦
⎣
⇓
jωµ0 µr
η=
[ jωε 0ε r + σ ]
•
se σ = 0
allora
jωµ0 µr
µ
η=
=
[ jωε 0ε r ] ε
indipendente da ω
Se σ aumenta, le perdite aumentano e così la dissipazione di potenza.
– L’impendenza η si riduce e aumenta per esempio il salto di impedenza
nel caso che i dielettrici siano aria e dielettrico del mezzo. Di
conseguenza aumenta il coefficiente di riflessione e l’onda incidente
viene maggiormente riflessa.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
288
Onde EM in Dielettrici reali
•
Si possono ora riscrivere le eq delle onde piane; la costante di fase è:
~
ε '' ⎞
ε '' ⎞
⎛
⎛
~
~
k = ω µε = ω µε = ω µε 0 (ε '− jε ' ') = ω µε 0ε ' ⎜1 − j ⎟ = ω µε 0ε ' ⎜1 − j ⎟
ε' ⎠
ε' ⎠
⎝
⎝
x
ma ricordando che dallo sviluppo di Taylor al arrestato al primo term.: 1 + jx ≅ 1 + j
2
~
ε '' ⎞
ε '' ⎞
⎛
⎛
k = ω µε 0ε ' ⎜1 − j ⎟ ≅ ω µε 0ε ' ⎜1 − j ⎟ = β − jα
ε' ⎠
ε' ⎠
⎝
⎝
Dielettrici reali
se : ε ' ' << ε '
⇒
⎧ β = ω µε 0ε ' = k0
⎪
ε ''
ε ''
⎨
⎪⎩ α = ω µε 0ε ' ε ' = k0 ε '
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
289
Onde EM in Dielettrici reali
•
L’onda si propaga come:
e
~
mkz
=e
mαz
⋅e
m jβz
•
Ovvero si propaga con la stessa velocità di fase come se non ci
fossero perdite, vedi termine in jβz, però l’ampiezza si riduce secondo
il termine in α perché, essendoci perdite nel dielettrico, una parte della
potenza dell’onda si dissipa, e si trasforma in calore.
•
Si trova per α la stessa espressione delle linee di trasmissione:
WL
α=
2WT
•
•
WL=potenza dissipata per unità di lunghezza
WT=potenza trasmessa
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
290
Onde EM in Dielettrici reali
•
Il coefficiente di riflessione sul carico L non varia in presenza di
perdite qualunque sia η0 o ηL e formalmente è sempre dato da:
Vt
V+
η0
E(i)
ηL
V-
E(t)
η0
ηL
Zi
E(r)
ηL
vi
z
•
η L − η0
ρL =
η L + η0
Z=0
Il coefficiente di riflessione ad una distanza z dal carico invece risente
del fatto che l’onda si propaga con attenuazione:
V − ( z ) V − (0) ⋅ e +α ⋅z ⋅ e + j⋅β ⋅z V − (0) + 2α ⋅ z + 2 j⋅β ⋅ z
+ 2α ⋅ z
+ 2 j ⋅β ⋅ z
ρ (z ) = + = +
=
e
⋅
e
=
ρ
e
⋅
e
L
V ( z ) V (0) ⋅ e −α ⋅ z ⋅ e − j⋅β ⋅z V + (0)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
291
Onde EM in Dielettrici reali
•
Il coefficiente di riflessione ad una distanza z=-l dal carico dove
supponiamo il punto zero di riferimento per la lunghezza è pertanto:
ρ (z = −l ) = ρ L e +2α ⋅z ⋅ e +2 j⋅β ⋅z = ρ L e −2α ⋅l ⋅ e −2 j⋅β ⋅l
–
–
•
•
L’onda si propaga in una linea di trasmissione con perdite e viene
attenuata in modulo.
La fase del coefficiente di riflessione cambia mano a mano che ci si
sposta lungo la direzione di propagazione secondo il termine βz.
Questo principio viene utilizzato per esempio nel caso di materiali
assorbenti.
Ad esempio una camera anecoica i coni attenuano le riflessioni dovute
alle pareti che si suppongono metalliche. Ogni cono può essere visto
come una linea di trasmissione, all’interno della quale si propaga un
onda EM che subisce quel tipo di attenuazione. Questi coni sono fatti
di materiale che presenta delle perdite Yp nel dielettrico.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
292
Onde EM in Dielettrici reali
•
Supponiamo di considerare come distanza quella pari ad una certa
lunghezza d’onda;
sappiamo che β =
2π
λ
supponiamo due casi :
l1 = λ / 4
l2 = λ / 2
⇓
•
•
ρ1 (z = −λ / 4) = ρ L e + 2α ⋅z ⋅ e + 2 j⋅β ⋅z = ρ L e
− 2α
ρ 2 (z = −λ / 2) = ρ L e
− 2α
+ 2α ⋅ z
⋅e
+ 2 j ⋅β ⋅ z
= ρ Le
λ
4
λ
2
⋅e
−2 j
⋅e
2π λ
λ 4
−2 j
2π λ
λ 2
= ρ Le
− 2α
= ρ Le
− 2α
λ
4
λ
2
⋅ e − jπ = − ρ L e
−α
λ
2
⋅ e − j 2π = ρ L e −αλ
Il coefficiente di riflessione (num complesso) a queste distanze è
costituito dalla sola parte reale
Al variare dalla distanza o parimenti della frequenza il coefficiente di
riflessione varia sia in modulo che in fase
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
293
Onde EM in Dielettrici reali
Parte Reale del Coefficiente di riflessione sul carico e a
distanza 1 m con perdite nel dielettrico
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
Coeff Rifless sul carico.
-0.8
Coeff Rifless dist L(m)
-0.9
2
17
32
47
62
77
92
107
122
137
152
167
182
197
212
227
242
257
272
287
302
317
332
347
362
-1
377
Coeff Rifless sul carico e Coeff Rifless a
distanza 1m
0
Parte reale impedenza del carico ZL
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
294
Onde EM in Dielettrici reali
•
Equivalente linea di
trasmissione di una
camera anecoica
Coni
assorbenti
η3_parete metallica
η1_aria
Parete
metallica
E(i)
η1_aria
l2
η0
η2_dielettrico
Coni
assorbenti
Zi
η2_dielettrico
Parete
metallica
η2
vi
z
ηL
η3_parete metallica
l2
Z=-l2
Z=0
ρL =
η L − η0
η L + η0
ρ (z = −l2 ) = ρ L e −2α ⋅l ⋅ e −2 j⋅β ⋅l
(~ )
( )
(~ )
( )
η cosh k 2 ⋅ l2 + η 2 sinh k 2 ⋅ l2
η ( z = −l2 ) = η 2 3
~
~
η 2 cosh k 2 ⋅ l2 + η3 sinh k 2 ⋅ l2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
295
Onde EM in Dielettrici reali
•
Supponiamo un onda piana che incide normalmente, su 3 dielettrici.
Questo problema per analogia con le linee di trasmissione è
perfettamente riconducibile al problema di incidenza di un onda di
tensione da una linea con una certa impedenza caratteristica ad
un’altra linea con un impedenza caratteristica diversa, si possono
dunque utilizzare tutti gli strumenti usati per le linee.
l2
η1
η2
η3
E(i)
E(r)
+
E(t)
-
=
η1
η2
η3
Zi
l2
•
•
Supponiamo il sistema con perdite.
Consideriamo come carico della
linea 1 l’impedenza risultante della
linea 2 e 3 insieme
Davide Micheli
vi
η2
η3
l2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
296
Onde EM in Dielettrici reali
•
Il circuito equivalente risultante diviene pertanto:
η1
η2
η3
+
E(i)
E(t)
-
E(r)
=
η1
E(r)
η2
η3
Zi
l2
E(i)
η1
vi
η3
l2
Zi
+
η2
E(t)
-
Davide Micheli
=
η1
Zi
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
297
Onde EM in Dielettrici reali
•
•
Si procede calcolando il coefficiente di riflessione all’ingresso della linea
precedente, nonché il coefficiente di riflessione sulla l1 di impedenza η1 .
Allo scopo bisogna prima calcolare l’impedenza Zi: dato che si tratta di una
linea lunga l2 e di impedenza caratteristica η2 chiusa su un carico concentrato
η3, l’impedenza di ingresso Zi sulla sezione i è data da:
(
(
)
)
~
η cosh k 2 ⋅ l2 + η 2 sinh
Zi = η2 3
~
η 2 cosh k 2 ⋅ l2 + η3 sinh
(
(
~
k 2 ⋅ l2
~
k 2 ⋅ l2
)
)
⇓
Z i − η1 E (r ) V (r )
ρ=
= (i ) = (i ) = S11 (coefficiente di riflessione sulla prima interfaccia i )
Z i + η1 E
V
2Z i
E (+ ) V (+ )
τ=
= (i ) = (i ) = S 21 (coefficiente di trasmissione sulla prima interfaccia i )
Z i + η1 E
V
⇓
P (r )
2
ρ = (i ) = S11 (potenza riflessa alla prima interfaccia i )
P
P (+ )
2
2
2
τ = (i ) = 1 − ρ = S 21 (potenza trasmessa alla prima interfaccia i )
P
2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
298
Onde EM in Dielettrici reali
•
•
La somma delle potenze riflessa e della potenza trasmessa è pari alla
potenza incidente meno la potenza dissipata a causa delle perdite sul
dielettrico.
Nel caso di assenza di perdite utilizzando la matrice di Scattering S si
ha:
S11 + S 21 = 1 (assenza di perdite)
2
2
S11 + S 21 < 1 (presenza di perdite)
2
2
dove :
P (r )
2
ρ = (i ) = S11 (potenza riflessa alla prima interfaccia i)
P
P (+ )
2
2
2
τ = (i ) = 1 − ρ = S 21 (potenza trasmessa alla prima interfaccia i)
P
2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
299
Onde EM in Dielettrici reali
Graficando un esempio in cui si riporta un dielettrico con un impedenza
normalizzata a quella dell’aria si ha
Refelction and Transmission coefficient in (linear) as a function of
Normalized impedance
Reflection coefficient(linear)
2.00
Transmission coefficient (linear)
1.50
1.00
0.50
0.09
0.24
0.40
0.56
0.71
0.87
1.03
1.18
1.34
1.50
1.65
1.81
1.97
2.12
2.28
2.43
2.59
2.75
2.90
3.06
3.22
3.37
3.53
3.69
3.84
0.00
4.00
S11 (linear) and S21(linear)
•
-0.50
-1.00
-1.50
Normalized impedance
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
300
Onde EM in Dielettrici reali
Graficando un esempio in cui si riporta un dielettrico con un impedenza
normalizzata a quella dell’aria si ha
Refelction and Transmission coefficient in dB as a function of
Normalized impedance
10.00
0.12
0.28
0.44
0.60
0.76
0.93
1.09
1.25
1.41
1.57
1.73
1.90
2.06
2.22
2.38
2.54
2.71
2.87
3.03
3.19
3.35
3.51
3.68
-10.00
3.84
4.00
0.00
S11 (dB) and S21(dB)
•
-20.00
-30.00
-40.00
-50.00
Reflection coefficient(dB)
Transmission coefficient (dB)
-60.00
-70.00
Dielectric to Air normalized impedance
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
301
Onde EM in Dielettrici reali
•
Supponiamo per esempio che al variare della frequenza, una linea chiusa su
un certo carico, presenti queste caratteristiche:
Riflessione
Trasmissione
Ii
S21
Vi
Zi
ZL
S11
Z=-l
Z=0
Z
Davide Micheli
• In corrispondenza della frequenza di
risonanza di questo filtro, si ha la
minima riflessione (min S11) e la
massima trasmissione (max S21).
• La potenza persa rispetto a quella
incidente, è dissipata nel dielettrico
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
302
Onde EM in Dielettrici reali
•
Supponiamo per esempio che al variare della frequenza, una linea chiusa su
un certo carico, presenti queste caratteristiche:
Riflessione
Trasmissione
Ii
• Avvicinandosi alla frequenza di
risonanza la linea tende a
produrre uno sfasamento delle
onde EM sia trasmesse sia
riflesse.
S21
Vi
η1
η2
η1
S11
Z=-l
Z
Z=0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
303
Onde EM in Dielettrici reali
•
Supponiamo per esempio che al variare della frequenza, una linea chiusa su
un certo carico, presenti queste caratteristiche:
Permittività
Elettrica
Permeabilità
Magnetica
µ
ε
• La parte immaginaria della Permittività Elettrica, rappresenta le perdite nel
dielettrico.
• La parte immaginaria della Permeabilità Magnetica tende mediamente a zero
ovvero il circuito non ha perdite di tipo ferromagnetico.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
304
Onde EM in Dielettrici reali
•
Se gli altri parametri S22 ed S12 sono simili ad S11 ed S21 allora il circuito può
definirsi simmetrico elettricamente
Ii
• Un circuito simmetrico è anche
reciproco, non vale il viceversa.
• Nell’esempio visto il 2-porte si
comporta
elettricamente
simmetricamente alla porta (1) e (2).
S21
Vi
η1
η2
η1
S11
Z=-l
Z
Z=0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
305
Propagazione libera:
Onde EM in Dielettrici ideali
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
306
Onde EM in Dielettrici ideali
•
Se la linea di trasmissione diventa ideale allora la impedenza
d’ingresso assume un valore differente:
I(l)
Z L cos(β 0 ⋅ l0 ) + jZ 0 sin(β 0 ⋅ l0 )
Z i (− l ) = Z 0
Z 0 cos(β 0 ⋅ l0 ) + jZ L sin(β 0 ⋅ l0 )
+
V(l)
ZL
Z0
L
µ
=
Z0 =
C
ε
-
Zi
z
-l0
0
1) Caso particolare di linea adattata: Z0=ZL vale sia per linee con perdite
che senza perdite.
Z i (− l ) = Z 0
Z 0 cos(β 0 ⋅ l0 ) + jZ 0 sin (β 0 ⋅ l0 )
= Z0
Z 0 cos(β 0 ⋅ l0 ) + jZ 0 sin (β 0 ⋅ l0 )
L
µ
Z0 =
=
C
ε
Z L − Z0
ρL =
=0
Z L + Z0
Davide Micheli
• In questo caso il generatore v(-l)
o l’onda incidente E(i), vedono
sempre la stessa impedenza in
qualunque punto della linea.
• Il coefficiente di riflessione è
nullo, non ci sono onde riflesse.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
307
Onde EM in Dielettrici ideali
2) Caso particolare di linea in corto circuito: ZL=0
I(l)
Z L cos(β 0 ⋅ l0 ) + jZ 0 sin(β 0 ⋅ l0 )
Z i (− l ) = Z 0
Z 0 cos(β 0 ⋅ l0 ) + jZ L sin(β 0 ⋅ l0 )
+
V(l)
Z0
(STUB)
ZL
L
µ
=
Z0 =
C
ε
-
Zi
z
-l0
Z i (− l ) = Z 0
Z0 =
0
0 + jZ 0 sin(β 0 ⋅ l0 )
= jZ 0tg (β 0 ⋅ l0 )
Z 0 cos(β 0 ⋅ l0 ) + 0
L
µ
=
C
ε
ρL =
0 − Z0
= −1
0 + Z0
Davide Micheli
• a prescindere dalla lunghezza
della linea l’impedenza è sempre
puramente reattiva
• L’impedenza di questa linea, in
virtù della funzione tangente,
cambia natura a seconda della
lunghezza dello STUB. Può
assumere natura capacitiva o
induttiva.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
308
Onde EM in Dielettrici ideali
2) Caso particolare di linea in corto circuito: ZL=0 (STUB corto circuito)
• In prossimità di l=0 cioè sul carico, l’impedenza totale sarà pari a 0
• Mano a mano che ci si sposta lungo la linea la tg(βl) cambia:
λ =Vfase/f e dipende dal mezzo in cui l’onda si propaga con frequenza f=ω/2π
2π
dove λ0 è la lunghezza d' onda sul mezzo
β0 =
λ0
⎛
l0 ⎞
Z i (− l ) = jZ 0tg ⎜⎜ 2π ⎟⎟
⎝ λ0 ⎠
l0 1
≤
ovvero
1) se 0 ≤
λ0 4
0 ≤ l0 ≤
λ0
2) se
1 l0 1
≤
≤
4 λ0 2
ovvero
3) se
1 l0
=
4 λ0
ovvero l0 =
4) se
1 l0
=
2 λ0
ovvero l0 =
4
λ0
≤ l0 ≤
λ0
4
λ0
2
Davide Micheli
4
λ0
2
⇒ tg positiva ⇒ impedenza immaginaria induttuva
⇒ tg negativa ⇒ impedenza immaginaria capacitiva
⇒ tg tende ad ∞ ⇒ circuito aperto
⇒ tg tende a 0 ⇒ stessa impedenza del carico
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
309
Onde EM in Dielettrici ideali
2) Caso particolare di linea in corto circuito: ZL=0 (STUB corto circuito)
Reattanza al variare di
l/lambda
100.00
80.00
60.00
Reattanza
induttiva
Reattanza
induttiva
Reattanza
induttiva
Reattanza
20.00
-40.00
-60.00
-80.00
L=0
L=λ/4
L=λ/2
Reattanza
capacitiva
1.72
1.64
1.56
1.48
1.40
1.33
1.25
1.17
1.09
1.01
0.94
0.86
0.78
0.70
0.62
0.55
0.47
0.39
0.31
0.23
0.16
-20.00
0.08
0.00
0.00
Reattanza
40.00
L=λ
Reattanza
capacitiva
Reattanza
capacitiva
-100.00
l/lambda
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
310
Onde EM in Dielettrici ideali
3) Caso particolare di linea in corto circuito: ZL=0 (STUB corto circuito
con linea lunga λ/4)
Da quanto visto quando ci si avvicina alla frequenza tale che la
lunghezza fisica della linea è pari a λ/4, l’impedenza di una linea
chiusa in cortocircuito è in realtà quella di un circuito aperto, tende
cioè ad infinito.
4) Quando invece ci si avvicina alla frequenza tale che la lunghezza fisica
della linea è pari a λ/2, l’impedenza di una linea chiusa in cortocircuito
corrisponde al carico di corto circuito, ovvero la linea tende ad essere
trasparente, non introduce quindi alterazioni della impedenza
complessiva.
Quest’ultimo caso è utile per esempio quando si deve costruire una
copertura (radome) di protezione per un antenna. Se si trasmette ad
una frequenza preferenziale allora se lo spessore del radome è
esattamente pari a λ/2, esso non rifletterà nessuna potenza verso
l’antenna e quindi tutta la potenza emessa dall’antenna sarà irradiata.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
311
Onde EM in Dielettrici ideali
•
Volendo fare un grafico dell’impedenza di ingresso Zi al variare della
frequenza f, essa sarà qualitativamente una funzione di questo tipo:
Zi
λ/4
frisonanza
f
Davide Micheli
Zi
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
312
Propagazione libera:
Schermi per onde piane incidenti
normalmente sulla superficie di un
conduttore
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
313
Onde EM in conduttori reali con perdite
•
Un conduttore reale è un mezzo in cui la corrente di conduzione è molto più
grande della corrente di spostamento: giacché la corrente di spostamento
aumenta con ω, i materiali che sono considerati buoni conduttori (ad esempio
il rame) continuano ad essere considerati tali finchè la conducibilità σ rimane
molto più grande della quantità ωε0.
σ
ε ''=
>> ε '
ωε 0
•
Per un conduttore reale si ha:
•
Esiste dunque una pulsazione ω oltre la quale un materiale non può più essere
considerato un buon conduttore. In tale situazione il termine jk diviene:
⎛
~
σ ⎞
⎟⎟
jk = jω µ ε 0 (ε '− jε ' ') = jω µε 0 ⎜⎜ ε '− j
ωε
0 ⎠
⎝
ma si è supposto che : ε ' << ε ' ' pertanto si ha :
⎛ σ ⎞
~
⎟⎟ = jω
jk ≅ jω µε 0 (− jε ' ') = jω µε 0 ⎜⎜
ωε
j
0 ⎠
⎝
⎛ µσ ⎞
⎛ µσ ⎞
⎟⎟ =
⎜⎜
⎟⎟ = ω − 1⎜⎜
j
ω
j
ω
⎠
⎝
⎠
⎝
j
2
(ωµσ )
2
2j = 1 + j allora :
poiché
(ωµσ ) =
(ωµσ ) =
~
jk ≅
j
~
jk ≅
2
[1 + j ] (π fµσ ) = [1 + j ] (π fµσ )
2
2
2
1
2
j2
Davide Micheli
1
[1 + j ] (ωµσ ) = 1 [1 + j ] (2πfµσ ) =
2
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
314
Onde EM in conduttori reali con perdite
•
Essendo:
1
δ=
= profondità di penetrazione, si ha :
π fµσ
⎧α = δ −1
~
[
1+ j]
jk ≅ [1 + j ] (π fµσ ) =
⇒ ⎨
−1
δ
β
δ
=
⎩
~
1
1
jk = α + jβ = + j
δ
•
•
•
•
δ
⇒ A(z,t) = A0e
~
− jk z
= A0e −αz e − jβz = A0e
1
1
− z −j z
δ
e
δ
L’onda dunque si propaga nel mezzo con velocità di propagazione (1+j)/δ con
α=β ovvero la costante di propagazione coincide con la costante di
attenuazione.
c
ω
La velocità di fase vale:
v f = = ωδ = 2π fδ = 2π δ << c
β
λ0
Ci si accorge facilmente che la costante di penetrazione δ è più piccola di λ0, e
quindi la velocità di fase nei mezzi conduttori è più piccola della velocità della
luce c.
Poiché la velocità di fase cresce con la frequenza allora si è in presenza di
dispersione anomala.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
315
Onde EM in conduttori reali con perdite
•
L’impedenza
d’onda η in un conduttore reale è in tal caso data da:
r
E
µ
µ
≅ [ε ' è trascurabile] =
η= r = ~ =
ε
ε 0 (ε '− jε ' ')
H
η=
µ
ε 0 (− jε ' ')
π fµ
η = (1 + j )
σ
η = (1 + j )RS
⇒ η = (1 + j )RS
•
=
µ
⎛
σ ⎞
⎜
⎟⎟
ε0⎜ − j
⎝ ωε 0 ⎠
=
jωµε 0
ε 0σ
=
jωµ
σ
=
j 2πfµ
σ
= 2j
πfµ
=
σ
π fµ
dove :
= RS (impedenza per quadro)
σ
poiche in un coduttoreσ è grande allora RS è piccolo
r
E
è piccolo e η = r << η0 ≅ 377Ω
H
La moltiplicazione per (1+j) significa che l’impedenza d’onda η ha una parte
reale ed un coefficiente dell’immaginario che coincidono. Inoltre essendo
l’impedenza d’onda pari al rapporto tra campo elettrico e campo magnetico, se
questo rapporto è un numero complesso vuol dire essi che sono sfasati, nel
nostro caso di 45° con E in anticipo rispetto ad H. Se invece il rapporto era un
numero reale allora E ed H sarebbero stati in fase tra loro.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
316
Onde EM in conduttori reali con perdite
•
•
Dunque nei materiali buoni conduttori il rapporto E/H (vettori), è molto più
piccolo di quello che si ha nel vuoto ( da 120π Ω, si arriva ad 1/100 di Ohm);
Inoltre campo elettrico e campo magnetico non sono in fase come in un onda
piana nel vuoto (in un dielettrico ideale), ma sono sfasati di 45°,
sottintendendo naturalmente che E ed H sono perpendicolari tra loro.
∠E= ∠H+45°
•
•
Se il materiale conduttore è usato come schermo allora In funzione del tipo
sorgente che si vuole schermare va scelto il tipo di schermo più appropriato.
Per un onda piana (sorgente lontana), l’onda riflessa è proporzionale al salto
di impedenza η2- η1 come in una linea.
–
–
Per un onda piana il rapporto E/H, che nel vuoto vale circa 377 Ω, scende a
0.014 Ω se c’è il metallo, ed il coefficiente di riflessione è quasi uguale ad 1
ovvero praticamente tutta l’onda viene riflessa.
Per tale motivo se ci si deve proteggere da un’onda che proviene da lontano, non
conviene realizzare grandi schermi: è sufficiente un foglio di alluminio, perché
presenta un’impedenza bassissima, e l’onda che viene da lontano trovando un
salto di impedenza viene quasi completamente riflessa. Lo spessore dello
schermo in questo caso non influisce molto l’importante è che ci sia un salto di
impedenza più grande possibile)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
317
Onde EM in conduttori reali con perdite
•
Per una sorgente di disturbo vicina (sorgente vicina), come per esempio un
Personal Computer, non siamo in condizioni di campo lontano.
–
–
Per tale tipo di sorgente l’unico effetto importante da considerare è l’effetto pelle.
L’effetto pelle presuppone tuttavia schermi grandi (spessore più elevato) e
realizzati con materiali ferromagnetici.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
318
Riflessione da un conduttore reale
•
•
•
Un conduttore ideale riflette tutto. Un conduttore reale invece quanto riflette ?
Il problema è il seguente: si ha un onda che incide su un conduttore con
conducibilità σ ≠ ∞, ad esempio σ= σCu. Si avrà un onda trasmessa ed un onda
riflessa
L’onda trasmessa si attenuerà come exp(-z/δ), dove:
δ = profondità di penetrazione =
1
π fµσ
Atx = attenuazione onda trasmessa = e
−
z
δ
=
1
z
eδ
E(t)
E(i)
E(r)
e
−
z
δ
z
σ Cu≠ ∞
Davide Micheli
1
=
e
z
1
π fµσ
=
1
ez
π fµσ
Si ha un doppio effetto di schermo del
materiale: il primo effetto di schermo da
parte del materiale consiste nel fatto che
l’onda viene parzialmente riflessa; il
secondo effetto consiste nel fatto che
l’onda trasmessa si attenua per effetto
pelle.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
319
Trasmissione dentro un conduttore reale: eff. pelle
•
•
L’attenuazione dell’onda per la parte di riflessione è dovuta alle due superfici
del conduttore; ciascuna superficie rappresenta un salto di impedenza elevato
tra il vuoto ed il metallo. Per tale ragione il maggiore effetto di attenuazione
per un onda piana è dovuto alla riflessione sulle superfici del materiale
metallico.
Per quanto riguarda invece l’attenuazione dovuta a trasmissione nel metallo
ovvero all’effetto pelle, si ha a che fare con un campo elettrico che si propaga
all’interno di un conduttore secondo una legge del tipo:
1
δ = profondità di penetrazione =
π fµσ
−
t
E = E0 e δ e
−j
t
δ
E’
E(0)
z
E(r)
t
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
320
Trasmissione dentro un conduttore reale: eff. pelle
•
•
•
Un onda con campo elettrico E, incide sullo schermo di spessore finito t,
l’onda riemerge dall’altra parte (la si indichi con E’).
Si trascurino per ora i problemi di condizioni al contorno (deve infatti essere
soddisfatta la continuità dei campi, ecc) e si supponga che TUTTA l’onda
incidente venga trasmessa all’interfaccia di spessore t
Il rapporto tra tra E’ ed E viene definito efficienza di schermatura (shielding
effectiveness) e considerando i moduli dei vettori campo elettrico si ha
−
E'
E0e
=
E
E0
•
•
•
t
δ
dove
−
t
E ' = E0 e δ e
−j
t
δ
= E0 e
−
t
δ
Se lo schermo avesse uno spessore infinito non arriverebbe nulla dall’altra
parte.
Nella realtà non ha senso uno spessore infinito: di conseguenza se stiamo
costruendo uno schermo, una parte del campo elettrico incidente oltrepasserà
lo schermo, dando luogo ad un certo disturbo.
Per quantificare l’efficienza di schermatura si utilizza la seguente:
A(dB ) = 20 Log10
⎡
1
⎢
= 20 Log10
⎢ − δt
E'
⎣e
E
Davide Micheli
⎤
⎡ δt ⎤
⎥ = 20 Log10 ⎢e ⎥ = 20 t Log10 [e] = 8,686 ⋅ t
⎥
δ
δ
⎣
⎦
⎦
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
321
Trasmissione dentro un conduttore reale: eff. pelle
•
•
Si stanno trascurando i fenomeni di riflessione presenti nell’interfaccia: l’onda
che arriva viene in parte riflessa, ed in parte trasmessa, per cui in realtà la
porzione che attraversa lo schermo sarà leggermente inferiore all’onda
incidente.
La relazione è lineare con lo spessore t del materiale.
A(dB ) = 8,686 ⋅
•
•
•
t
δ
La relazione in dB è lineare con lo spessore t del materiale.
È ovvio che in termini di numeri naturali, la retta diverrà un esponenziale.
Pertanto all’aumentare dello spessore t del materiale l’efficienza di
attenuazione aumenta esponenzialmente.
Oltre al fenomeno della proporzionalità con t esiste anche la dipendenza dalla
frequenza f:
1
δ=
π fµσ
Davide Micheli
⇒
[
A(dB) = 8,686 t π fµσ
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
]
322
Trasmissione dentro un conduttore reale: eff. pelle
•
L’attenuazione espressa in dB è proporzionale alla radice quadrata della
frequenza f ed alla radice prodotto µσ.
[
A(dB) = 8,686 t π fµσ
•
•
•
]
Analizzando due materiali conduttori come Ferro e Rame ci si accorge che il
Rame ha una conducibilità σ, circa 10 volte superiore al Ferro ma il Rame ha
una permeabilità magnetica µ, circa 1000 volte inferiore rispetto al Ferro.
Pertanto la radice del prodotto µσ per il Ferro è circa 10 volte quella del Rame.
Di conseguenza per l’effetto pelle, uno schermo di rame di 1mm equivale ad
uno schermo ferromagnetico di 1/10 di mm.
In conclusione se si vuole sfruttare maggiormente l’effetto pelle per sorgenti
vicine da schermare, allora conviene utilizzare un materiale ferromangetico,
viceversa se si vuole maggiormente sfruttare la riflessione per schermare
sorgenti lontane, allora conviene utilizzare un materiale maggiormente
conduttore in quanto aumenta il salto di impedenza η e la Resistenza
superficiale o Resistenza quadro Rs del Rame è in tal caso circa 100 volte
inferiore a quella del Ferro
⎡ π fµ ⎤
π fµ
η = (1 + j )⎢
=
dove
Rs
⎥
σ
⎣ σ ⎦
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
323
Trasmissione dentro un conduttore reale: eff. pelle
•
•
Occorre ricordare infine che i materiali non hanno le stesse caratteristiche al
variare della frequenza ed al variare dei campi che li attraversano.
Nel grafico sotto è riportata la permeabilità magnetica relativa µr di un
materiale ferromagnetico al variare della frequenza:
µr
100k
•
Materiale ferromangetico A
Materiale ferromagnetico B
10k
1k
Acciaio tipico
100
10
•
1
f
100
1k
10k
100k
Davide Micheli
La
permeabilità
magnetica
relativa µr di un materiale
ferromagnetico si riduce ad 1
drasticamente
quando
la
frequenza aumenta pertanto al
di sopra di una certa frequenza
tali materiali non sono più
ferromangetici e presentano
una µr =1.
Pertanto all’aumentare della
frequenza le caratteristiche
schermanti di un materiale
ferromagnetico si riducono.
1M
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
324
Trasmissione dentro un conduttore reale: eff. pelle
•
Nel grafico sotto è riportata la permeabilità magnetica relativa µr di un
materiale ferromagnetico al variare dell’intensità del flusso magnetico che lo
attraversa:
µr
•
100k
10k
1k
•
100
Saturazione di µr
10
La
permeabilità
magnetica
relativa µr di un materiale
ferromagnetico si riduce ad 1
drasticamente
quando
la
intensità del flusso magnetico
B aumenta.
Pertanto all’aumentare della
intensità di flusso mangetico B
le caratteristiche schermanti di
un materiale ferromagnetico si
riducono.
1
1
10
100
Davide Micheli
kGaus
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
325
Matrice di diffusione (scattering)
in microonde
Metodi utilizzati nella caratterizzazione dei
materiali sottoposti a microonde
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
326
PARAMETRI S
• Un possibile set di parametri utilizzato per caratterizzare
completamente un quadripolo lineare, come i parametri
h, Z, Y, ABCD, sono i parametri S.
• Tale set di parametri è particolarmente sfruttato nelle
radiofrequenze [ MHz – GHz ], dove non si possono più
usare modelli circuitali a parametri concentrati e gli
stimoli hanno natura ondulatoria. Esistono ovviamente
formule di conversione per passare dai parametri S a
quelli di altro tipo.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
327
Matrice di Scattering o di Diffusione
• La matrice ABCD, risulta comoda per rappresentare la connessione in
cascata. Tuttavia essa non è indicata per descrivere le ampiezze dei
segnali in ingresso ed in uscita. Infatti in alta frequenza, è difficile fare
misure di tensione e di corrente: esiste una difficoltà operativa. Infatti
nella loro misura si dovrebbero inserire i puntali dello strumento, atto
alla misura, i quali, data la frequenza elevata, diverrebbero uno stub che
perturba il sistema e falsa la lettura.
• Viceversa esistono degli analizzatori (analizzatori vettoriali di rete) che
misurano, una volta inviato un segnale unitario, la riflessione e la
trasmissione del segnale, in ampiezza e fase.
• La matrice di scattering è l’unica determinabile con misure dirette di
trasmissione e di riflessione ed è per questo che è molto importante.
Z0 viene assunta, in generale pari a 50 Ω,
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
328
Matrice di Scattering o di Diffusione
• Consideriamo un onda ti tensione (o di campo elettrico trasverso) a1 che entra
alla porta (1) del circuito lineare, e cerchiamo di valutare l’onda riflessa b1 che
esce da questa porta. Analogamente alla porta (2).
a2
a1
(1)
b1
Circuito lineare
tempo-invariante
(2)
b2
• Il circuito deve essere lineare altrimenti non si può definire globalmente la
matrice del circuito. Inoltre la linearità è essenziale per avere una
descrizione del fenomeno indipendentemente dal segnale dal segnale di
ingresso (frequenza).
• Per un circuito non lineare si può ancora definire una matrice, ma solo in un
intorno di un punto (punto di polarizzazione o di lavoro del circuito)
ottenendo dei parametri indipendenti dal segnale.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
329
Matrice di Scattering o di Diffusione
• Nel valutare b1 e b2 (conviene usare le ampiezze di Fourier V(ω)ejωt I(ω)ejωt),
dobbiamo considerare le porte del circuito adattate (cioè con la stessa
impedenza di ingresso). In questo modo l’unica onda che entra nel circuito è
quella della sorgente (e non onde riflesse dal carico). In questo modo si evitano
riflessioni ulteriori che complicherebbero il fenomeno non permettendo di
distinguere il segnale tra parte incidente e parte riflessa.
• La matrice di scattering è così definita:
⎛ b1 ⎞
⎛ a1 ⎞
⎜⎜ ⎟⎟ = S ⋅ ⎜⎜ ⎟⎟
⎝ b2 ⎠
⎝ a2 ⎠
⎛ b1 ⎞ ⎡ S11 S12 ⎤⎛ a1 ⎞
⎜⎜ ⎟⎟ = ⋅⎢
⎜⎜ ⎟⎟
⎥
⎝ b2 ⎠ ⎣S 21 S 22 ⎦⎝ a2 ⎠
⎧ b1 = S11 ⋅ a1 + S12 ⋅ a 2
⎪
⎨
⎪⎩b2 = S 21 ⋅ a1 + S 22 ⋅ a 2
• Dove i parametri S sono complessi.
(1) Z0
a1
a2
a1
Circuito lineare
tempo-invariante
S11
Z0 (2)
b2
b1
S21
b1
b2
S12
S22
a2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
330
Matrice di Scattering o di Diffusione
b
S11 = 1
a1 a2 = 0
• Misura la riflessione alla porta (1) quando alla stessa l’incidenza è
unitaria e non c’è segnale sorgente alla porta (2). La porta (2) è
adattata al carico. (a2=0 non significa quindi corto circuito).
S12 =
b1
a2 a1 = 0
• Misura la trasmissione del segnale dalla porta (2) alla porta (1)
quando la porta (1) è priva di sorgente.
S 21 =
b2
a1 a2 = 0
• Misura la trasmissione del segnale dalla porta (1) alla porta (2)
quando la porta (2) è priva di sorgente.
S 22 =
b2
a 2 a1 = 0
• Misura la riflessione alla porta (2) quando alla stessa l’incidenza è
unitaria e non c’è segnale sorgente alla porta (1). La porta (1) è
adattata al carico. (a1=0 non significa quindi corto circuito).
• S11 e S22 rappresentano dei coefficienti di riflessione
• S12 e S21 rappresentano dei coefficienti di trasmissione
• Essendo i coefficienti S complessi dobbiamo considerare 8 parametri reali, 2 per
ogni coefficiente.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
331
PARAMETRI S
• Dato un generico quadripolo lineare Q
I2
I1
+
V1
-
1
Q
2
+
V2
-
• mettiamo in evidenza le sue due porte e definiamo per ciascuna di esse le
grandezze:
V1 + Z 0 ⋅ I1
⎧
=
a
⎪ 1
2 ⋅ Z0
⎪⎪
Vi + Z 0 ⋅ I i
⎧
⎨
=
a
⎪ i
⎪
V1 − Z 0 ⋅ I1
⋅
2
Z
0
⎪⎪
=
b
⎪ 1
i
=
1
,
2
2 ⋅ Z0
⎪⎩
⎨
⎪
Vi − Z 0 ⋅ I i
=
b
⎪ i
2 ⋅ Z0
⎪⎩
Z0 viene assunta, in generale pari a 50 Ω,
Davide Micheli
V2 + Z 0 ⋅ I 2
⎧
=
a
⎪ 2
2 ⋅ Z0
⎪⎪
⎨
⎪
V − Z0 ⋅ I 2
⎪b2 = 2
2 ⋅ Z0
⎪⎩
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
332
PARAMETRI S
• Ricaviamo Vi e Ii in funzione di ai e bi:
⎧2 ⋅ Z 0 ⋅ ai = Vi + Z 0 ⋅ I i
⎪
⎨
⎪2 ⋅ Z ⋅ b = V − Z ⋅ I
0
i
i
0
i
⎩
• sommando e sottraendo le due precedenti equazioni si ha:
⎧ 2 ⋅ Z 0 ⋅ (ai + bi ) = 2 ⋅ Vi
⎪
⎪
⎨
⎪2 ⋅ 1 ⋅ (ai − bi ) = 2 ⋅ I i
⎪⎩
Z0
• Da cui si trova:
⎧Vi = Z 0 ⋅ (ai + bi )
⎪
⎪
⎨
⎪ I i = 1 ⋅ (ai − bi )
⎪⎩
Z0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
333
PARAMETRI S
• Per passare dalle grandezze ai alle bi , si definiscono i parametri :
⎧ b1 = S11 ⋅ a1 + S12 ⋅ a 2
⎪
⎨
⎪⎩b2 = S 21 ⋅ a1 + S 22 ⋅ a 2
• In forma matriciale:
⎛ a1 ⎞
⎛ b1 ⎞
⎜⎜ ⎟⎟ = S ⋅ ⎜⎜ ⎟⎟
⎝ a2 ⎠
⎝ b2 ⎠
⎛ b1 ⎞ ⎡ S11 S12 ⎤⎛ a1 ⎞
⎜⎜ ⎟⎟ = ⋅⎢
⎜⎜ ⎟⎟
⎥
⎝ b2 ⎠ ⎣S 21 S 22 ⎦⎝ a2 ⎠
• La matrice S caratterizza completamente un quadripolo lineare, così come lo fa
la matrice Z, la Y, la H e la ABCD. Se un quadripolo e reciproco ( le matrici Z e Y
sono simmetriche ) allora anche la matrice S e simmetrica.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
334
APPLICAZIONE DEI PARAMETRI S
• Supponiamo di collegare il quadripolo a due linee di trasmissione con
impedenza caratteristica Z0:
Z0
I1(0)
I2(0)
+
V1(0)
-
+
V2(0)
-
1
Q
2
Z0
• Possiamo scrivere:
⎧ V1 (0) = V1 + + V1 −
⎪
⎪
⎨
+
−
⎪ I (0) = V1 − V1
⎪⎩ 1
Z0 Z0
Davide Micheli
⎧ V2 (0) = V2 + + V2 −
⎪
⎪
⎨
+
−
⎪ I (0) = V2 − V2
⎪⎩ 2
Z0
Z0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
335
APPLICAZIONE DEI PARAMETRI S
• Confrontiamo tali espressioni, con quelle scritte in funzione di ai e bi e :
⎧ V1 (0) = V1 + + V1 −
⎪
⎪
⎨
+
−
V
V
⎪ I (0) = 1 − 1
⎪⎩ 1
Z0 Z0
⎧V1 (0 ) = Z 0 ⋅ (a1 + b1 )
⎪
⎪
⎨
⎪ I 1 (0) = 1 ⋅ (a1 − b1 )
⎪⎩
Z0
⎧ V2 (0) = V2 + + V2 −
⎪
⎪
⎨
+
−
V
V
⎪ I (0) = 2 − 2
⎪⎩ 2
Z0
Z0
⎧V2 (0) = Z 0 ⋅ (a 2 + b2 )
⎪
⎪
⎨
⎪ I 2 (0) = 1 ⋅ (a 2 − b2 )
⎪⎩
Z0
• Confrontando le otto equazioni si ottiene:
⎧V1+ = Z 0 ⋅ a1
⎪
⎨
⎪V − = Z ⋅ b
0
1
⎩ 1
⎧V2+ = Z 0 ⋅ a 2
⎪
⎨
⎪V − = Z ⋅ b
0
2
⎩ 2
• Troviamo dunque le relazioni che legano ai e bi ai fasori delle onde di tensione:
⎧
V1+
⎪a1 =
Z0
⎪
⎪
⎨
⎪
V1−
⎪b1 =
Z0
⎪⎩
Davide Micheli
⎧
V2+
⎪a 2 =
Z0
⎪
⎪
⎨
⎪
V2−
⎪ b2 =
Z0
⎪⎩
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
336
APPLICAZIONE DEI PARAMETRI S
• Confrontiamo tali espressioni, con quelle scritte in funzione di ai e bi e :
⎧ V1 (0) = V1 + + V1 −
⎪
⎪
⎨
+
−
V
V
⎪ I (0) = 1 − 1
⎪⎩ 1
Z0 Z0
⎧V1 (0 ) = Z 0 ⋅ (a1 + b1 )
⎪
⎪
⎨
⎪ I 1 (0) = 1 ⋅ (a1 − b1 )
⎪⎩
Z0
⎧ V2 (0) = V2 + + V2 −
⎪
⎪
⎨
+
−
V
V
⎪ I (0) = 2 − 2
⎪⎩ 2
Z0
Z0
⎧V2 (0) = Z 0 ⋅ (a 2 + b2 )
⎪
⎪
⎨
⎪ I 2 (0) = 1 ⋅ (a 2 − b2 )
⎪⎩
Z0
• Confrontando le otto equazioni si ottiene:
⎧V1+ = Z 0 ⋅ a1
⎪
⎨
⎪V − = Z ⋅ b
0
1
⎩ 1
⎧V2+ = Z 0 ⋅ a 2
⎪
⎨
⎪V − = Z ⋅ b
0
2
⎩ 2
• Troviamo dunque le relazioni che legano ai e bi ai fasori delle onde di tensione:
⎧
V1+
⎪a1 =
Z0
⎪
⎪
⎨
⎪
V1−
⎪b1 =
Z0
⎪⎩
⎧
V2+
⎪a 2 =
Z0
⎪
⎪
⎨
⎪
V2−
⎪ b2 =
Z0
⎪⎩
Davide Micheli
a1 = onda di potenza incidente sulla porta 1
b1 = onda di potenza riflessa sulla porta 1
a 2 = onda di potenza incidente sulla porta 2
b2 = onda di potenza riflessa sulla porta 2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
337
APPLICAZIONE DEI PARAMETRI S
• La potenza che transita sulla linea 1 può essere espressa in funzione di
ai e bi:
2
2
1
1
P1 =
[
⎡V +
1
2 ⋅ Z 0 ⎢⎣
2
− V1− ⎤ = a1 − b1
⎥⎦ 2
2
]= P
IN
che coincide con la potenza entrante nel quadripolo dalla porta 1.
• Analogamente, quella sulla linea 2, può essere espressa come:
1
P2 =
2 ⋅ Z0
⎡V +
⎢⎣ 2
2
−V
− 2
2
[
⎤=1 a 2−b
2
⎥⎦ 2 2
2
] = −P
OUT
• Da queste due formule si ricava una indicazione importante:
• La potenza netta ad una porta è pari alla differenza tra la potenza entrante
ed uscente da quella porta.
• Ecco pertanto una dimostrazione della comodità della matrice S.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
338
APPLICAZIONE DEI PARAMETRI S
• Se si suppone che non vi siano sorgenti né elementi dissipativi all’interno del
sistema allora la potenza si conserva e quindi la differenza tra la potenza che
entra nel circuito e quella che esce (cioè la potenza netta P, appunto) deve
necessariamente essere nulla.
• In termini di matrice di scattering questo significa:
⎧ S 2 + S 2 =1
⎛ S11
⎜⎜
⎝ S 21
S12 ⎞⎛ S11*
⎟⎟⎜⎜ *
S 22 ⎠⎝ S 21
S12* ⎞ ⎛ 1 0 ⎞
⎟ = ⎜⎜
⎟⎟ ⇒
* ⎟
S 22 ⎠ ⎝ 0 1 ⎠
21
⎪ * 11
*
⎪S11S12 + S 21S 22 = 0
⎨ *
*
+
S
S
S
22 S 21 = 0
⎪ 12 11
⎪ S 2 + S 2 =1
22
⎩ 12
• La prima e la quarta relazione hanno u n significato fisico ben preciso.
–
–
Consideriamo lo schema a 2-porte e supponiamo che a1=1 e a2=0 cioè il 2-porte è
privo di sorgente alla porta 2.
Questo implica che S11=b1 e anche che S21=b2 e quindi anche che:
S11 = b1
2
S 21 = b2
2
2
2
che esprime la potenza riflessa alla porta 1
che esprime la potenza trasmessa alla porta 2
essendo la potenza entrante unitaria :
S11 + S 21 = 1
2
2
Davide Micheli
Esprime la conservazione della
potenza alla porta (1). Cioè la
potenza riflessa e trasmessa
sono in somma eguali alla
potenza entrante alla porta (1).
Analogamente
si
ripete
il
ragionamento per la porta 2.
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
339
APPLICAZIONE DEI PARAMETRI S
• Se una matrice S rappresentante un 2-porte è Reciproca allora S12=S21:
–
Ovvero stessi coefficienti di trasmissione alle due porte (1) e (2).
• Se una matrice S rappresentante un 2-porte è Simmetrica allora S12=S21 S11=S22 :
–
–
Ovvero stessi coefficienti di trasmissione alle due porte (1) e (2).
Ovvero stessi coefficienti di riflessione alle due porte (1) e (2).
• È evidente che la reciprocità è deiversa ed è meno forte della simmetria. Nel
caso di simmetria scambiando le due porte di un 2-porte dobbiamo ottenere le
stesse risposte cioè si hanno porte uguali sia in trasmissione che in riflessione.
• Nel caso di materiali privi di ferrite la simmetria fisica implica la simmetria
elettrica.
• Nel caso di transizione Cavo_coax-Guida_d’onda, il circuito è reciproco in
quanto non si hanno materiali girotropici, ma tuttavia non è simmetrico in
quanto S11≠S22:
Z L − Z 0 75 − 50
S11 = ρ1 =
=
Z L + Z 0 75 + 50
50Ω
75Ω
S 22 = ρ 2 =
Davide Micheli
≠
Z L − Z 0 50 − 75
=
Z L + Z 0 50 + 75
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
340
APPLICAZIONE DEI PARAMETRI S
• La matrice S permette dunque di esprimere le onde di potenza riflessa,
sia in ingresso che in uscita (b1 e b2 ), in funzione delle onde di potenza
incidenti in ingresso e in uscita ( a1 e a2).
• Ad esempio:
b2
V2−
S 21 =
= +
a1 a 2 = 0 V1
• è il rapporto tra la potenza riflessa in uscita e la potenza incidente sulla porta
d’ingresso
• Possiamo dunque vedere il quadripolo come in grado di elaborare, tramite i
parametri (S), le onde di potenza che riceve in ingresso alla porta 1 (a1), e alla
porta 2 (a2), combinarle linearmente con i coefficienti (S), in modo da ottenere
due onde di potenza uscenti (b1 e b2), rispettivamente dalla porta 1 e dalla
porta 2.
b1
V1−
S11 =
= +
a1 a 2 = 0 V1
• S11 è il rapporto tra la potenza riflessa dal quadripolo sulla porta 1 e quella che
incide sulla porta stessa
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
341
APPLICAZIONE DEI PARAMETRI S
• La condizione a2=0 equivale a porre V2+Z0I2=0, questo accade
chiudendo la porta 2 su un impedenza Z0:
I2
I1
+
V1
1
Q
-
2
+
V2
-
Z0
• In questo caso si ha infatti V2 = − Z 0 ⋅ I 2
• Dunque per valutare i coefficienti della matrice S è necessario:
• Chiudere la porta 2 su Z0, in modo da trovare S11 ed S21
• Chiudere la porta 1 su Z0, in modo da trovare S12 ed S22
• infatti
S12 =
b1
a 2 a1 = 0
Davide Micheli
S 22 =
b2
a 2 a1 = 0
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
342
Propagazione guidata
Generalità sulle guide d’onda metalliche
Davide Micheli
Eq
di
Maxwell,
Propagazione
Materiali conduttori e dielttrici
radio,
343
Generalità sulle guide d’onda
• Una guida d’onda rettangolare è una scatola a sezione rettangolare,
perfettamente metallica (si considera un metallo conduttore ideale, cioè
σ=∞
• Si assume la direzione di propagazione lungo l’asse z
σ=∞
σ=∞
b
y
z
x
a
• Essendo formata da un solo conduttore non si propagano modi T.E.M.
• Ricordiamo infatti che il numero di modi T.E.M. che si propagano è pari
al numero dei conduttori meno 1 cioè:
n°modi_T.E.M=Ncond-1
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
344
Generalità sulle guide d’onda
• I modi che si possono propagare in una guida d’onda rettangolare sono
solo modi T.E.(Trasversale Elettrico) e modi T.M.(Trasversale
Magnetico).
• La guida d’onda permette la propagazione di questi modi a frequenze
maggiori rispettivamente della frequenza di taglio [fc] caratteristica di
ciascun modo.
• I modi che si propagano non sono altro che le soluzioni dell’equazione
D’onda per i modi T.M. e per i modi T.E. alle quali sono applicate le
condizioni al contorno per i campi elettrici e magnetici sulle faccie
interne conduttrici della guida d’onda.
• La frequenza di taglio per una guida d’onda rettangolare di lati a=2b
risulta essere:
2
2
[ f c ]m.n =
[ f c ]m.n =
1
2π µε
1
2a µε
⎛ mπ ⎞ ⎛ nπ ⎞
⎜
⎟ +⎜
⎟
⎝ a ⎠ ⎝ b ⎠
se a = 2b allora
m 2 + 4n 2
•I modi in propagazione sono identificati dai pedici m,n che sono numeri interi tra 0 e ∞.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
345
Generalità sulle guide d’onda
• I modi in propagazione sono identificati dai pedici m,n che sono numeri
interi tra 0 e ∞.
• Per i modi T.E.m, n i pedici m, n non possono essere
contemporaneamente uguali a zero in quanto questa configurazione
corrisponde a quella di un campo magnetico statico longitudinale che
non si propaga nella guida d’onda.
• Il modo T.E. con frequenza minima che si propaga è quello
corrispondente ad m=1 ed n=0 cioè io modo T.E.10 anche chiamato
modo fondamentale
• Per i modi T.M.m, n i pedici m, n non possno essere uguali a zero.
• Il modo T.M. con frequenza minima che si propaga è quello
corrispondente ad m=1 ed n=1 cioè io modo T.M.11
• Alimentando un tratto di guida d’onda rettangolare di lati a=2b, con un
generatore che parte da frequenza zero, non si propaga nulla fino a che
non si incontra la prima frequenza di taglio, ovvero sia la [fc]m,n del
modo fondamentale con frequenza di taglio più bassa. Salendo in
frequenza, mentre il primo modo continua a propagarsi, partirà il
secondo modo; e cosi via con l’aumentare degli indici m,n.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
346
Generalità sulle guide d’onda
• Il modo T.E.10 è l’unico modo che può propagarsi da solo:
T.E.21
T.M.21
T.E.11
T.M.11
T.E.01
T.E.20
T.E.10
• La guida rettangolare con lati a=2b è una geometrica
che permette di distanziare sufficientemente in
frequenza il modo T.E.1.0 da tutti gli altri modi in
propagazione.
• Dal momento che ogni modo viene disperso in
frequenza, ampiezza, e fase in modo differente, si
comprende come poter propagare un solo modo
semplifica nelle telecomunicazioni il compito di
equalizzare la linea di trasmissione.
fc
1
2
√5
√8
10
1 Modo
0 Modi
[ f c ]T .E .
• Modi in propagazione in una guida d’onda
rettangolare. Ogni modo trasporta una energia.
• In un forno a Microonde a differenza di una linea di
trasmissione, per aumentare ed uniformare la potenza
all’interno della camera riverberante è richiesto che si
propaghino il maggior numero dei modi
3 Modi
5 Modi
∞ Modi
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
347
Generalità sulle guide d’onda
• La frequenza di taglio fondamentale per una guida d’onda rettangolare
di lati a=2b con a variabile da 1 nm a 1 cm risulta essere:
Frequenza di taglio in (Hz) di una guida d'onda rettangolare di lati a=2b al variare della
dimensione di a in (m)
1.60E+17
[ f c ]1.0 =
1.50E+17
1.40E+17
1
dove per una guida cava vuota
2a µε
1
µε
= c = 3 ×108 m/s
1.30E+17
1.20E+17
1.10E+17
fc(Hz) [a=2b]
9.00E+16
8.00E+16
7.00E+16
6.00E+16
5.00E+16
4.00E+16
3.00E+16
Zoom in the next slide
2.00E+16
1.00E+16
1.68E-02
8.39E-03
4.19E-03
2.10E-03
1.05E-03
5.24E-04
2.62E-04
1.31E-04
6.55E-05
3.28E-05
1.64E-05
8.19E-06
4.10E-06
2.05E-06
1.02E-06
5.12E-07
2.56E-07
1.28E-07
6.40E-08
3.20E-08
1.60E-08
8.00E-09
4.00E-09
2.00E-09
0.00E+00
1E-09
fc(Hz)
1.00E+17
lato a (m)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
348
Generalità sulle guide d’onda
• La frequenza di taglio fondamentale per una guida d’onda rettangolare
di lati a=2b con a variabile da 1 cm a 8 cm risulta essere:
Frequenza di taglio in (Hz) per guide rettangolare con llto a=2b dove a varia tra 1 cm e 8 cm
1.60E+10
1.50E+10
1.40E+10
[ f c ]1.0 =
1.30E+10
2a µε
dove per una guida cava vuota
1
µε
= c = 3 ×108 m/s
1.10E+10
1.00E+10
fc(Hz) [a=2b]
9.00E+09
8.00E+09
7.00E+09
6.00E+09
5.00E+09
4.00E+09
3.00E+09
2.00E+09
1.00E+09
1.07E-01
8.92E-02
7.43E-02
6.19E-02
5.16E-02
4.30E-02
3.58E-02
2.99E-02
2.49E-02
2.07E-02
1.73E-02
1.44E-02
1.20E-02
0.00E+00
1.00E-02
Frequenza taglio (Hz)
1.20E+10
1
a(m)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
349
Generalità sulle guide d’onda
• Le velocità di fase vf e la velocità di gruppo vg sono date dalle seguenti
equazioni valide sia per modi T.E. che T.M.
ω
vf = =
β
vg =
1
µε
⎛ fc ⎞
1-⎜⎜ ⎟⎟
⎝ f ⎠
2
m/s
⎛f ⎞
1
dω
1-⎜⎜ c ⎟⎟
=
dβ
µε
⎝ f ⎠
2
m/s
⇒
vf vg =
1
= c2
µε
• Poiché la frequenza di taglio dipende dal modo che si sta propagando
ne consegue che ogni modo avrà una propria vf e vg. Ogni modo ha cioè
una propria curva di dispersione ω=ω(β).
• Formalmente tutte le velocità di fase sono uguali però graficamente ogni
diagramma vf=vf(f), è traslato rispetto agli altri, ed ha l’asintoto per f=fc,
dove la frequenza di taglio fc varia da modo a modo.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
350
Generalità sulle guide d’onda
vf
T.E.11
T.M.11
T.E.10
T.E.01
T.E.20
1
2
√5
c=
1 Modo
0 Modi
1
µε
3 Modi
5 Modi
Dispersione di una guida d’onda:
(variazione di vf) in funzione della frequenza.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
fc
[ f c ]T .E.
10
351
Generalità sulle guide d’onda
• Nei sistemi di telecomunicazione le guide d’onda, pur essendo
dispersive, possono essere utilizzate sono nell’intervallo di frequenze
fra quella di taglio del modo fondamentale e quella del primo modo
superiore, che in questo caso particolare è il modo T.E.01 e T.E.20.
• Per f tale che:
fc T .E. = fc T .E. < f < fc T .E. = fc T .M .
01
20
11
11
• Il sistema è anche se dispersivo, perfettamente definito, quindi può
essere equalizzato in ricezione, ritardando le componenti spettrali che
hanno viaggiato più velocemente.
• Quando le curve di dispersione alla stessa frequenza sono 2,3,4,…n,
evidentemente questo non è più possibile.
• Per le telecomunicazioni in genere viene consigliato di utilizzare la guida
d’onda ad un 15÷20% di frequenza al di là della frequenza di taglio.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
352
Generalità sulle guide d’onda
• Per f tale che:
f > f c T .E . = f c T .M .
11
11
• Le guide d’onda possono essere usate se si deve trasportare energia,
potenza, e NON segnali: anzi, se si usa un forno a microonde più modi si
hanno e meglio è, perché ogni modo ha una distribuzione diversa di
campo elettrico, e quindi dissiperà massima potenza dove il campo
elettrico è massimo per cui con pochi modi il forno a microonde
riscalderà in maniera disuniforme: più modi si hanno, più il campo
elettrico tende ad essere uniforme.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
353
Generalità sulle guide d’onda
• Le impedenze modali ZT.E. e ZT.M. a differenza di una linea di
trasmissione dipendono da: Frequenza, Frequenza di taglio, dimensione
e dielettrico:
L
µ
(Linee di Trasmissione)
ZT .E .M . = η
=η
C
ε
ZT .E . =
η
⎡f ⎤
1− ⎢ c ⎥
⎣f ⎦
2
=
Et
Ht
(G.Onda, t sta per componente trasversa)
2
⎡ fc ⎤
Et
ZT .M . = η 1 − ⎢ ⎥ =
Ht
⎣f ⎦
(G.Onda, t sta per componente trasversa)
• In generale per le guide d’onda (cioè propagazione guidata), per ogni
modo (si lavora solitamente con il T.E.10) si può definire una linea di
trasmissione equivalente, e quindi si possono utilizzare tutti i concetti
studiati per le linee di trasmissione, a condizione di ricordare che la
lunghezza d’onda in guida λg è diversa dalla lunghezza d’onda nel
vuoto: λ0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
354
Generalità sulle guide d’onda
• La lunghezza d’onda in guida e la costante di propagazione in guida
sono definite nel modo seguente:
1
λg =
βg =
vf
f
2π
λg
=
=
1
f
µε
⎡ fc ⎤
1− ⎢ ⎥
⎣f ⎦
2π
=
λ0
⎡f ⎤
1− ⎢ c ⎥
⎣f ⎦
2
=
1
f
2π
λ0
c
⎡ fc ⎤
1− ⎢ ⎥
⎣f ⎦
2
2
=
λ0
⎡ fc ⎤
1− ⎢ ⎥
⎣f ⎦
(lunghezza d' onda in guida)
2
⎡f ⎤
⎡f ⎤
1 − ⎢ c ⎥ = β0 1 − ⎢ c ⎥
⎣f ⎦
⎣f ⎦
2
(costante di propagazione in guida d' onda)
2
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
355
Generalità sulle guide d’onda
• Per analogia con le linee di trasmissione supponendo di lavorare con
due tratti di guida d’onda differente denominati 1 e 2, possiamo trovare il
coefficiente di riflessione sull’interfaccia di separazione z=0:
V - Z 2 − Z1
ρ= + =
V
Z 2 + Z1
(coefficiente riflessione per Linea di trasmissione)
E (tr ) ZT .E .2 − ZT .E .1
ρ = (i ) =
Et
ZT .E .2 + ZT .E .1
(coefficiente riflessione per guida d' onda)
1
2
z=0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
356
Generalità sulle guide d’onda
• Un problema classico è considerare una guida d’onda così suddivisa:
una parte 1 è in aria, ed una altra parte 3 contiene un certo dielettrico; si
vuole fare l’adattamento in λ/4:
1
2
3
λg/4
Z 2 = Z1 ⋅ Z 3
• La lunghezza del pezzo 2 è λg/4 calcolato in guida, cioè λg2/4
• L’impedenza modale della guida 2 deve essere la radice quadrata del
prodotto fra l’impedenza modale del mezzo 1 e l’impedenza modale del
mezzo 3. si usa la ZT.E. o la ZT.M. a seconda del modo che sista
considerando
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
357
For a TEM wave guided by a transmission line,
1⎛
C
L⎞
⎟
+G
α ≈ ⎜⎜ R
2⎝
L
C ⎟⎠
(low-loss line)
1 πfµ c
R
=
R=
πa πa σ c
(2-wire line)
∴ α is proportional to f .
The attenuation may be prohibitively high in the microwave
frequencies.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
358
Consider waves propagating along straight guiding structures
with a uniform cross section
General Behaviors
Phasor: v
v
E ( x, y, z ) = E ( x, y )e −γz
v
2
v
∂ E
2
v
=γ E
2
∂z
E
v
v
∂2H
2
& 2 =γ H
∂z
Homogeneous Helmholtz’s equations:
v
v
2
∇ E+k E =0
v
v
2
2
∇ H +k H =0
2
Davide Micheli
(k = ω
µε )
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
359
Consider in rectangular coordinates:
v
v
2
∇ E+k E =0
2
v
⎛ ∂2
∂2
∂2
2⎞
⇒ ⎜⎜ 2 + 2 + 2 + k ⎟⎟ E = 0
∂y
∂z
⎝ ∂x
⎠
v
⎛ 2
∂2
2⎞
⇒ ⎜⎜ ∇ xy + 2 + k ⎟⎟ E = 0
∂z
⎝
⎠
v
2
2
2
⇒ ∇ xy + γ + k E = 0
v
v
2
2
2
(1a)
⇒ ∇ xy E + γ + k E = 0
(
(
Similarly,
(
)
)
)
v
v
2
2
∇ H + γ +k H =0
2
xy
Davide Micheli
(1b)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
360
Interrelationships of the 6 field components
v
v
∇ × E = − jωµH
From
xˆ
∂
∂x
Ex
yˆ
∂
∂y
Ey
zˆ
v
∂
= − jωµH
∂z
Ez
∂E z
∂E z ∂E y
+ γE y = − jωµH x
= − jωµH x ⇒
−
∂y
∂y ∂z
∂E x ∂E z
∂E z
= − jωµH y
= − jωµH y ⇒ −γE x −
−
∂x
∂z ∂x
∂E y ∂E x
∂E y ∂E x
= − jωµH z
−
= − jωµH z ⇒
−
∂x ∂y
∂x ∂y
Davide Micheli
(2a)
(2b)
(2c)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
361
v
v
Similarly, from ∇ × H = jωεE ,we have
∂H z
+ γH y = jωεE x
∂y
∂H z
= jωεE y
− γH x −
∂x
∂H y ∂H x
−
= jωεE z
∂x
∂y
We have
∂E z ⎞
1 ⎛ ∂H z
⎜
⎟⎟
−
j
γ
ωε
2
2 ⎜
∂y ⎠
γ +k ⎝ ∂x
1 ⎛ ∂H z
∂E z ⎞
⎜
⎟⎟
+
Hy = − 2
j
γ
ωε
2 ⎜
∂x ⎠
γ +k ⎝ ∂y
Hx = −
1 ⎛ ∂E z
∂H z ⎞
⎜γ
⎟⎟
+ jωµ
Ex = − 2
2 ⎜
∂y ⎠
γ +k ⎝ ∂x
1 ⎛ ∂E z
∂H z ⎞
⎜γ
⎟⎟
− jωµ
Ey = − 2
2 ⎜
∂x ⎠
γ +k ⎝ ∂y
Davide Micheli
(3a)
(3b)
(3c)
(4a)
(4b)
(4c)
(4d)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
362
Hence, we can solve the scalar Helmholtz’s equations for
Ez and Hz, and use the above formulas to determine other
components.
Propagating waves in a uniform waveguide divide into 3 types
according to whether Ez or Hz exists.
1. Transverse electromagnetics (TEM) waves
Ez = 0 and Hz = 0
2. Transverse magnetic (TM) waves
Ez ≠ 0 and Hz =0
3. Transverse electric (TE) waves
Ez = 0 and Hz ≠0
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
363
Three types of propagating waves:
(1) Transverse electromagnetic (TEM) waves:
Ez = Hz = 0
From (4), for the existence of non-trivial solutions,
2
+ k2 = 0
γ TEM
∴γ TEM = jk = jω µε
∴ u p (TEM ) =
Define,
ω
k
=
1
µε
wave impedance
Z TEM =
(from (3a) & (2b))
Davide Micheli
=
Ex
Hy
jωµ
γ
γ
µ
=
=
=η
ε
jωε
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
(5a)
364
[from (2a)]
jωµ
µ
=−
= − ZTEM
=−
Hx
ε
γ
Ey
(5b)
Notes :
1. the wave impedance is the same as the intrinsic
impedance of the dielectric medium.
2. The phase velocity and wave impedance for TEM
waves are independent of frequency of the wave
Combining (5a) & (5b),
Ey
Ex
H x ˆx + H y ˆy = −
ˆx +
ˆy
ZTEM
ZTEM
v
H=
Davide Micheli
1
ZTEM
v
ˆz × E
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
365
Single conductor hollow (or dielectric filled) waveguides of any
shape cannot support TEM waves.
Reason :
If a TEM wave were
to exist in a
v
waveguide, the H field lines would
form closed loops in a transverse plane.
v v
⇒ ∫ H ⋅dl ≠ 0
c
v
v
v
∗
∗∗
Q J z = 0 & E z = 0 ⇒ Dz = 0
v
⎛ v ∂D ⎞ v
⎟⎟ ⋅ d s = 0
∴ ∫ ⎜⎜ J +
s
∂t ⎠
⎝
Contradiction to Ampere’s Law !!
Waveguide
v
H
* No inner conductor ⇒ no longitudinal conduction current (Jz = 0)
** TEM wave, Ez =0 ⇒no longitudinal displacement current (Dz= 0)
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
366
(2) Transverse Magnetic (TM) Waves:
Hz = 0
(
)
∴ ∇ 2xy E z + γ 2 + k 2 E z = 0
γ
∂E z
Ex = − 2
Form (4):
γ + k2 ∂ x
γ
∂E z
Ey = − 2
γ + k2 ∂ y
jωε ∂E z
Hx = 2
γ + k2 ∂ y
jωε ∂E z
Hy = − 2
γ + k2 ∂ x
γ ⎛ ∂
∂ ⎞
+ ˆy ⎟E z
∴ E x ˆx + E y ˆy = − 2
⎜ ˆx
2
∂ y⎠
γ +k ⎝ ∂x
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
367
i.e.
v
ET = −
Wave impedance :
γ
∇ E
2
2 T z
γ +k
Z TM
Ex
γ
jωµ
=
=
≠
H y jωε
γ
(Qγ
Ey
Hx
TM
≠ γ TEM = jω µε
)
= − Z TM
Ey
Ex
H x ˆx + H y ˆy = −
ˆx +
ˆy
ZTM
ZTM
v
v
1
∴H =
zˆ × E
Z TM
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
368
After solving the Helmholtz equation subject to the
boundary conditions of a waveguide, we will have discrete
values of hmn where:
2
hmn
= γ 2 + k2
( eigenvalue problem)
2
γ = hmn
− k2
2
= hmn
− ω 2 µε
Each eigenvalues of hmn determines the
characteristic properties of a particular TM mode
of the given waveguide.
2
ω c2 µε = hmn
Define :
∴ fc =
Davide Micheli
hmn
2π µε
cutoff frequency
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
369
h mn
ωc =
µε
: angular cutoff frequency
2
− k2
γ = hmn
2
ω
2
= hmn
− ω c2 µε 2
ωc
⎛ f ⎞
= hmn 1 − ⎜⎜ ⎟⎟
⎝ fc ⎠
2
2
<
h
ω
µε
Note γ = jβ, if
mn
hmn
∴ω >
µε
f >
Davide Micheli
2
hmn
2π µε
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
370
(i) For f > fc
γ = jβ = j k − h
2
2
mn
⎛ fc ⎞
= jk 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
⎛ fc ⎞
∴ β = k 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
Guide wavelength:
λg =
=
Davide Micheli
⎛ 2πf c µε ⎞
⎟
= jk 1 − ⎜
⎜ 2πf µε ⎟
⎠
⎝
2
2
2π
( from βz=2π )
β
2π
⎛ fc ⎞
k 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
371
∴ λg =
where
λ
⎛ fc ⎞
1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
>λ
2π
1
u
λ=
=
=
k f µε f
(*)
⎛
1 ⎞
⎜u =
⎟
µε ⎠
⎝
λ is the wavelength of a plane wave with a frequency f.
From (*):
λ2g
=
λ2
2
⎛λ⎞
1 − ⎜⎜ ⎟⎟
⎝ λc ⎠
2
⎛λ⎞
λ2
∴1 − ⎜⎜ ⎟⎟ = 2
λg
⎝ λc ⎠
Davide Micheli
⎛
u ⎞ cutoff
⎜⎜ λ c = ⎟⎟
f c ⎠ wavelength
⎝
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
372
1 1
1
− 2 = 2
2
λ λc λg
1
1
1
= 2 + 2
2
λ λg λc
Phase velocity:
ω
up = =
β
=
=
ω
⎛f ⎞
k 1 − ⎜⎜ c ⎟⎟
⎝ f ⎠
2
ω
⎛ fc ⎞
ω µε 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
λg
=
u >u
2
λ
⎛ fc ⎞
u
1 − ⎜⎜ ⎟⎟
⎝ f ⎠
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
373
∴ The phase velocity within a waveguide is frequency
dependent. i.e. single-conductor waveguides are
dispersive ⇒ narrow BW, low loss
*
Compare with 2-wire transmission line (frequency
independent) ⇒ non-dispersive, more BW, high loss
Group velocity
ug =
1
dβ
dω
2
⎛ fc ⎞
λ
= u 1 − ⎜⎜ ⎟⎟ =
u<u
λg
⎝ f ⎠
note:
u pug = u 2
* In a lossless waveguide, the velocity of signal propagation
is equal to the group velocity.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
374
Z TM
⎛ fc ⎞
jk
γ
=
=
1 − ⎜⎜ ⎟⎟
jωε jωε
⎝ f ⎠
⎛ fc ⎞
µ
=
1 − ⎜⎜ ⎟⎟
ε
⎝ f ⎠
⎛ fc ⎞
= η 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
2
2
2
1. The wave impedance of propagating TM modes in
waveguide with a lossless dielectric is purely
resistive
2. ZTM is always less than the intrinsic impedance of
the dielectric medium
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
375
γ = α = hmn
(II) For f < f c
= hmn
k2
1− 2
hmn
⎛ f ⎞
1 − ⎜⎜ ⎟⎟
⎝ fc ⎠
2
The wave diminishes rapidly with z (evanescent)
⇒Waveguide exhibits the property of a high-pass filter
v
E
⇒Only wave with f > fc can propagate in the guide
ZTM
Note:
⎛f ⎞
γ
h mn
=
1 − ⎜⎜ ⎟⎟
= −j
jωε
ωε
⎝ fc ⎠
2
1. Purely Reactive ⇒ no power flow associated
with evanescent waves.
2. When f ≈ fc, then E << H as (E/H→0)
⇒ energy stored in H-field in waveguide
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
376
(3) Transverse Electric (TE) Waves:
Ez = 0
(
)
∴ ∇ 2xy H z + γ 2 + k 2 H z = 0
jωµ ∂H z
Ex = − 2
γ + k2 ∂ y
jωµ ∂H z
Ey = 2
γ + k2 ∂ x
∂H z
γ
Hx = − 2
γ + k2 ∂ x
γ
∂H z
Hy = − 2
γ + k2 ∂ y
∂ ⎞
γ ⎛ ∂
∴ H x ˆx + H y ˆy = − 2
ˆy ⎟H z
⎜ ˆx +
2 ∂x
∂y ⎠
γ +k ⎝
v
γ
HT = − 2
∇ H
2 T z
γ +k
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
377
E x jωµ
ZTE =
=
Hy
γ
v
v
∴ E T = − ZTE ˆz × H T
Define
A) For f > f c
2
⎛ fc ⎞
γ = jβ = jk 1 − ⎜ ⎟
µ
⎝f ⎠
jωµ
jωµ
ε
=
=
ZTE =
2
2
γ
f
f
⎛ ⎞
⎛ ⎞
jω µε 1 − ⎜ c ⎟
1− ⎜ c ⎟
⎝f ⎠
⎝f ⎠
η
=
2
f
⎛ ⎞
1− ⎜ c ⎟
⎝f ⎠
⇒ Purely resistive and larger than the intrinsic
impedance of the dielectric medium
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
378
B) For f < f c
Z TE =
γ = α = h mn
jωµ
γ
= j
hmn
To summarize, for f > f c
ZTEM
µ
=η=
ε
λ TEM
u
=λ=
f
ZTM
⎛ f ⎞
1 − ⎜⎜ ⎟⎟
⎝ fc ⎠
⎛ fc ⎞
= η 1− ⎜ ⎟
⎝f ⎠
λ TM =
Davide Micheli
⎛f ⎞
1 − ⎜⎜ ⎟⎟
⎝ fc ⎠
ωµ
2
λ
⎛ fc ⎞
1− ⎜ ⎟
⎝f ⎠
2
2
⇒ Energy stored in
E-field in waveguide
2
ZTE =
λ TE =
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
η
⎛ fc ⎞
1− ⎜ ⎟
⎝f ⎠
λ
2
⎛ fc ⎞
1− ⎜ ⎟
⎝f ⎠
2
379
ω-β diagram ( for propagating modes )
ω
slopeTEM
ω
1
= =u =
= velocity
β
µε
TE, TM
ωc
P
ug
ω=
TEM
up
βu
⎛ω ⎞
1 − ⎜⎜ ⎟⎟
⎝ ωc ⎠
2
: for TE, TM
β
Notes :
1.
When operating frequency increases much above the cutoff
frequency, up and ug approach u asymptotically
2.
At point P is the group velocity, ug and ugup=u2 holds
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
380
(1) Rectangular Waveguides
TM waves
E z (x , y , z ) = E z (x , y )e
y
− γz
b
2
⎞
⎛ ∂2
∂
a
2
⎜
⎟
⎜ ∂ x 2 + ∂ y 2 + h ⎟E z (x , y ) = 0
⎠
⎝
By method of separation of variable, let
x
z
E z (x , y ) = X(x )Y( y )
1 d2 X 1 d2 Y
2
−
=
+
h
X dx 2 Y d y 2
function of x only
function of y only
∴ both sides must equal a constant in order for the
equation to hold for all values of x and y.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
381
hence
d2X
2
+
k
xX =0
2
dx
d 2Y
2
+
k
yY = 0
2
dy
k y2 = h 2 − k x2
(
)
d 2Y
2
2
+
h
−
k
x Y =0
2
dy
Boundary conditions:
E z (0, y ) = 0
E z (a, y ) = 0
E z ( x,0) = 0
E z ( x, b ) = 0
Davide Micheli
(1)
(2)
(3)
(4)
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
382
∴X(x) = C1 sinkx x +C2 coskx x
From B.C. (1), C2 = 0
From B.C. (2), sinkxa=0 ⇒ kx=mπ/a
mπ
with k x =
(m=,1,2,3, …….)
∴ X(x ) = sin k x x
a
Similarly,
nπ
Y( y ) = sin k y y
(n=,1,2,3, …….)
with k y =
b
⎛ mπx ⎞ ⎛ nπy ⎞
E z ( x, y ) = Eo sin ⎜
⎟ sin ⎜
⎟
⎝ a ⎠ ⎝ b ⎠
h 2 = k x2 + k y2
⎛ mπ ⎞ ⎛ nπ ⎞
⇒ h2 = ⎜
⎟ +⎜
⎟
⎝ a ⎠ ⎝ b ⎠
2
Davide Micheli
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
383
γ ⎛ mπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
E x ( x, y ) = − 2 ⎜
⎟ Eo cos⎜
⎟ sin ⎜
⎟
h ⎝ a ⎠
⎝ a ⎠ ⎝ b ⎠
γ ⎛ nπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
E y ( x, y ) = − 2 ⎜
⎟ Eo sin ⎜
⎟ cos⎜
⎟
h ⎝ b ⎠
⎝ a ⎠ ⎝ b ⎠
jωε ⎛ nπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
H x ( x, y ) = 2 ⎜
⎟
⎟ Eo sin ⎜
⎟ cos⎜
h ⎝ b ⎠
⎝ a ⎠ ⎝ b ⎠
jωε ⎛ mπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
H y ( x, y ) = − 2 ⎜
⎟ Eo cos⎜
⎟ sin ⎜
⎟
h ⎝ a ⎠
⎝ a ⎠ ⎝ b ⎠
2
⎛ mπ ⎞ ⎛ nπ ⎞
γ = jβ = j ω µε − ⎜
⎟ −⎜ ⎟
⎝ a ⎠ ⎝ b ⎠
2
2
Every combination of the integers m and n defines a
possible mode that may be designated as the TMmn mode.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
384
Notes :
1. There are infinite combination of m and n
2. m define the variation in x-direction (m≠0)
3. n define the variation in y-direction (n≠0)
Cutoff frequency : ( f c )mn =
Cutoff wavelength : (λc )mn =
⎛ mπ ⎞ ⎛ nπ ⎞
⎜
⎟ +⎜
⎟
⎝ a ⎠ ⎝ b ⎠
2
1
2π µε
2
(Hz)
2
2
⎛m⎞ ⎛n⎞
⎜ ⎟ +⎜ ⎟
⎝ a ⎠ ⎝b⎠
2
(m)
TM11 modes has the lowest cutoff frequency of all TM
modes
H
b
E
a
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
385
TE waves
Ez = 0
(∇
H z ( x, y, z ) = H z ( x, y )e −γz
2
xy
Boundary condition:
Ey
x =0
=0
=0
Ey
x =a
Ex
y =0
=0
y=b
=0
Ex
)
+ h 2 H z ( x, y ) = 0
Davide Micheli
∂H z
∂x
∂H z
∂x
∂H z
∂y
∂H z
∂y
=0
x =0
=0
x =a
=0
y =0
=0
y=b
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
386
⎛ mπx ⎞ ⎛ nπy ⎞
∴ H z (x , y ) = H o cos⎜
⎟ cos⎜
⎟
⎝ a ⎠ ⎝ b ⎠
2
⎛ nπ ⎞
2 ⎛ mπ ⎞
h =⎜
⎟ +⎜ ⎟
⎝ a ⎠ ⎝ b ⎠
m=0,1,2,….
n=0,1,2,….
2
jωµ ⎛ nπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
E x (x , y ) = 2 ⎜ ⎟H o cos⎜
⎟ sin⎜
⎟
⎝ a ⎠ ⎝ b ⎠
h ⎝ b ⎠
jωµ ⎛ mπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
E y (x , y ) = − 2 ⎜
⎟H o sin⎜
⎟ cos⎜
⎟
⎝ a ⎠ ⎝ b ⎠
h ⎝ a ⎠
γ ⎛ mπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
H x (x , y ) = 2 ⎜
⎟H o sin⎜
⎟ cos⎜
⎟
⎝ a ⎠ ⎝ b ⎠
h ⎝ a ⎠
γ ⎛ nπ ⎞
⎛ mπx ⎞ ⎛ nπy ⎞
H y (x , y ) = 2 ⎜ ⎟H o cos⎜
⎟ sin⎜
⎟
⎝ a ⎠ ⎝ b ⎠
h ⎝ b ⎠
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
387
( f c )mn =
1
2π µε
⎛ mπ ⎞ ⎛ nπ ⎞
⎟
⎜
⎟ +⎜
a
b
⎠
⎝
⎠ ⎝
2
2
If a>b, f c is the lowest when m=1 & n=0:
1
v
( f c )TE =
=
2a µε 2a
10
(λc )TE
10
= 2a
∴ TE10 mode is the dominant mode of a rectangular
waveguide with a > b
linearly
polarized
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
388
Surface current on guide
wall for TE10 mode.
E & H field for
TE10 mode.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
389
Attenuation
Assume the transverse field patterns are not appreciably
affected by the losses.
⎛σ ⎞
⎟⎟
ε d = ε + ⎜⎜
Dielectric loss
⎝ jω ⎠
ση
αd =
2
⎛ fc ⎞
2 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
Wall loss (metallic loss)
P(z ) = ∫
b
0
for TE10 mode:
∫
a
0
1
− E y H x* dxdy
2
1
⎛ a ⎞ 2 b a 2 ⎛ πx ⎞
= ωµβ ⎜ ⎟ H o ∫ ∫ sin ⎜ ⎟ dxdy
0 0
2
⎝π ⎠
⎝ a⎠
2
⎛ aH o ⎞
= ωµβab⎜
⎟
⎝ 2π ⎠
Davide Micheli
2
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
390
PL ( z ) = 2[P L ( z )]x =0 + 2[P L ( z )]y =0
⎡ a ⎛ f ⎞2 ⎤
2
⎜
⎟
⎢
⎥
= b + ⎜ ⎟ H o Rs
⎢⎣ 2 ⎝ f c ⎠ ⎥⎦
⎛ fc ⎞
β = ω µε 1 − ⎜⎜ ⎟⎟
⎝ f ⎠
(α c )TE
10
=
2
PL ( z )
2 P( z )
( )
⎡ 2b ⎛ f c ⎞ 2 ⎤
Rs ⎢1 +
a ⎜⎝ f ⎟⎠ ⎥
⎦
= ⎣
2
ηb 1 − ⎛⎜ f c f ⎞⎟
⎝
⎠
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
391
∴ (α c )TE10
2
⎡
πfµ c
1
2b ⎛ f c ⎞ ⎤
=
⎢1 + ⎜⎜ ⎟⎟ ⎥
2
a ⎝ f ⎠ ⎥
ηb
⎡ ⎛ f c ⎞ ⎤ ⎢⎣
⎦
σ c ⎢1 − ⎜ f ⎟ ⎥
⎠ ⎦
⎣ ⎝
α c → ∞ when f → f c
αc
fc
f
For a given dimension a, α ↓ as b ↑
But as b↑ , (fc)TE11 ↓ or (fc)TM11 ↓
⇒ BW ↓
The usual compromise is b/a ≈ 1/2.
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
392
TE 01
b/a=1/2
TE10
TE 20
↓
↓
1
2
TE 01
TE10
b/a=1
↓
TE11
TM11
↓
TE11
TM11
10
3
TE 02
TE 20
↓
f c / (f c )TE
10
2
1
a
a
b
f c / (f c )TE
↓
v
E
b
v
E
v
E
TE20
TE10
Davide Micheli
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
393
(2) Circular Waveguides
TM modes:
where
⎧cos nφ
E z = J n (hr )⎨
⎩sin nφ
J n (ha ) = 0
h=
TE modes:
where
ρ nl
a
e.g. ρ01 = 2.405
⎧cos nφ
H z = J n (hr )⎨
⎩sin nφ
J n′ (ha ) = 0
h=
Davide Micheli
ρ nl′
a
e.g. ρ'11 = 1.84
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
394
Cutoff frequency :
( f c )TM
mn
= ( f c )TM mn
=
=
∴
hmn
2π µε
hmn
a µε
TE11 mode has the lowest cutoff frequency
(dominant mode) in a circular waveguide.
TM 01
α
TE 01
TE11
E
H
f c ,11
Davide Micheli
f
Eq di Maxwell, Propagazione libera, materiali
conduttori e dielttrici
395