Lezione introduttiva: onde guidate - Dipartimento di Ingegneria dell

Microonde
Prof. Marco Farina
Dipartimento di Elettromagnetismo e Bioingegneria
Modalità Esami
Prova scritta
Prova orale
Esame di medio termine o Parziale
Testi consigliati
Microwave Engineering, David M. Pozar, Wiley &
Sons;
Ramo-Whinnery-Van Duzer: Campi e Onde
nell’elettronica delle Telecomunicazioni
Microwave Solid State Circuit Design, Inder Bahl e
Prakash Bhartia, Wiley & Sons
Equazioni di Maxwell
 
  
 E  d l   t S B  nds

 
E   B
t

D  
 

 
 D   ds D  n  Q
S
   
H  J  D
t
 
  
 H  d l  I  t S D  nds


 
 B   ds B  n  0
S


B  0
+

  
F  q E  vB

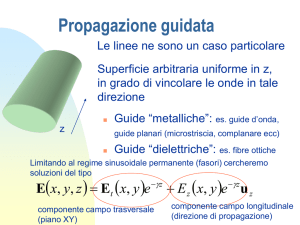
Propagazione guidata
Le linee ne sono un caso particolare
Superficie arbitraria uniforme in z,
in grado di vincolare le onde in tale
direzione

z
Guide “metalliche”: es. guide d’onda,
guide planari (microstriscia, complanare ecc)

Guide “dielettriche”: es. fibre ottiche
Limitando al regime sinusoidale permanente (fasori) cercheremo
soluzioni del tipo
z
 z
t
z
z
Ex, y, z   E x, y e
componente campo trasversale
(piano XY)
 E x, y e u
componente campo longitudinale
(direzione di propagazione)
La costante di propagazione  sarà generalmente complessa
ajb
Cosa si può dedurre dalle equazioni di Maxwell? Mettiamoci in
condizioni di assenza di sorgenti
J  0   0  E z E y

  j H x

Ed esplicitiamo la legge di Faraday
z
 y
 E x E z
  E   jH

  j H y


x
 z
Chiaramente ora
 
z
 E y  E x   j H
z
 x
 E z
y
 E   j H

y
x
 y

E z

  j H y
 E x 
x

 E y  E x   j H
z
 x
y

Analogamente dalla legge di
Ampère/Maxwell
  H  jE
 E z
 y  E y   j H x

E z

  j H y
 E x 
x

 E y  E x   j H
z
 x

y

 H z
 y  H y  j E x

H z

 j E y
  H x 
x

 H y  H x   j E
z
 x

y


1

1   2

Ex 
Hy 
yHz
Hy  

Hy 
 y H z   x Ez 
j
j

j  j
j

j j   2   k 2
    
 x Ez 



H y 1  2  
 H 
2 y z
 k 
j 

 k
1
Hy   2
 y H z  j  x E z
2
 k
 k2  2   
 x Ez

Hy

H

 k 2    k 2 y z j

 
2


Notate che Hy dipende solo
da Hz ed Ez



In modo analogo si ottengono le relazioni
Ex  
Ey 
Hx 
1
2 k
1
 k
2
2
 x E z  j  y H z 
2
  y E z  j  x H z 
1
 k
Hy  
2
2
  x H z  j  y E z 
1
 k
2
2
 y H z  j  x E z 
Cioè: le componenti
trasversali del campo,
nell’ipotesi di onde
guidate, sono funzione
delle componenti
longitudinali
Ora, qualora vi fosse solo propagazione
senza attenuazione
  jb   2  b 2
Ex  
Ey 
1
k b
1
2
k2  b 2
1
2
 x E z  j  y H z 
  y E z  j  x H z 

  x H z  j  y E z
k2  b 2
1
Hy   2
 y H z  j  x E z
k b2
Hx 

così che a denominatore delle relazioni compare k2-b2
Notate che se k=b i campi trasversali divergono a meno che
Ez ed Hz non siano simultaneamente nulle: solo le onde con
Ez=Hz=0, definiti “modi TEM, trasverso-elettromagnetici”,
possono avere costante di propagazione - e quindi velocità
di fase- coincidenti con quelle della luce


Cosa succede all’equazione di Helmhotlz
 2E  k 2E  0
nell’ipotesi di onda guidata ?
Ex, y, z   Ex, y ez

Conviene isolare nell’operatore laplaciano la derivata in z,
cioè scrivere
2 
2
x 2

2
y 2

2
z 2

 t 2 
2
z 2



Il primo termine, che opera solo sulle coordinate x,y,
trasversali rispetto alla direzione di propagazione z, lo
chiamiamo brevemente laplaciano trasverso
D’altro canto la doppia derivazione in z, con la dipendenza
esponenziale che abbiamo assunto, diventa solo una
moltiplicazione per 2 (meraviglie degli esponenziali!)
L’equazione d’onda diventa in tal caso


t 2E  k 2   2 E  0

Che definiremo equazione d’onda per onde guidate;
analogamente per il campo magnetico


t H  k 2   2 H  0
2




Ciascuna eq d’onda vettoriale rappresenta 3 equazioni
scalari
Tuttavia sappiamo che bastano Ez ed Hz per determinare
le altre componenti
Le equazioni di Maxwell sono lineari: potremo immaginare le
soluzioni generali come combinazioni lineari di soluzioni più
semplici
Definiremo quindi:
modi TE (trasverso-elettrici) quelli per cui Ez=0
 modi TM (trasverso-magnetici) quelli per cui Hz=0
 modi TEM (trasverso-elettromagnetici) quelli per cui
simultaneamente Ez=Hz=0



Chiaramente, l’equazione d’onda scalare in Hz (+condizioni
al contorno) sarà sufficiente per determinare i campi dei
modi TE
Viceversa per i TM sarà sufficiente lavorare su Ez

Cosa succede con i TEM?


Abbiamo appena detto che nel caso particolare TEM
k
2

 2  0
Per cui in tale caso specifico l’equazione diventa
t E  0
2

A tutti gli effetti, una coppia di equazioni di Laplace. Le onde
TEM hanno quindi la particolarità di avere distribuzioni di
campo nei piani trasversali (sia la componente elettrica che
magnetica: analoga equazione di otterrebbe per H), del tutto
simili alle distribuzioni di campo elettrostatico e
magnetostatico nella stessa struttura, con la differenza
fondamentale che si propagano in z con costante k
Particolarizziamo le equazioni che avevamo ricavato al
caso TEM
j
j

E


j

H
 y
Hy 
Ex 
Ex  Ex /
x


j 

H

j

E

y
x
H x  E y /

1

H  uz E






Relazioni simili alle onde piane (che ne sono un caso
particolare)
Si propagano per ogni frequenza, visto che in assenza di
perdite
   jk Sempre immaginario
Le soluzioni dipendono chiaramente dalle condizioni al
contorno, ma possono essere non banali solo se queste
costituiscono un dominio non semplicemente connesso
Pensate all’elettrostatica: se non potete individuare due
punti a potenziale diverso, il gradiente del potenziale
(perciò il campo elettrico) è identicamente nullo

In generale, per n conduttori, otterremo n-1 soluzioni
indipendenti non banali: n-1 MODI TEM
+
+
Jz
Modo PARI


-
+
Jz
Modo DISPARI
Nell’esempio di sopra abbiamo due strisce metalliche ed
un piano (o scatola) di massa: 2 modi
Si tratta di un caso particolare, ovvero SIMMETRICO, nel
qual caso di definisce PARI il caso in cui le componenti
tangenziali del campo magnetico si annullano sul piano di
simmetria, e DISPARI quelle in cui sono le componenti
tangenziali del campo elettrico ad annullarsi

Trattiamo il caso TM: in tal caso dovremo risolvere l’eq.


t E z  k 2   2 E z  0
2


Definiamo in particolare

  k  kc 2
2
2
Dovremo imporre che le componenti tangenziali di E siano
nulle sulla guida metallica (se metallica ideale): questo
garantisce l’unicità della soluzione

Et

z
Tuttavia, basterà imporre che Ez sia
nulla sulla guida per assicurarsi che
tutte le componenti tangenti lo siano
Del resto possiamo ricavare una
relazione semplice per avere le
componenti tangenziali da E
Ex  
Ey 


1
 k
2
1
 k
2
2
 x E z  j  y H z 
  y E z  j  x H z 
2
Ovvero, vettorialmente

  k  kc

kc
2
Ey  

kc
2
 x Ez

kc
2
 y Ez
t Ez
Vediamo le proprietà della costante di propagazione:
ricaviamola dalla definizione di kc
2

Et  


2
2
   kc  k
2
2
2
    kc 2  k 2
Mentre k dipende dalla frequenza, kc dipende
fondamentalmente dalle condizioni al contorno
Per frequenze basse, il termine sotto radice è positivo e la
costante di propagazione REALE: ATTENUAZIONE

Ridefiniamo kc

Così che la pulsazione c costituisca la pulsazione a cui  =0
  a  kc

k c   c 
 f 
1   
 fc 
2
Posto su un grafico
a( f)
fc
f

Invece per >c
 fc 
  jb  jk 1   
 f 

2
Posto su un grafico

b ( f)
k( f )
k
fc
f
Notate che per
frequenze alte, la
costante di
propagazione si
avvicina a quella
della luce

La velocità di fase è, per definizione, il rapporto tra
pulsazione e costante di propagazione
vp   / b 


2

1   fc  
1   
   f  

1
2
Al “taglio” diviene infinita, e decresce per frequenze
maggiori
Quando la velocità di fase dipende dalla frequenza, il
modo si definisce “dispersivo”. In particolare la dipendenza
dalla frequenza decrescente si definisce “dispersione
normale”

La velocità di gruppo è, per definizione, il rapporto tra le
variazioni di pulsazione e costante di propagazione
v g  d / db 


1
2 2
1   f c  
1   
   f  
Essa rappresenta la velocità dell’inviluppo di un pacchetto
di onde
Notiamo che il rapporto tra componenti ortogonali di
campo elettrico e magnetico è
Ey
Ex



Hy
Hx
j
Ht 
1
Z 0TM
u z  Et

Quantità che definiamo
impedenza modale TM, così da
poter scrivere
fc
vp( f )
vg( f )
c
f