campionamento2

Il DEFF
Il DEFF (Design EFFect) è l’Effetto del Piano di
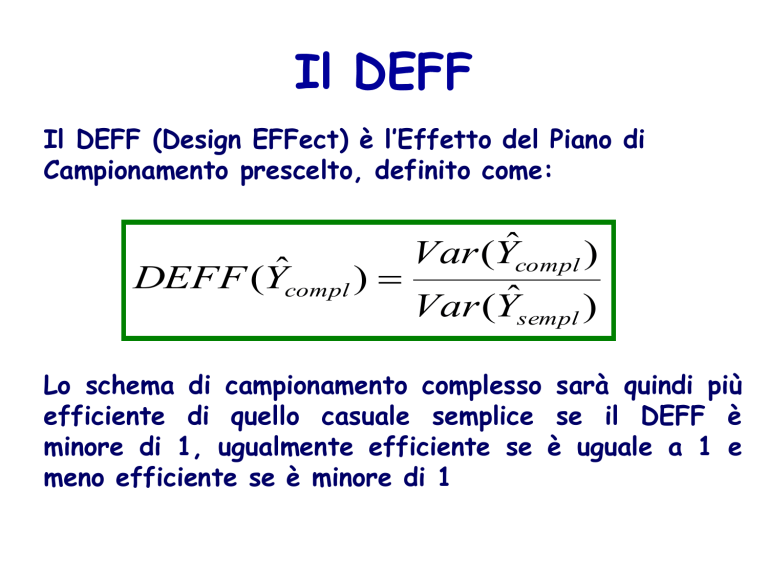
Campionamento prescelto, definito come:
ˆ
Var
(
Y
)
compl
DEFF (Yˆcompl ) 
Var (Yˆ
)
sempl
Lo schema di campionamento complesso sarà quindi più
efficiente di quello casuale semplice se il DEFF è
minore di 1, ugualmente efficiente se è uguale a 1 e
meno efficiente se è minore di 1
Campionamento casuale
<< STRATIFICATO>> (1)
«Stratificare significa ripartire la popolazione
sottopopolazioni dette strati »
PERCHE’ Stratificare ?
 Evidenziare
in
insiemi di unità particolari (unità
rare, gruppi estremali o devianti, come le grandi imprese)
 Separare
dagli altri, strati fisicamente isolati o
con caratteristiche speciali
 Individuare
particolari
unità da osservare con tecniche
Introdurre sulla selezione il massimo controllo, pur
mantenendo la casualità
Campionamento casuale
<< STRATIFICATO>> (2)
INDIVIDUARE SOTTOPOPOLAZIONI AL
MASSIMO OMOGENEE RISPETTO ALLA
VARIABILE (o alle variabili) DA RILEVARE
STIME
PIU’
EFFICIENTI
di
quelle
ottenibili con un campionamento casuale
semplice (di pari numerosità)
Campionamento casuale
<< STRATIFICATO>> (3)
Ogni strato Ph è una popolazione
Se la popolazione P è suddivisa in H strati
allora
H
h 1 Ph  P
Il campione Ch estratto dallo strato h è
idoneo a rappresentarlo
H
h 1 C h  C
Rappresenta l’intera popolazione P
Campionamento casuale << STRATIFICATO>> (4)
REGOLE per la stratificazione
Le
CARATTERISTICHE
per
la
stratificazione devono essere note prima
della selezione
Ogni
unità statistica deve appartenere
ad uno e ad un solo strato
STRATIFICATO
è un campione estratto
da una popolazione STRATIFICATO
Il campionamento stratificato proporzionale
Da ogni strato si seleziona un campione casuale
mantenendo la proporzione dello strato nella
popolazione (k = 1, …, K con K numero degli strati):
fk = nk / Nk = f = n/N
Campionamento casuale << STRATIFICATO>> (5)
Selezione di un campione
stratificato OTTIMALE
La
frazione di campionamento che permette di
raggiungere l’obiettivo è più elevata negli strati in
cui la variabilità è maggiore, rispetto a quelli in cui
i valori si addensano attorno ai valori medi
A
parità di varianza, si campionerà negli strati
in cui il costo unitario di rilevazione è più basso:
Whs h C h
nh  n H
h 1Whs h C h
dove sh è lo scarto quadratico medio della variabile scelta come
fattore di stratificazione all’interno dell’h-esimo strato
Campionamento casuale << STRATIFICATO>> (6)
Selezione con ALLOCAZIONE OTTIMA secondo
Neyman (1934) e Chuprov (1923)
Quando
non si hanno vincoli di costo, o quando il
costo è uguale in tutti gli strati, la numerosità
ottima per l’h-esimo strato è data da:
Whs h
nh  n H
h 1Whs h
N.B. può accadere che nh > Nh. Si campioneranno,
allora le Nh unità e si aumenterà la numerosità da
attribuire agli altri (H-1) strati, ignorando l’h-esimo
Campionamento casuale << STRATIFICATO>> (7)
STIMA con ALLOCAZIONE OTTIMA
Il
campione stratificato con allocazione ottima
delle unità non è autoponderante
Occorre,
quindi, introdurre un sistema di pesi wi
nel calcolo delle stime per tener conto delle
differenti probabilità di inclusione pi delle singole
unità (schema di campionamento con probabilità
variabili)
wi 
1
pi
Campionamento casuale << STRATIFICATO>> (8)
STIMA con ALLOCAZIONE OTTIMA della
MEDIA m della variabile X
Chiamiamo:
 mh
la media della variabile X, all’interno dell’h-esimo strato
della popolazione
 X la
media della variabile X, all’interno dell’h-esimo strato
del campione
 s2 h
la varianza della variabile X, all’interno dell’h-esimo
strato della popolazione
 s2h
la varianza della variabile X, all’interno dell’h-esimo
strato del campioni
Campionamento casuale << STRATIFICATO>> (9)
STIMA con ALLOCAZIONE OTTIMA della
MEDIA m della variabile X
La MEDIA m della variabile X è corretta stimata
dalla media aritmetica ponderata delle medie
stimate nei singoli strati:
x ott  h 1Wh x h  h 1 Nh x h N
H
x h  i 1 x hi nh
nh
H
Campionamento casuale << STRATIFICATO>> (5)
Selezione di un campione
stratificato OTTIMALE
La
frazione di campionamento che permette di
raggiungere l’obiettivo è più elevata negli strati in
cui la variabilità è maggiore, rispetto a quelli in cui
i valori si addensano attorno ai valori medi
A
parità di varianza, si campionerà negli strati
in cui il costo unitario di rilevazione è più basso:
Whs h C h
nh  n H
h 1Whs h C h
dove sh è lo scarto quadratico medio della variabile scelta come
fattore di stratificazione all’interno dell’h-esimo strato
Campionamento casuale
<< A STADI>> (1)
«Alla base di un campionamento a stadi c’è una
struttura gerarchica della popolazione » :
la popolazione finale delle unità è contenuta in un
insieme di unità di livello superiore, che possono a
loro volta appartenere ad un numero più ridotto di
insiemi di dimensione più ampia
Esempio:
Si campiona in un primo stadio fra i comuni italiani.
Successivamente al secondo stadio si campionano
le famiglie all’interno dei comuni estratti.
Si intervistano, quindi, tutti i componenti delle
famiglie estratte (grappolo)
Campionamento casuale
<< A STADI>> (2)
Si noti che :
•
•
•
la successione gerarchica dei campionamenti può
non coincidere con la struttura della popolazione
l’estrazione del campione si può effettuare con
criteri differenti ad ogni stadio:
o con probabilità costanti o variabili
o da liste stratificate o meno
la stratificazione si effettua di regola al primo stadio,
perché è più economico e si hanno più informazioni
fissata la numerosità campionaria si può decidere
come combinare i diversi stadi
AMPIA FLESSIBILITA’
Campionamento casuale
<< A STADI>> (3)
Le fasi di un campionamento a stadi sono :
1. individuare il numero degli stadi
2. individuare le caratteristiche per stratificare (di
solito le unità di primo stadio)
3. decidere quante unità estrarre ad ogni stadio
4. decidere come selezionare ad ogni stadio
Il DEFF di un campionamento a stadi è inversamente
legato al coefficiente di correlazione interclasse
Campionamento casuale << RUOTATO>>
«Quando con l’indagine si vogliono stimare le
caratteristiche della popolazione ad intervalli di
tempo esistono diverse soluzioni » :
1. si costruisce un campione permanente, il panel
Vantaggi: consente di studiare flussi e persistenze
Limiti: rischio di perdita di rappresentatività col tempo
2. si selezionano campioni indipendenti ogni volta
Vantaggi: garantisce la rappresentatività nel tempo
Limiti: consente confronti temporali solo per aggregati
3. si sostituiscono a rotazione alcune unità
Vantaggi: presenta il vantaggio della continuità (parziale)
Limiti: complessità dei processi di stima
LO SCHEMA DI ROTAZIONE
«Un campione di dimensione n costante nel tempo può
essere visto come composto da n’ unità incluse
nella prima rilevazione
seconda e così via »
+
n’’ unità incluse nella
P=n’/n
è la frazione di sovrapposizione tra due periodi successivi
Si definiscono g gruppi di rotazione che hanno
generalmente uguale dimensione n/g
Il DEFF di un campionamento ruotato è legato al
coefficiente di auto-correlazione e alla frazione di
sovrapposizione
Un semplice schema di ROTAZIONE
Consideriamo il caso più semplice con:
P=1/2
SCHEMA PER T RILEVAZIONI
GRUPPI DI
ROTAZIONE
1
2
…
T-1
T
OCCASIONI DELL’ INDAGINE
1
x
x
2
x
x
…
…
…
…
…
…
T-1
x
x
T
x
x