Angolo tra due rette e bisettrice
330
340
350
N
10
20
30
40
320
50
310
60
300
70
290
280
80
W
E
260
100
110
250
120
240
130
230
220
210
200 190
S
170
160
150
140
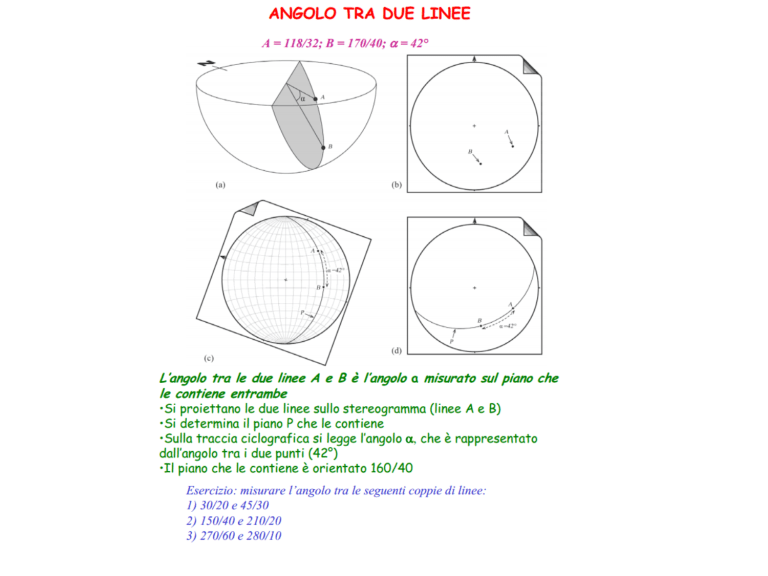
Due rette non parallele s’intersecano formando due angoli, per calcolare uno di essi si
ruotano i due punti fino a trovare la ciclografica che passa per essi, poi si misura l’angolo
compreso tra i due punti tenendo la ciclografica sul N-S. La misura che si ottiene può
essere <90° (angolo acuto) o >90° (angolo ottuso) oppure 90° (angolo retto). L’altro
angolo si ottiene come complementare (90°-angolo misurato).
La bisettrice di un angolo si ottiene dividendo l’angolo in due partendo da uno dei due
punti.
Angolo acuto tra due rette=84°
36°
bisettrice
48°
96°
Angolo diedro tra due piani
Angolo diedro tra due piani
330
340
350
N
10
20
30
40
320
50
310
60
300
70
290
280
80
W
E
260
100
110
250
120
240
130
230
220
210
200 190
S
170
160
150
140
Per calcolare l’angolo diedro tra due piani si proiettano i piani come ciclografiche, dalla
loro intersezione (linea) si misurano due angoli di 90° e si disegnano i due punti, poi si
traccia la ciclografica passante per questi due punti e si misura l’angolo compreso (acuto,
ottuso o retto). Per calcolare la bisettrice il procedimento è analogo a quello per le linee.
Angolo diedro tra due piani
Angolo diedro tra due piani=72°
108°
bisettrice
A Simple Theory (Anderson's) of Fault Mechanics:
Anderson's theory of faulting
explains a lot of what we see,
but certainly not all faulting.
For example, faults may
preferentially develop on preexisting fractures.
From study of brittle failure in the lab we know that shear planes develop at about +30 degrees
to Sigma 1. These are called conjugate shear fractures, are separated by about 60 degrees from
each other and provide an immediate clue to stress orientations.
The earths surface is a free surface ( a contact between the ground and air or water) and cannot
be subject to a shear stress. Therefore one of the principal stresses must be perpendicular to
the free surface. Only planes of stress ellipse (or state of stress) without shear stress are
principal planes, that is planes perpendicular to one of the maximum principal stresses.
When Sigma 1 is vertical normal faulting occurs with the intersection of the conjugate faults
along Sigma 2.
When Sigma 1 is horizontal and Sigma 3 is vertical thrust faulting occurs.
When Sigma 2 is vertical (and Sigma 1 and Sigma 3 are horizontal) strike slip faulting occurs.
s1
s3
s2
Pitch: l’angolo che una stria o fibra (su un piano di faglia) forma con la direzione del piano. L’angolo è misurato da
destra o sinistra (bisogna indicare l’orientazione) ed è minore o uguale a 90°. Se è minore di 45° allora prevale la
componente di trascorrenza (strike-slip) se invece è maggiore prevale la componente dip-slip (normale o inversa)
pitch
Esercizio2: faglia obliqua 220/65 con componente normale, pitch=40° NW
Disegnare la ciclografica con le strie e determinare il trend e plunge delle strie.
Pitch
Stria=295/36
Qual è l’altra componente cinematica? Trascorrenza destra o sinistra?
Esercizio3: faglia obliqua 065/30, una componente è di trascorrenza sinistra e il pitch è 20°
SE, calcolare il trend e plunge delle strie e determinare l’altra componente cinematica.
Per calcolare il trend e plunge di una stria si traccia prima la ciclografica che rappresenta il
piano, poi si conta lungo la ciclografica ruotata sul N-S l’angolo di pitch (ricordando il lato
dove si deve iniziare a contare indicato dal numero cardinale associato alla misura di pitch),
poi si segna il punto (che rappresenta la stria ovvero una linea) e si porta sull’E-W per
calcolare il trend e plunge.
Faglia e Pitch
Stria=136/10
Cinematica trascorrente
sinistra con componente
inversa
Calcolare s1, s2 e s3, slip vector e cinematica dominante
dati due piani di faglia:
F1= 024/74
F2=225/32
s2
s1
Si calcolano i punti posti a 90° dall’intersezione
delle faglie (s2) questi corrispondono agli slip
vector s1 e s2
s2
Poi si calcola la bisettrice dell’angolo compreso, se
questo è acuto la bisettrice corrisponde a s1, se
ottuso a s3.
s1
s2
s3
s1
s2
Poi si calcola s3 a 90° da s1 (nel caso in esame)
lungo la ciclografica.
s1
s2
s3
s1
Infine si definisce la cinematica dominante
(in questo caso normale perché lo stress più
vicino alla verticale, cioè il centro del
reticolo, è s1) e si tracciano le frecce
partendo dagli slip vector (verso l’esterno
per le faglie normali, verso l’interno per
quelle inverse e doppie frecce per le
trascorrenti).
Strutture S-C
Cinematica normale
Cinematica trascorrente
Cinematica inversa
In sezione
In pianta
Si proiettano i piani S e C e partendo dalla
loro intersezione si misura 90° lungo il
piano di taglio C e si segna lo slip vector.
La cinematica è indicata da una freccia.
C
S
90°