Recupero_2006

Prova di recupero corso di Fisica 4
8/05/2006 I parte
COGNOME………………...
NOME………….....………..
Esercizi numerici
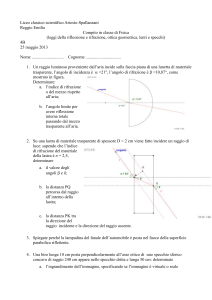
1) In figura un sottile raggio di luce incide con angolo  = 45° sulla faccia di un cilindro di materiale
trasparente con indice di rifrazione n. Il fascio rifratto viene riflesso totalmente sulla superficie laterale
del cilindro. Calcolare l’indice di rifrazione minimo n per cui sia verificata questa condizione.

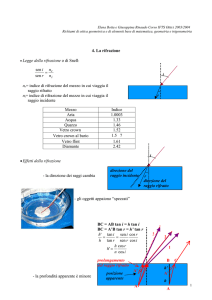
1) Un fascio di luce proveniente dall’aria incide su una lastra a facce piane e parallele con indice di
rifrazione n2 = 1.50. La radiazione è polarizzata linearmente nel piano di incidenza (vedi figura); il
raggio rifratto incide poi su una superficie che delimita un mezzo con indice di di rifrazione n3. In
entrambe le rifrazioni alle interfacce l’intensità riflessa è zero. Si calcoli n3.
1
2
n2
n3
3) Se lo specchio mobile di un interferometro di Michelson viene spostato di d = 0.233 mm si osserva
uno spostamento di 792 frange. Qual è la lunghezza d’onda della luce utilizzata? Se invece viene
inserita in uno dei due bracci una sottile lamina di materiale con indice di rifrazione n = 1.40 si osserva
lo spostamento di 7.0 frange. Qual è lo spessore t della pellicola?
Quesiti (MAX 30 parole)
A) Scrivere le componenti del campo elettrico di un’onda elettromagnetica piana polarizzata
linearmente lungo una direzione a 45° con l’asse y che si propaga lungo l’asse x con un’ampiezza
E0 in un mezzo con costante dielettrica .
B) Qual è l’espressione dell’intensità luminosa in funzione dell’ampiezza del campo elettrico e del
campo magnetico di un’onda monocromatica?
C) Quali grandezze sono legate dalle relazioni di Fresnel?
D) Definire la coerenza spaziale e temporale.
E) Descrivere almeno due effetti prodotti dalla dispersione.
Soluzioni
1)

1
sen  nsen1
dalla legge di Snell:
2
 sen1 
dalla trigonometria e dalla condizione di angolo limite:
 2  90  1
n 
1

cos 1
 sen 2  cos 1  sen l 
1
1  sin 1 
 2n 2  1 
 1
n 
2 
2
n


2
2

1
1
1
2n 2
 n 2  1.5  n  1.22
1
n
sen
2

n
2n
2)
si tratta evidentemente di rifrazioni all’angolo di Brewster:
prima interfaccia:
tg1  n2
seconda interfaccia:
sin  2 
 n2 cos1  sin 1  n2 sin 2
n3
n
cos  2  3 sin 1  n3 sin  2
n2
n2
dal primo e dall’ultimo membro:
3)
n3  1
2d  N1    588 nm
n  12t
 N 2  t 
N 2
 5.14 m
2n  1
Prova di recupero corso di Fisica 4
8/05/2006 II parte
COGNOME………………...
NOME………….....………..
Esercizi numerici
1) Una bolla d’aria sferica di raggio R = 1 cm è immersa in un liquido con indice di rifrazione n = 3. Un
insetto si trova nel punto A all’interno della bolla a distanza R/2 dal bordo. Calcolare la posizione e le
caratteristiche dell’immagine dell’insetto e effettuare il tracciamento dei raggi.
n
nB = 1
C
A
2) Si vuole costruire un telescopio astronomico a rifrazione utilizzando una prima lente con lunghezza
focale f1 = 100 cm. La seconda lente utilizzata sia pianoconvessa con raggio di curvatura R e fatta di
vetro con indice di rifrazione n = 1.58. Determinare il valore di R per ottenere un ingrandimento
angolare del telescopio M = 50.
3) Una lente convergente di lunghezza focale f1 = 10 cm è posta a una distanza d = 40 cm da una lente
divergente con f2 = 20 cm. Un oggetto è situato a 50 cm dalla prima lente. Calcolare la posizione e le
caratteristiche dell’immagine e tracciare il diagramma dei raggi.
50 cm
2
1
40 cm
Quesiti (MAX 30 parole)
A) Scrivere la forma Newtoniana dell’equazione delle lenti specificando il significato dei termini
B) Spiegare il fenomeno dell’aberrazione cromatica e le sue cause
C) Scrivere l’espressione per la posizione dei minimi di intensità in un processo di diffrazione da
fenditura alla Fraunhofer.
D) Una lastra di vetro spessa 3 cm lascia passare lo 0.5 % della luce che la colpisce. Trascurando la
riflessione, quanto vale il coefficiente di assorbimento del vetro e l’assorbanza della lastra?
E) Che colore si vedrà guardando verso il mezzo
diffondente rispettivamente lungo x, y, z?
x
E (t)
mezzo diffondente
luce bianca
polarizzata x
z
k
y
Soluzioni
1)
dalla teoria del diottro concavo aria/liquido sarà:
n1
n
n n
 2  2 1
s
s'
R
con R < 0 si ottiene:
m  
f' 
nB s '
1

ns
2

nRs
s'  
 s(n  nB )  Rn B

s' 



3
R   0.75 cm
4
immagine virtuale, rimpicciolita e dritta
n2 R
3

R  1.5 cm
n2  n1
2
n
nB = 1
F
C
A
2)
Dall’espressione per l’ingrandimento angolare ricaviamo:
M 
f1
f2
 f2 
f1
 2 cm
M
quindi, dall’equazione del costruttore di lenti:
 1
1
1 

 ( n12  1)

R

f
R
2 
 1
avendo posto:
3)
prima lente:
m1  
R2  
1
1
1


s1
s1 '
f
 s1 ' 
f  s1
 12.5 cm
s1  f
s1 '
  0.25
s1
seconda lente:
s2 ' 
 R1  (n21  1) f 2  1.16 cm
1
1
1


s2
s2 '
f
f  s2
  11.58 cm
s2  f
con s2  d  s1 '  27.5 cm
m  
s1 '  s2 ' 
      0.105
s1  s2 
F1 F2
immagine virtuale, rovesciata, rimpicciolita