file

I triangoli e i criteri di congruenza
Definizione
I triangoli
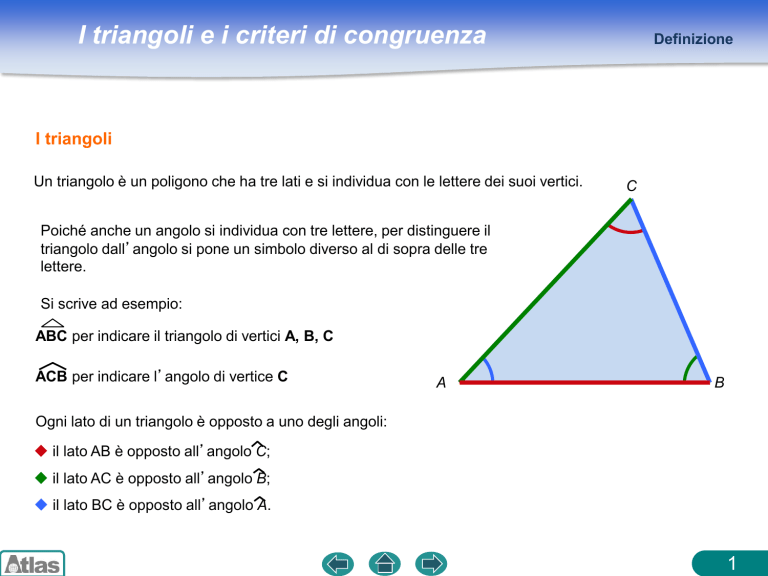
Un triangolo è un poligono che ha tre lati e si individua con le lettere dei suoi vertici.
C
Poiché anche un angolo si individua con tre lettere, per distinguere il
triangolo dall’angolo si pone un simbolo diverso al di sopra delle tre
lettere.
Si scrive ad esempio:
ABC per indicare il triangolo di vertici A, B, C
ACB per indicare l’angolo di vertice C
A
B
Ogni lato di un triangolo è opposto a uno degli angoli:
 il lato AB è opposto all’angolo C;
 il lato AC è opposto all’angolo B;
 il lato BC è opposto all’angolo A.
1
I triangoli e i criteri di congruenza
CLASSIFICAZIONE
Classificazione
DEI TRIANGOLI IN BASE AI LATI
È possibile fare una prima classificazione dei triangoli in base ai lati:
Scaleno: un triangolo che ha
tutti i lati disuguali.
Isoscele: un triangolo che ha
due lati congruenti. I due lati
congruenti si dicono obliqui e il
terzo lato si chiama base.
Equilatero: un triangolo che
ha tutti i lati congruenti.
2
I triangoli e i criteri di congruenza
Bisettrici e mediane
Si dice inoltre:
 bisettrice relativa ad un angolo interno del triangolo
sia la semiretta bisettrice dell’angolo, sia il segmento di
bisettrice che ha un estremo nel vertice dell’angolo e
l’altro sul lato opposto
 mediana di un triangolo il segmento che unisce un
vertice con il punto medio del lato opposto
3
I triangoli e i criteri di congruenza
I criteri di congruenza
Primo criterio di congruenza. Due triangoli sono congruenti se hanno ordinatamente congruenti due lati
e l’angolo fra essi compreso.
C’
C
A
B
ACB
≅
≅
≅
A’C’B’
ABC
≅
A’B’C’
CA
CB
C’A’
A’
B’
C’B’
4
I triangoli e i criteri di congruenza
I criteri di congruenza
Secondo criterio di congruenza. Due triangoli sono congruenti se hanno un lato e gli angoli ad esso
adiacenti ordinatamente congruenti.
A’
A
ABC
≅ B’C’
≅ A’B’C’
ACB
≅
A’C’B’
ABC
≅
A’B’C’
BC
B
C
B’
C’
5
I triangoli e i criteri di congruenza
I criteri di congruenza
Terzo criterio di congruenza. Due triangoli sono congruenti se hanno i tre lati ordinatamente congruenti.
A’
A
B
C
AB
≅
A’B’
AC
≅
A’C’
BC
≅
B’C’
ABC
≅
A’B’C’
B’
C’
6
I triangoli e i criteri di congruenza Le proprietà del triangolo isoscele
Teorema. In un triangolo isoscele gli angoli adiacenti alla base sono congruenti.
Viceversa, si può dimostrare anche che
Teorema. Se un triangolo ha due angoli congruenti, esso è isoscele.
B
A
AB
≅
BC
BAC
≅
BCA
C
I due teoremi si possono esprimere con un solo enunciato dicendo:
condizione necessaria e sufficiente affinché un triangolo sia isoscele è che abbia due angoli congruenti.
7
I triangoli e i criteri di congruenza
Le proprietà dei triangoli
Il teorema dell’angolo esterno
Teorema. In ogni triangolo ogni angolo esterno è maggiore di ciascuno degli angoli interni ad esso non
adiacenti.
A
δ>α
α
δ>β
β
B
δ
C
S
Da ciò consegue che:
 un triangolo non può avere più di un angolo retto o di un angolo ottuso;
 gli angoli alla base di un triangolo isoscele sono acuti.
8
I triangoli e i criteri di congruenza
CLASSIFICAZIONE
Classificazione
DEI TRIANGOLI IN BASE AGLI ANGOLI
Acutangolo
Un triangolo che ha tutti gli
angoli acuti.
Ottusangolo
Un triangolo che ha un
angolo ottuso.
Rettangolo
Un triangolo che ha un
angolo retto.
9
I triangoli e i criteri di congruenza
Il quarto criterio di congruenza
Il quarto criterio di congruenza
Il seguente criterio è una conseguenza diretta del teorema dell’angolo esterno.
Quarto criterio di congruenza. Due triangoli sono congruenti se hanno due angoli e il lato opposto a uno
di essi ordinatamente congruenti.
A’
A
ABC
≅
A’B’C’
≅ B’A’C’
BC ≅ B’C’
BAC
B
B’
C
ABC
≅
C’
A’B’C’
10
I triangoli e i criteri di congruenza
Relazioni fra lati e angoli
C
In ogni triangolo, se due lati sono
disuguali, al lato maggiore è opposto
l’angolo maggiore.
AB > AC
ACB > CBA
Viceversa:
In ogni triangolo, se due angoli sono
disuguali, all ’ angolo maggiore è
opposto il lato maggiore.
B
A
C
’
C
Se due triangoli hanno due lati
ordinatamente congruenti e gli angoli
compresi sono disuguali, allora i lati
opposti a questi angoli sono
anch ’ essi disuguali nello stesso
verso.
A
B
A
B
’
’
AC ≅ A’C’ CB ≅ C’B’ C > C’
AB > A’B’
11
I triangoli e i criteri di congruenza
Disuguaglianze triangolari
Dalle proprietà elencate precedentemente si può dedurre che:
 in ogni triangolo rettangolo l’ipotenusa è maggiore di ciascuno dei cateti;
 in ogni triangolo ottusangolo, il lato opposto all’angolo ottuso è maggiore di ciascuno degli altri due lati.
Vale poi il seguente importante teorema:
Teorema. In ogni triangolo ciascun lato è minore della somma degli altri due ed è maggiore della loro
differenza.
C
AC – CB < AB < AC + CB
AC – AB < CB < AC + AB
AB – CB < AC < AB + CB
A
B
12