FisDispStSol7

Transistor a giunzione bipolare
Inventato nel 1948-49, con ruoli diversi, da Bardeen,
Brittain, Shockley. Valse loro nel 1956 il premio Nobel
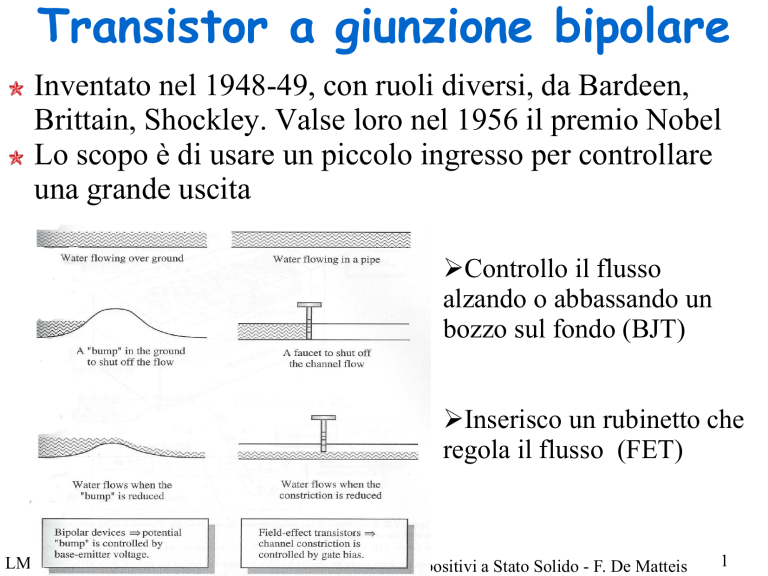
Lo scopo è di usare un piccolo ingresso per controllare
una grande uscita
Controllo il flusso
alzando o abbassando un
bozzo sul fondo (BJT)
Inserisco un rubinetto che
regola il flusso (FET)
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
1
Transistor bipolare: descrizione concettuale
Essenzialmente consiste in un
doppio diodo n+pn (o
viceversa)
La regione ad alto drogaggio
(n+) è chiamato emettitore, la
regione p base e la regione n
collettore
Nde>>Nab assicura che un piccolo cambiamento della
corrente di base provoca un grande aumento della
corrente di collettore
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 2
Transistor bipolare: descrizione concettuale
C'è poca ricombinazione Fattore B≤1
EBJ la giunzione emettitore-base è
polarizzata direttamente mentre la BCJ la
giunzione base collettore è polarizzata
inversamente
Il BJT è detto essere polarizzato in modo
diretto attivo.
Quando gli elettroni sono iniettati
dall'emettitore la gran parte di essi
attraversa la base senza problema.
A causa del forte campo base -collettore
gli elettroni sono spinti via e formano la
corrente di collettore (I=ev=emF)
Inoltre la superficie della BCJ è molto più
grande della EBJ
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 3
Azione del Transistor: descrizione concettuale
Se il diodo è n+-p, la corrente di polarizzazione diretta è fatta essenzialmente
dall'iniezione di elettroni nella zona p Questa corrente diretta può essere
alterata da una piccola variazione del potenziale di polarizzazione diretta
 eVb i k BT 
I V  = I 0  e
1


I C = BI En
Fattore di trasporto di base
Portatori minoritari sulla
giunzione pn
Rapporto di trasferimento di corrente
IC
BI En
=
= Bγe = α
I E I En + I Ep
I En
γe =
I En + I Ep
Efficienza di emettitore
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 4
Transistor bipolare: circuito tipico in
polarizzazione diretta attiva
Un piccolo cambiamento nella corrente di base causa un
grande cambiamento nella corrente di collettore.
L'amplificazione è data dal rapporto tra corrente di base e
quella di collettore.
La corrente di base è costituita da corrente di buche iniettata
nell'emettitore IEp e dalla corrente di buche che ricombinano
nella zona della base (1-B)IEn. Si è assunto che la giunzione
pn base-collettore è fortemente polarizzata inversamente e
quindi non dà corrente (di buche).
La corrente di base che stiamo prendendo in considerazione è
quella che entra (esce) dalla base (non quella che scorre nella
base).
I B = I Ep + 1  B I En
Ic
BI En
β= =
=
I B I Ep + 1  B I En
BI En / I E 
Bγe
=
= hFE
1  BI En / I E  1  Bγe
LM Sci&Tecn dei Materiali A.A.2015/16
Fattore di amplificazione di
corrente Base-Collettore
α
β = hFE =
1 α
Fisica dei Dispositivi a Stato Solido - F. De Matteis
5
Polarizzazione del BJT
Modo di operazione
EBJ bias
CBJ bias
Saturazione
Diretto (VEB<0)
Diretto (VCB<0)
Attivo diretto
Diretto (VEB<0)
Inverso (VCB>0)
Cut-off
Inverso (VEB>0)
Inverso (VCB>0)
Attivo inverso
Inverso (VEB>0)
Diretto (VCB<0)
Dispositivi a
microonde
VEB=VB-VE
I diversi modi di operazione, singolarmente
o più di uno insieme, vengono sfruttati nel
funzionamento di diversi dispositivi
Applicazioni di accensione - spegnimento
Per tutto questo è importante capire le correnti bipolari che si generano
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
6
Flussi di corrente
Esaminiamo le varie correnti alla luce della teoria sulle
giunzioni pn viste precedentemente. (Modo Attivo diretto)
Wb = Wbn (dimensione dello strato neutro)
 eVBE k BT 
δpe xe = 0 = peo  e
1


 eVBE k BT 
δnb xb = 0 = nbo  e
1


Polarizzato diretto
Vij = Vi -Vj > 0
  eVCB k BT 
δnb xb = Wbn  = nbo  e
 1

 Polarizzato inverso
 eVCB


k BT

δpc xc = 0 = pco  e
 1


Le regioni di emettitore e collettore sono > Lp → andamento exp
La regione di base < Ln → andamento quasi lineare (su entrambe le giunzioni)
Dia 4.18
W  x 
x 
δn 0 sinh  bn b   δn Wbn sinh  b 
Ln 
Ln 


δn  xb  =
W 
sinh  bn 
 Ln 
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
7
Flussi di corrente
 eVBE

δpe xe = 0 = peo  e k BT 1


 eVBE k BT 
δnb xb = 0 = nbo  e
1


  eVCB k BT 
δnb xb = Wbn  = nbo  e
 1
 eV

CB


k BT
δpc xc = 0 = pco  e
 1


W  x 
x 
δn 0 sinh  bn b   δn Wbn sinh  b 
Ln 
Ln 


δn  xb  =
 Wbn 

sinh 
 Ln 

  eVCB  
 eVBE 

 k T

 k T





nbo
W

x
x
 sinh  bn b  e B  1 + sinh  b  e B

=

1

 L

L 
sinh Wbn / Lb  


b


 b 


 



 xe
Wep  L p
Wbn ≈ Lb
lp
δp e  xe  = δp e 0 e
δp c  xc  = δp c 0 e
 xc
lp
Wcp  L p
 dnb xb = 0
dpxe = 0 


I E = I Ep + I En = I + I = eA Db
 De
dxb
dxe


 Db nbo

 eVCB k BT 
De peo  eVBE k BT 
Db nbo
e
e
I E = eA
coth Wbn / Lb  
 1 + eA
 1
Le 


 Lb
 Lbsinh Wbn / Lb  
BE
p
EB
n
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
8
Flussi di corrente
 eVBE

δpe xe = 0 = peo  e k BT 1


 eVBE k BT 
δnb xb = 0 = nbo  e
1


  eVCB k BT 
δnb xb = Wbn  = nbo  e
 1
 eV

CB


k BT
δpc xc = 0 = pco  e
 1


 dnb xb = Wbn 
dpxc = 0 

 I C = I nBC + I pBC = eA Db
 Dp
dx
dx
b
c


 Db nbo

 eVBE
De peo  eVCB k BT 
Db nbo
e
 e
 I C = eA
coth Wbn / Lb +
 1  eA
 1
k BT 

Lc 

 Lb
 Lbsinh Wbn / Lb  
I B = I E  I c 
Wbn  Lb
Approx al primo
ordine non triviale
sinh α   α
coth α   1

Trascurando la corrente del diodo in polarizzazione
inversa Base-Collettore
 Db nbo
De peo  eVBE k BT 
e
I E = eA
+
 1
Wbn
Le 


D n 
I C = eA b bo  eeVBE
 Wbn 

k BT

1
 Db nboWbn De peo  eVBE k BT 
e
I B = eA
+
 1
2
Le 

 2Lb
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
9
Relazioni generali corrente-voltaggio
 eVBC k BT 
 eVBE k BT 
I E =  I ES e
 1   R I CS e
 1




 eVBC k BT 
 eVBE k BT 
I C =  F I ES e
 1  I CS e
 1




Guadagno di
corrente in base
comune (diretto
attivo)
I B = I E  Ic
VBC  0
 Db nbo
De peo 

I ES = eA
cothWbn / Lb +
Le 
 Lb
 Db nbo
Dc pco 


I CS = eA
cothWbn / Lb +
Lc 
 Lb
LM Sci&Tecn dei Materiali A.A.2015/16
VBE  0
 F I ES
Pol Dirette per
entrambe np e pn


Db nbo

  R I CS = eA
 Lbsinh Wbn / Lb  
Fisica dei Dispositivi a Stato Solido - F. De Matteis 10
Effetto Early o modulazione
dell’ampiezza di base
IB
b
IC
1
IC 
Wbn
In un transistor ideale in configurazione di emettitore comune ci si aspetta che ad una data
corrente di base IC sia indipendente daVEC per VEC> 0. Sarebbe così se potessimo assumere
che l’ampiezza della base neutra (W) è constante. Ma poiché l’ampiezza della regione di
carica spaziale che si estende nella regione della base varia con la tensione base-collettore,
l’ampiezza di base è funzione della tensione base-collettore. La corrente di collettore
dipende da VEC. All’aumentare della tensione inversa base-collettore,l’ampiezza di base si
ridurrà. Ciò causa un aumento del gradiente di concentratione dei portatori minoritari e
quindi un aumento della corrente di diffusione. L’amplificazione b aumenta ma questo non è
auspicabile per il dispositivo.
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 11
Avalanche breakdown
La tensione base-collettore che il transistor può sostenere è limitata da fenomeni di rottura a valanga.
Limite alla potenza che può essere ottenuta dal transistor. La rottura dovuta a ionizzazione di impatto
si rispecchia nelle caratteristiche I-V.
In configurazione di base-comune la rottura avviene a ben definite condizioni (tensione VCB limite)
In configurazione emettitore-comune la rottura avviene a tensioni che sono modulate dal valore del
parametro di ingresso.
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 12
Configurazioni operative del BJT
Profilo delle bande e
distribuzione dei
portatori di
minoranza per
operazioni in
saturazione, attiva
diretta e cut-off
In saturazione sia EBJ
che CBJ sono
polarizzate dirette e
una grande densità di
portatori di minoranza
sono iniettati nella
regione della base
(importante per lo
switching)
In modo di diretto attivo EBJ è polarizzata diretta e CBJ è polarizzata
inversa. E' usato per amplificazione IC >> IB
LM Sci&Tecn dei Materiali A.A.2015/16
In modo di cut-off sia
EBJ che CBJ sono
polarizzate inverse e
non c'è densità di
portatori di minoranza
nella regione della base
Fisica dei Dispositivi a Stato Solido - F. De Matteis
13
Parametri di funzionamento statici
I transistor bipolari possono essere polarizzati in tre diverse configurazioni ognuna con i suoi vantaggi.
Nella configurazione di base comune il modo di cut-off avviene quando la corrente di emettitore è nulla. Per correnti
IE non nulle il BCJ deve essere polarizzato diretto VBC<0 (~0,7V) per bilanciare le correnti iniettate dall'emettitore.
Nel modo di emettitore comune si ha cut-off per correnti di base quasi nulle. Il EBJ non è più polarizzata diretta. La
regione di saturazione occorre quando VCE = VBE ed entrambe le giunzioni sono polarizzate direttamente.
In amplificazione di piccoli segnali il dispositivo opera in modo attivo con alta corrente o guadagno di potenza.
In modo interruttore il dispositivo passa da cut-off (non conduttore) a saturazione (conduttore)
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
14
Parametri del BJT
Modo attivo diretto
eVBE >> kBT
eADe peo
I Ep = 
Le
eVCB>> kBT
I En  
Wb<<Lb
e
eVBE
k BT
eADb nbo
 Wbn 

Lb tanh 
 Lb 
e
eVBE
k BT
Come scegliamo i parametri costruttivi del BJT
Efficienza di iniezione di emettitore
I En
1
γe =
=
I En + I Ep 1+  peo De Lb / nbo Db Le tanh Wbn / Lb 
~Wbn/Lb
peo DeWbn
1
γe 
1
1 +  peo DeWbn / nbo Db Le 
nbo Db Le
Per disegnare un BJT con ge prossimo a 1 dobbiamo scegliere Wbn<<Le e peo <<nbo
(Wbn non può essere troppo piccola perché sorgerebbero altri problemi accessori)
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
15
Parametri del BJT
IC
Wbn Lb
1
B=

I En coshWbn / Lb 
Come scegliamo i parametri
costruttivi del BJT
Fattore di trasporto di base B
Wbn2
B  1 2
2L b
E' il rapporto tra la corrente che raggiunge il
collettore alla corrente base-collettore.
Essendo la giunzione base-collettore fortemente
polarizzata inversa tutta la corrente che giunge
sulla giunzione è risucchiata nel collettore
Come scegliamo i parametri
costruttivi del BJT
Guadagno di corrente
gc~1
( Bassa ricombinazione)
Come scegliamo i parametri
costruttivi del BJT
Efficienza di collettore gc
IC
BI En
α= =
= γe B
I E I En + I Ep
 peo DeWbn   Wbn2 
= 1 
 1  2 
nbo Db Le   2L b 

≤1
non può esserci un vero e proprio guadagno in senso stretto
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
16
Risposta a segnali AC
Piccolo segnale  l’ampiezza del
segnale in frequenza (AC) è molto
minore del segnale in continua (DC)
VEC  RL I C  VCC
x  RL y  VCC
La curva di carico ha pendenza –RL-1
e intercetta VCC
Bassa frequenza
I B
g

VBE
gEBEB
= IB/VBE
conduttanza di
ingresso
Alta frequenza
Circuito equivalente
LM Sci&Tecn dei Materiali A.A.2015/16
I C
g

gmm
=bgEBVBE
transconduttanza
IC
α
β =
= hFE
IB
1 α
Guadagno di corrente BaseCollettore
Ad alta frequenza occorre
considerare i contributi
capacitivi
CEB capacità svuotamento e Cd capacità di
diffusione (giunzione EB polar. diretta)
CCB capacità di svuotamento (giunzione CB polar.
inversa)
gEC conduttanza di modulazione di ampiezza di base
(piccola conduttanza  grande resistenza)
Fisica dei Dispositivi a Stato Solido - F. De Matteis 17
Risposta a segnali AC
gm e gEC dipendono da b e quindi da .
Il guadagno è costante solo a bassa frequenza

b0
α
β=

1  α 1 j f
fb
IC
α0
=
IE 1 j f
f
fb=f10
cut-off
Frequenza di cut-off di base
(/emettitore) comune f (/fb )
frequenza per cui /b si riduce a
1 2 del Max
β ( fT ) 
Frequenza a cui |b=1
b0
2
T
2
1
f
1
fb
fT  f b b02  1  b0 f b   0 f
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis 18
Tempo di risposta
La frequenza fT è legata al tempo di risposta del dispositivo ovvero al tempo necessario per un
portatore di transitare dall’emettitore al collettore. Questo include diversi contributi:
W dx
W qAn( x )
tE ritardo dell’emettitore, tB tempo di
t 

dx
transito della base, tC tempo di transito B
0 v( x)
0
IC
del collettore.
 qV / kT
 qV / kT
W qAn( x )We
W (W  x )e
Il più importante è il tempo di transito 
dx 
dx
0
0
qADn n p 0
Dn
della base tB
La distanza che percorrono i portatori
W2
minoritari nella base in un intervallo

2 Dn
di tempo è dx = v(x) dt, dove v(x) è la
velocità effettiva dei portatori minoritari nella base.
Transistor per alte frequenze sono disegnati con uno spessore ridotto della base. Poiché la
costante di diffusione elettronica è circa 3 volte superiore di quella delle buche, n-p-n sono
preferiti.
Un altro modo per ridurre il tempo di transito è di usare una base con drogaggio graduale
(maggiore in prossimità dell’emettitore e minore verso il collettore) Il campo indotto aiuta il
moto dei portatori riducendo il tempo di transito.


LM Sci&Tecn dei Materiali A.A.2015/16


Fisica dei Dispositivi a Stato Solido - F. De Matteis 19
Analisi dell’andamento di carica
Comportamento del dispositivo in termini di cariche nelle diverse regioni e costanti di
tempo legate al flusso di carica. In condizioni stazionarie la carica iniettata è costante ma
abbiamo comunque una corrente IC (IB)
Modo diretto attivo
Carica iniettata nella base (Area del
triangolo dei portatori minoritari iniettata)
eAWbn nbo  eVBE k BT 
 e
QF =
1 t F I C
2


Wbn2
Tempo di transito diretto
tF 
2 D p verso il collettore
Inoltre c’è una carica di giunzione che
dipende dalla tensione di polarizzazione
della giunzione
QV (V )   dQ j   C j V dV
C j V  
V
V
0
0
C j0
1  V
Vbi 
13
Per la base ci sono due contributi alla corrente
uno diffusivo (stazionario con tBF) ed uno di
accumulazione di carica dinamico
QF t  dQF t 
iB (t ) 

t BF
dt
IB
iC 
QF

dQVC
dt
iB 
QF

dQF dQVC dQVE


dt
dt
dt
tF
t BF
iE  iC  iB
Giunzione linear graded
(se fosse abrupt sarebbe ½)
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
20
Analisi dell’andamento di carica
Comportamento del dispositivo in termini di cariche nelle diverse regioni e costanti di
tempo legate al flusso di carica.
Modo inverso attivo
eAWbn nbo  eVBC k BT 
 e
QR =
1 t R I E
2


Tempo di transito inverso
verso l’emettitore
dQVE
iE  

tR
dt
QR
iB 
QR
t BR
dQR dQVC dQVE



dt
dt
dt
iC  iE  iB
Modo in saturazione
 1
1  dQR
 
iC 
 QR  
tF
 t R t BR  dt
QF QR d QF  QR 
iB 


t BF t BR
dt
QF
Combinazione dei due modi attivi. La
capacità di giunzione è trascurabile
perché la tensione di giunzione non
cambia molto una volta raggiunta la
condizione di saturazione
LM Sci&Tecn dei Materiali A.A.2015/16
iE  iC  iB
Fisica dei Dispositivi a Stato Solido - F. De Matteis
21
Transistor bipolare come inverter
Base della tecnologia digitale: circuiti logici
La risposta non è istantanea
t4
Accensione:
Da regione di cut-off a regione attiva td=t1-t0
EBJ e BCJ polarizzate inverse → regione attiva EBJ diretta.
Carica della regione di Base
t4
Spegnimento:
Da regione di saturazione a instaurarsi di
regione attiva ts=t4-t2
Si neutralizza la saturazione
Da regione attiva a saturazione tf=t2-t1
Regione attiva inversa a cut-off tr=t5-t4
22 22
Raggiunge
la saturazione
Raggiunge
regione
cut-off
LM
LMSci&Tecn
Fisica
A.A.2013/14
dei Materiali A.A.2015/16
Fisica dei Dispositivi
Fisica dei
a Stato
Dispositivi
Solido
-aF.Stato
De la
Matteis
Solido
- F.diDe
Matteis
Transistor bipolare come inverter
Da cut-off a regione attiva td=t1-t0
t=t0 VBE=0 VBC= - VCC =-5 V
TTL
i B ( t 0 )=
v i (t 0 )− V BE ( t 0 )
= 1 mA
RB
t=t1 VBE=0,7V VBC=VBE - VCC =-4,3V
 i t dt=
t1
t0
B
iB t1  t0   DQE  DQC
DQVE  C ej DVBE
vi  VBE ON 
= 0,86mA
RB
<iB>=0,93 mA
iB t1  =
DQ=0,527 pC
td=0,57 ns
Da regione attiva a inizio saturazione tf=t2-t1
t=t2 VBE=0,8 VBC=0,8 – 0,1=0,7 V
i B ( t 2)=
v i − V BE ( sat)
= 0,84 mA
RB
tf=1,97 ns
t(ON)=2,54 ns
LM Sci&Tecn dei Materiali A.A.2015/16
Fisica dei Dispositivi a Stato Solido - F. De Matteis
23
Transistor bipolare come inverter
Da saturazione a regione attiva ts=t4-t3
Il transistor possiede una grossa saturazione di carica
sulla base da estrarre per arrivare a BCJ polarizzata
inversa
ts=14,16 ns
Da regione attiva a cut-off tr=t5-t4
0  0,8
iB t4  =
= 0,16 mA
3
5x10
0  0,7
iB t5  =
= 0,14 mA
3
5x10
iB t6  = 0 mA
<iB>=0,07 mA
C'è ancora carica di svuotamento che
va recuperata (tD)
iB t6  t5  =DQV  0,527 pC
LM Sci&Tecn dei Materiali A.A.2015/16
tr=15,6 ns
t6-t5=7,5 ns
t(OFF)=37,26 ns
Fisica dei Dispositivi a Stato Solido - F. De Matteis
24