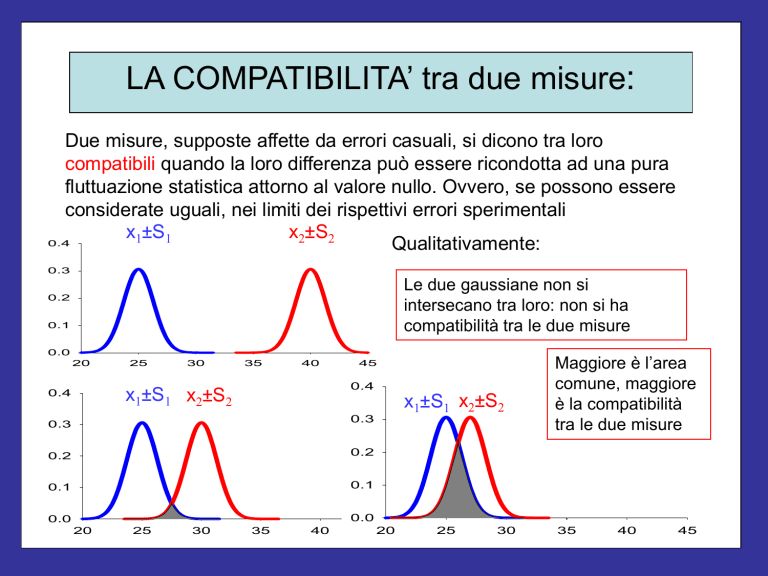
LA COMPATIBILITA’ tra due misure:
Due misure, supposte affette da errori casuali, si dicono tra loro
compatibili quando la loro differenza può essere ricondotta ad una pura
fluttuazione statistica attorno al valore nullo. Ovvero, se possono essere
considerate uguali, nei limiti dei rispettivi errori sperimentali
x1±S1
x2±S2
0.4
Qualitativamente:
0.3
Le due gaussiane non si
intersecano tra loro: non si ha
compatibilità tra le due misure
0.2
0.1
0.0
20
25
30
35
40
0.4
x1±S1 x2±S2
0.4
45
x1±S1 x2±S2
0.3
0.3
0.2
0.2
0.1
0.1
0.0
20
25
30
35
40
0.0
20
45
25
30
Maggiore è l’area
comune, maggiore
è la compatibilità
tra le due misure
35
40
45
LA COMPATIBILITA’ tra due misure:
Il grado di intersezione tra le curve non dipende solo dalla distanza
(differenza) tra i due valori medi, ma anche dalla larghezza delle gaussiane
x1±S1
0.4
x2±S2
Le due gaussiane non si
intersecano tra loro: non si ha
compatibilità tra le due misure
0.3
0.2
0.1
0.0
20
0.4
25
30
35
40
45
x1±S1
0.3
A parità di distanza tra i valori medi x1
e x2, la sovrapposizione tra le curve
cresce al crescere della loro
larghezza
0.2
x2±S2
0.1
0.0
20
30
40
50
60
LA COMPATIBILITA’ tra due misure:
E’ possibile quantificare la compatibilità tra due misure tramite il calcolo
dell’intervallo di confidenza (confidence level – CL) che indica la probabilità
che la differenza tra i due valori misurati sia una fluttuazione statistica
intorno al valore nullo.
Operativamente dati i due valori x1±S1 x2±S2 si calcola:
1) La differenza tra i due valori:
x1 x2
2) L’errore su questa differenza (propagazione
degli errori per somme e differenze):
3) Se ne fa il rapporto:
t
x1 x2
S12 S 22
Sdiff S12 S22
Minore è il valore di t, maggiore
sarà la compatibilità
4) Si ricava dalla tabella della gaussuana la probabilità associata P(t):
5) Se ne fa il complementare: CL 100 P (t )
Maggiore è il valore di CL,
maggiore sarà la compatibilità
In genere due misure si considerano compatibili se CL>5%, non compatibili se CL <0.3%
LA COMPATIBILITA’ tra due misure:
Determinare il livello di confidenza tra queste coppie di valori
Esempio:
x1±S1
x2±S2
25 ±1.3
40 ±1.3
25 ±1.3
30 ±1.3
t
40 25
1.32 1.32
30 25
1.3 1.3
2
25 ±1.3
28 ±1.3
2
28 25
1.3 1.3
2
25 ±1.3
40 ±1.3
1.3 7
0.4
0.3
0.2
0.1
0.0
25
30
2
40 25
2
20
35
40
45
2
15
8.1
1.84
5
2.72
1.84
P(t)
CL
>>99.999%
<<0.001%
99.35%
0.65%
3
1.63
1.84
89.96%
10.04%
15
2.11
7.12
96.51%
3.49%
LA COMPATIBILITA’ tra due misure:
Esempio:
Determinare il livello di confidenza tra queste coppie di valori
x1±S1
x2±S2
25 ±1.3
40 ±1.3
25 ±1.3
30 ±1.3
t
40 25
1.32 1.32
30 25
1.3 1.3
2
25 ±1.3
28 ±1.3
2
28 25
1.3 1.3
2
25 ±1.3
40 ±1.3
2
40 25
1.3 7
2
2
15
8.1
1.84
P(t)
CL
>>99.999%
<<0.001%
99.35%
0.65%
5
2.72
1.84
3
1.63
1.84
89.96%
10.04%
15
2.11
7.12
96.51%
3.49%
0.4
0.3
0.2
0.1
0.0
20
25
30
35
40
45
LA COMPATIBILITA’ tra due misure:
Esempio:
Determinare il livello di confidenza tra queste coppie di valori
x1±S1
x2±S2
25 ±1.3
40 ±1.3
25 ±1.3
30 ±1.3
t
40 25
1.32 1.32
30 25
1.3 1.3
2
25 ±1.3
28 ±1.3
2
28 25
1.3 1.3
2
25 ±1.3
40 ±1.3
2
40 25
1.3 7
2
2
15
8.1
1.84
5
2.72
1.84
P(t)
CL
>>99.999%
<<0.001%
99.35%
0.65%
3
1.63
1.84
89.96%
10.04%
15
2.11
7.12
96.51%
3.49%
0.4
0.3
0.2
0.1
0.0
20
25
30
35
40
45
LA COMPATIBILITA’ tra due misure:
Determinare il livello di confidenza tra queste coppie di valori
Esempio:
x1±S1
x2±S2
25 ±1.3
40 ±1.3
25 ±1.3
30 ±1.3
t
40 25
1.32 1.32
30 25
1.3 1.3
2
25 ±1.3
28 ±1.3
2
28 25
1.3 1.3
2
25 ±1.3
40 ±7
1.3 7
0.4
0.3
0.2
0.1
0.0
30
40
2
40 25
2
20
50
60
2
15
8.1
1.84
5
2.72
1.84
P(t)
CL
>>99.999%
<<0.001%
99.35%
0.65%
3
1.63
1.84
89.96%
10.04%
15
2.11
7.12
96.51%
3.49%
Rappresentazione grafica:
x1±S1 25 ± 1.3
20
25
30
x2±S2=40 ± 1.3
35
40
45
I punti sono come
gaussiane viste
dall’alto dove la barra
di errore corrisponde
ad una deviazione
standard
40
35
30
25
Misura 1
Misura 2
Rappresentazione grafica:
x1±S1 25 ± 1.3
x2±S2=30 ± 1.3
20
25
30
40
35
30
25
Misura 1
Misura 2
35
40
45
Rappresentazione grafica:
x1±S1 25 ± 1.3
x2±S2=28 ± 1.3
20
25
30
40
35
30
25
Misura 1 Misura 2
35
40
45
Rappresentazione grafica:
x1±S1 25 ± 1.3
x2±S2= 40 ± 7
20
30
40
50
45
40
35
30
25
Misura 1
Misura 2
50
60
FORMULE ED ELEMENTI DA RICORDARE -1
errore (assoluto): x
errore relativo:
media aritmetica: x
xi
i 1 N
(x x)
i 1
x
x
N
i
2
dev. standard
della media: S x
( N 1)
propagazione degli errori:
f ( x1 , x2 ,....xN )
somma e differenze:
prodotti e rapporti:
x
errore%: 100
N
N
dev. standard: S x
x
f ( x1 , x2 ) K x1 x2
a
b
(x x)
i 1
2
i
N ( N 1)
Sx
N
FORMULE ED ELEMENTI DA RICORDARE -2
f ( x)
Gaussiana:
compatibilità: x1 S1
t
media pesata:
X best
N
xi
2
i
e
2 2
(significato dei parametri e uso
della tabella delle probabilità)
; x2 S2
S S
2
1
2
2
P(t ) CL 100 P(t )
errore sulla media pesata:
X
best
1
i 1
2
x1 x2
i 1
N
1
x 2
2
i
rappresentazione dei risultati FINALI con il corretto numero di
CIFRE SIGNIFICATIVE
1
N
1
i 1
2
i










