M. Salerno
Kirchhoff
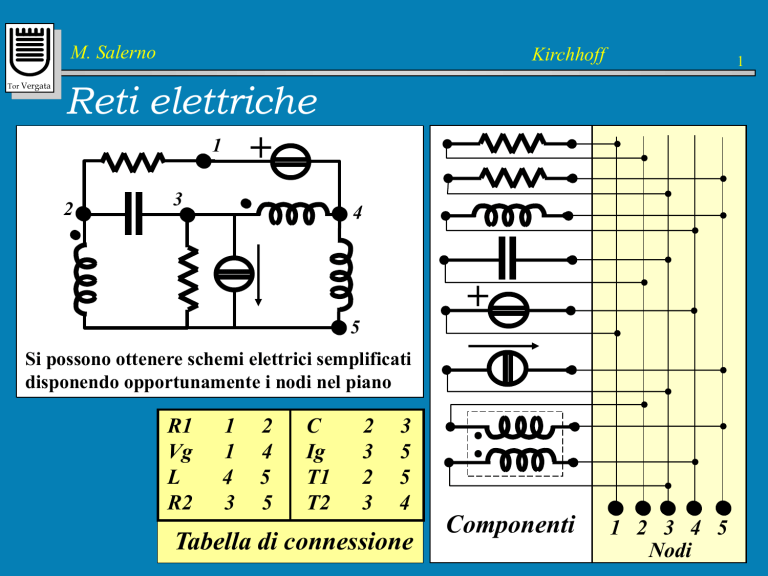
Reti elettriche
La
tabella
di
connessione
descrive
1 di
Una
rete
consiste
in una è spesso
Ogni
rigaelettrica
della
connessione
è
L’insieme
dei
filitabella
di
connessione
+
completamente
la rete
e viene
impiegata,
opportuna
di un
insieme p.es.,
detta
ramoconnessione
della
rete
1
Tor Vergata
detto schema di cablaggio. Tale schema è
nei
sistemi di
analisi
automatica.
prefissato
diper
componenti
3ogni
spesso
montaggio
Si
ha2unutile
ramo
perl’effettivo
componente
bipolare
4 del
circuito.
Si
2elettrica
ramiche
perèrete
ogni
componente
2-porte
Ahanno
Una
volte
reteinvece
ottenuta
elettrica
assegnando
si utilizza
la
Le
reti
elettriche
possono
essere
estremamente
Tuttavia
schema
di cablaggio è spesso di
locuzione lo
circuito
elettrico.
complesse.i componenti ,
difficile
lettura.
Nel presente
contesto
le due
locuzioni sono
Esempi:
i nodi
della
rete
e possono
P.es., nei circuiti
integrati
si
avere reti
quasi
sinonimi.
Ilcon
ramo
L
4
5
corrisponde
all’induttore
la ditabella
di connessione
milioni
componenti
e centinaia di
5
Ciò non è vero in generale.
migliaia di nodi
ISi
rami
T1ottenere
2 5 di 7schemi
possono
elettrici
Esempio:
rete
componenti
e 5semplificati
nodi
T2
3
4
corrispondono
al
trasformatore
disponendo opportunamente i nodi nel piano
R1
Vg
L
R2
1
1
4
3
2
4
5
5
C
Ig
T1
T2
2
3
2
3
3
5
5
4
Tabella di connessione
Esempi
In elettronica si dice circuito
elettronico e circuito integrato, ecc.
In telecomunicazioni, si dice circuito
telefonico, circuito a due o a quattro
fili, circuito di giunzione, per indicare
singole connessioni operative.
Invece, rete telefonica indica
l’insieme dei circuiti usati in un certo
ambito (p. es., rete telefonica
interurbana).
+
In impiantistica, si dice rete elettrica
di trasmissione o di distribuzione.
Componenti
1 2 3 4 5
Nodi
M. Salerno
Tor Vergata
Kirchhoff
2
Grafo di una rete elettrica
Il grafo di una rete elettrica è uno schema di
connessione che prescinde dai componenti usati
Nel grafo non sono indicati i componenti, ma
solo i relativi rami, rappresentati da segmenti
Ramo orientato
Esempio
1
a
+
b
3
2
g
e
h
d
f
5 nodi
Per semplicità il segno della rami
-1 0indicato:
0 0 a
tensione non1 viene
-1 0 0 1 0 b
Ramo k-esimo
0 0 0 -1 1 c
v0 k -1, ik d
0
0
1
C =
Scegliendo 0per1ogni
e
-1 ramo
0 0un verso
arbitrario si0 ottiene
0 -1 il 0 1 f
grafo orientato
0 0 o 1 -1 0 g
0 1 0 della
0 -1reteh
schema topologico
1
4
c
5
Grafo
Grafo
orientato
Rete
elettrica
IMatrice
rami deldi
grafo
sono identificati
connessione
[C ] ,
con
lettere o conRnumeri
di dimensioni
xN
R ramo
= numero
dei rami
Percon
ogni
occorre
considerare
N = numero
dei nodi
una tensione
e una corrente.
Per
è usata
la dal nodo j
Cij =tutti
-1 serami
il ramo
i esce
convenzione
delle potenze
entranti:
= 1 se il ramo
i entra nel
nodo j
= 0 altrimenti+
Ramo k-esimo
Esempio: R = 8 ; N v
=k5, ik
[ ]
2
3
4
M. Salerno
Tor Vergata
Kirchhoff
Leggi di Kirchhoff
Dato il grafo orientato di una rete, è possibile
scrivere le leggi Kirchhoff
Legge di Kirchhoff alle tensioni:
La somma algebrica delle tensioni presenti
su una maglia della rete è uguale a zero
Esempio
1
a
b
3
2
g
e
h
d
f
4
c
5
Grafo
orientato
Maglia
Maglia
abge
abge
hed
Maglia
abge
gcd = abcde
+; gcd
Il
numeroun
delle
leggidi
dirami
Kichhoff
Maglia:
insieme
che
che
si possono
scriverechiuso
è molto
individua
un percorso
elevato
Verso di maglia: l’ordine di
Le equazionidel
chepercorso
si ottengono
non
percorrenza
chiuso
sono fra loro indipendenti
Il segno della tensione è positivo
Esempio :semaglia
(negativo)
il verso di ramo
coincide
(non+coincide)
abge V
Vb + Vgcon
+ ilVverso
a
e=0
di maglia
gcd
- Vg + Vc + Vd = 0
Esempi
Il ramo g è percorso dalle due
Maglia
abge
maglie
conhed
verso opposto.
Sommando
membro
a membro, si
Verso
orario
Verso di
di maglia:
maglia:
orario
haLegge
Legge di
di Kirchhoff
Kirchhoff alle
alle tensioni
tensioni
Va + Vb + Vc + Vd + Ve = 0
V
- VVeb–+VVd g=+0Ve = 0
Vha +
che è l’equazione alla maglia abcde
3
M. Salerno
Tor Vergata
Kirchhoff
Leggi di Kirchhoff
Dato il grafo orientato di una rete, è possibile
scrivere le leggi Kirchhoff
Legge di Kirchhoff alle correnti:
La somma algebrica delle correnti,
che attraversano un taglio della rete,
è uguale a zero
Esempio
1
a
b
3
2
gg
ee
h
d
f
4
c
c
5
Grafo
orientato
; aeh= gceh
Taglio
Taglio
agc agc
hdfgb
aeh
egfd
hdfc
agc
+ aeh
Il
numero
leggididirami
Kichhoff
Taglio:
undelle
insieme
che
che
si possono
è molto
divide
la rete inscrivere
due parti
non
elevato
connesse
Le molti
equazioni
si ottengono
non
Esempi
In
casidiche
un
taglio
separa
un
Nella
legge
Kirchhoff,
il
segno
sono
fra
loro
indipendenti
solo
da tutti
gli altri
dellanodo
corrente
è positivo
Esempio:hdfgb
taglio
Taglio
(negativo) se il verso di ramo è
Esempi
Se
rami
agcsi tagliano
Ia i–concorde)
Ig – individuati
Ic =con
0 il
concorde
(non
dal taglio,
le sottoreti relative ai
verso
del taglio
aeh
+ nodi
Ie + [4,
Ih =
Taglio
aehIea ai
egfd
nodi [3,2,1]
5] 0
Esempi
risultano
separate
Il ramo
appartiene ai due tagli
Verso
delataglio:
Taglio
egfd
agc
Taglio
hdfc
con
verso
opposto.
Sommando
dal
dai
nodo
nodi
[2,1,4,5]
[2]
ai
nodi
al nodo
[1,
3, [3]
4, 5]
Si
può
assegnare
un
verso
Verso
del
membro
membro, si ha
Verso
delataglio:
taglio:
convenzionale
alaltaglio,
p.
es.,
dai
al
nodo
[2,3,5]
nodo
[1,[3]
4]
dai nodi
nodi [2,1,4,5]
[2,3,1,4]
al
nodo
[5]
I
–
I
+
I
+
I
=
0
dai nodig[4, 5]
[3,2,1]
c ai nodi
e
h
–ffdel
I+c taglio
I=dc 0= 0gceh
eh I–a I–gd I+g I
che-èIl’equazione
-I +I -I +I =0
4
M. Salerno
Tor Vergata
Kirchhoff
Leggi di Kirchhoff
Le leggi di Kirchhoff valgono
dipendono
neldal
dominio
grafo del
del circuito,
tempo.
Essendo equazionima
lineari,
non dipendono
algebriche,dai
a coefficienti
componenticostanti,
presenti.valgono anche
Due
in
qualunque
circuiti diversi,
dominio
aventi
trasformato,
lo stesso grafo,
definito da operatori lineari.
soddisfano le stesse leggi di Kichhoff.
I domini di interesse nella analisi delle reti sono:
dominio del tempo, grandezze elettriche vk(t) , ik(t)
Le leggi di Kirchhoff si esprimono in generale nel modo seguente:
dominio dei fasori, grandezze elettriche V k , I k (per il regime permanente)
S
0 ; S bk Ik = 0 con k = 1, … R e ak e bk pari a +1, -1, 0
k ak Vdi
k=
dominio
Laplace,kgrandezze
elettriche Vk (s) , I k (s)
R: numero dei rami
(si ha coefficiente zero quando una corrente o una
esprimono,
tensione non appare in una certa legge di Kirchhoff)
Le leggi di Kirchhoff si
nei domini del tempo, dei fasori e di Laplace,
nello stesso modo e con gli stessi coefficienti ak e bk :
Le leggi di Kirchhoff si esprimono con equazioni
S
Sk bk ik(t) = 0
(dominio del tempo)
k ak vk(t) = 0 ;
lineari,
S
= 0di operatori
;
Sdifferenziali)
(dominio dei fasori)
algebriche
k ak V k (prive
k bk I k , = 0
omogenee
(prive di termini noti)
S a V (s)
=0;
S b I (s) = 0
(dominio di Laplace)
k
k
k
k
k k
5
M. Salerno
Tor Vergata
Kirchhoff
Albero, coalbero
Determinazione
dell’Albero
e delindividuare
Coalbero :
Per
l’analisi di una
rete, occorre
Si tolgano alcuni rami dal grafo, in modo che:
Un insieme indipendente
non sia più presente nessuna maglia
di Leggi di Kirchhoff alle tensioni
il grafo rimanga connesso
Un insieme indipendente
Insieme dei rami residui: albero
di Leggi di Kirchhoff
alle correnti
Insieme dei rami tolti:
coalbero
RA = 4 ; RC = 4
Esempio
1
b
a
3
2
g
e
h
d
Albero: abcd
bcgh
Albero:
abef
bcdh
Albero:
Si
Sitolga
tolgaililililefgh
ramo
ramoadfe
Si
tolga
ramo
Si
tolga
ramo
Coalbero:
aefd
Coalbero:
cdgh
aefg
Coalbero:
f
4
c
5
Esempio
Un insieme
indipendente
RAlcune
: numero
dei rami
coppie
albero
/ coalbero
N
:
numero
dei
nodi
di Leggi di Kirchhoff è tale che:
Rami
residui:
Rami
residui: abcdefgh
bcdefgh
bcdfgh
bcdgh
bcgh
Albero:
nessuna
Legge
Rami
tolti:
nessuno
R
numero
dell’albero
Rami
tolti: dei
aramiappartenente
ae
aef
aefd
A : Coalbero:
all’insieme è combinazione
RCpuò
: numero
dei
rami delramo
coalbero
Si
togliere
qualsiasi
Si
può
togliere
qualsiasi
ramo
,
Non si può togliere
più
delle
altre
Albero:
bcdh
Nel
caso
generale,
eccetto
il
ramo bh
b risulta:
alcun
ramo
i rami
Coalbero:
aefg
ogni
ulteriore
(altrimenti
il nodo
1 nonLegge
è più è
R
= N – 1delle Leggi
combinazione
connesso
alAresto del grafo)
Albero:
abefall’insieme
appartenenti
RC = R cdgh
–N+1
Coalbero:
Un numero
di ramiinsiemi
pari a N-1 permette
Per
individuare
Albero:N nodi,
abcd
di connettere
senza dare luogo
indipendenti di Leggi di Kirchhoff,
ad alcuna maglia
Coalbero:
efgh
il grafo
orientato
della rete viene
Nel caso dell’esempio
suddiviso
in
Ai
RAfini
=sottografi
Ndella
– 1 =presente
4 ;complementari,
RC =trattazione
R–N+1=4
due
tutte le coppie albero / coalbero
[ in generale
non
RA = RC ]
detti
Albero
e risulta
Coalbero
sono
equivalenti
6
M. Salerno
Tor Vergata
Kirchhoff
Leggi alle tensioni
Espressione
generale
dell’insieme
Se
si aggiunge
all’albero
un ramo
indipendente
di Leggi
del coalbero,
si ottiene
una di
maglia
Kirchhoff alle tensioni
Tale ramo è detto
[VC ] +ramo
[ Adi ]chiusura
[ V A ] = [0 ]
Esempio
[VC ]
[VA ]
2
RA = 4 ; RC = 4
1
vettore
a colonna delle b
tensioni del coalbero
3
4
vettore
g
e colonna delle
tensioni dell’albero
f
c
d
[ A ] hmatrice di RC righe e
5
Albero: abcd RA colonne
con elementi pari a +1 , -1 , 0
Coalbero: efgh
Esempio
LeggeediV
Si aggiunga
Ve il ramo
a
maglia V
KirchhoffV
b
[VSi ottiene
] = fla ;maglia
[V ] =eabcd
C
A
Vg
V
(e ) VVe + Va + Vb + Vc +VVc d = 0
Il ramo Vdi
h chiusura fissa:
d
(f )
f + Vd = 0
il verso della maglia,
(g ) 1Vg –1 Vc1– V1d = 0
il nome
0 0della
0 1maglia.
[ (h
A ])= Vh + Va + Vb + Vc = 0
0 0 -1 -1
di
1 Insieme
1 1 indipendente
0alle tensioni
Legge di Kirchhoff
coalbero
albero
Leggi
di Kirchhoff
alle tensioni
alla maglia (e)
equazioni sono
indipendenti,
Usando Le
le notazioni
matriciali
V
+V
0
perché
ognuna
dibesse
contiene
termine
e+V
a+V
c + Vun
d=
Ve
1(tensione
1 1 del1ramo
Vadi chiusura)
VQuesta
0procedura
0 non
0 1presente
Vbessere
nelle altre
f
può
+
= [0 ]
Vgripetuta
0 per
0 -1ogni
-1 ramo
Vc del
Vh
1 1 1 0 Vd
coalbero
7
M. Salerno
Tor Vergata
Kirchhoff
Leggi alle correnti
Espressione
Se si eliminagenerale
un ramodell’insieme
dall’albero,
di
laindipendente
rete si dividediinLeggi
due parti
Kirchhoff
alle correnti
separate,
[IA che
] +definiscono
[B ] [ IunC ]taglio
= [0 ]
Esempio
[IA ]
[IC ]
2
RA = 4 ; RC = 4
1
vettore
a colonna delle b
correnti dell’albero
3
4
vettore
ee colonna delleg g
correnti del coalbero
f
c
d
[B ] hmatrice di RA righe e
5
Albero: abcd RC colonne
con elementi pari a +1 , -1 , 0
Coalbero: efgh
Esempio
Si elimini
a diIe
Ia il ramoLegge
taglio I
Kirchhoff
b il taglio aeh If
Si
ottiene
[I ] =
; [I ] =
C
Ic
I
(a ) I Ia - Ie - Ih = 0 Ig
h
Il ramoddell’albero
fissa:
Ib – Ie – Ih = 0
(b )
il verso del taglio,
(c ) -1 Ic0 – I0e +-1Ig – Ih = 0
-1 0 del
0 -1
Id - Ie - taglio.
I + Ig = 0
[B(d] =il) nome
-1 0 1 -1f
Insieme
di
Legge di -1
Kirchhoff
-1 1 indipendente
0alle correnti
albero
coalbero
Leggi
di Kirchhoff
alle correnti
A
per il taglio (a)
equazioni sono
indipendenti,
Usando Le
le notazioni
matriciali
Ia –diIesse
Ih = 0 un termine
perché ognuna
e – contiene
Ia
-1(corrente
0 0 del-1ramoIedell’albero)
IQuesta
-1procedura
0 non
0 -1
If essere
presente
nelle altre
b
può
Ic
Id
+
= [0 ]
-1
0
1
-1
I
g
ripetuta per ogni ramo
-1 -1 1 0 Ih
dell’albero
8
M. Salerno
Tor Vergata
Kirchhoff
Variabili indipendenti
Leggi di Kirchhoff alle correnti
tensioni
assegnate
assegnate
le tensioni
correnti
[
V
]
e
[
IC ]
A
[V ] = - [ A ] [ V ]
[[V
I[ICA C] ]==- -[ [A
BB]] ][[ [V
IIAC A]] ]
A
C
del coalbero,
dell’albero,
si possono
possono calcolare
calcolare le
le
si
si possono
calcolare
correnti
dell’albero
tensioni
del
coalbero
[VC ] e [IA ]
Correnti
Tensioni del
dell’albero:
coalbero:variabili
variabiliindipendenti
indipendenti
h
Ih
1
+
b
e
4
g
Iff
d
Vb
+
Ig
3
+
Ie
+
+
2
Va
+
+a
RA = 4 ; RC = 4
+
Esempio
Vc
c
Vd
5
Albero: abcd
Coalbero: efgh
Tensioni
Correnti
Rete di Kirchhoff
Tensioni
Poiché
Poichéiisoli
dei
solirami
rami
ramidell’albero
del
dell’albero
coalbero+
non
Correnti
nondefiniscono
definiscono
dei ramialcuna
alcun
del coalbero
maglia,:
taglio,
insieme
lelecorrenti
tensioni
di variabili
dei
deirami
ramiindipendenti
del
dell’albero
coalbero ,
che possono
possono
essere
essere
fissate
fissate
in modo
arbitrariamente
arbitrario
Le
Letensioni
correnti dei
dei rami
rami del
dell’albero
coalbero
Retenon
di sono
Kirchhoff
:
variabili indipendenti e
generatori
difissate
tensione
sui rami
non- possono
essere
arbitrariamente
dell’albero;
Rete
di Tensioni:
Correnti:
- generatori
di corrente sui rami
- generatori di tensione
sui rami
corrente
del coalbero.
dell’albero;
del coalbero;
La -Rete
di del
Kirchhoff
è lainsovrapposizione
rami
coalbero
aperti.
dell’albero
corto .
di una Rete di Tensioni
Le
deiRete
ramididel
dell’albero
Le correnti
tensioni
dei
rami
coalberosisi
e una
Correnti
calcolano con l’espressione
Una[Rete
Kirchhoff
analizzabile
I
]]di=
-- [[ B
] [èI
]
V
=
A
V
A
C
C
A
utilizzando esclusivamente le Leggi di
Tutte le tensioniKirchhoff
della rete sono nulle
Nella rete non circola alcuna corrente
9
M. Salerno
Tor Vergata
Kirchhoff
10
Teorema di Tellegen
Per una Rete di Kirchhoff,
si di
consideri
larete,
retemolte
ottenuta
permette
analizzare
delle reti,eccetto
a) da una
generica
noteproprietà
le disattivando
tensionitopologhe
deitutti
ramii generatori,
dell’albero
e le
didei
tensione
i-esimo
il generatore
corrente j-esimo
cioè proprietà
che
dipendono
dallaeconnessione
dei di
componenti,
La Rete di il generatore
correnti
rami
del
coalbero
La Rete di
Kirchhoff a) Aprescindendo
Bi j = 0 dalla natura dei componenti stessi Si ricordi che
ji =
Kirchhoff
in ogni
caso grafo, utilizzando
b)
da
reti aventi
lo stesso
Vipuò
sono
sidue
veda
essere
[T
VC=] =- -[[B
A ]][ VA ]
b) A
= -Rete
Bi j =per
1Tensioni
[
A
]
è
definita
ogni
grafo,
in
corrispondenza
a
ji
la
di
dalla
prima
rete
e
treottenuta:
casi
l’esempio
Aji = - Bij
[IA ]trasposizione
= - [ B ] [ IC ]
c) Aogni
=
B
=
-1
coppia
albero/coalbero
la
Rete
di
Correnti
dalla seconda rete
[.] T indica
ji
ij
h
Ih
1
Ie 3 3
e e
+ +
Ie
+
Vb
Ig
g
Iff
d
+
+
2
Va
+
++a
RA = 4 ; RC = 4
4
++
Esempio
+
V
Vcc
c
Vd
5
Albero: abcd
Coalbero: efgh
Rete di Kirchhoff
Le
di [ A[[]V
alle righe
a)colonne
b)
c)
Coppia
Coppia
Vcorrispondono
aac ;; IIeg]]
di [ B ] cambiate di segno (e viceversa)
Iltaglio
taglio aeh
aeh
IlIl
taglio
cegh,attraversa
attraversa
generatore
1 ;; 1 1 di
1 tensione,
la
ladefinito
maglia
magliadal
eacd
gcd
non attraversa
la0concordi
maglia
0 1 gcd ,
versi
versi
[didiAV]Ve =ec eVaV0 gdiscordi
definita dal generatore
di corrente
0 0 -1 -1
V
VVeg ===- V
0Vca 1 1 1 0
[
g
A
=
AAgc
==1-01
ea
ga
V
=
A
V
VVegg==- -AAeagcgaVV
-1
aca 0 0 -1
IIca ==
-I0]eIg= -1 0 0 -1
B
B
= 1- 1
a
-1 0 1 -1
Bcg
ae
ag = 0
IIca ==--BBcg
I
ae
a
ag Ige-1
g -1 1 0
M. Salerno
Tor Vergata
Kirchhoff
11
Teorema di Tellegen
Potenza
daottenuta
una reteda
di una
Kichhoff
a) Rete diassorbita
Kirchhoff
rete generica
Conservazione della potenza : S vk (t) ik (t)
= 0 ; S R pkT(t) = 0
T
Rami dell’albero SR pi = S R vi R
ii = [VA ] [IA ] = - [VA ] [ B ] [IC ]
A
A
b) Rete di Kirchhoff ottenuta da due reti aventi lo stesso grafo
: tensioni
T [ Aprima
Rami
del coalbero
S RC: pj = S RCS
vj ij v= [iVC=]T0 [ICvk] =
- [VA ]della
]T [Irete
Teorema
di Tellegen
C]
R k k
ik : correnti della seconda rete
S R vpotenza
i + Scomplessa
SApplicazioni:
v i = 0 conservazione
R v i =0
R
k k
S R pk = 0
[ A ]T
reciprocità delle reti
= valori
0 dei componenti
calcolo dellaSsensibilità
rispetto
RA pi + S
RC pj ai
A
i i
C
j j
=-[B]
R = RA + RC numero rami In una rete di Kirchhoff:
Somma prodotti tensione-corrente = 0
coalbero
albero
[somma su tutti i rami, stessa convenzione di segno]
Si ricordi che
[ IA ] = - [ B ] [ IC
][V ] = - [ A ] [V ]
C
A
[VC ]T = - [VA ]T [ A ]T
Somma potenze assorbite = 0
[somma su tutti i rami]
Suddiviso l’insieme dei rami in due sottoinsiemi, 1 e 2, complementari
[somma sul sottoinsieme 1]
Somma potenze assorbite =
= somma potenze erogate
[somma sul sottoinsieme 2]
M. Salerno
Kirchhoff
Sistema di equilibrio
Tor Vergata
Esempio
Analisi di una rete elettrica
12
Va = Ra Ia ; Vd = Rd Id resistori
QuantitàVnote
del del
problema
Incognite
Sistema
Incognite , 16Dati
funzioni
tempo:
generatoridi
b = Fb(t) ; If = Ff (t)
Costanti
Funzioniequilibrio
del tempo:
Va , Vb , Vdella
Ve , Vf , R
Vg rami
, Vh ; N nodi
Schema
c , Vd , rete:
R =R 8, R , LV ,=CL dIc
induttore
tensione impressa
I a , I b , I c , Id , I e , If , I g , I h
a
d
cc
ec
dt
equazioni
Leggi
alle
tensioni
R
tensioni
gen. tensione Fb(t) ;
tensioni
con pedici
Leggi
di e correnti R
componenti
N
+
1
equazioni
dVe corrente impressa
RapportoI =1:n
congruenti con quelli dei componenti
2R
C
condensatore
e
e
Kirchhoff
d
t
trasformatore Tg/Th
Ff (t) .
e secondo i versi indicati in figura
Leggi alle correnti
R correntigen. corrente
equazioni
Vh = n Vg
N – 1 equazioni
trasformatore
I
=
(1/n)
I
h
g
+ R
a
Tipo e valore
dei componenti
+ 3
2
Ce
Equazioni
di
1 +
Fb
R equazioni
+
2R
1 1 1 1 incognite
Va
Ve
Vf
0 0 0 1
4
+
Vg
0 0 -1 -1
Leggi di
+
Tg
Vh +1,1 -11 1 0
Kirchhoff : coeff.
+
Algebriche
lineari, omogenee,
Vb
Vc
Vd
= [0 ]
Kirchhoff
R=8
Ff
Lc
Ia
-1 0 0 -1 Ie
Rd
equazioni
Algebriche (circuiti senza memoria) e Idifferenziali
-1 0(circuiti
0 -1conImemoria)
b
f
Equazioni
+
+
+ Lineari (circuiti lineari) e non lineariI(circuiti
non
lineari)
-1 0 1 -1 Ig = [0 ]
5
c
dei componenti
Th
Id
-1 -1
Albero abcd ; coalberoTermini
efgh
noti (generatori o condizioni iniziali)
1 0
Ih
M. Salerno
Tor Vergata
Complessità
Complessità
Complessità differenziale
algebrica della
della
rete:
rete
Ca: Or
(ordine
della rete)
Ca = ordine algebrico del
sistema di equilibrio:
equazioni = numero delle incognite
Or = numero
ordine di
dell’equazione
differenziale risolvente:
dopo
sistema
numero ildei
rami )di
Si
ha opportuni
Ca 2passaggi
R ( R :algebrici,
Se
equilibrio si può ridurre a un’unica equazione
differenziale, il cui ordine è non superiore alla
Ca
= 2 Rdegli il
sistema
è detto
somma
ordini
dellerisolvente
equazioni del
sistema
……
equilibrio
Si ha sistema
Or NC generale
+ NL + 2 Ndi
M
….…( come nell’esempio, ove R = 8 e Ca = 16 )
Se
Ca
con NC = numero condensatori
NL = numero induttori
= numero
induttorièaccoppiati
<2R N
ilMsistema
risolvente
detto
…… sistema
analisi
Nell’esempio:
NC abbreviato
= 1; NL = 1; Ndi
M= 0
…… p. es.
analisi su
e pertanto
Or base
2 maglie
…… …… analisi su base nodi
(da conciderazioni più approfondite si può vedere
…… ……(descritte nel seguito)
che in questo caso si ha esattamente Or = 2)
Kirchhoff
Va = Ra Ia ; Vd = Rd Id
13
res.
Vb = Fb(t) ; If = Ff (t)
gen.
dIc
Vc= Lc
induttore
dt
dVe
Ie = C e
condensatore
dt
Vh = n Vg
Ih = - (1/n) Ig
trasf.
Ve
Vf
Vg
Vh
Ia
Ib
Ic
Id
+
1 1 1 1 Va
0 0 0 1 Vb
0 0 -1 -1 Vc
1 1 1 0 Vd
= [0 ]
+
-1 0 0 -1
-1 0 0 -1
-1 0 1 -1
-1 -1 1 0
= [0 ]
Ie
If
Ig
Ih
M. Salerno
Tor Vergata
Kirchhoff
14
Equazioni alle maglie: Res., Gen. tensione
dei coefficienti
Equazioni
alle maglie in rete
formadi
matriciale
Caso
elementare:
resistori
e generatori
termini
3.
Scrittura
delle equazioni alle
maglie
utilizzando
le incognitedi tensione
Imatrice
;
I
;
Ig ;noti
Ih
eelementi
f
diagonalefuori
principale
dalla
Ra+R
+Re correnti
Rd -di
Ra +R
Ie
-VR
2.
Scelta
coalbero
come
incognite
1.
coppia
albero
/(R
coalbero
c+Rddelle
c+Rd )
c
b : n. dei rami ; N : n. dei nodi
Maglia: e abcd
(Ra +Rc +Rd +Re ) Ie + Rd If
- (Rc +Rd ) Ig diagonale
+ (nessuna
R-V
+Rprincipale
a-V
c ) Ih = -Vb
I
;
I
;
I
;
I
b
f
b
Rd delle correnti
Re d f del- gcoalbero
Rd h
If
-Vnumero
2. Scelta
come0 incognite
incognite
:ddcR
–hgNe + 1
f
RaR
+R
Rc+R
+R
ac+R
d+R
R
I
+
R
I
R
I
= -Vf
Maglia:
f
d
tensione
impressa
R
+R
nessuna
R
R
+R
=
somma
resistenze
comune
La
matrice
d della
e
d f (verso:
d gin potenza
ca dcd dc dei
resistenza
totale
di
maglia
=
somma
delle
tensioni
sui
rami
resistivi
maglia
convenzione
entrante)
- Scrittura
(Rc+Rd ) delle- R
Rc+Ralle
-utilizzando
Rc
Ig
0 numero equazioni
: comune
R totale
–N+1
3.
equazioni
d
d+Rmaglie
g
resistenza
resistenza
fra
le +
maglie
e
/
g
somma
delle
resistenze
di
maglia
sulla
sulla
maglia
maglia
ef = 0
coefficienti
èhg
Maglia:
g
dc
(
R
+
R
)
I
R
I
+
(
R
+
R
R
)
I
R
correnti
correnti
I
I
e
e
I
I
concordi
discordi
c generatori
d
e
d f
c maglia
d
g(convenzione
g
c Ih
eee tensioni
hfg
somma
delle
impresse
dai
presenti
sulla
potenza uscente)
solo
le
incognite
introdotte
al
punto
2
R
+R
0a
- Rc
Ra+Rc+Rh Ih
-Vb Complessità
maglia
maglia
g/eIfcomune
verso
discorde
arami
c comuni
maglie
maglie
efesistema:
//h
h
gf= sempre
sui
sul
ramo
comune
c
edd
c
del
resistenza
in
comune
somma
resistenze
in
caso
Maglia:
h
abc
(
R
+
R
)
I
R
I
+
(
R
+
R
+
R
)
+
+
apositivo
c
e
c g
c
h
verso
discorde
Rfra
– averso
N
+segno
1concorde
<<hnegativo
2R
simmetrica
Metodo
segno
segnomatrice
negativo
positivo
attuale
fra
le
maglie
e
/
f
le
maglie
e
/
h
abbreviato
di
analisi
vettore
delle
incognite
deisegno
coefficienti
vettore
dei
termini
noti
V
b
Esempio
Ra
b
a
Vb
+
+
Re
Rh
eIe
+
Rg
+
Rd
+
Vf
+
d
Rc
gI
g
fIf
Ihh
Albero: abcd ; Coalbero: efgh
c
M. Salerno
Tor Vergata
Kirchhoff
15
Equazioni alle maglie : gen. di corrente
a) Scrittura
b)
c)
Identificazione
delle equazioni
della
rete di
alle
RTvincolo
maglie
per la rete
RTgeneratori
Reti
senza memoria
: resistori,
trasformatori
ideali,
Il sistemacontrollati,
diaequazioninullori
è risolubile
Ibb
generatori
di tensione, generatoriEquazioni
di
percorrente
la rete RT,
quale le tensioni
b1)
b3)
Scelta
Equazioni
coppia
allealbero
maglie
/ coalbero
Sostituire
i generatori
di corrente
dinella
vincolo
Equazioni
alle
maglie
g
e
Vx1 e Vx2 sono
termini
noti, mentre
b2)
Identificazione
delle
correnti
dei rami
del coalbero
assenti:
componenti
reattivi
(induttori,
condensatori,
induttori
accoppiati)
con
generatori
di
tensione
fittizi
I + I =-I
b (R +R ) I - R I = -V - V
tutte
le correnti
sono incognite.
b
c
g2
e
b
e h
g1
x2
I
nomi
e
i
versi
delle
correnti
dei
rami
del
fIg1 V Icc
Analisi
(Rcsu
+Rbase
) Ic -maglie
Rd +Ig1 - Rd IAih generatori
= - Vx2 di tensione fittizi,
c Simbolo
conviene
dareinvece
d
Per
la
rete
data
le
tensioni
d
x1
coalbero sono arbitrari. Tuttavia nel caso
h n. 5
Equazioni
dei
nomi
abbinati
ai
nomi
dei
generatori
di
di Resistori e generatori
Tensione (rete RT)
e Vx2 sono di
incognite.
Ic +a)
RdIdentificazione
Ig1 +Ig1Rd, già
Ih =presente
Vdix1unanelrete
g1 Rddella
corrente
circuito
I
Vx del sistema
Incognite
n.
5:RT
corrente
sostituiti
e dei
versi
coordinati
(p.
hes.
b)
Scrittura
di
equazioni
alle
maglie
per
la
rete
iniziale,
conviene
conservare
il
nome
e
il
Occorre
scrivere
ulteriori equazioni
- Re Ieb verso
+ Rd arbitrari
Ic + Rd Ig1 + (secondo
Rd+Re la
+Rconvenzione
h Nome
h ) Ih = 0 delle potenze
uscenti)
I
;
I
;
I
; Vx1corrente
; Vx2
b
c
h
verso c)
precedentemente
indicato
relativeAlbero:
ai generatori
adeg ; di
Coalbero:
bcfh
Scrittura delle
equazioni di vincolo
Es. n° 1
a
Ra
+
Rh
Vx2
+
Vx1 +
Re
Rd
Il
Per
il RT
generatore
di corrente
Iag2fini
non
Imaglie
non
compare
occorre
nelle
Rete
Il generatore
sistema
risolvente
su base
del
circuito
La
rete
RT,
introdotta
non
g1 didattici,
Radi corrente
V
g1 una +
+Infatti
alcuna
equazioni
equazione
scritte.
Occorre
di vincolo.
allora
scrivere
è l’insieme
delledisegnata.
equazioni
alleè sufficiente
maglie
viene
di
solito
riconoscerediche
equazione
vincolo.
nel sistema
di equazioni
alle
le equazioni
di vincolo
maglie
il termine
Ig1 é una
nota,+
Infatti,
introdotte
le incognite
I generatori
di corrente
sul quantità
coalbero
I
b
mentre
Vx1 è un’incognita.
semplificano
il sistema, sull’albero complicano
Vg1
Ig2
Ig1
Rc
ausiliarieRVex1 e Vx2 , le equazioni
Vx2alle
I
+
c
il sistema
per
l’aggiunta
di che
equazioni
di vincolo
Questa
osservazione,
semplifica
la
maglie
e le Iequazioni
di
vincolo
g2
R
soluzione
del
sistema,
deriva
dal
fattodella
Rc
Nella
scelta
della
coppia
albero
/ coalbero,
èche
h
R
possono essere dscritte
sulla
base
V
x1
il generatore
corrente
conveniente
scegliere, sedipossibile,
unIg1albero
sola
rete
iniziale.
Risulta
I
+
I
=
I
che non passi
per bi generatori
di g2
corrente
é posto
sulccoalbero.
M. Salerno
Tor Vergata
Kirchhoff
16
Equazioni alle maglie : trasformatori ideali
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
alle
RTvincolo
maglie per la rete RT
Analisi
sudelle
base
maglie
Il sistema
diaequazioni
è risolubile
Per
ilil generatore
di corrente
Ig1labInon
Per
trasformatore,
si ricordi
b
per la rete
RT,
qualedileevincolo,
tensioni
b1)
b3)
Scelta
Equazioni
coppia
allealbero
maglie
/ coalbero
occorre
alcuna
equazione
Sostituire
il generatore
di corrente
Equazioni
dinella
vincolo
Equazioni
alle
maglie
definizione
del
componente
le
Ig g
e sono
a)
Identificazione
della
rete
di
Resistori
e
generatori
di
Tensione
(rete
RT)
V
,
V
e
V
termini
noti.
poiché
si
trova
su
un
ramo
del
x1
gconvenzioni
h
relative
di segno
b2) Identificazione
delle correnti deiAirami
del coalbero
ebi rami
del
trasformatore
generatori
di
tensione
fittizi,
conviene
dare
V
=
n
V
(Ra+Rc ) Ib - Rc Ig = Vg1 - Vh
g
h Ie
coalbero.
Per
la
rete
data
con
generatori
di
tensione
fittizi
b)
Scrittura
del
sistema
di
equazioni
alle
maglie
per
la
rete
RTIle tensioni
nomi
abbinati
con il Inome del generatore
di IVg1x1f , Vg e
I
nomi
e
i
versi
delle
correnti
dei
rami
del
coalbero
sono
c
(Re+Rd ) Ie - Rd Ig1 + Rd Ig = - Vh
earbitrari.
2I + I )
IV1gh =sono
-1:n
(1
/con
n) la
(incognite.
invece
dcorrente
b
e
verso coordinato
Tuttavia, per la corrente Ig1 , giàcorrente
presente(con
nel circuito
h
c) Scrittura
di vincolo
+
Simbolo
- Rdconviene
Ie + Rdelle
Ig1 +-equazioni
Rd Igil=nome
Vx1
V2 =versi
n Vdi
g1
impressa)
e deiPer
rami
del +trasformatore
(con
iniziale,
e il verso
indicato.
la Occorre
1 vincolo
scrivere equazioni
dconservare
Incognite
n. 6
Equazioni
n.
6
V
V
2p.es.
1 generatore
congrui
con
i segni diper
riferimento,
positivo
conviene
utilizzare
della
potenza
il
diilcorrente
e
per
gcorrente
I
=
(
1
/
n
) Iil1
- Rc IIgb +
Rd Ie -V
Rxd Ig1 + la
(Rconvenzione
+
R
)
I
=
V
2
c
d
g
g
I).b ;Albero:
Ig ; Ieacdh
; Vx1; Coalbero:
; Vg ; Vh befg
dalla parte
del segno trasformatore.
entrante,
comearbitrari
nella definizione del trasformatore
ideale
Nome e verso
Es. n° 2
Ra
+
Th : Tg
=1:n
Re
Th
Vg1
Tg
Rd
Ig1
Rc
La
variabile
Ig appartiene
al coalbero
e quindi
Rete
RT risolvente
Il sistema
maglie del
circuitoè
Ra su base
V
g1 Non +
già
utilizzatadelle
nelle equazioni
maglie.
+alle alle
è l’insieme
equazioni
Ig maglie
così per la corrente Ihequazioni
, che deve essere
espressa
di vincolo
in funzione delle correnti del coalbero
+
Nello scrivere le equazioni di vincolo occorre
IbRe a non utilizzare
Ib +
VgIe (o
fare attenzione
+ Ih = correnti
Ie
+
Ihtensioni) del circuito che non siano già state R
RdequazioniValle
=maglie.
n Vh
utilizzate nelle
c
gV
V
x1
h
L’introduzione
di ulteriori variabili
Ig = equazioni.
- (1 / n) Ih
richiederebbe l’uso di ulteriori
M. Salerno
Tor Vergata
Kirchhoff
17
Equazioni alle maglie : gen. controllati
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
alle
RTvincolo
maglie per la rete RT
Analisi
sudelle
base
maglie
Il sistemaa di equazioni è risolubile
bIg1
per la rete RT,
cui le tensioni
b1)
b3)
Scelta
Equazioni
coppia
allealbero
maglie
/ coalberofisso e
Sostituire
il generatore
di corrente
Equazioni
diinvincolo
Equazioni
alle
maglie
g
Al
generatore
di
corrente
fisso
conviene
e
a)b2)
Identificazione
della
rete
di controllati
Resistori
e generatori
dix1 Tensione
(retetermini
RT)
V
, Ve e Vf sono
noti.
Identificazione
delle
correnti
dei rami del
coalbero
ig1
rami
controllati
dei
generatori
fittizio
(Ra+Rc+Rh ) Ig1 - Rh Id - Rh If + (Rc+Rh ) Ig =abbinare un generatore
-Id - If + diIgtensione
=
Ig
con
di
tensione
fittizi
b) generatori
Scrittura
del
sistema
di
equazioni
alle
maglie
per
la
rete
RT
con
verso
coordinato
con
la
corrente
Per
la
rete
data
invece
le
tensioni
V
k RIdh(Ig1 - Id - fIIf + Ig c
-Rx1heIig1versi
+ (R
Rhrami
If - del
Rhcoalbero
Ig = - Vesono impressa. Per il =
dI nomi
delle
d+Rcorrenti
h ) Id + dei
generatore
Vx1 , hVe e Vf dsonocontrollato
incognite.f di
c)
Scrittura
delle
equazioni
di
vincolo
)
arbitrari.
Tuttavia,
già+indicate
nel
fSimbolo
tensione, conviene
lo stesso
-RhIg1
+ RhIdper
+ +Rlehcorrenti
If - RhIg1Ig e=Ig- V
Vf = utilizzare
h Ig
e Vf
circuito iniziale, conviene conservare i nomi e i versi. nome e loOccorre
stesso segno
giàopportune
presenti nella
scrivere
Ve
g (Rc+Rh ) Ig1 - RVh xId - Rh If + (Rc+Rg +Rh ) Ih =rete
assegnata.
equazioni
vincolo.
Albero:diaceh
; Coalbero: bdfg
Nome e verso arbitrari
Es. n° 3
Ra
Ig
Ie =
k Vh
Vf =
h Ig
Ig1
Rh
Vh
+
Rg
+
Ie
Rd
Vf
Rc
Rete
di corrente Ieg1 : non
occorre
Per il RT
generatore controllato
k Vh
e6=
V
Incognite n.I+
Equazioni n.R6a
x1 su
alcuna equazione diIvincolo,
poiché
si
trova
-; hV
I(dI-g1
I
+
I
-I Id;-IIIfe ;+I Ig; =Ve k=R
I
I
; Vf d g f + Ig )
d delfcoalbero.
un
Le ramo
grandezze
Ie ge Vhx1non esono futilizzate nelle
= Rh(VIg1esse
-=Ih
+Vh Pertanto
Idil generatore
Ig1alle
f +I Ig )
If maglie.
Per
controllato
:- IVddevono
equazioni
f
f
g
If
R
I
Equazione
di
vincolo
essere
h
g espresse in funzione delle variabili già
Rg
VeV e I sono
+
Poiché
le
variabili
già
utilizzate
utilizzate.
Vh
f
g
I
I
+
I
=
k
R
(
I
I
I
d
f
g maglie
h g1
d
f + Ig )
nelle equazioni
alle
la seconda
Rd non deve essere
Vf modificata
Rc
+
hIvincolo
IR
equazione
ddi
g
M. Salerno
Tor Vergata
Kirchhoff
18
Equazioni alle maglie : nullori
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
alle
RTvincolo
maglie per la rete RT
Analisi
sudelle
base
maglie
Il sistemaa di equazioni è risolubile
bIb
per la rete RT,diinvincolo
cui Vf è
b1)
b3)
Scelta
Equazioni
coppia
allealbero
maglie
/ coalbero
Sostituire
il nullatore
con un
Equazione
Equazioni
alle
maglie
I
IRT)
e
e
ggnoto.
a)
Identificazione
della
rete
di
Resistori
e
generatori
di
Tensione
(rete
considerato
un
termine
b2)circuito
Identificazione
delle correnti
dei rami del coalbero L’unica equazione di vincolo
corto
e
il
noratore
con
b (Ra+Rc+Rh ) Ib + Rh Ie + Rc Ig = VIlg1nome e il verso della tensione sul noratore
unb)generatore
di tensione
fittizio
deriva
nullatore
per illaquale
del
sistema di
equazionisono
allearbitrari.
maglieÈper
la
RT
Perrete
ladal
rete
data invece
tensione
opportuno
considerare
f
c
Rd Id = - VIfnomi e i versi delle correnti
d Scrittura
dei
d
risulta
I
V
,
è
incognita.
h
d
separati i nodi 1 e 2 ,f a cui è connesso
il
c) Scrittura
equazioni
di vincolo
del
coalbero sono
arbitrari.
+
eSimbolo
Rh Ib + Rhdelle
Irami
=
V
e
f
ramo e , poiché sarà Occorre
necessario
Ie scrivere
= considerare
0 una opportuna
V
g Rc Ib + (Rc+Rg )xIg = Vf
la corrente su tale ramo.
equazione
vincolo.
Albero:diacfh
; Coalbero: bdeg
Nome e verso arbitrari
Es. n° 4
Ra
Vg1
+
+
Rh
Rd
8
Rete
RT
L’equazione
diRvincolo permette di eliminare
Vg1
a
l’incognita Ie dalle equazioni alle maglie.
Rg
Rc
1 Equazioni n. 42
e n. 4:
Incognite
Rg
+
Ib ; Id ; Ig ; Vf
Vf
Rd
Rh
Rc
M. Salerno
Tor Vergata
Kirchhoff
19
Equazioni ai nodi: Res., Gen. di corrente
coefficienti
Equazioni
ai nodi in forma
matriciale
elementi
fuori
dalla
Caso
elementare:
rete
resistori
e generatori
noti
3.
Scrittura
delle equazioni
aidi
nodi
utilizzando
le incognite di
E1corrente
;matrice
E2termini
; Edei
;
E
3 principale
4
diagonale
diagonale
principale
GdScelta
+G
-Ge di dei
0
-Gg incognite
E1
If
1.
di
nodo
riferimento
2.
nodi
come
Scelta
R : n. dei rami ; N : n. dei nodi
e+Gdelle
g untensioni
Nodo: 1
(Gd +Ge +Gg ) E1
- Ge E2
- Gnessuna
La
matrice
g-EII4bf b= Idei
f
nessuna
G
G
Ge come
Ga+G
+Gh - delle
Ga tensioni
0
E2nodi 0
2. -Scelta,
incognite,
dei
e
g
a
numero
incognite
:
N
1
e
G
G
+G
+G
+G
+G
+G
daGcG
eae g0gh è
E1 ; E2-;GEe 3E;1 E
coefficienti
Nodo:
2
+
(
G
+
G
+
G
)
E
G
E
=
4
corrente
impressa
a 1 eattraverso
h= 2i ramia resistivi
3
somma
delle
conduttanze
dei
uscenti
dal 0
nodo
Il0somma
segno
dei
conduttanza
presente
(rispetto
aldelle
nodo
di
riferimento)
- termini
Gcorrenti
G
E
E
I
numero
equazioni
:
N
-totale
1
a
a
33
b
sempre
conduttanza
resistori
connessi
al
nodo
1
nel
nodo
1
2
3
4
Nodo:
3 delle
-G
Egeneratori
=3
Ibe 4
relativi
a resistori
disposti
[somma
a delle]
2 + Ga E3di corrente
[somma
delle]
fra
i nodi
1
2
32 2R
3.
Scrittura
delle
equazioni
ai
nodi,
il
nodo
somma
correnti
entanti nel
nodo
1 eccetto
e impresse
dai
Complessità
del
sistema:
N
1
<<
simmetrica
-fra
Gg coppie di 0nodi è
0
Gc+G
E
I
nodo
3214- I
verso
verso
entrante
uscente
g
4
b
nodo
conduttanze
dei resistori
conduttanze
dei
resistori
caso
Nodo:
riferimento,
4
utilizzando
le
incognite
-segno
Gsolo
E
+
(
G
+
G
)
E
=
g positivo
1
c
4 negativo
abbreviato
di
sempre
negativo
connessi
fradei
i nodi
1 eMetodo
2 noticonnessi
frag segno
i nodi
1analisi
e 4b
attuale
vettore
delle
incognite
segno
sempre
negativo
matrice
dei
coefficienti
vettore
termini
introdotte al punto 2
Esempio
Ra
E33
E11
E22
E
44
equilibri di correnti, in funzioni di
Tale nodo viene indicato
grandezze che sono tensioni.
Rc
Pertanto occorre utilizzare sempre le
conduttanze
resistori
e cioè :le
E , E , Edei, E
indicano
Rg
Re
Rh
Attenzione!
È stato scelto come riferimento
Le
equazioni
il nodo
5 ai nodi esprimono
Ib
If
Rd
5
con il simbolo di massa
1
2
3
4
Gtensioni
Rc3,; 4G,d = 1 /
nodi
1,/ 2,
a = 1 / Rdei
a;G
c= 1
al ;nodo
di riferimento
R
Grispetto
de = 1 / R
e Gh = 1 / Rh
M. Salerno
Tor Vergata
Kirchhoff
20
Equazioni ai nodi : gen. di tensione
a) Scrittura
b)
c)
Identificazione
delle equazioni
della
rete di
ai
RCvincolo
nodi
per la rete RC
Il generatore
di
Vèg2risolubile
Per
il generatore
di tensione
Vnon
Reti
senza memoria
: resistori,
trasformatori
ideali, generatori
nullori
g1 non
Il
sistemacontrollati,
di tensione
equazioni
compare
nelle
equazioni
scritte.
occorre
alcuna
equazione
di vincolo.
generatori
di tensione, generatori
di
percorrente
la
rete RC,
quale
le Occorre
correnti
b1)
b3)
Scelta
Equazioni
nodo
nodi
riferimento
Sostituire
i generatori
di tensione
Equazioni
di nella
vincolo
Equazioni
aiaidi
nodi
allora
scrivere
una
equazione
di
vincolo.
Infatti
che
nelmentre
sistema
Ix1 basta
e Ix2 riconoscere
sono
terminiaccoppiati)
noti,
b2)
Identificazione
delle
tensioni
di nodo
assenti:
componenti
reattivi
(induttori, condensatori,
induttori
con
generatori
di
corrente
fittizi
E
Vg2
1 (Gd+Ge ) Vg1 - Ge E2 = Ig1 + Ix1
di equazioni
nodi
il termine
Vg1 è una
tutte
tensioni
sono
incognite.
3 -leE
4ai =
nomi
delle
tensioni di nodo sono arbitrari.
+
quantità nota, mentre
IV
x1g2è un’incognita.
Analisi
base
nodi
- GIsu
V
+
(
G
+
G
+
G
)
E
G
E
=
0
2 Simbolo
Ai2 generatori
di corrente fittizi,
conviene
dareinvece
e
g1
a
e
h
a
3
Per
le
rete
data
le correnti Ix1
Tuttavia nel caso della tensione Vg1 , già
Equazioni
n.
5
E
Eche
dei
nomirete
abbinati ai nomi dei
di Corrente
a) Identificazione
di una
generatori
di
RC)
4
e3generatori
Ix2 osservazione
sono incognite.
deriva (rete
dal fatto
3 - Gpresente
nela E
circuito
iniziale,
conviene di Resistori eQuesta
a E2 + G
3 =I Ix2
Incognite
n.es.
5:
tensione
sostituiti
e dei
versi
coordinati
(p.RC
xdel sistema
b)
Scrittura
di
equazioni
ai
nodi
per
la
rete
il
generatore
diulteriori
tensioneequazioni
Vg1 è
conservare
il
nome
indicato,
invece
di
Occorre
scrivere
Gc E4 = - Ig1 - Ix2
4 Nome
secondo
la
convenzione
delle
potenze
uscenti)
E
;
E
;
E
;
I
;
I
e verso
arbitrari
Risulta
Egeneratori
2 aial
3 - E44di=
x1V
introdurre
un nuovodelle
nomeequazioni di vincolo
relative
di
tensione
c) Scrittura
3nodo
g2x2
connesso
riferimento.
Ra
Es. n° 1
1
2
3 +
Ix2
4
Re
Rh
Vg2
+
Rd
Ix1
5
Vg1
Ig1
Rc
Ra suEbase
Il
risolvente
nodididattici,
Rete
RC RC,
Lasistema
rete
introdotta
a fini
Idel
3
x2
circuito
è l’insieme
non viene
di solitodelle
disegnata.
+
E2 equazioni aiVnodi
E4
g1
Infatti,
introdottedilevincolo
incognite
le equazioni
ausiliarie
IR
e Iscegliere
equazioni
ai
x2 , le
Ig1nodo
I generatori
dix1etensione
connessi
al
È opportuno
il nodo
Rd
Rc
h
nodi
e
le
equazioni
di
vincolo
diR
riferimento
semplificano
il
sistema,
di riferimento in che sia
quelli
non connessi
a tale nodo
Ix1 base
possono
essere
scritte
sulla
connesso
alla
maggior
partedi
complicano il sistema per l’aggiunta
della
sola retediiniziale.
dei
generatori
tensione
equazioni di vincolo
M. Salerno
Tor Vergata
Kirchhoff
21
Equazioni ai nodi : trasformatori ideali
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
ai
RCvincolo
nodi per la rete RC
Analisi
sudelle
base
nodi
Il sistema
di equazioni
è risolubile
Per
ilil generatore
di tensione
Vg1la
Per
trasformatore,
si ricordi
per la rete RC,
nella
quale lee correnti
b1)
b3)
Scelta
Equazioni
del ai
nodo
ainodi
nodi
didi
riferimento
Sostituire
il generatore
tensione
Equazioni
di componente
vincolo
Equazioni
definizione
del
le
V
+
g1
Identificazione
della
di Resistori
e generatori
(rete
RC)
Ix1 di
, IgCorrente
e Ih sono termini
noti.
relative
convenzioni
di segno
b2)
Identificazione
delle rete
tensioni
di Ai
nodo
e1a)
i rami
del
trasformatore
E
E
=
n
E
generatori
di
corrente
fittizi,
conviene
dare
1
4
2
(Gd+Ge ) E1 - Ge E2 = Ig1 - Ig
E
Per
rete
data invece
le correnti IE
3 ladel
con
di sistema
correntedifittizi
x14,
b) generatori
Scrittura del
equazioni
nodi per
rete
RC
nomiaiabbinati
con la
i nomi
generatore
di
I
I
IIg1g =e I-h1:n
(1
/ n)
I2
- Ih
2 - Ge E1 + (Ga+Ge ) E2 - Ga E3 = tensione
sono
incognite.
(con verso coordinato
con
lahtensione
di vincolo
l’equazione
di vincolo
lan seguente:
+
x= I
3c) Scrittura
Simbolo
- Ga E2 + delle
Ga E3Iequazioni
V2è=versi
Vdi
impressa) e dei rami E
del +trasformatore
(con
1 vincolo
Occorre
scrivere
equazioni
x1
E
=
V
3V
4 V g1
1 generatore
congrui con i segni diper
riferimento,
il
di4corrente
tensione
4 Gc E4 = - Ix1 + Ig
E3 2p.es.
- E
I=2 =V-g1( 1 e/ per
n ) Iil1
dalla parte
segno
).
trasformatore.
Nome e verso arbitrari
n. 6del
: E
Equazioni n.entrante
6 ; Incognite
1 ; E2 ; E3 ; E4 ; Ig ; Ih ; Ix1
Ra
Es. n° 2
3 +
1
2
Tg Ig
Ig1 Rc
Re
Ih
Th : Tg
=1:n
Th
Vg1
Ix1
Rd
5
4
Rete
RC risolvente
Ra su base
Il sistema
è
E3 nodi delIcircuito
x1
l’insieme delle
equazioni ai nodi +
Ig
equazioni
di vincolo
E1
E2
E4
Ig
Nello scrivere le equazioni di vincolo occorre
Re
fare attenzione a non utilizzare tensioni (o
Rd che non siano
Ig1 già stateRc
correnti) del circuito
E1 - Eai
= n E2
Ih
4 nodi.
utilizzate
nelle equazioni
L’introduzione di ulteriori variabili
I = - (1/ n) Ih
richiederebbe l’uso di gulteriori equazioni.
M. Salerno
Tor Vergata
Kirchhoff
22
Equazioni ai nodi : gen. controllati
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
ai
RCvincolo
nodi per la rete RC
Analisi
sudelle
base
maglie
sistemacontrollato
di equazioni
Per
Ie è: Irisolubile
Ie =il generatore
- kIl E
e = k Vh
2
per la rete RC,
cui le correnti
b1)
b3)
Scelta
Equazioni
del ai
nodo
ainodi
nodi
di riferimento
Sostituire
i rami
controllati
Equazioni
di invincolo
Equazioni
Le
grandezza
V
non
è
utilizzata
nelle
Per il generatore
controllato
a)b2)
Identificazione
della
di Resistori
(reteVRC)
Idi
If hsono
termini
noti.
f : Vf = h Ig
e eCorrente
Identificazione
delle rete
tensioni
di nodo e generatori
dei
generatori
controllati
equazioni
ai nodi.
IVe =e Però
Erisulta
1 (Gd+Gg ) E1 - Gg E4 = Ie + If
h = - E2
2sono V
Le
grandezze
I-gknon
utilizzate
f
con
di sistema
correntedifittizi
Scrittura del
equazioni ai nodi per
laequazioni
rete
PerRC
la rete
data invece le correnti
nelle
ai=nodi.
(Ga+Gh ) E2 - Ga E3 = - Ie
2b) generatori
E
h di
Gvincolo
Pertanto
l’equazione
èEla
Per il generatore
controllato
g (Edi
4 -corrente,
1)
Ie e If 1 sono
incognite.
Iequazioni
c) Scrittura
delle
di vincolo
x
Si
ha Vf utilizzare
= EI1e =
e Ilo
=EG2g (E
)
conviene
nome
e1lo
Simbolo
3
seguente
-g kstesso
- Ga E2 + G
4- E
a E3 = - Ig1
4
Incognite
stesso
segno
già presenti
nella
rete
Pertanto
l’equazione
è : n. 6
Equazioni
n.scrivere
6 di vincolo
Occorre
opportune
assegnata.
equazioni
vincolo.
EE1 1;=Eh2 di
;E
; 1Ie) ; If
G
3 ; 4E-4E
g (E
- Gg E1 + (Gc+Gg ) E4 = Ig1
Nome e verso arbitrari
Es. n° 3
Ra
Ie =
2
k Vh
Vf =
h Ig
Ig1
3
Ig
1
Rh Ie R
d
Vh
+
+
Rg
Vf
Ra
Rete RC
Rc
4
Ie
E2
Ig1
E3
Ig E
4
E1
Rg
Rh
Vh
+
Rd
If
Rc
M. Salerno
Kirchhoff
23
Equazioni ai nodi : nullori
Tor Vergata
a) Scrittura
b)
c)
Identificazione
equazioni
della
rete di
ai
RCvincolo
nodi per la rete RC
Analisi
sudelle
base
nodi
Il sistema di
di tensione
equazioni V
è g1
risolubile
Per il generatore
si ha
per la rete RC
in cui Ix1 e IN
b1)
b3)
Scelta
Equazioni
del ai
nodo
ainodi
nodi
di
riferimento
Sostituire
il nullatore
con
un circuito aperto,
Equazioni
di, vincolo
Equazioni
alle
maglie
V
g1
+considerate
Identificazione
della
di Resistori
e generatori sono
di Corrente
(rete
RC)
termini
noti.
b2)
Identificazione
delle rete
tensioni
di nodo
il a)
noratore
e
il
generatore
di
tensione
con
E
E
4
3 = Vg1
(
G
+
G
)
E
G
E
=
I
E
E
=
V
1
d
g
1
g 4
N
4
3
g1
E
E
4
generatori
di corrente
fittizi
Al3 generatore
direte
corrente
fittiziolerelativo
b) Scrittura
del sistema
di equazioni ai nodi per
la rete
RC
Per
la
data
invece
correnti
2 (Ga+Gh ) E2 – Ga E3 = 0
E
=
E
al generatore
1 conviene dare
Ix1 e di
IN2tensione
sono
incognite.
Per
il
nullatore
si
ha
c)
Scrittura
delle
equazioni
di
vincolo
I
nome e verso coordinati con quelli relativi
Simbolo
3
- Ga E2 + Ga E3 x= - Ix1
Incognite
n. 6
Equazioni
n.scrivere
6 Il nome
alla tensione
impressa.
e=il verso
Occorre
due
opportune
E
E
4 - Gg E1 + (Gc+Gg ) E4 = Ix1
2
1
E
Edi;1E
della
sono
arbitrari.
equazioni
vincolo.
E1 ;sul
E2noratore
2 corrente
Nome e verso arbitrari
3 ; E4 ; Ix1 ; IN
Es. n° 4
Ra
Rh
Rd
Ra
8
4
Ix1
E3
+
1
2
Rete RC
Vg1
3
E1
E2
Rg
E4
Rg
Rc
Rh
Rd
IN
Rc
M. Salerno
Tor Vergata
Kirchhoff
24
Analisi nel dominio dei fasori
Circuiti
Circuiti
senza nel dominio
Metodo
di analisi
deicon
fasori
memoria
nel
memoria
nel
dominio
Circuito in regime permanente: tutte le grandezze elettriche
dominio
dei fasori
del tempo
(tensioni e correnti)
del circuito sono di
tipo sinusoidale
Circuiti privi di condensatori,
Circuiti contenenti condensatori,
1. Determinare
il circuito
fittizio nel induttori,
dominioinduttori
dei fasori:
induttori, induttori
accoppiati
accoppiati
sostituireequazioni
tutte le grandezze impresse conequazioni
i rispettivi fasori;
determinare le impedenze (o le ammettenze) di tutti i
algebriche nel
algebriche nel
componenti reattivi
campo reale
campo complesso
2. Analizzare il circuito nel dominio dei fasori
L’analisi diL’analisi
circuiti con
di circuiti
memoria
connel
memoria
dominio dei fasori
3. Determinare i fasori delle grandezze d’interesse
è differente
è simile all’analisi
dall’analisididicircuiti
circuitisenza
senzamemoria
memoria
(eventualmente determinare le rispettive funzioni nel tempo)
ma implica calcoli
ed è molto
nel campo
complessa
dei numeri complessi
M. Salerno
Tor Vergata
Kirchhoff
25
Equazioni alle maglie : fasori
Viene
omesso il impresse
disegno della rete RT :
grandezze
Esempio alle maglie nel dominio dei Fasori
Equazioni
fasori delle
( jw
L(t)
+ 1=/ V
jwg1Ccos
) It ca+ j
+ R) I g1 - R I vg V
= 0g1 =
vg1
(w
a+R
al posto del generatore di corrente si
jj la presenza di un generatore
Vsupponga
g1 e
di tensione fittizio di tensione V x1
I g1 = Ig1 e jy
R iIg1ca(t)+=R Ig1g1 -cos
R I( vgw =t +
Vy
x1 )
Viene scelta una coppia albero /
- R I ca - R I g1 + ( 1 / jwCb + R ) I vg =Impedenze
V g1
coalbero, in modo che il generatore di
corrente sij trovi
Induttore
w Lsul coalbero. Le
correnti di maglia sono I , I , I
Condensatori 1 / j w Ca ; 1 /ca j wg1Cb vg
Non occorrono equazioni di vincolo,
poiché I g1 si trova sul coalbero.
Le incognite sono : I ca , V x1 , I vg
Dominio delalbero
tempo
coalbero
IC
caa
L
R
vg1(t)
I vg+
Ii g1(t)
g1
Dominio dei fasori
jwL
Cb
1
jwCa
R
V g1
+
+
I g1
V x1
1
jwCb
M. Salerno
Tor Vergata
Kirchhoff
26
Equazioni ai nodi : fasori
Viene
omesso il impresse
disegno della rete RC :
Fasori delle
grandezze
Esempio ai nodi nel dominio dei fasori
Equazioni
( jw
C(t)
1V
/ jg1wL
) E( 1w-t(+
1 /jjw) L ) E 2 = 0
vg1
cos
a +=
V g1 =
al posto del generatore di tensione si
jj la presenza di un generatore
Vsupponga
g1 e
di corrente fittizio di tensione I x1
-(1ig1
/ (t)
jwL=) IEg11 +cos
(1 (/ jwwL
G )+ jwCb ) E 2 -I g1 = Ig1 e jy
t ++ y
- jwCb V g1 = - I g1
Viene scelto un nodo di riferimento, in
-Attenzione:
jwCb E 2nello
+ ( 1scrivere
/ jwCble)equazioni
V g1 = Iaix1
nodi, è necessario considerare le
conduttanze
dei resistori
e le
Non occorrono
equazioni
di vincolo.
ammettenze
componenti
Le incognite
sonodei
: E
, E , I reattivi.
1
2
x1
di
Dominio delnodo
tempo
E1
L
vg1(t)
V g1
+
riferimento
Ca
ig1(t)
R
E2
Ammettenze
modo che il generatore di tensione si
trovi collegato
Induttore
1 / j awesso.
L Le tensioni di
nodo sono E , E , V
Condensatori j w 1Ca 2; j wg1 Cb
Cb
Dominio dei fasori
1
jwL
I x1
jwCa
G
I g1
V g1
+
jwCb
M. Salerno
Tor Vergata
Kirchhoff
27
Conservazione della potenza
In
permanente
Nelregime
dominio
del tempo
Conservazione
della
potenza
complessa
: :S R P
Conservazione
della
potenza
istantanea
Sc =v ½(t)Si R(t)V =k I0k* = 0
R
k
k
Somma
potenze
assorbite = 0 [somma su tutti i rami]
Essendo
P
=
P
+
j
Q
,
si
ha
:
c
a
Dimostrazione
Conservazione dellaSomma
potenza
attivaassorbite
: S R[daPtutti
½ S R Re
[V ki generatori
I k* ]=]0=
potenze
esclusi
a =i componenti
Scelta una coppia albero / coalbero, si definisca una rete di Kirchhoff prendendo
somma potenze
erogate
dai generatori
Somma
potenzei fasori
attive =assorbite
= 0 e sul
[somma
su [tutti
i rami] ] dei fasori delle correnti.
sull’albero
delle tensioni
coalbero
i coniugati
Applicando il della
teorema
di Tellegen,
si ottiene
e quindi
0
Conservazione
potenza
reattiva
: S SQ
½k*S= 0 Im
[V SIR *P ]=
R V=k I
c=0
R
Somma potenze reattive assorbite = 0
R
k
k
[somma su tutti i rami]
Reti RLC + generatori
Si ricordi che:
R
Pa > 0
Q
L
C
gen.
0
0
>=<0
0 > 0 < 0 >=<0
Somma potenze attive assorbite dai resistori ( > 0 ) =
= Somma potenze attive erogate dai generatori ( > 0 )
Somma potenze reattive assorbite dagli induttori ( > 0) +
Somma potenze reattive assorbite dai condensatori (< 0) =
= Somma potenze attive erogate dai generatori ( > = < 0)












