FLOWCHART
DELL’ALGORITMO DI
APPRENDIMENTO DELLA
RETE DI KOHONEN
ALGORITMO RETE DI KOHONEN
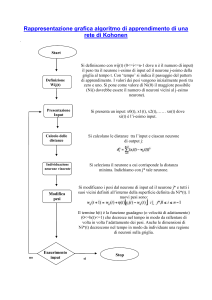
L’algoritmo di apprendimento di questo tipo di rete è il seguente:
1)
Si definiscono con wij(t) (0<=i<=n-1 dove n è il numero di input) il peso tra il neurone iesimo di input ed il neurone j-esimo della griglia al tempo t. Con ‘tempo’ si indica il
passaggio del pattern di apprendimento. I valori dei pesi vengono inizialmente posti tra
zero e uno. Si pone come valore di Ni(0) il maggiore possibile (Ni() dovrebbe essere il
numero di neuroni vicini al j-esimo neurone).
2)
Si presenta un input: x0(t), x1(t), x2(t),…… xn(t) dove xi(t) è l’i-esimo input.
3)
Si calcolano le distanze di tra l’input e ciascun neurone di output j:
d²j = Σ (xi (t) – wij(t)) ²
sommatoria da i=o a n-1
4)
Si seleziona il neurone a cui corrisponde la distanza minima. Indichiamo con j* tale
neurone.
5)
Si modificano i pesi dal neurone di input ed il neurone j* e tutti i suoi vicini definiti
all’interno della superficie definita da Ni*(t). I nuovi pesi sono:
wij(t+1) = wij(t) +ŋ(t)[ xi(t) – wij(t)]
i|_j*, 0<= i <= n
Il termine h(t) è la funzione guadagno (o velocità di adattamento) (0<=h(t)<=1) che decresce
nel tempo in modo da rallentare di volta in volta l’adattamento dei pesi. Anche le
dimensioni di Ni*(t) decrescono nel tempo in modo da individuare una regione di neuroni
sulla griglia.
6)
Si ripete tutto a partire dal punto 2).
INIZIO
1° passo
Fisso Wijt con j [o,n-1]
Definisco:
Ni(0) =max
Ni(0) <= i
Wijt [ 0,1 ]
2° passo
Ni(0) numero
neuroni vicino al jesimo neurone
Xi(t) input i-esimo
al tempo t
Presentazione input
X0(t)......Xn-1(t)
i >= n
Wij Peso tra il
neurone i-esimo di
input e il neurone jesimo della griglia al
tempo t
SI
STOP
NO
3° passo
Calcolo le distanze
n-1
dj2= (Xi(t)- Wij(t))2
i=0
Selez. il neurone di out j*
tale che
dj2 = min
Distanza tra i neuroni
di input e il j-esimo
neurone di output al
tempo t
Definisco:
h(t) [ 0,1 ]
h(t) = (1/n+1)(t) + 1
4° passo
h(t) funzione di
guadagno
h(t) decresce
Definisco i nuovi pesi
Wij(t+1)= Wij(t)+h(t) [Xit-h(t) ]
con i che va da 0 a n-1
Nuovi pesi