file

Parallelogrammi e trapezi
Definizione e proprietà del parallelogramma
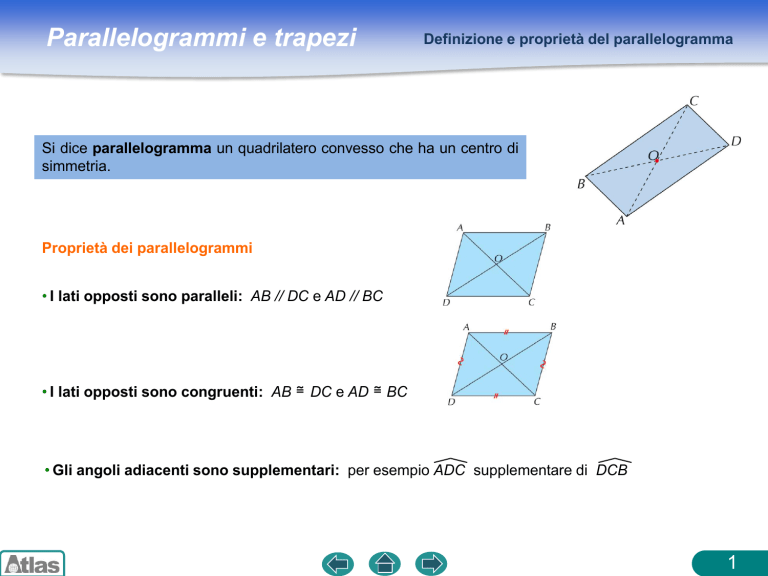
Si dice parallelogramma un quadrilatero convesso che ha un centro di
simmetria.
Proprietà dei parallelogrammi
• I lati opposti sono paralleli: AB // DC e AD // BC
• I lati opposti sono congruenti: AB ≅ DC e AD ≅ BC
• Gli angoli adiacenti sono supplementari: per esempio ADC supplementare di DCB
1
Parallelogrammi e trapezi
Definizione e proprietà del parallelogramma
• Gli angoli opposti sono congruenti: DAB ≅ DCB e ADC ≅ ABC
• Le diagonali si incontrano nel punto medio: AO ≅ OC e DO ≅ OB
Criteri per stabilire se un quadrilatero è un parallelogramma
Teorema. Un quadrilatero è un parallelogramma se:
ha i lati opposti paralleli oppure
ha i lati opposti congruenti oppure
ha gli angoli adiacenti supplementari oppure
ha gli angoli opposti congruenti oppure
ha le diagonali che si incontrano nel punto medio oppure
ha una coppia di lati opposti congruenti e paralleli.
2
Parallelogrammi e trapezi
Parallelogrammi particolari
Si chiama rettangolo un parallelogramma che ha tutti gli angoli
congruenti.
Gli angoli di un rettangolo sono quindi retti.
Un rettangolo ha tutte le proprietà dei
parallelogrammi ed inoltre:
un rettangolo ha le diagonali congruenti
Per stabilire se un quadrilatero è un rettangolo basta verificare che sia un parallelogramma e procedere
in uno dei seguenti modi:
 verificare che ci sia almeno un angolo retto
 verificare che le diagonali siano congruenti
3
Parallelogrammi e trapezi
Parallelogrammi particolari
Si chiama rombo un parallelogramma con tutti i lati congruenti.
Un rettangolo ha tutte le proprietà dei
parallelogrammi ed inoltre:
un rombo ha le diagonali che sono tra loro
perpendicolari e bisettrici degli angoli opposti.
Per stabilire se un quadrilatero è un rombo basta verificare che sia un parallelogramma e procedere in
uno dei seguenti modi:
 verificare che abbia due lati consecutivi congruenti.
 verificare che le diagonali siano tra loro perpendicolari.
 verificare che una diagonale sia bisettrice degli angoli cui si riferisce.
4
Parallelogrammi e trapezi
Parallelogrammi particolari
Si chiama quadrato un parallelogramma che ha tutti i lati congruenti e
tutti gli angoli congruenti.
Un quadrato possiede tutte le proprietà dei parallelogrammi e quelle dei
rettangoli e dei rombi, perciò:
le diagonali sono congruenti, sono perpendicolari, sono bisettrici
degli angoli cui si riferiscono.
Per stabilire se un quadrilatero è un quadrato basta verificare che sia un parallelogramma e procedere in
uno dei seguenti modi:
 verificare che ci siano due lati consecutivi congruenti e che ci sia un angolo retto.
 verificare che le diagonali siano congruenti e perpendicolari.
 verificare che le diagonali siano congruenti e che una di esse sia bisettrice degli angoli cui si riferisce.
5
Parallelogrammi e trapezi
Parallelogrammi e isometrie
Per definizione tutti i parallelogrammi hanno un centro di simmetria.
I parallelogrammi che possiedono assi di simmetria sono:
 il rettangolo che ha per assi le rette perpendicolari a due lati opposti
passanti per il loro punto medio.
 il rombo, che ha come assi le rette delle diagonali.
 il quadrato, che ha come assi quelli del rombo e quelli del rettangolo.
6
Parallelogrammi e trapezi
Definizione e proprietà del trapezio
Un trapezio è un quadrilatero che ha due lati paralleli.
Classificazione dei trapezi in base ai lati obliqui:
• se i lati obliqui sono diseguali il trapezio si dice scaleno.
• se i lati obliqui sono congruenti il trapezio si dice isoscele.
• se uno dei lati obliqui è perpendicolare alle basi il trapezio si dice rettangolo.
 In un trapezio gli angoli adiacenti a ciascuno dei lati obliqui sono
supplementari.
BAD + ADC = π
e ABC + BCD = π
7
Parallelogrammi e trapezi
Proprietà del trapezio isoscele
In un trapezio isoscele:
 gli angoli adiacenti a ciascuna base sono congruenti.
 le diagonali sono congruenti.
 la retta che passa per i punti medi delle basi è asse di simmetria.
Per riconoscere se un trapezio è isoscele basta verificare che sia vera
una delle seguenti relazioni:
• i lati obliqui siano congruenti (definizione);
• gli angoli adiacenti a una base siano congruenti;
• le diagonali siano congruenti;
• la retta che passa per i punti medi delle basi sia asse di simmetria
8
Parallelogrammi e trapezi
Corrispondenza di Talete
Teorema della corrispondenza di Talete
Se un fascio di rette parallele interseca una trasversale r nei punti A, B, C, ….. e una trasversale s nei
punti A’, B’, C’, ….., fra i due insiemi di punti si stabilisce una corrispondenza biunivoca che si chiama
corrispondenza di Talete.
Teorema di Talete
In tale corrispondenza, a segmenti congruenti sulla prima
trasversale corrispondono segmenti congruenti sulla seconda
trasversale.
Se AB ≅ CD allora A’B’ ≅ C’D’
9
Parallelogrammi e trapezi
Corrispondenza di Talete
Conseguenze del teorema di Talete nel caso dei triangoli
Se per il punto medio di un lato di un triangolo si traccia la parallela
ad un altro lato, questa taglia il terzo lato nel suo punto medio.
Il segmento che unisce i punti medi di due lati è parallelo al terzo
lato e congruente alla sua metà.
10