dinamica e strada - Liceo Daniele Crespi

Curvare in su, curvare in giù
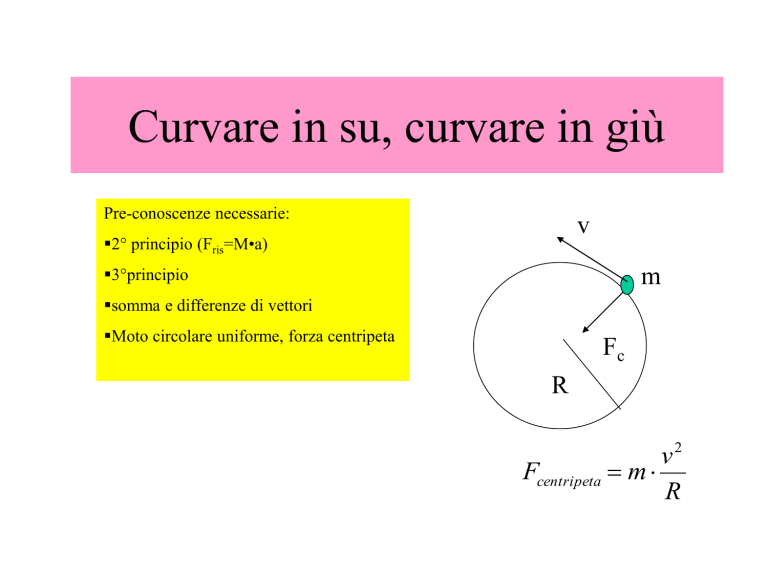
Pre-conoscenze necessarie:
v
2° principio (Fris=M•a)
3°principio
m
somma e differenze di vettori
Moto circolare uniforme, forza centripeta
Fc
R
v2
Fcentripeta  m 
R
Se ci si muove in piano, verticalmente la velocità è nulla e
tanto meno si accelera, la risultante delle forze è nulla
Rv
F=ksP
v
P=mg
Fris=P- Rv=0!!!
La “sensazione di peso” è data da Rv non da P !!
In questo caso è esattamente uguale a quella di quando siamo fermi, in piedi o seduti.
Non avvertiamo nulla di strano. Se la nostra massa è di 60 kg , “sentiamo” (sulle piante
dei piedi se siamo eretti, o …., se siamo seduti) una forza pari al nostro peso di 60 kgf
(circa 600 N)
Rv=Pn
F= Pt+ksPn
Pt=Psena
Pn=Pcosa
a
P=mg
Anche in questo caso la risultante delle forze è 0
La forza F necessaria a mantenere in moto la vettura è
aumentata della quantità Psena
Curvare in su.
(si può anche volare ….)
Rv
v
F= P-Rv
P=mg
Fris  ma
v2
P  Rv  m 
R
v2
Rv  mg  m 
R
Rv diminuisce !!!
R
(si “pesa” meno)
Quando Rv =0 si perde il contatto col suolo….e …si vola!!!
Ciò avviene quando
v2
g
R
cioè se : v  g  R
Ad esempio se R=90 m ciò avviene a v=30 m/s=108 km/h
Curvare in giù.
(si possono….rompere le sospensioni ….)
R
Rv
F= Rv - P
P=mg
Ci si sente schiacciare contro il
suolo, tanto più quanto più v è
elevata e R piccolo.
v2
Se
g
R
Fris  ma
v2
Rv  P  m 
R
v2
Rv  mg  m 
R
Rv aumenta !!!
(si “pesa” di più)
cioè se : v  g  R allora si " pesa" il doppio!
e…per finire con gli effetti speciali:
….il ‘giro della morte’
vlim
Rv=0
P=mg
R
Si può fare, se la velocità è
maggiore della velocità
limite vlim
Questa corrisponde alla
situazione in cui non c’è
contatto con la pista e
l’unica forza agente è il
Peso.
La massa non c’entra!!
Fris  ma
2
v
P  m  lim
R
2
v lim
mg  m 
R
v lim  R  g
Ad esempio per un
cerchio di raggio
R=12 m basta
arrivare su con v= 11
m/s (40 km/h)
Gli urti – La quantità di moto
Una conseguenza del 3° Principio della dinamica
se non agiscono altre forze sui due corpi
A e B, per il 2° principio della dinamica:
F BA
A
MA
Sono uguali
e
opposte
F AB
B
MB
FA B   FB  A
M B  aB   M A  a A
MB 
v B
v
 M A  A
t
t
ma, poiché la durata dell’interazione è
ovviamente la stessa per entrambi i corpi,
prima
dopo
prima
M B  ( v dopo

v
)


M

(
v

v
)
B
B
A
A
A
M A v dopo
 M B v dopo
 M A v Aprima  M B v Bprima
A
B
C’è dunque una quantità che resta costante, inalterata, durante un’interazione fra corpi
ed è la somma dei prodotti massa·velocità dei singoli corpi che compongono il sistema
di corpi.
Tale quantità si dice Quantità di moto, è ovviamente una grandezza vettoriale e, nel S.I.
si misura in kg·m/s
Quantità di moto:
p  mv
(kg  m/s)
Alcuni valori, tanto per farsi un’idea:
Una pallottola: m=20 g, v=400 m/s…….p=8 kg·m/s
Un’auto a 36 km/h
p= 10000
Un TIR a 80 km/h
p= 400000 kg·m/s
……………………
kg·m/s
Una diversa formulazione del 2° Principio della Dinamica
(Impulso e variazione della quantità di moto)
Fris  m  a
Fris  m 
v
t

Fris t  m  v  m  v dopo  v prima
Fris t  pdopo  p prima
Fris t  p
  p

Il prodotto forza agente per il
tempo durante il quale agisce
(Impulso) è uguale alla variazione
della quantità di moto del corpo.
A parità di variazione di p , …
tempi piccoli - forze grandi
tempi grandi - forze piccole
p prima  m  v
pdopo  0
p   m  v
F  t   m  v
Un calcolo realistico:
m=1000 kg v = 108 km/h = 30 m/s
F  t  30000 kg  m / s
v media(durante l'urto)  15 m / s
spaziopercorso durante l'urto  1 m
1
durata dell' urto t 
s
15
p  30000
F

 450000 N (45000 kgf )
t
1 / 15
E la testa del
guidatore?!
I danni al passeggero e al guidatore dipendono tutti dalla durata
dell’impatto:
Se la durata fosse quella dell’esempio precedente un corpo di
massa 5 kg subirebbe una forza di ben 2500 N ( 250 kgf) !!!
Ma se l’impatto è ammortizzato (cinture di sicurezza,
airbag) la durata dell’urto può divenire anche 10 volte più
grande e la forza agente proporzionalmente più piccola
Proprio come quando ci si butta dal terzo
piano e c’è il telo dei pompieri ad accoglierci
Quando la quantità di moto si conserva :
urti fra due corpi (in una dimensione)
Che cosa accade alla pistola quando spara ?
ptot  0
Dopo lo sparo, i due corpi
viaggiano in direzioni diverse ,
con velocità inversamente
proporzionali alle masse
Prima dello sparo, è un unico
corpo , fermo!
p proiettile  p pistola  0
m pr  v pr  M pisV pis  0
V pis  
m pr
M pis
 v pr
Ad esempio, se m=20 g , M= 800 g , v=400 m/s allora
V= -10 m/s
In uno scontro frontale tra due autoveicoli, avviene più
o meno la stessa cosa , anche se si svolge in senso
contrario !
I calcoli fondati sul principio di conservazione della
quantità di moto descrivono abbastanza accuratamente la
realtà, perché le forze esterne ( attrito col suolo soprattutto)
divengono, nella fase dell’urto, decisamente trascurabili.
L’urto, in questo caso è di tipo sostanzialmente
anelastico
in cui la gran parte dell’energia cinetica dei due veicoli va
persa e si trasforma in energia di deformazione e termica.
VC=80 km/h
VA=-40 km/h
prima
MC=4 t
mA=1 t
dopo
?
MC+A=5 t
prima
dopo
p tot
 p tot
M C  v C  M A  v A  M C  A  v C A
4  80 - 1  40  5  v C  A
v C A 
280
 56km / h
5
E, per finire, un bel tamponamento
prima
VA=80 km/h
mA=1 t
VC=40 km/h
MC=4 t
dopo
?
MC+A=5 t
Con che velocità prosegue l’ammasso di rottami?
Quale dei due autisti si fa più male, e perché?