CORSO DI FISICA
Prof. Francesco Zampieri
http://digilander.libero.it/fedrojp/
[email protected]
CORRENTI ELETTRICHE
LE CORRENTI
ELETTRICHE
MOTO DI CARICHE
Nel definire il potenziale abbiamo supposto di muovere le cariche dall’infinito
Quale condizione per il moto?
Deve esserci una FORZA MOTRICE =
Creazione di E in
una regione dello
spazio
E
Creazione di una
ddp V tra i punti
dello spazio
Come creo questo collegamento?
LA PILA DI VOLTA
A. Volta (1800)
Disco di Cu
Panno imbevuto di acido
Disco di Zn
I diversi metalli creano una DIVERSA CONCENTRAZIONE
DELLE CARICHE
Possibilità di creare una DDP che DEVE essere
associata ad un CAMPO EL.
–
+
Rame: maggior concentrazione di
elettroni (regione ove prevalgono
cariche
negative
=
POLO
NEGATIVO
Zinco: minor concentrazione di
elettroni (regione ove prevalgono
cariche
positive
=
POLO
POSITIVO
In un acido la concentrazione delle cariche può agevolare il
passaggio di elettroni
L’effetto è amplificato se uso più celle sovrapposte
GENERATORE DI TENSIONE (ddp)
generatore
CIRCUITO
ELETTRICO
utilizzatore
Se collego un GENERATORE DI TENSIONE ad un
conduttore e ad un UTILIZZATORE ho vari effetti
Se l’utilizzatore è una lampadina,
si accende!
SPIEGARE
QUESTI
FENOMENI!
ELETTRODINAMICA studia il moto delle cariche soggette
a E, ovvero a ddp
E
q
F subita = q·E
Il moto avviene nella direzione del campo elettrico E (il verso
dipende dal segno!)
Se E è uniforme, la carica subisce MOTO UNIF. ACCEL (perché
soggetta a F costante)
MOTO DI CARICHE IN UN CONDUTTORE
Un conduttore metallico sottoposto a E
Sezione di
conduttore
E
v
Gli elettroni di conduzione vengono sospinti dal campo elettrico
creato dalla ddp ai capi.
Si crea un “fiume” di cariche negative che si muovono
CONTRARIAMENTE AL CAMPO ELETTRICO!
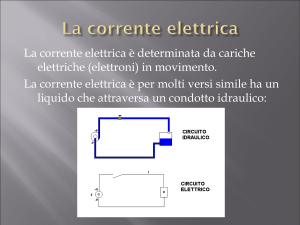
IL FIUME DI CARICHE
Lo spostamento delle cariche è analogo ad una corrente
idraulica
PORTATA DI UN FIUME = m3
di acqua che in 1s fluiscono
attraverso la SEZIONE S del
fiume
Quale la portata del fiume di cariche?
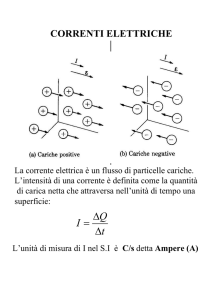
LA CORRENTE ELETTRICA
q
“PORTATA” = quantità di carica che in 1s passa attraverso la
sezione del conduttore
q
I
t
[I] = C/s = AMPERE (A)
1 A è la corrente che si genera quando 1C di carica fluisce in 1s attraverso la
sezione del conduttore
Verso di I
Circuito
elettrico
+ –
V
Se ho una ddp V ai capi, essa mi farà fluire una certa corrente
attraverso la sezione del conduttore
C.El.: da + a –, ma le cariche si spostano da – a +.
Per convenzione, il verso della corrente si assume SEMPRE
COME IL CAMPO ELETTRICO
LE LEGGI DI OHM
ci dicono le MODALITA’ con cui la corrente fluisce in un
circuito
LA PRIMA LEGGE
Ci dice come la ddp V ai capi influenza la corrente I che fluisce
nel circuito
Se aumento V, come varia I?
C’è da pensare che una ddp maggiore è associata ad un E
maggiore, quindi le cariche si muovono più velocemente
I aumenta
Ma quale legge? Quale dipendenza?
Per alcuni conduttori la dipendenza tra I e V è LINEARE
I misurata
Rapporto costante
I/V = K
V variabile (es. variando il
I K V
numero delle pile inserite)
Che significato ha la costante K?
K è la costante di proporzionalità = PENDENZA DELLA RETTA
Aumento maggiore
I
CONDUTTORE 2
Aumento minore
CONDUTTORE 1
V
Tanto minore è l’aumento, quanto meno facilmente avviene la
conduzione di I C’E’ MAGGIORE… RESISTENZA!!
Tanto maggiore è l’aumento, quanto più facilmente avviene la
conduzione di I C’E’ MINORE… RESISTENZA!!
LA RESISTENZA ELETTRICA
Definisco una nuova grandezza detta
RESISTENZA R del conduttore, tale che:
1
K
R
R misura la DIFFICOLTA’ da parte del conduttore a far
passare I
LA PRIMA LEGGE DI OHM
Se I = K·V = 1/R ·V
V = R·I
In questa maniera, [R] = Volt / Ampere = OHM
Non tutti i conduttori la seguono, solo quelli OHMICI
INTERPRETAZIONE MICROSCOPICA DI R
Microsc. una carica è ostacolata nel suo moto entro conduttore
1) Dalle altre cariche
2) Dai protoni dei nuclei
URTI dei portatori
di corrente contro il
reticolo cristallino
del conduttore
DA COSA DIPENDE TALE DIFFICOLTA’?
E’ misurata da R
1) Caratt.fisiche del conduttore (tipo e disposizione dei
legami, dislocazione dei nuclei)
l
2) Lunghezza del conduttore (l , R )
3) Sezione S del conduttore (S , R)
SECONDA LEGGE DI OHM
l
R
S
= RESISTIVITA’del materiale (rende conto della dip. di
R dal materiale e dalla sua T)
dipende da T
Dipendenza di da T
Se T è alta, il materiale ha particelle con grande agitazione
termica più difficile moto cariche all’interno e quindi
deve aumentare
= 0(1+T)
difficoltà nel moto CAUSATA DA URTI fra le cariche e le
particelle del materiale
URTO = DISSIPAZIONE DI ENERGIA (cfr. attrito!)
Ecin_1 < Ecin_0
Ecin_0
prima
Sezione
cond.
dopo
COSA IMPLICANO LE PERDITE DI ENERGIA?
Necessità
di
ripristinare
continuamente ddp (un generatore SI
SCARICA!)
DISSIPAZIONI
(U < 0)
EFFETTI TERMICI
(macroscopici) dovuti a URTI
(microscopici)
EFFETTO JOULE DELLA CORRENTE
L’energia dissipata dalle cariche a causa degli urti, viene data alle
particelle del conduttore
La carica perde
energia
Sezione cond.
Le partic. del mezzo sono state
urtate e hanno RICEVUTO
ENERGIA
Le partic. del conduttore hanno
incrementando U interna e quindi T
ricevuto
energia,
EFFETTO JOULE = effetto di riscaldamento di
un conduttore percorso da corrente
Macrosc. è dato dagli urti microscopici tra cariche in moto e
partic. del conduttore
Un conduttore attraversato da corrente subisce un incremento
di T proporzionale alla sua resistenza R
Funzionamento di phon, stufe elettriche…
Per effetto Joule, alcuni conduttori, scaldandosi,
EMETTONO ANCHE RADIAZIONE VISIBILE
Es. lampadina!
Come MISURARE le dissipazioni?
Calcolo il LAVORO DISSIPATO nell’attraversamento di
un conduttore di resistenza R dalla corrente I
L = q·V
L q V
P
t
t
Se ora divido per t, ho POTENZA
Ma q/t = I
P I V
P = V·I
Se ora vale la prima legge di Ohm:
V = R·I
P R I
2
E’ la potenza dissipata attraversando la resistenza R
Se poi conosco il tempo di attraversamento t, si ha:
L = P·t =
2
RI
t
Es. 1KWh = 3.600.000 J di energia elettrica in 1h di
utilizzazione!
Conoscendo la potenza in kW di un elettrodomestico,
se conosco il tempo di utilizzo, posso risalire al
consumo in energia!
I CIRCUITI ELETTRICI
Si dice CIRCUITO ELETTRICO un insieme di:
•Corpi conduttori (fili)
•Generatori di tensione (pile, ecc..)
•Utilizzatori (lampadine)
•Elementi quali: condensatori, induttanze, ecc..
+ STRUMENTI DI LETTURA (Amperometri, Voltmetri)
LA RESISTENZA COME ELEMENTO DI
UN CIRCUITO
Ogni conduttore ha una RESISTENZA R che si può
immaginare CONCENTRATA in un punto qualsivoglia del
circuito
I
R
V
IL CIRCUITO OHMICO
R
V
Se vale la legge di Ohm, per la R attraversata, c’è una
CADUTA DI TENSIONE AI CAPI
V = R·I
I è la corrente che attraversa
la resistenza
IL COLLEGAMENTO DELLE RESISTENZE
Allo scopo di CREARE DELLE CADUTE DI
TENSIONE (es. lampadine che sopportano al max una certa Imax),
si possono inserire altre resistenze in due modi:
IN SERIE ( una dopo l’altra) saranno attraversate
dalla stessa I
R
IN PARALLELO causeranno la stessa caduta
di tensione, ma sono attraversate da correnti
diverse
RESISTENZE IN SERIE
R2
R1
I
R1 e R2 sono attraversate dalla stessa corrente I
VTOT = V1 + V2
Posso pensare di sostituire le due resistenze con
UN’UNICA RESISTENZA
DETTA EQUIVALENTE Req
Come dipende Req da R1 e R2?
Req è tale che V TOT = I·R eq
Ma se il salto di potenziale è la somma dei due salti dovuti a
R1 e R2:
V TOT = R1 · I + R2 · I = I ·(R1 + R2)
ALLORA
Req = R1 + R2
N
Se ho N resistenze, allora:
Req Ri
i 1
Req
è
sempre
maggiore
delle
singole R!
RESISTENZE IN PARALLELO
R1
I1
I2
R2
Ai capi c’è sempre la stessa ddp!
V
Posso pensare di sostituire le due resistenze con
UN’UNICA RESISTENZA
DETTA EQUIVALENTE Req
Come dipende Req da R1 e R2?
V
I
Ovviamente Req sarà tale che: V TOT = I·Req
Req
V
V
I2
Ma I = I1+I2
I1
R2
R1
V V
V
I
R1
R2
Req
1
1
1
Req R1 R2
Req è sempre
MINORE della
più piccola
IL CONDENSATORE
Sistema formato da due conduttori (piastre o armature) su
cui si deposita carica Q UGUALE MA DI SEGNO
OPPOSTO (caricate x induzione)
Es. condensatore piano
+
Q
+
+
+
+
+
Si instaura un c.el. UNIFORME
E
–
–
–
–
–
–
–
Un condensatore serve per ACCUMULARE LE CARICHE in un
circuito
Se accumulo una certa quantità di carica, creo un c.el. e quindi
una certa ddp fra le armature
Si dim. che
Q/V = cost = C
CAPACITA’ DEL
CONDENSATORE
C dipende solo dalle caratteristiche geometriche del
condensatore e dal mezzo interposto
[C]= C/V = FARAD
F
IL CONDENSATORE come elemento di un circuito
(il circuito RC)
R
C
V
Anche i condensatori possono essere collegati IN SERIE O IN
PARALLELO!
CONDENSATORI IN SERIE
C1
C2
La carica che si deposita sulle armature è la stessa e vale Q
Il salto totale di potenziale vale V TOT = V1 + V2
Si può immaginare di sostituire i due
condensatori con un unico Ceq
Come dipende la capacità di Ceq da C1 e C2?
Ceq è tale che:
VTOT
Q
Q Q
V1 V2
Ceq
C1 C2
1
1
1
Ceq C1 C2
CONDENSATORI IN PARALLELO
Subiscono lo stesso salto
di potenziale V
C1
C2
La carica che si deposita sulle armature è
diversa: Q1 e Q2, con Qtot = Q1+Q2
Si può immaginare di sostituire i due
condensatori con un unico Ceq
Come dipende la capacità di Ceq da C1 e C2?
Ceq è tale che
QTOT
V
QTOT Ceq V
Ceq
Q1= V ·C1 e Q2= V ·C2
Q= Q1+Q2= V ·C1 + V ·C2= V ·(C1+C2)
Ceq = C1+C2