Tale algoritmo si può trasformare facilmente in un algoritmo che testi

Teoria dei numeri
Lezione del giorno 18 maggio 2009
Algoritmo di fattorizzazione  di Pollard.
Premettiamo alcune considerazioni su un argomento di Calcolo delle Probabilità.
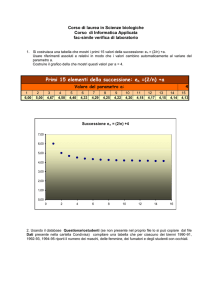
Siano n,m numeri naturali con 1<n<m, S un insieme finito di cardinalità m e sia data una
successione finita di n termini scelti in S (anche non distinti):
a1, a2, ……, an
in modo che gli ai siano scelti random in modo “uniforme” (dal punto di vista della probabilità) fra
gli elementi di S (nel senso che per ogni indice i, ogni elemento dell’insieme S ha la stessa
probabilità di essere scelto come elemento ai).
Calcoliamo la probabilità che almeno 2 degli elementi della successione coincidano.
Calcoliamo dapprima la probabilità che tutti gli elementi della successione siano distinti.
Fissato a1, la probabilità che a2 sia diverso da a1 è (m-1)/m; fissati a1,a2 distinti, la probabilità che a3
sia diverso da a1 e da a2 è (m-2)/m , quindi la probabilità che a1, a2, a3 siano tutti distinti è il
prodotto [(m-1)/m][(m-2)/m]=(1-1/m)(1-2/m)
Iterando il ragionamento si ottiene che la probabilità che a1, a2, ….., an siano tutti distinti è il
prodotto:
(1-1/m)(1-2/m)……(1-(n-1)/m).
Dallo sviluppo in serie ex=1+x+x2/2!+…, possiamo approssimare 1+x con la funzione ex, di modo
che ogni fattore del prodotto precedente è approssimato (ponendo x= -i/m con i=1,….,n-1) dalla

n ( n -1)
2m
funzione e-i/m. Dunque il prodotto è approssimato dalla funzione e
(tenendo conto che la
soma 1+2+….+(n-1) coincide con n(n-1)/2): per n “grande” possiamo approssimare n(n-1) con n2,
di modo che la probabilità che tutti gli elementi della successione siano distinti è approssimata dalla

n2
2m e dunque la probabilità che almeno 2 degli elementi a1, a2, ….., an coincidano è
funzione e
(con approssimazione) la seguente funzione di n,m:
p(n,m)  1  e

n2
2m
Se allora fissiamo un valore di probabilità p con 0<p<1, il numero n degli elementi di una
successione per i quali sia p la probabilità che fra essi almeno 2 coincidano è approssimativamente:
1
)]
n  2m[log e (
1 p
In particolare per esempio se fissiamo una probabilità del 50% (p=0.5), si ottiene n  1,77 m ,
mentre se se fissiamo una probabilità del 90% (p=0.9), si ottiene n  2,14 m .
Dunque se scegliamo in successione in modo “random” elementi dell’insieme S:
a1, a2, a3, ………………..
il minimo indice n per cui l’elemento an coincide con almeno uno degli elementi che lo precedono è,
dal punto di vista probabilistico, di ordine O( m ).
Un’applicazione di tale teoria é appunto il cosiddetto “paradosso dei compleanni”: se sono scelte
random un numero n di persone con 1<n<365, la probabilità che almeno 2 fra esse compiano gli
anni nello stesso giorno e mese dell’anno è  1  e

n2
730
; inoltre, fissato un valore di probabilità p
con 0<p<1, il numero n di persone (scelte random) per le quali la probabilità che fra esse almeno 2
1
)]
compiano gli anni nello stesso giorno e mese dell’anno è  730[log e (
1 p
(tutto questo supponendo che giorno e mese di nascita degli esseri umani siano distribuiti in modo
uniforme fra i 365 giorni dell’anno, il che non è vero in pratica).
Per esempio se la probabilità fissata è del 50% (p=0,5), n  730[log e 2 ]  23: scegliendo 23
persone in modo random, la probabilità che fra esse almeno 2 compiano gli anni nello stesso giorno
e mese dell’anno è  50% (abbastanza paradossale…..).
Scegliendo invece 50 persone in modo random, la probabilità che almeno 2 fra esse compiano gli
anni nello stesso giorno e mese dell’anno è addirittura  97%.
Introduciamo ora l’ Algoritmo di fattorizzazione  di Pollard.
Tale algoritmo (1975) ha avuto il suo più grande successo nel 1980, quando ha permesso di
8
calcolare la fattorizzazione del numero di Fermat F8= 2(2 ) +1 (di cui con il test di Pepin si era già
dimostrata la non primalità), trovando un fattore (primo) di 16 cifre, con un cofattore di 62 cifre
(che nel 1981 è stato dimostrato primo anch’esso).
Il metodo  di Pollard si basa sulle seguenti considerazioni.
Supponiamo di volere fattorizzare un numero intero n>1, cercando un divisore non banale di n (se
esiste, cioè se n non è primo).
Sappiamo che n ha certamente un divisore primo p n , e formalmente (pur non conoscendo p a
priori) consideriamo gli insiemi:
S={0,1,2,…,p-1}
T={0,1,2,…,n-1}S
Sia poi F: T  T una funzione che soddisfa: F(xmodp)=F(x)modp per ogni xT.
Fissato un elemento sT (seme), costruiamo una successione ak di elementi di T (con k=0,1,2,….)
ponendo induttivamente:
a0=s; ak=F(ak-1) per ogni k>0
(in pratica a partire dal seme s, si applica successivamente più volte F per ottenere i termini
seguenti)
In corrispondenza (utilizzando le riduzioni modulo p) possiamo costruire una successione bk di
elementi di S ponendo bk=akmodp .
Ora supponiamo che gli elementi di S siano distribuiti in modo uniforme (dal punto di vista
probabilistico) nella successione bk (cioè che per ogni k la probabilità che un elemento di S coincida
con bk sia uguale per tutti gli elementi).
Per le considerazioni svolte in precedenza (paradosso dei compleanni), il minimo indice k per cui b k
coincide con uno dei termini che lo precedono (bj=bk con j<k) è dal punto di vista probabilistico di
ordine O(S2)=O(p2).
Se bj=bk con j<k, allora bj+1=bk+1 (perché bj+1=aj+1modp=F(aj)modp=F(ajmodp)=F(bj)= F(bk)=bj+1);
analogamente si ha bj+2=bk+2 e in generale (per induzione):
bj+m=bk+m
per ogni m0 (*)
Se fissiamo un qualunque indice ij si ha allora, applicando la (*) con m=i-j):
bi=bj+(i-j)=bk+(i-j)=bi+(k-j)
Analogamente si ha bi= bi+2(k-j) e in generale (per induzione):
bi =bi+t(k-j)
per ogni t0 (fissato l’indice ij)
Poiché i+t(k-j) rappresenta il generico indice ri che sia congruo i modulo (k-j) otteniamo il
seguente risultato:
comunque presi due indici i,rj, se ir (mod k-j) allora bi=br .
In pratica la successione bi diventa ciclica con “periodo” k-j, nel senso che dal termine di indice j in
poi i termini coincidono ogni k-j posizioni.
Per esempio se j=3, k=9, la successione diventa ciclica con periodo 6 dal termine di indice 3 in poi:
infatti dall’indice j=3 in poi, due qualunque termini della successione, i cui indici differiscano per
un multiplo di k-j=6 (cioè i cui indici siano congrui modulo 6), coincidono fra loro.
Rappresentando graficamente la situazione, si ottiene (per j=3, k=9):
b5=b11=b17=….
b4=b10=b16=….
b6=b12=b18=….
b7=b13=b19=….
b3
b2
b8=b14=b20=….
b1
b0
Notare la forma geometrica che richiama la struttura della lettera greca  (da cui il nome
dell’algoritmo).