Document

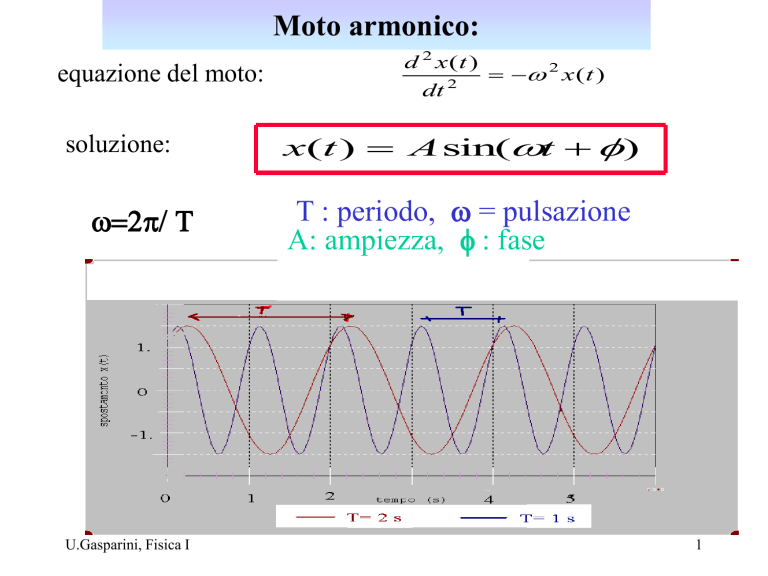
Moto armonico:
equazione del moto:
soluzione:
2p/ T
U.Gasparini, Fisica I
d 2 x (t )
dt 2
  2 x ( t )
x(t )  A sin(t   )
T : periodo,  = pulsazione
A: ampiezza,  : fase
1
spostamento:
x (t )  X 0 sin(t )
velocità:
dx (t )

dt
 X 0 cos(t )
v (t ) 
accelerazione:
dv (t )

dt
  X 0 2 sin(t ) 
a (t ) 
  2 x (t )
U.Gasparini, Fisica I
2
Esempi di moto armonico:
i) moto di un punto materiale di massa m sotto l’azione di una “forza elastica”:
F = -k x ux
F
x < 0.
Fx = -k x > 0.
x
x (posizione di equilibrio)
x > 0.
Fx = -k x < 0.
F
x
x
Legge di Newton: F = m a
 kx ( t )  m
U.Gasparini, Fisica I
con:
Fx = m a x
d 2 x (t )
dt
2
   k/m
d 2 x (t )
dt 2
  2 x ( t )
3
“Pendolo semplice”
In un piano verticale sotto l’azione della forza peso mg , per piccole oscillazioni
intornoalla posizione di equilibrio (asse verticale):
ma = Ftot = mg + t
l
t
m
q
Proiezione sull’asse tangente T:
maT = mg sin q
a
m
q
mg
l
dq
ds
dt
T
Vale la relazione geometrica: ds = - l dq
d s(t )
d  (t )



dt 2
dt 2
2
d 2 s( t )
2
 mg sin q ( t )
Pertanto:
 ml
d 2q ( t )
dt
2
 mg sin q ( t )
Per piccole oscillazioni: sinq q
d 2q ( t )
dt 2
U.Gasparini, Fisica I
2
  2q ( t )
con:
 g/l
4
Legge oraria del moto del pendolo :
Moto di un pendolo semplice per piccole oscillazioni:
d 2q ( t )
dt 2
Legge oraria:
q (t )  q0 sin(t   )
T 
Periodo:
  2q ( t )
2p

 2p

g
indipendente dalla massa m del pendolo:
“isocronismo” del moto;
dalla misura di T  determinazione di g
U.Gasparini, Fisica I
5
Energia in un moto armonico
x(t )  X 0 sin(t   )
spostamento:
velocità:
v (t ) 
dx (t )
 X 0 cos(t   )
dt
Energia cinetica:
E k (t ) 
1
1
2
mv 2 
mX 02 2  cos(t   )
2
2
Energia potenziale:
x
E p (t )  

0
F ( x ' )dx ' 

1
1
kx 2 
kX 02 sin(t   )
2
2
E(t)
U.Gasparini, Fisica I
t
6

2
Energia meccanica:
E M  Ek  E p 



1
1
2
2
2

mX 0  cos(t   )  kX 02 sin(t   )
2
2
1
1
2
2
2

kX 0 cos (t   )  sin (t   ) 
kX 02
2
2
k
2 
m


Ek  E M  E p
2
EM= k X0 /2 = costante
Ep

2
E(x)
 EM 
1
kx 2
2
1
 kx 2
2
U.Gasparini, Fisica I
-X0
x
0.
X0
7