Document

Forza gravitazionale di un corpo sferico omogeneo
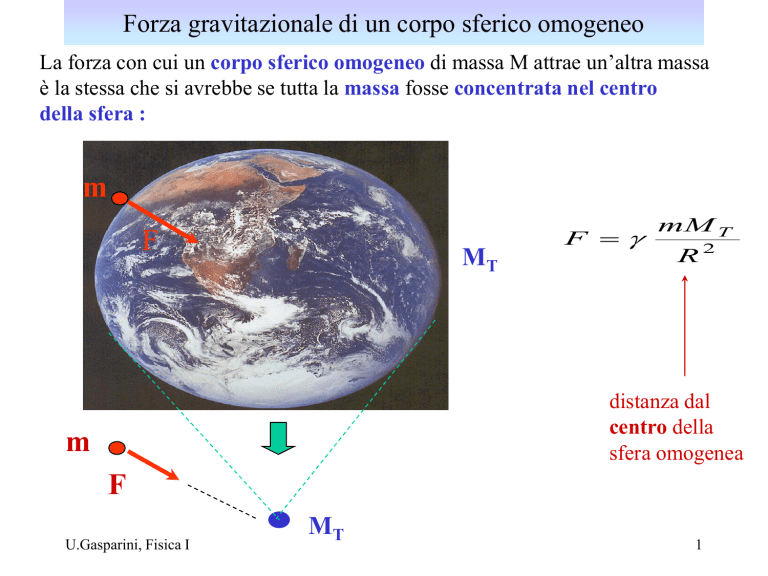
La forza con cui un corpo sferico omogeneo di massa M attrae un’altra massa
è la stessa che si avrebbe se tutta la massa fosse concentrata nel centro
della sfera :
m
F
MT
F  
mM T
R2
distanza dal
centro della
sfera omogenea
m
F
U.Gasparini, Fisica I
MT
1
“Guscio sferico”
Forza esercitata sulla massa mP da un
“guscio sferico” di massa M:
C
 dF
distanza da mP a dm
dm
dr
r
F 
forza esercitata
dall’ “anello” di massa dM
x
Ra

forza esercitata
da dm su mP
df =  mPdm / x2
a
dF
P
x cosa  R  r cos
d
mP
R
“anello” di raggio Ra=r sinq
e massa dM = dV   2Ra rddr   2r sin rddr   2r 2 sin ddr
dV
dF 

cos adf  cos a  
anello

mP dm
mP


cos a  dm
2
2
x
x
mP
mP
2
cos
a
dM


cos
a
2

r
sin ddr
x2
x2
U.Gasparini, Fisica I
R  r cos
x
(vedi
seguito)
dM
dM
xdx
Rr
2
x
r
x 2  ( R  r cos  ) 2  r 2 sin 2 

 R 2  2 Rr cos  r 2
Differenziando:
R
2 xdx  2 Rr sin d
Quindi:
dF  ( R  r cos  )
mP
x2
 2r
 r cos
dx
dr
R
sin d 
xdx
Rr
x 2  R2  r 2

2R
 R2  r 2

mP

dF  

1

rdxdr
x2
R2


Forza esercitata dall’intero ‘guscio’ di massa M :
 dF
F 

guscio
F 
mP
R
2
mP
R2
 4r dr  
U.Gasparini, Fisica I
2
M
R r
 R2  r 2


rdr
 1 dx
2
x


R r

mP
R
2
M
massa del guscio sferico
4r
3
Campo della forza gravitazionale
Forza gravitazionale esecitata da una massa M su una massa m:
F ( r ) = -  M m uR
r2
r
M
m
uR
F
“Campo gravitazionale” generato dalla massa M:
G(r)
U.Gasparini, Fisica I
P
G( r )  F( r ) = -  M uR
m
r2
“linee di forza” del campo:
tangenti in ogni punto alla
direzione del campo
4
Campo gravitazionale generato da due masse uguali:
P1
G
P2
Le linee di forza “visualizzano” l’andamento del campo; la loro densità è
proporzionale all’intensità del campo.
U.Gasparini, Fisica I
5
“Flusso” di un campo vettoriale
“Flusso” del campo vettoriale G attraverso una
superficie orientata infinitesima :
G


d  G  dS
dS= dS uN
superficie di area dS
Flusso attraverso una superficie finita S:
G
S 
U.Gasparini, Fisica I
dS
 d
S


S


G  dS
6
Teorema di Gauss :
Il flusso del campo gravitazionale attraverso una qualsiasi superficie chiusa
è proporzionale alla somma delle masse all’interno della superficie:
S 



G  dS  4
m
i
i
S
G
S
mi
Mj
In particolare:
S 

S


G  dS  G ( r )4r 2  4m
S
r
teorema di Gauss
G(r ) 
U.Gasparini, Fisica I
m
r
2
G=-G(r )u R
m
7
Applicazione del teorema di Gauss :
Forza gravitazionale all’interno di una sfera omogenea di massa M :
G= - G( r) uR
r
m(r)
S 
R
G (r ) 
m( r )
r2



G  dS  G ( r ) 4r 2  4m( r )
S


4
r 3 
3
r2
G(r ) 
4
r
3
Forza gravitazionale su una massa m a distanza r dal centro di una distribuzione
sferica di raggio R e massa :
F (r ) 
mG ( r )

M 
4
rm
3
mM
r<R
U.Gasparini, Fisica I
4
R 3
3
r2
R
r>R
r
8
Energia potenziale della forza gravitazionale
U 12


 U ( r2 )  U ( r1 )  W1 2  
2

 

F ( r )  ds
1

r1
M
m
1
F
mM 
uR
r2
ds

r2
2



uR  ds  uR ds cos  dr
2
U 12  mM



u R  ds
1
r2
r2
 mM
1
U ( r2 )  U ( r1 )  mM
r
Posto :

r1  
U.Gasparini, Fisica I
r2
r1
uR
r
dr
2
ds
r1
 1
1


 mM

r
r
 1
2 
U (r1  )  0
U ( r )  
r2  r
mM
r
9
“Velocità di fuga”
E’ la minima velocità iniziale v0 (nel punto a distanza r = R) necessaria per sfuggire
all’attrazione gravitazionale ( per arrivare ad r =  con velocità nulla)
U(r)
R

mM
R
Dalla conservazione
dell’ energia meccanica:
r

mM
r
i
U ( R)  E k
 U (r  )  E kf

mM
1
2

mv0
 0
R
2
v0 
Per la Terra:
R  RT  6.4  106 m
2M
R
M T  6.1024 kg
v0  11km / s
Per il Sole:
U.Gasparini, Fisica I
R  RS  10 2 RT  0.7 10 6 km
M S  106 MT  1030 kg
10 / s
v0  620km
Il viaggio del “Voyager”
Nella sua traiettoria, ha utilizzato i pianeti giganti come
“fionde gravitazionali”, per raggiungere
i pianeti esterni del sistema solare
Giove (Feb.1979)
Terra (Sett.1977)
Saturno (Ott.1980)
Urano (Gen.1986), Nettuno (Ago.1989)
Ha inviato i suoi ultimi segnali qualche hanno fa, dopo aver superato l’ orbita di Plutone;
attualmente vaga nello spazio interstellare, a circa 10 miliardi di km da noi; è l’oggetto più lontano
mai lanciato dall’ Uomo. Potrebbe raggiungere Proxima Centauri, la stella più vicina al Sole (4,2 anni-luce),
tra circa 40000 anni.
U.Gasparini, Fisica I
11
“Curva di rotazione”
“Curva di rotazione”(o cuva“kepleriana”) del sistema solare:
dalla legge di gravitazione universale, per un pianeta in orbita circolare di raggio R:
v2
mM
ma  m

R
R2
v(km/s)
40.
v 
M
R
Venere
Terra
30.
Marte
20.
Giove
Saturno
10.
Urano
0.5
1.
1.5
2.
2.5
3.
R (10 9 km)
La curva di rotazione della nostra galassia
(“Via Lattea”) non segue la stessa legge:
1.
v(km/s)
200.
Ammassi
globulari
Sole
100.
Grandi nubi di
Magellano
Piccole nubi
di Magellano
U.Gasparini, Fisica I
50.
100.
150.
200.
R(103 ) anni-luce
12
Curva di rotazione delle galassie
La “curva di rotazione” delle galassie non segue la legge kepleriana :
per spiegare l’andamento di v(r) delle stelle nelle galassie, misurato dall’osservazione
del ‘redshift’ (= spostamento verso il rosso) degli spettri di emissione della luce, è
necessario ammettere l’esistenza di materia oscura nell’Universo
(es.: stelle di neutroni, buchi-neri, neutrini, nuove particelle di natura sub-nucleare…)
che contribuisca alla massa totale della galassia stessa, sorgente della forza
gravitazionale
U.Gasparini, Fisica I
13