Capitolo 3
La struttura
dell'atomo
Copyright © 2012 Zanichelli editore
3.1 La doppia natura della radiazione
elettromagnetica
3.2 Gli spettri atomici dimostrano che gli
elettroni possiedono energie quantizzate
3.3 Il modello atomico di Bohr interpreta lo
spettro dell’idrogeno
3.4 La crisi della meccanica classica porta al
modello atomico a orbitali, o quanto
ondulatorio
3.5 Lo spin dell’elettrone influenzala
distribuzione degli elettroni negli orbitali
3.6 Dove l’elettrone passa il suo tempo
Compact discs and DVDs are possible because information
recorded on them can be read by tiny light sources called
lasers. The laser emits highly monochromatic light (light of a
single color), which is reflected from the surface of the CD or
DVD, producing a
flickering beam containing the information that’s ultimately
translated into sound and/ or picture. The light from a laser is
produced by electrons undergoing energy changes
within atoms. Such energy changes are related to the
electronic structure of atoms,which is the principal topic of this
chapter.
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN’ONDA
L’energia coinvolta nelle reazioni chimiche è fondamentalmente
energia termica ma, in chimica, assume una notevole importanza
anche un altro tipo di energia: l’energia elettromagnetica,
comunemente detta energia luminosa. Questa forma di energia si
propaga nello spazio a una velocità straordinariamente elevata per
mezzo di onde elettromagnetiche che prendono origine da una
carica elettrica oscillante. Quanto più ampia è l’oscillazione della
carica, tanto maggiore è l’ampiezza dell’onda. L’ampiezza
determina l’intensità o luminosità della radiazione. ■ 3.1 illustra
Copyright © 2012 Zanichelli editore
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN’ONDA
Quanto più ampia è l’oscillazione della carica, tanto maggiore è
l’ampiezza dell’onda. L’ampiezza determina l’intensità o luminosità
della radiazione. Il numero di cicli compiuti in un secondo è detto
frequenza della radiazione elettromagnetica, rappresentata dal
simbolo ν (la lettera greca ni).
L’unità SI di frequenza si chiama hertz (Hz) (1 Hz 1 s-1).
La distanza tra due massimi (o due minimi) consecutivi prende il
nome di lunghezza d’onda della radiazione ed è rappresentata dal
simbolo λ (la lettera greca lambda).
c
Copyright © 2012 Zanichelli editore
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN’ONDA
Poiché la lunghezza d’onda è una distanza, questa viene espressa
con l’unità di lunghezza (il metro).
Moltiplicando la lunghezza d’onda per la frequenza, otteniamo la
velocità dell’onda.
La velocità della radiazione elettromagnetica nel vuoto è costante ed
è nota come velocità della luce. Approssimandone il valore a tre
cifre significative, questa corrisponde a 3,00 108 m/s (o m s-1); il
simbolo che rappresenta questa importante costante fisica è c:
c
Copyright © 2012 Zanichelli editore
Possiamo quindi descrivere una relazione di fondamentale importanza
che lega ν a λ . Questa relazione ci suggerisce che le due grandezze
sono inversamente proporzionali e che la costante di proporzionalità è
c, la velocità della luce.
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LO SPETTRO ELETTROMAGNETICO RAGGRUPPA E ORDINA
LE RADIAZIONI
La radiazione elettromagnetica comprende un ampio intervallo di
frequenze e di lunghezze d’onda, lo spettro elettromagnetico.
Ogni parte dello spettro ha un nome di uso comune.
c
Copyright © 2012 Zanichelli editore
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LO SPETTRO ELETTROMAGNETICO RAGGRUPPA E ORDINA
LE RADIAZIONI
L’occhio umano riesce a percepire solo una banda molto ristretta di
lunghezze d’onda, in un intervallo compreso fra circa 400 nm e circa
700 nm. Questa banda è lo spettro visibile e comprende tutti i
colori dell’iride, dal violetto al rosso. La luce bianca è un insieme di
tutti questi colori, combinati in quantità approssimativamente uguali.
Quando un fascio di luce bianca attraversa un prisma, le frequenze si
separano formando lo spettro visibile.
L’assorbimento della radiazione elettromagnetica è particolarmente
utile per il riconoscimento delle sostanze.
c
Copyright © 2012 Zanichelli editore
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN FASCIO DI FOTONI
Nel 1900, il fisico tedesco Max Planck (1858-1947) propose che la
radiazione elettromagnetica fosse costituita da fasci di minuscoli
«pacchetti» o quanti di energia, che più tardi vennero chiamati
fotoni. Ciascun fotone viaggia alla velocità della luce. Albert Einstein
(1879-1955) confermò successivamente il suggerimento di Planck:
l’energia di un fotone è proporzionale alla frequenza della
radiazione elettromagnetica e non alla sua intensità o luminosità
(legge di Planck), come si era creduto fino a quel momento:
c
Copyright © 2012 Zanichelli editore
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN FASCIO DI FOTONI
Copyright © 2012 Zanichelli editore
h è una costante di proporzionalità chiamata costante di Planck.
L’equazione due significati fisici estremamente importanti. Per prima
cosa essa ci dice che l’energia della radiazione non si trasferisce
mediante un flusso continuo ma sotto forma di «pacchetti» distinti.
Questo aspetto implica che l’emissione o l’assorbimento di tale
energia può essere possibile soltanto secondo multipli interi di quella
trasportata dal singolo fotone e non secondo sue frazioni. Inoltre, la
legge di Planck collega fra loro le due descrizioni della radiazione
elettromagnetica: la parte sinistra dell’equazione si riferisce a una
proprietà delle particelle (l’energia del fotone) mentre la destra
esprime una proprietà delle onde (la frequenza).
c
3.1 LA DOPPIA NATURA DELLA RADIAZIONE ELETTROMAGNETICA
►LA RADIAZIONE ELETTROMAGNETICA PUÒ ESSERE
DESCRITTA COME UN FASCIO DI FOTONI
Copyright © 2012 Zanichelli editore
La teoria dei quanti riunisce le due interpretazioni, consentendo di
utilizzare l’una o l’altra per descrivere i risultati sperimentali. La
scoperta di Planck ed Einstein fu veramente sorprendente. Per un
evento che richiede energia e dipende dall’assorbimento di luce,
come la fotosintesi delle piante verdi, è importante la frequenza della
luce e non la sua intensità. Ciò si spiega quando consideriamo la luce
come un fascio di fotoni: una «frequenza elevata» corrisponde a una
maggiore energia dei fotoni, mentre un’intensità più alta implica un
maggior numero di fotoni.
L’idea che la radiazione elettromagnetica possa essere
rappresentata, allo stesso tempo, come un fascio di fotoni e come
un’onda è il fondamento della teoria dei quanti (dualismo ondaparticella).
c
3.2 GLI SPETTRI ATOMICI DIMOSTRANO CHE GLI ELETTRONI
POSSIEDONO ENERGIE QUANTIZZATE
Lo spettro visibile, è chiamato spettro continuo perché contiene luce
di tutti i colori. Si forma quando la luce emessa dal Sole, o da qualsiasi
altro oggetto solido o liquido che sia stato riscaldato a temperatura
molto alta, viene separata da un prisma di vetro e proiettata su uno
schermo.
Un tipo diverso di spettro è prodotto dalla luce emessa da un gas
rarefatto, come l’idrogeno, quando viene attraversato da una scarica
elettrica o portato all’incandescenza.
Quando un sottile fascio di questa luce attraversa un prisma non si
ottiene uno spettro continuo ma discontinuo, o spettro a righe, nel
quale si osservano soltanto alcuni colori, distribuiti in una serie di righe
colorate e distinte che prende il nome di spettro atomico o spettro
di emissione.
Copyright © 2012 Zanichelli editore
3.2 GLI SPETTRI ATOMICI DIMOSTRANO CHE GLI ELETTRONI
POSSIEDONO ENERGIE QUANTIZZATE
La prima spiegazione quantitativa degli spettri atomici si deve allo
studio dello spettro dell’idrogeno, l’elemento più semplice con un solo
elettrone. Lo spettro atomico dell’idrogeno è costituito da diverse serie
di righe, una delle quali è nella regione visibile dello spettro
elettromagnetico. Un’altra serie di righe si trova nell’ultravioletto,
mentre le restanti stanno nell’infrarosso.
Copyright © 2012 Zanichelli editore
3.2 GLI SPETTRI ATOMICI DIMOSTRANO CHE GLI ELETTRONI
POSSIEDONO ENERGIE QUANTIZZATE
Nel 1885, Johann Jakob Balmer formulò un’equazione in grado di
descrivere le lunghezze d’onda delle righe presenti nella regione
visibile dello spettro dell’idrogeno.
La relazione fu successivamente rielaborata nell’equazione di
Rydberg, un’equazione empirica di validità generale che consentì di
calcolare le lunghezze d’onda di tutte le righe dello spettro
dell’idrogeno.
Nella formula λ è la lunghezza d’onda, RH è una costante
(109 678 cm-1), e n1 e n2 sono variabili che possono assumere valori
interi compresi tra 1 e 3. L’unico vincolo dell’equazione è che n2 deve
essere maggiore di n1.
Copyright © 2012 Zanichelli editore
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’ENERGIA DEGLI ELETTRONI È QUANTIZZATA
Il primo modello teorico dell’atomo di idrogeno in grado di
interpretare l’equazione di Rydberg fu proposto nel 1913 da Niels
Bohr (1885-1962), un fisico danese.
Nel suo modello, Bohr immaginò che l’elettrone si muovesse intorno
al nucleo seguendo traiettorie fisse, o orbite, come un pianeta che
ruota intorno al Sole. Infrangendo le leggi della fisica classica e
affidandosi invece alle nuove conoscenze introdotte dalla meccanica
quantistica di Planck, Bohr elaborò un’equazione che descriveva
l’energia di un elettrone in un atomo; il modello fissava le dimensioni
delle orbite e l’energia dell’elettrone di una data orbita.
c
Copyright © 2012 Zanichelli editore
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’EQUAZIONE DI BOHR GIUSTIFICA LE RIGHE SPETTRALI
DELL’IDROGENO
Copyright © 2012 Zanichelli editore
Esiste una semplice relazione tra la frequenza della luce e la sua
energia: E = hν.
Poiché gli atomi eccitati emettono luce di frequenze ben definite, al
loro interno devono avvenire solo variazioni di energia altrettanto
definite. Nello spettro dell’idrogeno, per esempio, esiste una riga
rossa che ha una lunghezza d’onda di 656,4 nm e una frequenza di
4,567 x 1014 Hz. Quindi, tutte le volte che un atomo di idrogeno
emette luce rossa, la frequenza della radiazione è sempre pari a
4,567x1014 Hz e l’energia dell’atomo diminuisce esattamente di
3,026 x 10-19 J per ciascun fotone, né più né meno. Gli spettri
atomici indicano pertanto che, quando un atomo eccitato libera
energia, la quantità liberata non assume valori qualsiasi; ciò è vero
anche quando l’atomo assorbe energia.
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’EQUAZIONE DI BOHR GIUSTIFICA LE RIGHE SPETTRALI
DELL’IDROGENO
In un atomo l’elettrone può assumere solo alcuni valori di energia
specifici e non altri. Possiamo affermare che l’elettrone è vincolato ad
alcuni livelli energetici e che l’energia dell’elettrone è
quantizzata.
L’elettrone può assumere soltanto energie corrispondenti ai vari livelli
energetici.
c
Copyright © 2012 Zanichelli editore
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’EQUAZIONE DI BOHR GIUSTIFICA LE RIGHE SPETTRALI
DELL’IDROGENO
Copyright © 2012 Zanichelli editore
Adesso siamo in grado di spiegare come prendono origine le righe
spettrali. Quando l’atomo assorbe energia, un elettrone passa da un
livello a bassa energia a uno di energia più alta; quando l’elettrone
ritorna allo stato di partenza, l’energia corrispondente alla differenza
fra i due livelli viene emessa come fotone.
Dato che sono possibili soltanto determinati salti energetici, nello
spettro di emissione compaiono solo alcune frequenze specifiche.
Da quanto si deduce dagli spettri atomici, l’esistenza di livelli
energetici specifici costituisce la base di tutte le teorie sulla struttura
elettronica.
c
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’EQUAZIONE DI BOHR GIUSTIFICA LE RIGHE SPETTRALI
DELL’IDROGENO
Oltre ad alcune costanti fisiche, come la massa dell’elettrone, la sua
carica e la costante di Planck, l’equazione di Bohr comprendeva
anche un numero intero n che egli chiamò numero quantico e che
può assumere tutti i valori interi da 1 a + ∞. Ciascuna orbita può
essere identificata in funzione del suo valore di n.
In particolare, il raggio in picometri (1 pm = 10-12 m) di ogni orbita
si può calcolare dalla relazione:
c
Copyright © 2012 Zanichelli editore
mentre l’energia associata a ogni orbita si ricava dalla seguente
relazione:
dove E è l’energia dell’elettrone, b una costante il cui valore è
2,18 10-18 J e n è il numero quantico
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►L’EQUAZIONE DI BOHR GIUSTIFICA LE RIGHE SPETTRALI
DELL’IDROGENO
A causa del segno negativo dell’equazione precedente, il valore più
basso (più negativo) di energia si ha quando n =1, che corrisponde
alla prima orbita di Bohr. Lo stato energetico più basso di un atomo è
anche il più stabile ed è chiamato stato fondamentale. Nel caso
dell’idrogeno, lo stato fondamentale è quello in cui il suo elettrone
possiede n =1.
c
Copyright © 2012 Zanichelli editore
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
►I SALTI ELETTRONICI DA UN’ORBITA ALL’ALTRA
COMPORTANO SCAMBI DI ENERGIA
Quando un atomo di idrogeno assorbe energia, come in un tubo a
scarica di gas, l’elettrone passa dall’orbita con n= 1 a un’orbita più
esterna, con n= 2 o n = 3 o ancora maggiore. Le orbite più lontane
dal nucleo sono meno stabili delle orbite più interne e l’elettrone
tende a tornare rapidamente nell’orbita a più bassa energia; quando
ciò accade l’energia viene emessa sotto forma di radiazione
elettromagnetica
c
Copyright © 2012 Zanichelli editore
3.3 IL MODELLO ATOMICO DI BOHR INTERPRETA
LO SPETTRO DELL’IDROGENO
► IL MODELLO DI BOHR SI DIMOSTRA INADEGUATO PER GLI
ALTRI ELEMENTI
Copyright © 2012 Zanichelli editore
Il modello atomico di Bohr fu allo stesso tempo un successo e un
fallimento. Ebbe pieno successo nel prevedere la frequenza delle
righe dello spettro dell’idrogeno, spiegando l’equazione di Rydberg.
D’altra parte, la teoria non riuscì a dare una spiegazione quantitativa
agli spettri degli atomi contenenti più di un elettrone. Con il tempo si
comprese che il modello di Bohr non era corretto e che sarebbe stato
necessario elaborare un altro modello atomico. Il concetto di numero
quantico e l’introduzione dei livelli di energia quantizzati
rappresentarono comunque un notevole progresso rispetto al
passato. Gli studi di Bohr per sviluppare una teoria sulla struttura
elettronica erano destinati a fallire sin dall’inizio perché le leggi della
fisica classica note a quel tempo non potevano essere applicate a
particelle così piccole come l’elettrone.
c
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
Gli elettroni all’interno degli atomi non si comportano come particelle
solide ma come onde. Questa intuizione fu proposta per la prima
volta nel 1924 da un giovane studente francese, Louis de Broglie.
Abbiamo visto che le onde sono caratterizzate da lunghezza d’onda
e frequenza. Lo stesso vale per le onde associate alla materia. De
Broglie suggerì che la lunghezza d’onda di un’onda associata a un
corpo in movimento, detta onda di materia, fosse espressa
dall’equazione:
Copyright © 2012 Zanichelli editore
Dove λ è la lunghezza d'onda, h la costante di Plank e mv è la
quantità di moto
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
L’idea che una particella di materia si comporti come un’onda è
difficile da comprendere. Nell’equazione di de Broglie la massa
compare al denominatore; ciò significa che, quanto maggiore è la
massa del corpo, tanto più piccola è la lunghezza dell’onda. Per i corpi
macroscopici, i massimi delle onde associate alla materia sono così
ravvicinati che le proprietà dell’onda passano inosservate e non
possono essere misurate sperimentalmente; al contrario, le particelle
minuscole, con massa ridottissima, hanno lunghezze d’onda maggiori
e le loro proprietà ondulatorie assumono un ruolo importante per
spiegarne il comportamento complessivo.
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
Le proprietà ondulatorie della materia possono essere dimostrate
osservando un fenomeno abbastanza comune.
Per esempio, le gocce di pioggia che cadono in uno specchio d’acqua
formano delle onde a partire dai punti in cui esse toccano l’acqua.
Quando due serie di onde si incrociano, vi sono alcuni punti in cui le
onde sono in fase, cioè i massimi di un’onda coincidono con i massimi
dell’altra: in questi punti le ampiezze delle onde si sommano. In altri
punti, le onde sono fuori fase: i massimi di un’onda coincidono con i
minimi dell’altra e le ampiezze delle due onde si annullano
reciprocamente.
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
Il rafforzamento e l’annullamento delle ampiezze delle onde sono
dovuti, rispettivamente, a interferenze costruttive e distruttive,
secondo un fenomeno che si chiama diffrazione. Quando le onde
attraversano una coppia di fenditure ravvicinate, si osserva che la
diffrazione crea caratteristiche frange di interferenza.
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
Le frange di interferenza più comunemente osservabili sono i colori
iridescenti che splendono sulla superficie di un compact disc.
La diffrazione è un fenomeno che può essere spiegato soltanto in
considerazione delle proprietà delle onde e abbiamo già visto come si
verifichi per le onde di uno specchio d’acqua e per quelle luminose. Si
possono condurre esperimenti per dimostrare che anche gli elettroni, i
protoni e i neutroni subiscono la diffrazione, a conferma della loro
natura ondulatoria. La diffrazione elettronica è, in effetti, il principio su
cui si basa la microscopia elettronica.
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► GLI ELETTRONI NEGLI ATOMI POSSIEDONO ENERGIE
QUANTIZZATE PERCHÉ SI COMPORTANO COME ONDE
STAZIONARIE
Copyright © 2012 Zanichelli editore
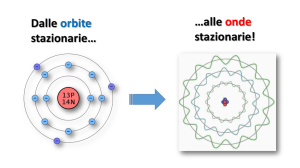
Con l’interpretazione dualistica dell’elettrone, che si avvale delle
conoscenze della meccanica ondulatoria, oltre che della meccanica
quantistica, l’elettrone è visualizzato non come una particella situata
in un punto dell’atomo, ma come se la sua massa e la sua carica
elettrica fossero distribuite in un’onda stazionaria che circonda il
nucleo. L’onda elettronica è chiamata funzione d’onda ed è di
norma rappresentata dal simbolo ψ (la lettera greca psi).
Nel 1926, Erwin Schrödinger (1887-1961), un fisico austriaco, fu il
primo a utilizzare con successo il concetto di natura ondulatoria della
materia per spiegare la struttura elettronica dell’atomo. Schrödinger
sviluppò un’equazione le cui soluzioni fornivano le funzioni d’onda e
lo stato energetico degli elettroni contenuti negli atomi. Le funzioni
d’onda relative agli elettroni atomici sono dette orbitali.
c
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► GLI ORBITALI SONO DESCRITTI DA TRE NUMERI QUANTICI
Come le caratteristiche di un’onda stazionaria possono essere
ricondotte a un solo numero intero, così la meccanica ondulatoria
consente di definire le onde elettroniche nelle tre dimensioni
(orbitali) mediante un insieme di tre numeri interi detti numeri
quantici: n, l, e ml. La classificazione degli orbitali secondo i numeri
quantici rende più semplice la discussione sulla loro energia.
c
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO PRINCIPALE, n
Copyright © 2012 Zanichelli editore
Il numero quantico n è detto numero quantico principale. Tutti gli
orbitali che hanno lo stesso valore di n appartengono allo stesso
livello (o strato). Il valore di n può assumere i valori interi da 1 a ∞;
il livello con n =1 è chiamato primo livello, quello con n = 2 secondo
livello, e così via. A volte i vari livelli sono indicati con lettere
maiuscole, iniziando (per convenzione) da K per il primo livello
(n =1), L per il secondo (n= 2) e così via.
Il numero quantico principale serve a determinare le dimensioni
dell’onda elettronica, cioè quanto essa si estende intorno al nucleo
dell’atomo. Quanto maggiore è il valore di n, tanto più grande è la
distanza media dell’elettrone dal nucleo. Il numero quantico
principale è correlato anche all’energia dell’orbitale: le energie degli
orbitali crescono all’aumentare di n. Il numero n compare anche
nell’equazione di Rydberg e nelle formule di Bohr.
c
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO SECONDARIO, l
Copyright © 2012 Zanichelli editore
Il numero quantico secondario, l, divide i livelli elettronici in gruppi
di orbitali, detti sottolivelli.
Il valore di n determina i possibili valori di l. Per un certo valore di n, l
può assumere valori da 0 a n -1: l= 0, 1, 2, …, n -1. Così,
per n =1, n - 1 =0 e il solo valore di l permesso è zero.
Ciò significa che, quando n =1, esiste solo un sottolivello (livello e
sottolivello coincidono).
Per n =2, l può essere 0 o 1, poiché il valore più grande di l =n - 1 è
2 -1 =1. Nel livello n = 2 esistono quindi due sottolivelli, uno
caratterizzato dai numeri quantici n = 2 e l =0, l’altro da n =2 e l = 1.
I sottolivelli sono chiaramente identificati dai valori di l ma, per evitare
confusione tra i valori numerici di n e l, il valore di l è preferibilmente
espresso con un codice letterale:
c
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO SECONDARIO, l
I sottolivelli sono chiaramente identificati dai valori di l ma, per evitare
confusione tra i valori numerici di n e l, il valore di l è preferibilmente
espresso con un codice letterale:
c
Copyright © 2012 Zanichelli editore
Per designare un particolare sottolivello, si scrive il valore del suo
numero quantico principale seguito dalla lettera minuscola
corrispondente al numero quantico secondario. Per esempio, il
sottolivello con n =2 e l =1 è il sottolivello 2p.
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO SECONDARIO, l
In base alla relazione fra n e l, ogni livello possiede un sottolivello s (1s,
2s, 3s, ecc.); tutti i livelli, eccetto il primo, possiedono un sottolivello p
(2p, 3p, 4p, ecc.); tutti, eccetto il primo e il secondo, possiedono un
sottolivello d (3d, 4d, ecc.) e così via.
c
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO SECONDARIO, l
Il numero quantico secondario determina la forma dell’orbitale, che
prenderemo in considerazione più avanti. A parte il caso dell’idrogeno,
che possiede un solo elettrone, il valore di l influenza anche l’energia
dell’orbitale. Negli atomi con due o più elettroni, i sottolivelli in un dato
livello possiedono energie leggermente diverse che aumentano
all’aumentare di l. Ciò significa che, in un dato livello, il sottolivello s è
quello con l’energia più bassa, seguito dai sottolivelli p, d, f e così via.
Per esempio:
c
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO MAGNETICO, ml
Il terzo numero quantico è noto come numero quantico magnetico.
Esso suddivide i sottolivelli in singoli orbitali e descrive l’orientamento
spaziale di un orbitale rispetto agli altri. Come nel caso di l, vi sono
limitazioni anche per i valori di ml, che possono variare da +l a -l
compreso lo zero.
Per l =0, ml può soltanto assumere valore zero. Un sottolivello s è
formato quindi da un solo orbitale. Quando l =1, i valori possibili di ml
sono +1, 0 e -1.
Un sottolivello p è formato quindi da tre orbitali: uno con l =1 e
ml =1, un altro con l =1 e ml =0 e l’ultimo con l = 1 e
ml =-1. Considerazioni analoghe indicano che un sottolivello d è
formato da cinque orbitali e un sottolivello f da sette. Il numero di
orbitali di un dato sottolivello è facile da ricordare perché segue una
semplice progressione aritmetica.:
c
l
l
l
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► IL NUMERO QUANTICO MAGNETICO, ml
Le relazioni tra i tre numeri quantici possono essere così riassunte::
c
Copyright © 2012 Zanichelli editore
3.4 LA CRISI DELLA MECCANICA CLASSICA PORTA AL
MODELLO ATOMICO A ORBITALI, O QUANTO-ONDULATORIO
► GLI ORBITALI SI DISTRIBUISCONO SECONDO VALORI DI
ENERGIA CRESCENTE
In generale gli orbitali si distribuiscono secondo valori di energia crescente
seguendo queste semplici regole:
1.Tutti gli orbitali di un dato sottolivello possiedono la stessa energia
2.Salendo nella scala dell’energia, la distanza fra livelli successivi
diminuisce mentre il numero dei sottolivelli aumenta. Ciò porta alla
sovrapposizione dei livelli che possiedono valori diversi di n. Per esempio, il
sottolivello 4s ha energia minore del sottolivello 3d, il 5s del 4d e il 6s del
5d. Inoltre, il sottolivello 4f precede il 5d e il 5f precede il 6d.:
c
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Un atomo è nel suo stato di massima stabilità (stato fondamentale)
quando i suoi elettroni hanno le minori energie possibili. Questo
avviene quando gli elettroni «occupano» gli orbitali disponibili a
energia più bassa.
Ma che cosa determina il modo in cui gli elettroni «riempiono» questi
orbitali?
Lo spin dell’elettrone è un fattore importante che ne influenza la
distribuzione.
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Quando un fascio di atomi contenenti un numero dispari di elettroni
viene diviso in due parti quando attraversa un campo magnetico
disomogeneo.
Questo fenomeno può essere spiegato immaginando che l’elettrone
ruoti intorno al proprio asse, come una trottola.
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
La carica elettrica dell’elettrone in movimento genera un debole
campo magnetico. Il movimento rotatorio, noto come spin
dell’elettrone, può avvenire in due sensi, orario e antiorario,
spiegando così la creazione dei due fasci
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Lo spin dell’elettrone è descritto dal quarto numero quantico,
chiamato numero quantico di spin, ms, che può assumere due
valori:
ms = +1/2 o ms = -1/2.
A noi non interessano i valori di ms, né il perché questi non siano
numeri interi; è, invece, molto importante il fatto che esistano solo
due valori di ms.
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Nel 1925, il fisico austriaco Wolfgang Pauli (1900-1958) chiarì
l’importanza dello spin dell’elettrone nella determinazione della
struttura elettronica dell’atomo.
Il principio di esclusione di Pauli stabilisce che nello stesso atomo
non possono esistere due elettroni che abbiano gli stessi valori dei
quattro numeri quantici.
Questo principio può essere riassunto nei seguenti punti:
1.ciascun orbitale non può contenere più di due elettroni;
2.gli elettroni che occupano lo stesso orbitale devono avere spin
opposto.
Copyright © 2012 Zanichelli editore
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Il limite di due elettroni per orbitale dà anche una misura del numero
massimo di elettroni presenti nei vari livelli e sottolivelli. Per i
sottolivelli abbiamo:
Il numero massimo di elettroni in ogni livello è invece:
Copyright © 2012 Zanichelli editore
In generale, la popolazione massima di elettroni in un livello è
pari a 2n2.
3.5 LO SPIN DELL’ELETTRONE INFLUENZA LA DISTRIBUZIONE
DEGLI ELETTRONI NEGLI ORBITALI
Alcuni atomi hanno elettroni spaiati, cioè non appaiati a elettroni
di spin opposto. In essi, gli effetti magnetici non si annullano e gli
stessi atomi si comportano come piccoli magneti che possono
interagire con un campo magnetico esterno. La debole attrazione
verso un magnete di una sostanza con elettroni spaiati è detta
paramagnetismo.
Le sostanze i cui atomi hanno tutti gli elettroni appaiati, invece, non
vengono attratte da un magnete e sono dette diamagnetiche
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Copyright © 2012 Zanichelli editore
La descrizione del moto degli elettroni all’interno di un atomo è
piuttosto complessa perché queste particelle si comportano anche
come onde: non esiste niente di paragonabile nella nostra esperienza
quotidiana.
La descrizione della posizione dell’elettrone in termini di probabilità
statistica si basa su qualcosa di più che una semplice convenzione
pratica. Werner Heisenberg, fisico tedesco, dimostrò
matematicamente che è impossibile misurare simultaneamente
la velocità e la posizione di una particella con assoluta precisione. Per
poter misurare la velocità o la posizione di un elettrone, è necessario
colpirlo con un’altra particella, per esempio un fotone: la conseguenza
è che la stessa misurazione altera la posizione e la velocità
dell’elettrone, con il risultato di rendere impossibile la determinazione
simultanea delle due grandezze, indipendentemente dall’efficienza del
sistema di misura.
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Questo fatto è noto come principio di indeterminazione di
Heisenberg. Le limitazioni teoriche appena descritte non riguardano gli
oggetti di grandi dimensioni ma solo le particelle minuscole come gli
elettroni, impedendoci di conoscerne con esattezza il comportamento
in un certo istante e costringendoci, così, a parlarne in termini di
probabilità.
Questo principio può essere espresso nel seguente modo:
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
L’idea di probabilità applicata al comportamento dell’elettrone conduce
ad altri due concetti molto importanti e comunemente utilizzati.
Secondo il primo, un elettrone si comporta come se fosse distribuito
attorno al nucleo in una specie di nube elettronica.
La figura mostra un diagramma di densità che illustra come varia la
probabilità di trovare un elettrone nello spazio per un orbitale 1s.
Dove si ha il maggior numero di punti per unità di volume, l’ampiezza
dell’onda è più grande e la probabilità di trovare l’elettrone è
maggiore.
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
L’altro importante concetto che emerge dalla variazione della
probabilità elettronica da un punto dello spazio all’altro è quello di
densità elettronica, che descrive la quantità di carica elettrica,
dovuta all’elettrone, presente in un dato volume. Nelle regioni ad alta
probabilità esiste un’elevata concentrazione di carica elettrica (e di
massa) e la densità elettronica è grande; nelle regioni a bassa
probabilità, la densità elettronica è minore.
Quando studiamo la distribuzione della densità elettronica negli
orbitali atomici, siamo soprattutto interessati a conoscere tre aspetti:
la forma dell’orbitale, le sue dimensioni e il suo orientamento nello
spazio rispetto agli altri orbitali.
Copyright © 2012 Zanichelli editore
La densità elettronica non si annulla in modo netto a una certa
distanza dal nucleo ma decresce sempre gradualmente. Così, per
definire la forma e le dimensioni di un orbitale, è utile pensare a una
superficie immaginaria che comprenda, per esempio, il 90% della
densità elettronica dell’orbitale stesso e sulla quale la probabilità di
trovare l’elettrone sia ovunque la medesima.
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Per l’orbitale 1s della si osserva che l’allontanamento a una data
distanza dal nucleo in una qualsiasi direzione comporta la stessa
probabilità di trovare l’elettrone.
Ciò significa che tutti i punti di uguale probabilità sono situati sulla
superficie di una sfera; possiamo perciò affermare che la forma
dell’orbitale 1s è sferica. Tutti gli orbitali s sono sferici e le loro
dimensioni aumentano al crescere di n. A cominciare dall’orbitale 2s,
vi sono regioni in cui la densità elettronica scende a zero; queste
corrispondono ai nodi dell’onda elettronica. Nelle onde elettroniche i
nodi sono superfici immaginarie sulle quali la densità elettronica è
nulla.
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Gli orbitali p diversi dagli orbitali s: la densità elettronica è distribuita
simmetricamente in due regioni opposte rispetto al nucleo.
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Come abbiamo visto, un sottolivello p è costituito da tre orbitali di
uguale energia. La meccanica delle onde ci suggerisce che la massima
densità elettronica dei tre orbitali si distribuisce lungo linee orientate
perpendicolarmente l’una rispetto all’altra, che corrispondono a un
sistema immaginario di coordinate xyz.
Per convenienza, gli orbitali p vengono spesso designati in base
all’asse che occupano: l’orbitale p concentrato intorno all’asse x è
indicato come px, e così via. Anche per gli orbitali p, la grandezza
aumenta all’aumentare di n.
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
La forma degli orbitali d, è più complessa di quella degli orbitali p. Per
tale motivo, e poiché esistono cinque orbitali in ogni sottolivello d,
questi non sono rappresentati contemporaneamente sugli stessi assi.
Copyright © 2012 Zanichelli editore
3.6 DOVE L'ELETTRONE PASSA IL SUO TEMPO
Gli orbitali f sono ancora più complessi degli orbitali d. Per ogni
sottolivello se ne hanno addirittura 7. Come vedremo, gli orbitali f
saranno riempiti tipicamente da elementi delle serie di transizione
interna (lantanidi e attinidi).
Copyright © 2012 Zanichelli editore