Esercizi di meccanica svolti a lezione

L’energia potenziale della forza di
gravitazione universale - la velocità di fuga
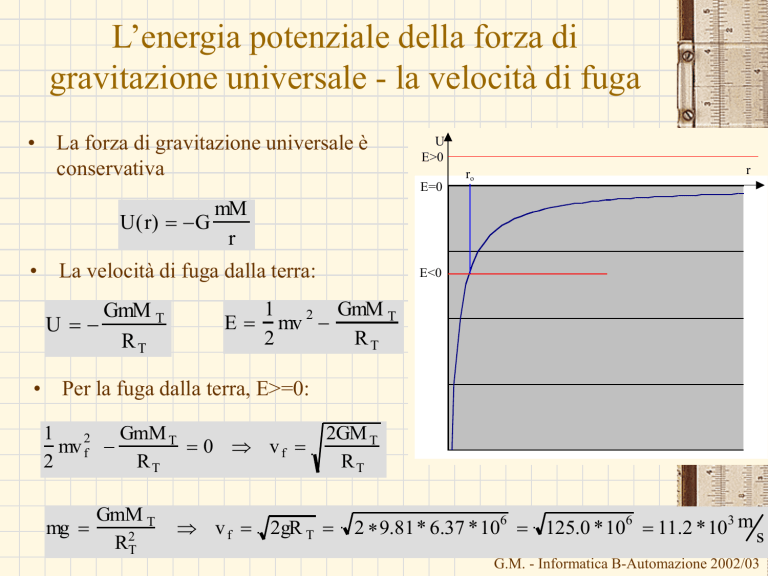
• La forza di gravitazione universale è
conservativa
U
E>0
E=0
U(r)  G
GmM T
RT
r
mM
r
• La velocità di fuga dalla terra:
U
ro
E
E<0
1
GmM T
2
mv 
2
RT
• Per la fuga dalla terra, E>=0:
1
GmM T
2
mv f 
 0  vf 
2
RT
mg 
GmM T
R2T
2GM T
RT
 v f  2gR T 
6
6
3
2 9.81* 6.37 *10  125.0 *10  11.2 *10 m s
G.M. - Informatica B-Automazione 2002/03
Il centro di massa del sistema terra-sole
mt
ms
xs
O
x
xt
n
m x
i i
i1
xCM =
n
x CM
M
m y
i i
y CM =
i1
n
M
m z
0
i i
z CM =
•
•
i1
M
0
= m sxs + m tx t
ms + mt
dove
m s = 2 1030 Kg;
d ts = 1.5 1011 m
m t = 6 1024 Kg
x CM 
m S xS  m T x T  m TxS  m Tx S

mS  mT
d CM S 
mT
dT S
mS  mT
 xS 
m T x T  xS 
mT
 xS 
d TS
mS  mT
mS  mT
d CM T 
mS
dT S
mS  mT
Il centro di massa si trova sul segmento
che congiunge i due punti materiali
È più vicino al punto materiale di massa
maggiore
d CM S 
dCM S m T

d CM T
mS
6x102 4
11
5
1.5x10

4.5x10
m
2x103 0  6x10 2 4
G.M. - Informatica B-Automazione 2002/03
•
Tre masse uguali sono ai vertici di un triangolo equilatero di lato L.
Determinare la posizione del centro di massa
y
3
x CM 
L
1
1 (0,0)
2
y CM
3 (L cos 60, Lsen 60)
1
2
x
CM12
m y  m 2y 2  m3 y3 m0  0  L sen60
 1 1


m1  m 2  m3
3m
3 L
3L
2

3
6
Posso determinare prima il centro di massa delle particelle 1 e 2.
m x  m2 x 2
x  x2 L
x CM1 2  1 1

xCM 1 2  1

se
m
m
m1  m 2
2
2
1
2
Calcoliamo ora la posizione del CM della particella 3 e di una
particella di massa 2m posta nella posizione del CM delle
particelle 1 e 2.
L
x

CM
Il centro di massa si troverà sulla congiungente:
2
3
1
m1x1  m2x 2  m3 x3 m0  L  L cos60 1.5  L L



m1  m2  m3
3m
3
2
x
2 (L,0)
y
Applic
azione
x
y CM 
2m  0  mL 3 

2 
3m

3 L
3L
2

3
6
G.M. - Informatica B-Automazione 2002/03
•
L’elemento oscillante di un pendolo è costituito da una sbarretta di massa
ms=0.5kg e lunga 50 cm a cui è attaccata un disco di massa md=1kg di 20cm
di diametro. Determinare la posizione del CM.
y
y
•
•
Applic
azione
CM della sbarra (0,0.45m) ms=0.5kg
CM del Disco (0,0.1m) md=1kg
x CM  0
x
x
m1y1  m2y 2 1kg  0.1m  0.5kg  0.45m 0.1  0.225kgm 0.325
y CM 



m  0.22m
m1  m2
1.5kg
1.5kg
1.5
G.M. - Informatica B-Automazione 2002/03
•
Nella figura si vede una piastra quadrata di lamiera uniforme con lato di 6m,
dalla quale è stato ritagliato un pezzo quadrato di 2 m di lato con centro nel
punto x=2m,y=0m L’origine delle coordinate coincide con il centro della
piastra quadrata. Trovare le coordinate x e y del CM.
y
•
CM
CM2
CM1
•
•
•
CM Intera piastra (0,0 m) M
CM1 incognito (?,0) m1=(36-4)/36M=8/9M
CM2 (2,0) m2=1/9M
x CM
x
Applic
azione
Per ragioni di
simmetria
y CM  0
8
1
Mx

Mx 2
1
m 1x1  m 2x 2 9
9


0
m1  m 2
M
8
1
Mx 1  Mx 2  0 
9
9
x1  
x2
 0.25m
8
G.M. - Informatica B-Automazione 2002/03
•
Determinare la posizione del centro di massa di un semidisco omogeneo di
massa M e raggio R.
x CM  0 per ragioni di simmetria
y
•
y+dy
y

M
R 2
y CM 
•
q
x
•
2

corp o


dm

4M
cos qydy
R
corp o
M
y  Rsen q
4

R
 cos qydy
corp o
corp o
y CM 
4R



2
0
cos qsen qdq 
2
Dividiamo il semicerchio in strisce
molte sottili
Sostituiamo ciascuna striscia con il
suo centro di massa (0,y)
Associamo a ciascun CM parziale
la massa dell’intera striscia.
4M
cos qdy
R
 dm  2R cos qdy 
dm y
Applic
azione
dy  R cosqdq
y CM 
4
R
 cos qRsen qRcos qdq
corp o

2
4R  cos q
4R 0 1  4R




 .424R



 
3

3
3
3

0
3
G.M. - Informatica B-Automazione 2002/03
•
Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il verde
(t=0s) parte con una accelerazione costante di 4 m/s2. Nello stesso istante
sopraggiunge con velocità costante di 8m/s un camion di massa 2000kg che
sorpassa l’auto. A che distanza dal semaforo si troverà il centro di massa del
sistema auto camion per t=3.0s?
x C  vC t  x C  24m
Quale sarà la sua velocità?
t3s
t=0
xa 
x
O
t=3s
O
x
1 2
at
2
v C  vC
v a  at

t3s
x a  18m

v C  8m / s

va  12m / s
t 3s
t 3s
Applic
azione
x CM (3s) 
m C x C  m a x a 2000  24  1000  18

m  22m
mC  ma
3000
v CM (3s) 
m C v C  m a va 2000  8  1000  12 m
m

 9.3
mC  ma
3000
s
s
a CM (3s) 
m Ca C  ma a a 2000  0  1000  4 m
m


1.33
mC  m a
3000 B-Automazione
s2 2002/03
s2
G.M. - Informatica
•
Un’auto di massa 1000 kg è ferma ad un semaforo. Quando viene il verde
(t=0s) parte con una accelerazione costante di 4 m/s2. Nello stesso istante
sopraggiunge con velocità costante di 8m/s un camion di massa 2000kg che
sorpassa l’auto. A che distanza dal semaforo si troverà il centro di massa del
sistema auto camion per t=3.0s?
Quale sarà la sua velocità?
Applic
azione
t=0
x
O
1
x CM  v CM t  a CM t 2
2
v CM (t)  v CM (0s)  at

t3s

t3s
x CM (0s)  0m
v CM (0s) 
m C vC  ma va 2000  8  1000  0 m
m

 5.33
mC  m a
3000
s
s
a CM (0s) 
m C a C  m a a a 2000  0  1000  4 m
m


1.3
2
2
mC  ma
3000
s
s
1
xCM  5.33  3  1.33  9  22.0m
2
vCM (3s)  5.33  1.33x3  9.33m / s
G.M. - Informatica B-Automazione 2002/03
•
Un’astronave di massa totale M sta viaggiando nelle profondità dello spazio
con una velocità vi=2100km/h rispetto al sole.
Espelle uno stadio posteriore di massa 0.20M alla velocità relativa
u=500km/h rispetto all’astronave, diretta lungo l’asse x.
Quanto diventa la velocità dell’astronave rispetto al sole?
Applic
azione
Indichiamo con U la velocità dello
stadio posteriore rispetto al sole.
Siamo molto lontani da qualsiasi altro
corpo, quindi le forze esterne sono nulle.
La quantità di moto si conserva.
Consideriamo il sole come un sistema di
riferimento inerziale
dP
=0
dt

P  costante
Pi  Pf
La quantità di moto iniziale è diretta lungo l’asse x
La quantità di moto finale dello stadio posteriore è anch’essa diretta lungo l’asse x
Anche la quantità di moto del resto dell’astronave sarà diretta lungo l’asse x
Pix  Pfx  Mv i  0.20M  U  0.80M  vf
Mvi  0.20M  v f  u  0.80M  vf
v  v' vO'
U  u  v f
 Mvi  Mvf  0.20Mu
km
km
v f  v i  0.20u  2100 km
h  0.20  500 h  2200 h
G.M. - Informatica B-Automazione 2002/03
•
Nella figura si vede un vagone ferroviario a pianale basso di massa M che è
libero di muoversi senza attrito su un binario rettilineo orizzontale.
Applic
All’inizio un uomo di massa m sta fermo sul vagone che viaggia verso destra
azione
con velocità vo. Quale sarà la variazione di velocità del vagone se l’uomo si
metterà a correre verso sinistra con una velocità vrel rispetto al vagone?
Si assuma vo=1m/s, vrel=5m/s, m=70kg, M=1000kg.
In questo caso le forze esterne non sono nulle:
peso del vagone, peso dell’unomo, reazione
vincolare del binario (solo componente
normale).
Però le forze sono tutte verticali
Si conserva la quantità di moto orizzontale, in
x
particolare quella diretta secondo i binari.
Il sistema di riferimento è quello dei
binari (inerziale).
Pix  Pfx
dPx
est
= Rx = 0
dt

Px  costante
 M  m vi  mv u  Mv f vu velocità dell’uomo rispetto ai binari
Dai moti relativi
v  v' vO'
v u  v rel  v f
M  mvi  m  vf  v rel   M  vf  M  mv i  M  mv f  mv rel
vf 
mM
m
70 m 1140
vi 
v rel  1 ms 
5s 
mM
m M
1070
1070
m
s
 1.07 ms
G.M. - Informatica B-Automazione 2002/03
•
Un bastone assimilabile ad una sbarretta omogenea di massa m0.5kg e
lunghezza L=1m. Inizialmente il bastone ha n estremo a contatto con il
pavimento e viene lasciato cadere partendo da una posizione pressoché
verticale. Determinare il lavoro fatto dalla forza peso.
y
Applic
azione
Posizione iniziale
Posizione finale
x
WP = UP

WP = U Pf  U Pi   U Pi  U Pf
Scegliendo come piano orizzontale a cui attribuire energia potenziale zero il
piano y=0, otteniamo
WP  UPi  U Pf
L
U Pi  mg
2
U Pf  0

WP  U Pi  U Pf  mg
L
 0.5kg  9.81 m2  0.5m  2.45J
s
2
G.M. - Informatica B-Automazione 2002/03
•
y
L’elemento oscillante di un pendolo, di cui abbiamo già determinato la
posizione del CM, è costituito da una sbarretta di massa ms=0.5kg e lunga 50
cm a cui è attaccata un disco di massa md=1kg di 20cm di diametro.
Esso è libero di ruotare attorno ad un asse passante per l’estremo libero della
sbarretta. Supponendo di lasciarlo cadere quando la sbarretta è orizzontale,
determinare il lavoro fatto dalla forza peso nello spostamento dalla posizione
iniziale alla posizione in cui la sbarretta è verticale
Posizione iniziale
Applic
azione
x
WP = UP

WP = U Pf  U Pi   U Pi  U Pf
Posizione finale
Il pendolo poi prosegue oltre questa posizione (in
assenza di attriti raggiunge la posizione simmetrica a
quella di partenza rispetto all’asse di rotazione e poi
ritorna indietro e oscilla tra la posizione iniziale e quella
simmetrica rispetto all’asse di rotazione)
G.M. - Informatica B-Automazione 2002/03
•
y
L’elemento oscillante di un pendolo, di cui abbiamo già determinato la
posizione del CM, è costituito da una sbarretta di massa ms=0.5kg e lunga 50
cm a cui è attaccata un disco di massa md=1kg di 20cm di diametro.
Esso è libero di ruotare attorno ad un asse passante per l’estremo libero della
sbarretta. Supponendo di lasciarlo cadere quando la sbarretta è orizzontale,
determinare il lavoro fatto dalla forza peso nello spostamento dalla posizione
iniziale alla posizione in cui la sbarretta è verticale
Posizione iniziale
Applic
azione
x
WP = UP
WP = U Pf  U Pi   U Pi  U Pf

Ricordando il calcolo della posizione del CM già fatto
nella lezione precedente d1=.22m
Scegliendo come piano orizzontale a
cui attribuire energia potenziale zero
il piano y=0, otteniamo
WP  UPi  U Pf
U Pi  0

U Pf   ms  m d gd 2
WP  UPi  U Pf  0  m s  m d gd 2   1.5kg  9.81 m2  0.48m  7.06J
s
G.M. - Informatica B-Automazione 2002/03
•
Una maniera alternativa per arrivare allo stesso risultato parte
dall’osservazione che l’energia potenziale di un sistema di punti materiali si
ottiene sommando le energie potenziali delle singole particelle:
WP = UP

Applic
azione
WP = U Pf  U Pi   U Pi  U Pf  U Psi  U Pdi   UPsf  U Pdf 
y
x
U Psi  0
U Psf
L
  ms g
2
U Pdi  0
U Pdf   ms gL  R
WP  UPi  U Pf
U Pi  0
U Pf   ms  m d gd 2

L

WP  U Psi  U Pdi   U Psf  U Pdf   0  m sg  m d gL  R 
 
2
 0.5kg  9.81 m2  0.25m  1.0kg  9.81 m2  0.60m 
s
s
 9.810.5  0.25  1.0  0.60 J  9.810.5  0.25  1.0  0.60  9.810.725J  7.11J
Che, a parte errori di arrotondamento, è uguale al valore trovato con l’altro metodo.
G.M. - Informatica B-Automazione 2002/03
•
Una pallottola da 30 g, con velocità iniziale di 500 m/s penetra per 12 cm in
una parete di muratura prima di fermarsi
Di quanto si riduce l’energia meccanica della pallottola?
Qual è la forza media che ha agito sulla pallottola mentre penetrava nella
parete?
Quanto tempo ha impiegato la pallottola per fermarsi?
Prima
Usiamo il sistema di riferimento del Laboratorio
per descrivere il moto:
la parete è ferma in tale sistema
il sistema di riferimento è inerziale
Le forze agenti sono:
La forza peso (fa lavoro nullo)
La Normale (fa lavoro nullo)
La forza di attrito(dinamico)
Applic
azione
x
Dopo
L’energia meccanica totale coincide con
l’energia cinetica.
Nell’ipotesi di un moto orizzontale come
mostrato in figura, non c’è variazione
dell’energia potenziale della forza peso
Kf  0
1
1
2
3
2
1 2
E  K f  Ki   mv i    30  10  500  3750J
K i  mv i
2
2
2
E
3750
3
P

mg

30

10
 9.81  .294N
E  Wnc  Fx x  Fx 


31250N
2
x 12  10
E  Ef  Ei  Kf  Ki
Circa 100 mila volte il peso
G.M. - Informatica B-Automazione 2002/03
•
Per calcolaci tempo ha impiegato dalla pallottola per fermarsi, valutiamo
l’impulso della forza.
Prima
I  p  pf  pi
Applic
azione
x
La quantità di moto finale è nulla
Quella iniziale ha solo la componente x
Anche l’impulso avrà solo la componente x
I x  p x f  px i  mv i  30  10
I x  Fx t  t 
3
Dopo
 500  15kgms
1
Ix
15

 0.032s
Fx 31250
Il proiettile impiega 3.2 centesimi di secondo per fermarsi
Questo semplice esempio mostra come
le forze negli urti siano molto intense
I tempi dell’interazione siano piuttosto piccoli
G.M. - Informatica B-Automazione 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Determinare la perdita di energia meccanica nell’urto.
Determinare l’elongazione massima del pendolo
Se la pallottola è penetrata nel pendolo per un tratto di 3cm, stimare la forza
media che ha frenato la pallottola rispetto al blocco e la durata dell’urto
verificare che lo spostamento subito dal pendolo durante l’urto è trascurabile.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
mv
30  10 3 kg  500 m s
Vx 

 3.72 m s
M m
4.030kg
Applic
azione
O
1 2 M
1
4.
3
2
mv
 30  10  500

2
M m 2
4.030
 3750  .993  3696.0J
K persa 
m
v
M
K  K f  Ki   Kp ersa  Wfa  Fa x
Kp ersa
3696.0
Fa 

2  123201N
x
3  10
p1f  p1i 30  1033.72  500
t 

 0.12  10 3 s
Fax
123201N
3
3
d  Vx t  3.72 m s  .12  10 s  .44  10 m
G.M. - Informatica B-Automazione 2002/03
II fase oscillazione
• L’oscillazione avviene sotto l’azione della forza peso
(conservativa) e della tensione.
E  Wn c  WT
O
q
h  (1 cosq)
T
U f  M  mgh  M  mg (1 cosq)
h
dr
M +m
Ei  Ef
P M m
Ki  U i  Kf  U f
1
M  m Vx2  0  0  M  m g 1  cos q
2
1 m 2v 2
 M  m g 1  cos q
2 Mm
v
Vx 
mv
M m
M m
2g 1  cos q
m
G.M. - Informatica B-Automazione 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Determinare la perdita di energia meccanica nell’urto.
Determinare l’elongazione massima del pendolo
Se la pallottola è penetrata nel pendolo per un tratto di 3cm, stimare la forza
media che ha frenato la pallottola rispetto al blocco e la durata dell’urto
Verificare che lo spostamento subito dal pendolo durante l’urto è trascurabile.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
mv
30  10 3 kg  500 m s
Vx 

 3.72 m s
M m
4.030kg
Applic
azione
O
Ei  Ef
Ki  U i  Kf  U f
1
M  m Vx2  0  0  M  m g 1  cos q
2
 1 Vx2   1 3.722 
  1 
 .6473
cos q  1
 2 g   2 9.81  2 
m
v
M
q  ar cos.6473  50
G.M. - Informatica B-Automazione 2002/03
•
Una pallottola da m=30 g, viene sparata orizzontalmente con velocità di 500
m/s contro un blocco di legno di massa M=4kg appeso ad una fune di
lunghezza L=2m. La pallottola si conficca nel blocco e forma un tutt’uno con
esso.
Valutare infine la tensione nella fune subito prima e subito dopo l’urto.
y
Prima dell’urto:
T  P  0  T  P
Applic
azione
O
T  Mg  4  9.81  39.24N
Subito dopo l’urto, il pendolo è rimasto nella
stessa posizione, ma si sta muovendo con
velocità Vx:
T  P  M  ma
m
v
M
Proiettando su un asse verticale:
T  M  m g  M  m 
T  M  m g  M  m 
Vx2
Vx2
2

3.72


  46.45N
 4.030 9.81 

2 
G.M. - Informatica B-Automazione 2002/03
Urto in due dimensioni
• Consideriamo un urto in cui una della due
particelle è ferma (senza forze esterne)
– Particella 1 proiettile
– Particella 2 bersaglio
– b parametro d’urto
v1
m1
b
m2
• La retta di azione della velocità v1 e il punto P2
definiscono un piano
– Le forze di interazione sono lungo la congiungente
– Quindi contenute nel piano
– Non c’è moto perpendicolarmente al piano
precedentemente individuato (accelerazione nulla,
velocità iniziale nulla)
P1i  P2 i  P1f  P2 f
y
• L’urto è piano.
v' 1
m1v1  m1v' 1 cosq1  m2 v' 2 cosq2
0  m1v' 1 senq1  m2 v' 2 sen q2
Se l’urto è elastico
si può aggiungere:
1
1
1
2
2
2
m1v1  m1v' 1  m 2 v' 2
2
2
2
q1
v1
m1
m2
x
q2
v' 2
G.M. - Informatica B-Automazione 2002/03
Urto centrale elastico-bersaglio fermo
• Per risolvere il sistema conviene metterlo in questa
forma:
Urto centrale
v1
m 1v1x  v' 1x   m 2 v' 2 x
m 1v1x  m 1v' 1x m 2 v' 2 x
1
1
1
m1v21x  m1v' 21x  m 2 v' 22x
2
2
2


P1i  P2 i  P1f mP22 f
m1
x
m 1 v1x  v' 1x  m 2 v' 2 x
2
2
2
• Dividendo membro a membro la seconda per la prima:
m 1v1x  v' 1x   m 2 v' 2 x
v
1x

 v' 1x  v' 2 x
v
1x


 v' 1x  v' 2 x
m 1  m 2 
m 1  m 2 

m  m 2 
v1x  v1x  1
  v' 2 x

m1  m 2 
v' 1x  v1x

m 1v1x  v' 1x   m 2 v1x  v' 1x
v1x m1  m 2   v' 1x m1  m 2 
v
1x
v' 1x  v1x
m 1  m 2 
m 1  m 2 
v' 2 x  v1x
2m 1
m1  m 2 

 v' 1x  v' 2 x
G.M. - Informatica B-Automazione 2002/03
•
•
•
Due automobili A e B di massa rispettivamente 1100 kg e 1400 kg, nel
tentativo di fermarsi ad un semaforo, slittano su una strada ghiacciata. Il
coefficiente di attrito dinamico tra le ruote bloccate delle auto e il terreno è
0.13. A riesce a fermarsi, ma Be che segue, va a tamponare il primo veicolo.
Come indicato in figura, dopo l’urto A si ferma a 8.2 m dal punto di impatto e
B a 6.1 m. Le ruote dei due veicoli sono rimaste bloccate durante tutta la
slittata.
Determinare le velocità delle due vetture subito dopo l’impatto.
E la velocità della vettura B prima dell’urto.
Applic
azione
K  WP  WN  WFa  WFa
0
WFa  Fax  mg x
1
2
K f  Ki  0  mv  mgx
2
N
v  2gx
v A  2  0.13  9.81  8.2  4.6 m s
v B  2  0.13  9.81  6.1  3.9 m s
m B vo  m B vB  m A v A
 vo 
P
Fa
m B vB  m A vA 1400  3.9  1100  4.6

 7.5 m S
mB
1400
G.M. - Informatica B-Automazione 2002/03
Urto centrale elastico-bersaglio mobile
•
•
In questo caso sia la velocità della particella 1 che quella
della particella 2 sono dirette lungo la congiungente le due
particelle.
Considerando le componenti delle velocità lungo l’asse x:
m1v1x  m2 v2x  m1v' 1x m2 v' 2x
1
1
1
1
2
2
2
2
m1v1x  m 2 v2 x  m1v' 1x  m 2 v' 2x
2
2
2
2
•
Urto centrale
v1
v2
x
P1i  P2 i  P1f mP22 f
m1
m 1v1x  v' 1x   m 2 v' 2x v 2x 



2
m 1 v1x
 v' 21x  m 2 v' 22x v 22x

Operando come nel caso precedente, dividendo membro a membro la
seconda per la prima si perviene al seguente risultato:
v' 1x  v1x
m1  m 2
2m 2
 v2 x
m1  m 2
m1  m2
v' 2 x  v1x
2m1
m  m1
 v2 x 2
m1  m2
m1  m 2
•
Se le particelle hanno la stessa
massa, nell’urto si scambiano le
velocità
m1  m2 
v' 1x  v2 x
v' 2 x  v1x
G.M. - Informatica B-Automazione 2002/03
•
Un blocco di massa m1=2.0 kg scivola su di un pinao privo di attrito alla
velocità di 10 m/s. Davanti a questo blocco, sulla stessa linea e nello stesso
verso, si muove a 3.0 m/s un secondo blocco, di massa m2=5.0kg. Una molla
priva di massa , con costante elastica k=1120 N/m, è attacata sul retro di m2.
Qual è la massima compressione della molla quando i due blocchi si urtano?
Quali sono le velocità finale dei due corpi dopo l’urto.
•
•
•
–
–
–
–
Applic
azione
Quando la molla è alla sua
massima compressione i due
blocchi sono fermi uno rispetto
all’altro
Prima della massima compresione si sono avvicinati
Successivamente si allontanano
La velocità comune dei due blocchi sarà uguale a quella del centro di massa
Poiché la quantità di moto si conserva, anche la velocità del centro di massa sarà
uguale a quella iniziale:
m v  m 2 v2 2.0  10  5.0  3 35.0
v' 1  v' 2  vCM  1 1


 5ms
m1  m2
7.0
7.0
– La differenza tra l’energia cinetica iniziale e quella finale è
immagazzinata come compressione della molla
m1v12  m2 v 22  m1  m2 v 2CM
1
1
1
1
2
2
2
2 x 
m1v1  m 2v 2  m1  m 2 vCM  k x 
k
2
2
2
2
G.M. - Informatica B-Automazione 2002/03
•
•
•
Un blocco di massa m1=2.0 kg scivola su di un pinao privo di attrito alla
velocità di 10 m/s. Davanti a questo blocco, sulla stessa linea e nello stesso
verso, si muove a 3.0 m/s un secondo blocco, di massa m2=5.0kg. Una molla
priva di massa , con costante elastica k=1120 N/m, è attacata sul retro di m2.
Qual è la massima compressione della molla quando i due blocchi si urtano?
Quali sono le velocità finale dei due corpi dopo l’urto.
Applic
azione
– Da cui
x 
x 
m1v12  m2 v 22  m1  m2 v 2CM
k
2  100  5  9  7  25
70
1
1


  .25m
1120
1120
16 4
– Utilizzando le espressioni per l’uro centrale elastico:
v' 1x  v1x
v' 2 x  v1x
m1  m 2
2m 2
3
10
 v 2x
 10
 3.0
 0 ms
m1  m 2
m1  m 2
7
7
2m 1
m  m1
4
3 49
 v 2x 2
 10  3.0 
 7ms
m1  m 2
m1  m 2
7
7
7
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
•
•
•
Un volano di diametro di 1.20 m gira a velocità angolare di 200giri/min
Qual è la sua velocità angolare in rad/s?
Qual è il modulo della velocità lineare di un punto del bordo del volano?
Qual è l’accelerazione centripeta di un punto sul bordo del volano?
Qual è l’accelerazione angolare costante necessaria per portare a 1000 giri/min
in 60 s la velocità angolare del volano?
Qual è l’accelerazione tangenziale di un punto del bordo del volano?
Quanti giri compirà in questi 60 s?
diametro
R
 .60m
2

Applica
zione
200giri 200  2 rad

 20.9 rad
s
min
60s
m
v   R  20.9 rad
s  .60m  12.55 s
m
a c   2 R  20.9 rad

.60m

262.1

s
2
2
s
f 
1000giri 1000  2 rad

 104.7 rad
s
min
60s
   o  t
 f   o 104.7  20.9


 1.397 rad
2
s
t
60
m
rad
a t  R  1.397 2  .60m  .84 2
s
s
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
•
•
•
Un volano di diametro di 1.20 m gira a velocità angolare di 200giri/min
Qual è la sua velocità angolare in rad/s?
Qual è il modulo della velocità lineare di un punto del bordo del volano?
Qual è l’accelerazione centripeta di un punto sul bordo del volano?
Qual è l’accelerazione angolare costante necessaria per portare a 1000 giri/min
in 60 s la velocità angolare del volano?
Qual è l’accelerazione tangenziale di un punto del bordo del volano?
Quanti giri compirà in questi 60 s?
q  qo  ot  12 t
Applica
zione
2
q  qo   ot  12 t 2 
20.9  60  12 1.397  602  1254  2414 
 3668rad
3668rad 
giro
 583.79giri
2rad
G.M. - Informatica B-Automazione 2002/03
Momento di inerzia di un punto
materiale di massa M
• Consideriamo la situazione in figura:
• Applichiamo la definizione:

M
R
1
I

m i R2i  MR2
i1
G.M. - Informatica B-Automazione 2002/03
Momento di inerzia di un anello omogeneo di
massa M e raggio R rispetto al proprio asse
• Consideriamo la situazione della figura:
• Supponiamo che l’anello ruoti attorno un asse,
perpendicolare all’anello passante per il suo centro (asse
dell’anello).
M
l

• Indichiamo con l la densità lineare dell’anello:

M
R
2R
• Consideriamo un elemento dell’anello: d  Rd
•
M
M
Rd 
d
a cui corrisponde la massa: dm  ld 
2R
2
y
R
d
d
x
• Applichiamo la definizione di momento di inerzia per i corpi
continui:
M 2 2
M 2 2 M 2
2
M
I
R d 
R  0 
R 2  0  MR 2
2
2
I  dm R 
dR
2
2
2
0
anello
0 2



• I=MR2 come se la massa dell’anello fosse concetrata in un
punto materiale a distanza R dall’asse.
G.M. - Informatica B-Automazione 2002/03
Momento di inerzia di un disco omogeneo di
massa M e raggio R rispetto al proprio asse
• Consideriamo la situazione di figura:
• Supponiamo che il disco ruoti attorno un asse, perpendicolare
al disco passante per il suo centro (asse del disco).
M


• Indichiamo con  la densità superficiale del disco:
R 2
• Suddividiamo il cerchio in tante corone circolari infinitesime
e concentriche di spessore dr. A tutti gli effetti può essere
considerato un anello di massa:
M
2M
dm  dS 
R
2
2rdr 
R
2
rdr
• a cui corrisponde un momento di inerzia:
dI  dmr 
2
2M 3
2 r dr
R
• Applichiamo la definizione di momento di inerzia per i corpi
continui:
I
 dI  
corp o
R
0
R
4
2M 3
2M r 4  2M 
R
  0
  1 MR2
r
dr


2
R2
R 2 
 2
4 
0 R  4
G.M. - Informatica B-Automazione 2002/03
Momento di inerzia di un cilindro omogeneo
di massa M e raggio R e altezza h rispetto al
proprio asse

• Consideriamo la situazione di figura:
• Supponiamo che il cilindro ruoti attorno al proprio asse.
M
• Indichiamo con r la densità del cilindro:
r
M
R
R
R h
2
• Suddividiamo il cerchio in tanti strati infinitesimi
infinitesime di altezza dz. A tutti gli effetti ogni strato può
essere considerato un disco di massa:
dm  rdV 
M
M
2
R
dz

dz
2
R h
h
• a cui corrisponde un momento di inerzia:
dI 
1
1M
2
2
dmR 
dzR
2
2 h
h
• Applichiamo la definizione di momento di inerzia per i corpi
continui:
h
I

dI 
corp o
• Come il disco

0
z

M
R
R
z=h
z+dz
z
z=0
1M 2
1 M 2 h 1M 2
1
R dz 
R z0 
R h  0  MR 2
2 h
2 h
2 h
2
G.M. - Informatica B-Automazione 2002/03
Sbarra di lunghezza L e massa M ruotante
rispetto ad un asse passante per un estremo
• Consideriamo la situazione della figura:
• Supponiamo che la sbarra ruoti attorno un asse,
perpendicolare alla sbarra passante per un suo
estremo.
M
• Indichiamo con l la densità lineare della sbarra. l 
L
M
L
l
M
L
z
• Introduciamo un sistema di riferimento come in figura
• Suddividiamo la sbarra in elementi infinitesimi di
lunghezza dx,
– indichiamo con x la coordinata del primo estremo
dell’elemento infinitesimo
– La distanza dell’elemento infinitesimo dall’asse di
rotazione sarà proprio il valore assoluto di x.
L
R=x
x
x+dx
dm  ldx 
M
x
M
dx
L
L
3
M L2
M x3 
M 
L
1
2
2
  0
  ML 2
I  dmR  ldx x 
x dx    
L 0
L  3 0 L  3
 3
sbarra
0


L

G.M. - Informatica B-Automazione 2002/03
Sbarra di lunghezza L e massa M ruotante
rispetto ad un asse passante per il centro
• Consideriamo la situazione della figura:
• Supponiamo che la sbarra ruoti attorno un asse,
perpendicolare alla sbarra passante per il suo centro.
M
• Indichiamo con l la densità lineare della sbarra. l 
l
L
• Introduciamo un sistema di riferimento come in figura
• Suddividiamo la sbarra in elementi infinitesimi di
lunghezza dx,
M
L
M
L
z
M
L R=|x|
L

2
x x  dx
x
L
2
– indichiamo con x la coordinata del primo estremo
dell’elemento infinitesimo
– La distanza dell’elemento infinitesimo dall’asse di
rotazione sarà proprio il valore assoluto di x.


L
M
I*  dmR 
ldx x 
L
sbarra
L 2
2
2
2
L
3
3
M x  2 M 
L
L

  1 ML2
x dx     

L  3 L
L 3 8 3 8  12
L 2

L
2 2
3
2
G.M. - Informatica B-Automazione 2002/03
•
•
•
Ciascuna delle tre pale del rotore di un elicottero, mostrate in figura , è lunga
5.20m ed ha una massa di 240 kg
Qual è il momento di inerzia del rotore rispetto all’asse di rotazione? (le pale
possono essere considerate come asticelle sottili)
Qual è l’energia cinetica rotazionale del rotore alla velocità angolare di 350
giri/min?
Applica
zione
1
1
2
2
2
I p ala  ML   240kg  5.20  2163.2kgm
3
3
I ro tore  3Ip ala  3  2163.2kgm 2  6489.6kgm 2

K
350giri 350  2 rad

 36.6 rad
s
min
60s
1 2 1
2
I   6489.6  36.6  4.34MJ
2
2
G.M. - Informatica B-Automazione 2002/03
•
L’elemento oscillante di un pendolo è costituito da una sbarretta di massa
ms=0.5kg e lunga 50 cm a cui è attaccata un disco di massa md=1kg di 20cm
di diametro. Determinare il momento di inerzia rispetto ad un asse
perpendicolare all figura passante per l’estremo superiore della sbarretta.
y
I
Asse di rotazione


dm R 
tutto il corp o
2
dm R 
corp o 1
2

dm R
Applic
azione
2
corp o 2
I  I sbarra  I disco
1
1
2
2
2
I sbarra  ML   0.5  0.5  0.0417kgm
3
3
x
I disco 
*
1
1
2
2
2
MR   1.0  0.1  0.005kgm
2
2
I disco  Idisco  Mh  0.005kgm 1.0kg  .5 .1  0.005kgm  .36kgm  .365kgm
*
2
2
I  0.0417  .365  0.407kgm
2
2
2
2
2
G.M. - Informatica B-Automazione 2002/03
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa M=1.2 kg è appeso
Applicaz
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
ione
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
•
Rv
•
Il moto del disco è un moto di rotazione
attorno ad un asse fisso
Introduciamo un sistema di riferimento
•
•
L’asse di rotazione coincide con l’asse z
L’equazione del moto di rotazione M
•
Il momento di inerzia I (disco omogeneo
rispetto al suo asse)
1
1
2
2
2
I  MR   2.5kg  .20m  .05kgm
2
2
•
Dobbiamo ora calcolare Mz:
x
P
z  I
– Le forze esterne agenti sul disco sono
tensione
MzT  TR
peso
MzP  0
reazione vincolare
MzR v  0
•
L’equazione del moto:
1
2
 TR  MR 
2
G.M. - Informatica B-Automazione 2002/03
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa M=1.2 kg è appeso
Applicaz
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
ione
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
•
Per il corpo di massa m invece:
T  Fg  ma
y
Rv
T  mg  ma y
x
1
 TR  MR2 
2
T  mg  ma y
•
Abbiamo ottenuto due
equazioni con le
incognite T, ay, .
•
•
•
Le equazioni non sono sufficienti.
Ma sappiamo che la corda è inestensibile
quindi c’è una relazione tra ay, .
Ruotiamo il disco di un angolo q in senso
antiorario (q negativo), osserveremo il
corpo di massa m abbassarsi di un tratto y
anch’esso negativo:
y  Rq
•
Dividendo per t, e passando al limite
y
q
R
 v y  R
t
t
P
•
E con una seconda derivazione si ottiene
a y  R
G.M. - Informatica B-Automazione 2002/03
•
•
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa m=1.2 kg è appeso
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
1
Il sistema diventa
 TR  MRa y
2
T  mg  ma y
x
1
O meglio:
 T  Ma y
2
T  mg  ma y
Sostituendo:
1
T   Ma y
2
1
 Ma y  mg  ma y
2
Applicaz
ione
Rv
P
•
1
T   Ma y
2
1

 mg  m  M
a
2  y
mg
1.2  9.81 11.7



 4.77 m 2
1
1
s
m  2M
1.2  2  2.5
2.45
1
T   Ma y   12  2.54.77  5.96N
2
ay 

ay
R

4.77 m
.20m
s2  23.8 rad
s2
G.M. - Informatica B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
•
Noi abbiamo già calcolato l’accelerazione
uniforme del corpo di massa m.
Potremmo risolvere il problema per via
cinematica:
2
2
v  v o  2a y (y  y o )

v  24.771  3.1 m s
•
Applicaz
ione
Rv
x
P
v 3.1 m s
 
15.5 rads
R 0.2m
•
Possiamo anche risolvere il problema con la
conservazione dell’energia:
E  Wnc  WT1  WT2 
0
WR v
0
app . a un punto fermo
•
La forza peso della carrucola non fa
lavoro
G.M. - Informatica B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
E  Wnc  WT1  WT2 
0
WR v
mgh 
Rv
0
app . a un punto fermo
Ei  Ef  K i  Ui  K f  Uf
0  mgh 
Applicaz
ione
x
P
1
1 2
2
mv  I  0
2
2
1 2 11
1 
1
2 2
2
mv 
MR   m  M
v
2
22
2
2 
2
v
2mgh
2  1.2  9.81  1
m2
v 

 9.6 2
1 
1 


s
m M
1.2  2.5


2 
2 
2
m
m2
m   v  3.1 s 15.5 rad
s
v  9.6 2  3.1
R 0.2m
s G.M. - Informatica
s
B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
q 
h
1m

 5rad
R 0.2m

•
P
1
2
2
 2.5  .2  15.5  6.0J
4
Ricordiamo il valore della tensione T
determinato precedentemente (T=5.96N)
WT 
•
Rv
x
1 2 11
2 2
I 
MR  
2
22
K  K f  Ki 
Applicaz
ione
q
q
 M dq   TRdq  TRq  5.96  .2  5  5.96J
0
z
0
Per il teorema delle forze vive:
K  Wrisul tante  WT WP  WR v
0
G.M. - Informatica B-Automazione 2002/03
•
Un cilindro di massa 2 kg può ruotare attorno al proprio asse (longitudinale)
passante per O. Nel piano della sezione rappresentata nella figura sono
applicate quattro forze, aventi le intensità F e le distanze r dal centro riportate
in tabella. Trovare l’intensità e il verso dell’accelerazione angolare del
cilindro, ammettendo che, durante il moto, le forze mantengano la
orientazione rispetto al cilindro.
Applicaz
ione
F1  6.0N F2  4.0N F3  2.0N F4  5.0N
R1  5.0cm R 2  12.0cm
M z  I
•
L’equazione del moto:
I
1
1
2
2
2
MR  2kg.12m  0.0144kgm
2
2
F1
M z1  F1R 2  6N  .12m  0.72Nm
F2
M z2  F2 R2  4N  .12m  0.48Nm
F3
M z3  F3R1  2N  .05m  0.10Nm
F4
M z4  0
Mz  .72  0.48  0.10  .14Nm

Mz
.14Nm
rad


9.7
2
2
I
0.0144kgm
s
•
L’accelerazione è diretta in verso
antiorario
G.M. - Informatica B-Automazione 2002/03
•
Una riga di lunghezza L=1m, è messa in posizione verticale, appoggiata al
pavimento e quindi lasciata cadere. Trovate la velocità dell’estremità superiore
quando colpisce il pavimento, ammettendo che l’estremità inferiore non slitti
•
•
•
•
Applicaz
ione
Possiamo considerare la riga come una sbarretta sottile.
Il moto di caduta può essere immaginato come un moto di
rotazione attorno ad un asse passante per il punto di contatto
O.
Le forze agenti sono la forza peso, la normale e la forza di
attrito (statico) che mantiene fermo il punto di contatto.
Possiamo applicare la conservazione dell’energia:
E  Wn c 
WN  WFa
0
0
p erch è ap pl. p un to fermo
Ei  Ef  K i  Ui  K f  Uf
U=0
L 1 2
0  mg  I  0
2 2
L
2
2  mgL  3g
 
1
1
I
mL 2 L
2
3
P
mg
 
3g
L
N
Fa O
3g
m
v  L 
L  3gL  5.42
L
s
G.M. - Informatica B-Automazione 2002/03
•
Un corpo rigido è formato da tre asticelle sottili identiche di lunghezza L, unite
tra loro in modo da assumere una forma ad H come mostrato in figura.
L’insieme è libero di ruotare intorno ad una asse orizzontale fosso che coincide Applicaz
con una delle gambe della H. Partendo da una posizione di riposo in cui il
ione
piano della H è orizzontale, il sistema è lasciato libero di cadere.
Qual è la velocità angolare del corpo quando il piano della H arriva in
posizione verticale?
•
•
•
Rv
Proviamo ad applicare la conservazione
dell’energia
Le forze agenti sono il Peso e la reazione
vincolare applicata dall’asse di rotazione:
E  Wn c 
P
0
WR v
0
p erch è ap pl. p un to fermo
Asse di rotazione
Ei  Ef  K i  Ui  K f  Uf
0  MgL 
2 
1 2
L
I  Mg
2
2
L
2  MgL
1
I
I
2
Mg
M  3m
•
U=0
Dobbiamo calcolare il momento di inerzia
dell’H rispetto all’asse di rotazione
G.M. - Informatica B-Automazione 2002/03
•
•
Un corpo rigido è formato da tre asticelle sottili identiche di lunghezza L, unite
tra loro in modo da assumere una forma ad H come mostrato in figura.
L’insieme è libero di ruotare intorno ad una asse orizzontale fosso che coincide Applicaz
con una delle gambe della H. Partendo da una posizione di riposo in cui il
ione
piano della H è orizzontale, il sistema è lasciato libero di cadere.
Qual è la velocità angolare del corpo quando il piano della H arriva in
posizione verticale?
I  I1  I 2  I3
I
•
I1  0
1 2
I 2  mL
3
2
I 3  0  mL
I1
1
4
2
2
2
mL  mL  mL
3
3
I3
La velocità angolare vale dunque:

I2
 
2
MgL 3mgL
9g


4 2 4L
I
mL
3
9g
4L
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
Una forza orizzontale costante di 10 N è applicata a una ruota di massa
M=10kg e raggio R=0.30 m, nel modo come indicato in figura. La ruota rotola
senza strisciare sulla superficie orizzontale, e l’accelerazione del suo centro di
massa è 0.60 m/s2.
Quali sono l’intensità ed il verso della forza di attrito sulla ruota
Qual è il momento di inerzia della ruota intorno all’asse di rotazione passante
per il suo centro?
Applic
azione
Dal teorema del centro di massa: F  P  N  Fas  Ma CM
N
x F  Fas  Ma CM x
y N  Mg  Ma CM y  0
y
N  Mg
x
Fas  F  Ma CMx  10 10  .60  4N
•
per la rotazione
Mz  I 
*
*
F
Mz  0
P
Mz  0
N
Mz  0
Fas M z  FasR
F
I 
*
Fas
1
2
MR
2
Fas R  I 
R 2 Fas .32  4 .36
I 


 0.6kgm 2
a CM x
0.60
0.60
*
P
ax  R
Fas  I
*
a CM x
2
R
*
G.M. - Informatica B-Automazione 2002/03
•
Una forza orizzontale costante di 10 N è applicata a un cilindro di massa
M=10kg e raggio R=0.20 m, attraverso una corda avvolta sul cilindro nel modo
come indicato in figura. Il cilindro rotola senza strisciare sulla superficie
orizzontale. Determinare:
l’accelerazione del suo centro di massa.
L’intensità ed il verso della forza di attrito necessario per assicurare il moto di
puro rotolamento
Il minimo coefficiente di attrito tra il cilindro e il piano orizzontale .
•
•
•
•
y
Supponiamo che la forza di attrito statico sia diretta in
verso opposto alla forza applicata F, salvo ricrederci se
risolvendo il problema ci risultasse un modulo negativo.
•
•
Applic
azione
N
Dal teorema del centro di massa: F  P  N  Fas  Ma CM
x F  Fas  Ma CM x
N  Mg
y N  Mg  Ma CM y  0
x
Fas
F
P
La rotazione attorno al centro di massa: M z  I 
*
F
M z  FR
P
Mz  0
N
Mz  0
Fas M z  FasR
I 
*
1
2
MR
2
FR  FasR  I 
*
*
Traslazione
F  Fas  Ma CM x
Rotazione
 FR  FasR  I 
con dizion e di p uro ro tolamento
a CM x  R
*
G.M. - Informatica B-Automazione 2002/03
•
Una forza orizzontale costante di 10 N è applicata a un cilindro di massa
M=2kg e raggio R=0.20 m, attraverso una corda avvolta sul cilindro nel modo
come indicato in figura. Il cilindro rotola senza strisciare sulla superficie
orizzontale. Determinare:
l’accelerazione del suo centro di massa.
L’intensità ed il verso della forza di attrito necessario per assicurare il moto di
puro rotolamento
Il minimo coefficiente di attrito tra il cilindro e il piano orizzontale .
•
•
•
•
Traslazione
F  Fas  Ma CM x
Rotazione
 FR  FasR  I 
con dizion e di p uro ro tolamento
a CM x  R
Applic
azione
y
N
*
x
P
F
Fas
Ricavando la forza di attrito statico dalla prima e sostituendo:
2FR
2FR
2F
Fas  F  MR
 *





2
3
1 MR2  MR2
I

MR
MR
2
*
2
2
 FR  FR  MR   I 
2FR
 *
2
I  MR
4F
4  10

 33.3 rad
s2
3MR
3  2  0.2
aCMx  R  0.2  33.3  6.66 m2
s
• Il fatto di aver trovato il modulo
Fas  F  MR  10  2  0.233.3  3.32N
della forza di attrito negativa, vuol
dire che la nostra ipotesi iniziale
Fas Fas
3.32
Fas  s N  s 


 .17
circa il verso della Fas era sbagliato.
N Mg 2  9.81
G.M. - Informatica B-Automazione 2002/03

•
•
•
•
•
•
Un cilindro pieno di raggio 10 cm e massa 12 Kg, partendo da fermo, rotola
senza strisciare per una distanza di 6 m giù per il tetto di una casa inclinato di di
30 °
Quando lascia il bordo del tetto, qual è la sua velocità angolare rispetto ad un
asse passante per il suo centro di massa
La parete esterna della casa è alta 5 m, a che distanza dal bordo del tetto
atterrerà sul terreno piano?
Consideriamo dapprima il moto di puro rotolamento sul
tetto
Le forze agenti sono la forza peso, la Normale, la forza
di attrito statico.
Possiamo trovare la velocità finale utilizzando la
conservazione dell’energia meccanica totale
E  Wn c 
WN  WFa
Applic
azione
i
L
U=0
f
0
0
p erch è ap pl. p un to fermo
Ei  Ef  K i  Ui  K f  Uf
Kf

p er il teo rema di Ko nig
Kf 
1
1
1 * 2
2
*
2
MvCM  K  MvCM  I 
2
2
2
G.M. - Informatica B-Automazione 2002/03
•
•
•
Un cilindro pieno di raggio 10 cm e massa 12 Kg, partendo da fermo, rotola
senza strisciare per una distanza di 6 m giù per il tetto di una casa inclinato di di
30 °
Quando lascia il bordo del tetto, qual è la sua velocità angolare rispetto ad un
asse passante per il suo centro di massa
La parete esterna della casa è alta 5 m, a che distanza dal bordo del tetto
atterrerà sul terreno piano?
Ki  U i  Kf  U f
0  MgL sen 30 
•
La condizione di puro rotolamento:
vCM  R 
•
1
1
Mv 2CM  I* 2  0
2
2
Applic
azione
i
L
U=0
f
v 2CM  R 2 2
Il momento di inerzia del Cilindro:
I 
*
1
2
MR
2
1
11
2 2
2 2
MgL sen30  MR  
MR 
2
22

4gL sen 30

3R2
4  9.81 6  0.5
rad
 3924  62.6
3  .12
s
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
•
Un cilindro pieno di raggio 10 cm e massa 12 Kg, partendo da fermo, rotola
senza strisciare per una distanza di 6 m giù per il tetto di una casa inclinato di di
30 °
Quando lascia il bordo del tetto, qual è la sua velocità angolare rispetto ad un
asse passante per il suo centro di massa
La parete esterna della casa è alta 5 m, a che distanza dal bordo del tetto
atterrerà sul terreno piano?
Affrontiamo ora la seconda parte del problema.
Dobbiamo innanzitutto calcolarci il modulo della
velocità del CM
– Usiamo la condizione di puro rotolamento:
Applic
azione
y
v
m
s
La velocità è diretta come mostrato in figura.
v CM  R  0.1  62.6  6.26
•
•
•
Quando il cilindro abbandona il tetto, il moto del suo
centro di massa è come il moto del proiettile.
Facendo ripartire l’orologio al momento del distacco,le
condizioni iniziali sono:
x o  0m v x o  6.26cos 30  5.42 ms
yo  5m v y o  6.26sen 30 
3.13 ms
x
x  v xot
y  y o  vyo t  12 gt 2
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
Un cilindro pieno di raggio 10 cm e massa 12 Kg, partendo da fermo, rotola
senza strisciare per una distanza di 6 m giù per il tetto di una casa inclinato di di
30 °
Quando lascia il bordo del tetto, qual è la sua velocità angolare rispetto ad un
asse passante per il suo centro di massa
La parete esterna della casa è alta 5 m, a che distanza dal bordo del tetto
atterrerà sul terreno piano?
y
Determiniamo l’istante di impatto al suolo imponendo
che y sia nulla:
y o  vy ot  12 gt 2  0  4.9 t 2  3.13t  5  0
t 1, 2
•
•
v
b  b 2  4ac 3.13  3.132  4  4.91  5 3.13 10.39 1.37




0.74
2a
9.81
9.81
La soluzione negativa è da scartare.
La distanza a cui atterrerà:
x  v x ot  5.42  .74  4.01m
•
Applic
azione
d  xf  x o  4.01m
x
Si osservi che la velocità di rotazione attorno all’asse passante per il centro
di massa rimane costante dal momento del distacco fino all’impatto al
suolo.
– L’unica forza esterna agente, la forza peso, essendo applicata al CM, ha
momento assiale nullo rispetto all’asse di rotazione.
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
•
Un corpo di massa m e raggio R rotola senza strisciare a velocità v su un piano
orizzontale. Prosegue rotolando su per una rampa fini ad una altezza massima h
Se h=3v2/(4g), qual è il momento di inerzia del corpo rispetto all’asse passante
per il centro di massa?
Di che tipo di corpo si tratta?
Applic
azione
Le forze agenti sono: il peso, la normale e la forza di
attrito.
Possiamo applicare la conservazione dell’energia
v
Ki  U i  Kf  U f
h
1
1
Mv2  I* 2  0  0  mgh
2
2
•
2
2
v
3v
1
1
mv 2  I* 2  mg
2
2 R
4g
Da cui:
I m
*
•
m  I*
1
3

m
R2
2
3  2 1
2
 1 R  mR
2 
2
Si tratta di un cilindro
G.M. - Informatica B-Automazione 2002/03
•
•
•
•
Nella figura vediamo una scala dei pompieri di lunghezza L=12 m e massa
m=45 kg appoggiata con l’estremità superiore ad un muro privo di attrito, ad
una altezza h=9.3 m dal suolo. Il suo centro di massa si trova a un terzo della
sua lunghezza. Un vigile del fuoco con massa M=72 kg si arrampica per la
scala fino a che il suo centro di massa si trova a metà della scala.
Quali forze esercitano, in modulo il muro ed il terreno?
Applic
azione
In problemi di questo tipo tutte le forze sono
contenute nel piano del disegno
Il problema diventa un problema piano con
solo tre gradi di libertà
– Moto lungo l’asse x
– Moto lungo l’asse y
– Rotazione attorno all’asse z
•
Le condizioni di equilibrio si trovano
imponendo che
– La componente x della risultante delle forze
sia nulla
– La componente y della risultante delle forze
sia nulla
– Il momento assiale Mz sia nullo
Si osservi che scegliendo un polo sul piano che contiene le forze, i rispettivi
momenti hanno solo la componente z.
G.M. - Informatica B-Automazione 2002/03
•
•
Nella figura vediamo una scala dei pompieri di lunghezza L=12 m e massa
m=45 kg appoggiata con l’estremità superiore ad un muro privo di attrito, ad
una altezza h=9.3 m dal suolo. Il suo centro di massa si trova a un terzo della
sua lunghezza. Un vigile del fuoco con massa M=72 kg si arrampica per la
scala fino a che il suo centro di massa si trova a metà della scala.
Quali forze esercitano, in modulo il muro ed il terreno?
Rx  0
Applic
azione
Fm  Ftx  0
Ry  0
 Mg  mg  Fty  0
a
a
M z  0  Fm h  Mg  mg  0
2
3
•
NB: per il calcolo di Mz si può scegliere un
punto qualsiasi del piano.
– Scegliendo il punto O ci siamo evitato di
calcolare due momenti quello di Ftx e quello di
Fty
a  L  h  12  9.3  7.58m
2
Fm 
Mg
2
2
2
a
a
7.58
7.58
 mg
72  9.81
 45  9.81 
2
3
2
3  407.8N
h
9.3
Ftx  Fm  407.8N
Fty  Mg  mg  1147.8N
•
NB: non ci può essere equilibrio
senza
sul pavimento
G.M. -attrito
Informatica
B-Automazione 2002/03
•
Nella situazione della figura, qual è l’intensità minima della forza orizzontale F
da applicare al mozzo della ruota per superare un ostacolo di altezza h? Sia r il
raggio della ruota ed m la sua massa.
•
Applic
azione
Se aumentiamo la forza F da zero fino a quando
la ruota non supera l’ostacolo
– Quando la forza applicata è piccola la situazione
della altre forze agenti è quella illustrata nella
figura accanto
•
Un attimo prima che la ruota si mette in
movimento la situazione è quella illustrata nella
figura in basso
P
Rv
N
– La normale N è diventata nulla (perdita di
contatto)
•
Equilibrando i momenti rispetto allo spigolo
Fr  h   mg r  r  h  0
2
2
mg r 2  r 2  h2  2rh mg h2r  h
F

r  h 
r  h
P
Rv
G.M. - Informatica B-Automazione 2002/03
•
Un disco di grammofono di raggio r=0.10 m gira intorno ad un asse centrale
verticale alla velocità di 4.7 rad/s. Il suo momento di inerzia rispetto all’asse di
rotazione vale 5.0x10-4 kgm2. Un pezzetto di stucco di massa 0.020 kg cade
dall’alto verticalmente sul disco e si appiccica sul bordo.
Qual è la velocità angolare del disco subito dopo che lo stucco si è attaccato?
•
•
•
•
•
•
•
Applic
azione
L’urto è un urto anelastico, dopo l’urto i due oggetti si muovono
z
restando attaccati

Le forze esterne presenti sono le forze peso del disco e dello stucco
più la reazione vincolare esercitata dall’asse di rotazione
v
Proprio la presenza della reazione vincolare non consente la
O
conservazione della quantità di moto
Poiché la reazione vincolare, impulsiva, è applicata all’asse di
rotazione, ha momento assiale nullo rispetto all’asse di rotazione.
Anche le altre forze esterne presenti, le forze peso, essendo verticali
hanno momento assiale nullo rispetto all’asse di rotazione
Lzi  Lzf
Quindi si conserva il momento angolare assiale Lz.
L zi  L zidisco  L zistucco  I disco  5.0  104  4.7  23.5  10 4 kgm 2s1
0 v p arallela a z
L zf  L zf discostucco  I disco  Istucco  f
L zf  L zi
 f 
L zi
L zi

I disco  Istucco  Idisco  m stuccor 2


L zi
23.5  10 4
23.5  10 4
rad
f 



3.36
4
I disco  mstuccor 2
5  104  .020  .10 2
7  10
s
G.M. - Informatica
B-Automazione 2002/03

 

•
•
Una palla di acciaio di massa m 0.515 kg è attacca ad una sbarra, di massa pari
a 0.515 kg e lunghezza L=70 cm, il cui altro estremo è incernierato ad un asse
orizzontale passante per il punto O. Il sistema composto dalla palla e dalla
sbarra può ruotare liberamente attorno all'asse orizzontale passante per O. La
palla viene lasciata libera quando la sbarra è orizzontale. Come mostrato in
figura nel punto più basso della sua traiettoria la palla colpisce un blocco di
acciaio di 2.50 kg stazionario su un piano privo di attrito. L'urto è elastico.
y
Trovare
Applic
azione
O
– la velocità della palla e la velocità del blocco subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di rotazione sulla sbarra
subito prima e subito dopo l'urto.
•
La densità dell'acciaio è 7.87 g/cm3. Il momento di inerzia di
una sfera omogenea rispetto ad un suo diametro è 2/5 mr2
x
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
y
O
Si possono distinguere varie fasi
– Caduta dalla posizione orizzontale iniziale alla posizione verticale
– Urto con il blocco
– Fase successiva all’urto (palla che riparte dalla posizione verticale
e ruota attorno all’asse di rotazione, blocco che si allontana dalla
posizione che aveva prima dell’urto.
•
Applic
azione
U=0
U i_ p alla  m p allag(L  r)
x
Lo studio della prima fase ci permette di determinare la velocità
U i_ sbarra  m sbarrag(L  r)
angolare della sbarra+palla prima dell’urto
– Durante il moto di caduta agisce la forza peso e la reazione
vincolare
– Possiamo applicare la conservazione dell’energia
E  Wnc 
WR v
0
0
perchè ap pl. pun to fermo
Ei  Ef  K i  Ui  K f  Uf
Ei  Ef
•
U f _ p alla  0
L
U f _ sbarra  m sbarrag(  r)
2
Ki  0
Dobbiamo calcolarci il raggio
1
della palla e il momento di
K f  I 2f
inerzia I complessivo rispetto
2
all’asse di rotazione
 K i  Ui _ p alla  Ui _ sbarra  K f  Uf _ pG.M.
Uf _ sbarraB-Automazione 2002/03
- Informatica
alla 
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
y
Applic
azione
O
Il raggio della palla
3mp alla
4 3
m p alla  rV  r r  r  3
3
4r
g
10 3 kg
3 kg
r  7.87 3  7.87

7.87

10
3
3
2
cm
m
10 m

r 3
3m palla
4r
3
x

3  .515
3  0.025m
4  3.14  7.87 10
I  I p alla  Isbarra
I p alla 
U=0
2
m p alla r 2  m p alla L  r 2  .270kgm 2
5
I  I p alla  Isbarra 
 .270  0.084  0.354kgm 2
stein er
1
1
I sbarra  m sbarraL2   0.515  .72  0.084kgm 2
3
3
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
applichiamo la conservazione dell’energia:
K i  Ui _ p alla  Ui _ sbarra  K f  Uf _ p alla  Uf _ sbarra
y
Applic
azione
O
U=0
x
1 2
L 
I f  0  msbarrag
r

2
2 
L

L
m p alla gL  r   msbarrag L  r   r m p allagL  r  m sbarrag 

2 
2
2 
f 

1
1
I
I
2
2
0.7 
0.515  9.81  0.7  0.025  0.515  9.81
 2 
rad 2   19.1 rad
2
f
f 
 364.8 2
s
1
s
 0.354
2
0  m p allagL  r   m sbarragL  r  
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
•
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
y
 =19.1rad/s
Abbiamo determinato la velocità angolare della sbarra immediatamente
prima dell’urto
Possiamo passare alla soluzione della seconda fase, l’urto vero e proprio.
Le forze esterne agenti sul sistema rigido sbarra-palla e sul blocco,
l’insieme dei corpi che si urtano, sono:
–
–
–
•
Trovare
Applic
azione
O
x
Le forze peso
La reazione vincolare applicata dall’asse di rotazione al corpo rigido sbarra-palla
La normale N esercitata dal piano orizzontale sul blocco
Sia la reazione vincolare che la normale N possono diventare impulsive
durante l’urto
–
–
–
–
Dalla figura si vede che la forza interna che agisce sul blocco è orizzontale
non influenza quello che avviene nella direzione verticale:
Poiché la normale N necessariamente deve essere verticale,
la normale N non è impulsiva
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
 =19.1rad/s
y
Applic
azione
O
Per quanto riguarda la reazione vincolare invece
– L’unico vincolo che possiamo porre alla sua direzione è che
deve esser perpendicolare al vincolo (all’asse di rotazione)
– Quindi può benissimo avere delle componenti orizzontali
•
•
•
•
x
La reazione vincolare può avere un comportamento impulsivo
Non possiamo applicare la conservazione della quantità di
L zi sbarrapall a  I
moto
L zi blocco  0
Osserviamo che il momento assiale della reazione vincolare è
L zf sbarrapall a  I'
nullo (il braccio è nullo)
L zf blocco  L  rm bloccov'
Allora si conserva il momento angolare assiale!!
L zi  L zf
L zisbarra p alla  L ziblo cco  L zf sbarrap alla  L zf blo cco
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
Applic
azione
y
 =19.1rad/s
Calcolo del momento angolare assiale del blocco dopo l’urto:
L  r  mv
•
•
•
L  rmv senq  mv rsen q  mv(L  rp )
x
La direzione è perpendicolare al piano del disegno
Il verso è quello dell’asse z
La componente assiale è proprio uguale al modulo del
momento
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
 =19.1rad/s
y
Abbiamo potuto affermare che nell’urto si conserva il
momento angolare assiale:
L zi  L zf
L zisbarra p alla  L ziblo cco  L zf sbarrap alla  L zf blo cco
L zi sbarrapall a  I
L zi blocco  0
L zf sbarrapall a  I'
Applic
azione
O
x
I  0  I' m blo ccov' L  r
L zf blocco  L  rm bloccov'
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
 =19.1rad/s
y
Poiché sappiamo che l’urto è elastico, allora nell’urto si
conserva anche l’energia cinetica.
K i  Kf
O
x
Kisbarrap alla  Kiblo cco  K f sbarrap alla  Kf blo cco
K zisbarra p alla 
1 2
I
2
K ziblo cco  0
K zfsbarra p alla 
K zfblo cco
Applic
azione
1
I' 2
2
1 2
1
1
2
2
I  0  I'  m bloccov'
2
2
2
1
 m blo ccov' 2
2
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Ricapitolando
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
y
 =19.1rad/s
Applic
azione
O
I  I'  m blo ccov' L  r 
1 2 1
1
2
2
I  I'  m bloccov'
2
2
2
•
•
•
•
x
Abbiamo due equazioni in due incognite, v’ e w’.
Non abbiamo bisogno di altre equazioni per trovare la soluzione
Conviene comunque eliminare i quadrati dalla seconda equazione
Riscriviamo il sistema nella seguente forma:
I  '   m blo ccov' L  r •


I  2  ' 2  m blo ccov' 2
Dividendo la seconda per la prima:
I  '   m blo ccov' L  r
  ' 
v'
Lr
v'  L  r  ' 
•
Sostituendo
nella prima
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
I  '   m blo ccov' L  r
v'  L  r  ' 
I  m
•
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
y
 =19.1rad/s
Applic
azione
O
Sostituendo
I '   mblocco   ' L  r
2
x
2
2

L

r



I

m

L

r



'
blo cco
blo cco
I  m blocco L  r 
0.354  2.5  .725
rad
'  
2  19.1
2  11.0
I  m blocco L  r 
0.354  2.5  .725
s
2
•
2
Il fatto che ’ sia negativa significa che nell’urto il corpo rigido sbarrapalla inverte il moto e torna indietro.
v'  L  r  '   .725  19.1  11.0  5.9
m
s
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
y
 =19.1rad/s
Infine valutiamo il valore della reazione vincolare subito prima
(e poi subito dopo) l’urto.
Subito prima dell’urto la situazione è quella mostrata in figura
L’equazione che contiene la reazione vincolare è il teorema del
centro di massa applicato al corpo rigido sbarra-palla
•
•

Applic
azione
O
x

P  R v  msbarra  mpalla a CM
•
•
•
Poiché il peso è noto se noi conoscessimo l’accelerazione del
centro di massa potremmo determinare la reazione vincolare
Il centro di massa della sbarra si muove su una traiettoria
circolare con centro sull’asse di rotazione
Sarà soggetto ad una accelerazione centripeta e una
accelerazione tangenziale
a CM c   2rcm
a CM t  rcm
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2

Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
 =19.1rad/s
–
O
x
a CM c   rcm

a CM t  rcm
Noi abbiamo già calcolato  nella posizione desiderata
 invece la possiamo calcolare attraverso l’equazione del moto
di rotazione attorno ad un asse fisso
I  Mz
•
•
•
y
2
P  R v  msbarra  mpalla a CM
•
Applic
azione
Dobbiamo calcolarci rCM la distanza del CM dall’asse di
rotazione.
Calcoliamoci yCM ponendo l’origine dell’asse y proprio in
corrispondenza dell’asse di rotazione
y cm 
msbarra yCM _ sbarra  m pallay CM _ palla
m sbarra  m palla
rcm  0.54m

Osserviamo che nella
posizione considerata 
è nulla perché Mz è nullo
.515  .35  .515  .725
.35  .725

 0.54m
.515  .515
2
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2

Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
 =19.1rad/s
•
y

x
a CM t  rcm
Osserviamo che nella posizione considerata  è nulla
perché Mz è nullo
Proiettando sugli assi x e y
x
O
a CM c   rcm

rcm  0.54m
y
2
P  R v  msbarra  mpalla a CM
I  Mz
Applic
azione


g  m

 r
R v x  msbarra  m p alla a CM t  m sbarra  m p alla rcm  0

Rv y  m sbarra  m p alla
sbarra
 m p alla
2
cm
.515  .51519.12  0.54  9.81 213N
prima
R vy  m sbarra  m palla  rcm  g
.515  .51511.0 2  0.54  9.81 131.9N dopo
2
G.M. - Informatica B-Automazione 2002/03
–
–
–
–
–
–
–
–
•
•
mpalla =0.515 kg
•
msbarra =0.515 kg
mblocco =2.50 kg
L=70 cm
Densità acciaio= 7.87 g/cm3
Isfera= 2/5 mr2
R=0.025 m
I=0.354kgm2
Trovare
– la velocità della palla e la velocità del blocco
subito dopo l'urto.
– La reazione vincolare esercitata dall'asse di
rotazione sulla sbarra subito prima e subito dopo
l'urto.
–
 =19.1rad/s
Applic
azione
y
O
x
Possiamo concluder questo esercizio valutando l’impulso della
reazione vincolare durante l’urto
Dalla definizione di impulso sappiamo che
I  Psist  Pf _sist  Pi _sist
Pi_ sist  Pi _ sbarra_ p alla  Pi_ blo cco

0

Pi_sbarra _ palla  msbarra  mpalla v i_CM 


 msbarra  mpalla i rCM i
Pf _sist  Pf _sbarra_ palla  Pf _ blocco


Pf _sbarra _ palla  msbarra  mpalla v f _CM


 msbarra  mpalla f rCM i
Pf _ blo cco  mblo cco vf _ blo cco 
Pf _ blo cco  mblo cco v' i
G.M. - Informatica B-Automazione 2002/03
•
•
Un tondino di acciaio da costruzione ha raggio R=9.5 mm e lunghezza L =81
cm. Una forza di modulo 6.2 x104 lo tira longitudinalmente. Qual è lo sforzo
nel tondino?
Quanto l’allungamento e la sua deformazione?
•
La sezione del tondino è data da:

A  R  3.14  9.5  10
2
•
Lo sforzo:
•
La deformazione:
•
L’allungamento:

3 2
6
 283  10 m
Applic
azione
2
F
6.2  104
8 N
 

2.19

10
6
2
A 283  10
m
L  2.19  108
 
9  0.0011
L
E 200  10

2.19  10 8
L  L 
9  0.81  0.0011 0.81  0.00089m  0.9mm
E
200  10
G.M. - Informatica B-Automazione 2002/03
•
A che profondità bisogna immergersi in mare perché la pressione raddoppi
rispetto a quella in superficie
•
Dalla legge di Stevino ricaviamo che la pressione alla profondità
h in un liquido conoscendo quella in superficie Po, è data da:
Applic
azione
P  Po rgh
•
Vogliamo trovare h* in modo che P sia uguale a
2Po.
P
*
*
2Po  Po  rgh  h  o
rg
P
1atm
*
• Da cui:
h  o 

kg
rg 1.024  103 3 9.81 m2
m
h
s
1.01  10 Pa

 10.05m
3 kg
1.024  10 3 9.81 m2
5
m
•
•
Ogni 10 m di profondità la pressione aumenta di un atmosfera
Se al posto dell’acqua c’è un gas,
–
•
•
s
la densità del gas è circa 1000 volte più piccola di quella dell’acqua
Alla profondità di 10 m in un gas la pressione sarebbe cambiata solo di 1
millesimo di atmosfera
Per recipienti di piccolo volume, entro i 10 m di profondità, possiamo
considerare la pressione costante in tutto il recipiente.
P  Po  rgh
se rh  0
P  Po  cos2002/03
tan te
G.M. - Informatica B-Automazione